3.1 圆 课件(共31张PPT)
图片预览











文档简介
(共31张PPT)
3.1 圆
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆
1. 圆的定义
(1)描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周, 另一个端点A 所形成的图形叫做圆.其固定的端点O 叫做圆心,线段OA 叫做半径.
(2)集合观点定义:圆可以看成是所有到定点(圆心O)的距离等于定长(半径r)的点的集合.
知1-讲
感悟新知
特别提醒
1. 确定一个圆需要“两个要素”,一是圆心,圆心定其位置;二是半径,半径定其大小.
2. 圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
知1-讲
感悟新知
2. 圆的表示法 以点O 为圆心的圆,记作⊙ O,读作“圆O”.
3. 圆的特性 (1)同圆的半径相等.
(2)到圆心的距离等于半径的点在圆上.
感悟新知
知1-练
下列说法中, 错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例 1
感悟新知
知1-练
1-1. 下列条件中,能确定唯一一个圆的是( )
A. 以点O 为圆心
B. 以2 cm 长为半径
C. 以点O 为圆心,5 cm长为半径
D. 半径为2 cm 且经过点A
C
感悟新知
知1-练
1-2. 到点O 的距离等于8 cm 的点的集合是以点________为圆心,以________ cm长为半径的圆.
O
8
感悟新知
知1-练
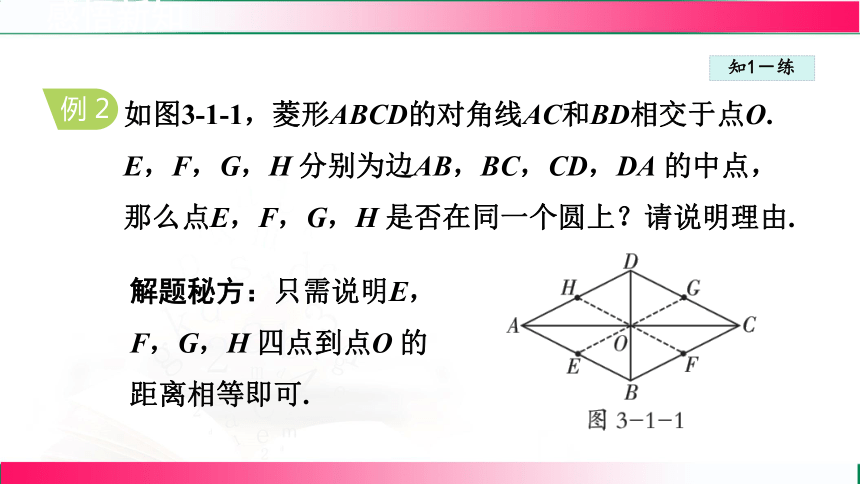
如图3-1-1,菱形ABCD的对角线AC和BD相交于点O.
E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例 2
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等即可.
感悟新知
知1-练
解:点E,F,G,H 在同一个圆上,理由如下:
如图3-1-1,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,
AC ⊥ BD.
感悟新知
知1-练
又∵ E 为AB 边的中点,∴ OE=AB.
同理可得,OF=BC,OG=CD,OH=DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
知识点
圆的有关概念
知2-讲
感悟新知
2
定义 注意
弦 连接圆上任意两点的线段叫做弦 圆中有无数条弦,其中直径是最长的弦
直径 经过圆心的弦叫做直径
知2-讲
感悟新知
弧、半圆、劣弧、优弧、 (1)圆上任意两点间的部分叫做圆弧,简称弧;(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;(3)小于半圆的弧叫做劣弧;(4)大于半圆的弧叫做优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
续表
知2-讲
感悟新知
等圆 能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 在同圆或等圆中,能够互相重合的弧叫做等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
前提
续表
知2-讲
感悟新知
特别提醒
1. 弦与直径的关系:直径是圆中最长的弦,但弦不一定是直径.
2. 弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦和弧都有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条.
感悟新知
知2-练
下列语句中:①直径是弦;②弦是直径;③半径相等
的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有 ____________.
①③⑤
例 3
知2-练
感悟新知
3-1. 如图,在⊙ O 中,点A,O,D 在一条直线上, 点B,O,C 在一条直线上,那么图中有________条弦.
3
知识点
点和圆的位置关系
知3-讲
感悟新知
3
点和圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等级关系
点在圆外 点到圆心的距离大于半径
点在圆上 点到圆心的距离等于半径
点在圆内 点到圆心的距离小于半径
知3-讲
感悟新知
特别提醒
符号“ ”读作“等价于”,它表示符号“ ”左右两端互为因果关系.
感悟新知
知3-练
如图3-1-2,已知⊙ O 的半径r=5 cm,圆心O 到直线l 的距离d=OD=3 cm,在直线l 上有P,Q,R 三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的?
例 4
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
知3-练
感悟新知
解:如图3-1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP=5 cm=r. ∴点P 在⊙ O 上.
∵ QD=5 cm,∴ OQ= cm>5 cm,∴点Q 在⊙ O 外.
∵ RD=3 cm,∴ OR=3 cm<5 cm. ∴点R 在⊙ O 内.
知3-练
感悟新知
4-1. 在矩形ABCD 中,AB=8,AD=6,以顶点D 为圆心作半径为r 的圆,若要求另外三个顶点A,B,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是 ________.
6返回
1. 有下列说法:①同圆中,所有的半径都相等;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆. 其中正确的说法有( )
A. 1个 B. 2个
C. 3个 D. 4个
C
返回
D
返回
3. 如图,点A,D,G,M在半圆O上,四边形ABOC,四边形DEOF,四边形HMNO均为矩形,设BC=a,EF=b,NH=c,则下列选项正确的是( )
A. a>b>c
B. a=b=c
C. c>a>b
D. b>c>a
B
返回
4. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法中不正确的是( )
A. 当a<5时,点B在⊙A内
B. 当1<a<5时,点B在⊙A内
C. 当a<1时,点B在⊙A外
D. 当a>5时,点B在⊙A外
A
返回
5. [教材P66随堂练习T2]如图是某同学在体育课上投掷四次铅球的成绩示意图,该同学投掷铅球最好成绩的点为________. (填C,D,E,F中的一个字母)
F
返回
6. 在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,并判断A,B两点和⊙C的位置关系.
【解】如图.∵∠C=90°,AC=4,
AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=r,∴点B在⊙C上.
返回
7. 在平面直角坐标系中,已知⊙O的圆心与原点重合,半径为5,则下列各点中,不在圆上的点是( )
A. (4,3) B. (1,-4)
C. (-3,4) D. (-5,0)
B
课堂小结
圆
圆
弦、弧、等圆、等弧
两要素
位置
大小
圆心
半径
相关概念
点与圆的位置关系
点在圆上、圆内、圆外
谢谢观看!
3.1 圆
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆
1. 圆的定义
(1)描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周, 另一个端点A 所形成的图形叫做圆.其固定的端点O 叫做圆心,线段OA 叫做半径.
(2)集合观点定义:圆可以看成是所有到定点(圆心O)的距离等于定长(半径r)的点的集合.
知1-讲
感悟新知
特别提醒
1. 确定一个圆需要“两个要素”,一是圆心,圆心定其位置;二是半径,半径定其大小.
2. 圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
知1-讲
感悟新知
2. 圆的表示法 以点O 为圆心的圆,记作⊙ O,读作“圆O”.
3. 圆的特性 (1)同圆的半径相等.
(2)到圆心的距离等于半径的点在圆上.
感悟新知
知1-练
下列说法中, 错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例 1
感悟新知
知1-练
1-1. 下列条件中,能确定唯一一个圆的是( )
A. 以点O 为圆心
B. 以2 cm 长为半径
C. 以点O 为圆心,5 cm长为半径
D. 半径为2 cm 且经过点A
C
感悟新知
知1-练
1-2. 到点O 的距离等于8 cm 的点的集合是以点________为圆心,以________ cm长为半径的圆.
O
8
感悟新知
知1-练
如图3-1-1,菱形ABCD的对角线AC和BD相交于点O.
E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例 2
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等即可.
感悟新知
知1-练
解:点E,F,G,H 在同一个圆上,理由如下:
如图3-1-1,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,
AC ⊥ BD.
感悟新知
知1-练
又∵ E 为AB 边的中点,∴ OE=AB.
同理可得,OF=BC,OG=CD,OH=DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
知识点
圆的有关概念
知2-讲
感悟新知
2
定义 注意
弦 连接圆上任意两点的线段叫做弦 圆中有无数条弦,其中直径是最长的弦
直径 经过圆心的弦叫做直径
知2-讲
感悟新知
弧、半圆、劣弧、优弧、 (1)圆上任意两点间的部分叫做圆弧,简称弧;(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;(3)小于半圆的弧叫做劣弧;(4)大于半圆的弧叫做优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
续表
知2-讲
感悟新知
等圆 能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 在同圆或等圆中,能够互相重合的弧叫做等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
前提
续表
知2-讲
感悟新知
特别提醒
1. 弦与直径的关系:直径是圆中最长的弦,但弦不一定是直径.
2. 弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦和弧都有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条.
感悟新知
知2-练
下列语句中:①直径是弦;②弦是直径;③半径相等
的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有 ____________.
①③⑤
例 3
知2-练
感悟新知
3-1. 如图,在⊙ O 中,点A,O,D 在一条直线上, 点B,O,C 在一条直线上,那么图中有________条弦.
3
知识点
点和圆的位置关系
知3-讲
感悟新知
3
点和圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等级关系
点在圆外 点到圆心的距离大于半径
点在圆上 点到圆心的距离等于半径
点在圆内 点到圆心的距离小于半径
知3-讲
感悟新知
特别提醒
符号“ ”读作“等价于”,它表示符号“ ”左右两端互为因果关系.
感悟新知
知3-练
如图3-1-2,已知⊙ O 的半径r=5 cm,圆心O 到直线l 的距离d=OD=3 cm,在直线l 上有P,Q,R 三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的?
例 4
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
知3-练
感悟新知
解:如图3-1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP=5 cm=r. ∴点P 在⊙ O 上.
∵ QD=5 cm,∴ OQ= cm>5 cm,∴点Q 在⊙ O 外.
∵ RD=3 cm,∴ OR=3 cm<5 cm. ∴点R 在⊙ O 内.
知3-练
感悟新知
4-1. 在矩形ABCD 中,AB=8,AD=6,以顶点D 为圆心作半径为r 的圆,若要求另外三个顶点A,B,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是 ________.
6
1. 有下列说法:①同圆中,所有的半径都相等;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆. 其中正确的说法有( )
A. 1个 B. 2个
C. 3个 D. 4个
C
返回
D
返回
3. 如图,点A,D,G,M在半圆O上,四边形ABOC,四边形DEOF,四边形HMNO均为矩形,设BC=a,EF=b,NH=c,则下列选项正确的是( )
A. a>b>c
B. a=b=c
C. c>a>b
D. b>c>a
B
返回
4. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法中不正确的是( )
A. 当a<5时,点B在⊙A内
B. 当1<a<5时,点B在⊙A内
C. 当a<1时,点B在⊙A外
D. 当a>5时,点B在⊙A外
A
返回
5. [教材P66随堂练习T2]如图是某同学在体育课上投掷四次铅球的成绩示意图,该同学投掷铅球最好成绩的点为________. (填C,D,E,F中的一个字母)
F
返回
6. 在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以r=3为半径作圆,并判断A,B两点和⊙C的位置关系.
【解】如图.∵∠C=90°,AC=4,
AB=5,∴BC=3.
∵AC=4>r,∴点A在⊙C外.
∵BC=r,∴点B在⊙C上.
返回
7. 在平面直角坐标系中,已知⊙O的圆心与原点重合,半径为5,则下列各点中,不在圆上的点是( )
A. (4,3) B. (1,-4)
C. (-3,4) D. (-5,0)
B
课堂小结
圆
圆
弦、弧、等圆、等弧
两要素
位置
大小
圆心
半径
相关概念
点与圆的位置关系
点在圆上、圆内、圆外
谢谢观看!
