3.3 垂径定理 课件(共27张PPT)
文档属性
| 名称 | 3.3 垂径定理 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:17:10 | ||
图片预览








文档简介
(共27张PPT)
3.3 垂径定理
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
垂径定理
1. 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
特别提醒
1. “垂直于弦的直径”中的“直径”,其实质是:过圆心且垂直于弦的线段或直线.
2. “两条弧”是指弦所对的劣弧和优弧或两个半圆.
知1-讲
感悟新知
2. 示例:如图3-3-1,CD ⊥ AB 于点E,CD是⊙ O 的直径,那么可用几何语言表述为
表述为 CD是直径
CD⊥AB
︵
︵
︵
︵
感悟新知
知1-练
如图3-3-2,弦CD 垂直于⊙ O 的直径AB,垂足为点H,且CD=2,BD=,则AB 的长为( )
A. 2
B. 3
C. 4
D. 5
例 1
感悟新知
知1-练
解题秘方:构造垂径定理的基本图形解题. 把半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形里是解题的关键.
解:连接OD,如图3-3-2.
∵ CD ⊥ AB,CD=2,
∴ CH=DH=.
感悟新知
知1-练
在Rt △ BHD 中,由勾股定理,得BH=1.
设⊙O的半径为r,
在Rt △OHD 中,OH2+HD2=OD2,
即(r-1)2+()2=r2,
解得r=. ∴ AB=3.
利用勾股定理列方程
答案:B
感悟新知
知1-练
1-1. [中考·东营]“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺. 问:径几何?”转化为现在的数学语言表达就
是:如图,CD为⊙O的直径,弦AB⊥
CD,垂足为E,CE=1 寸,AB= 10 寸,
则直径CD的长度为 ______寸.
26
感悟新知
知1-练
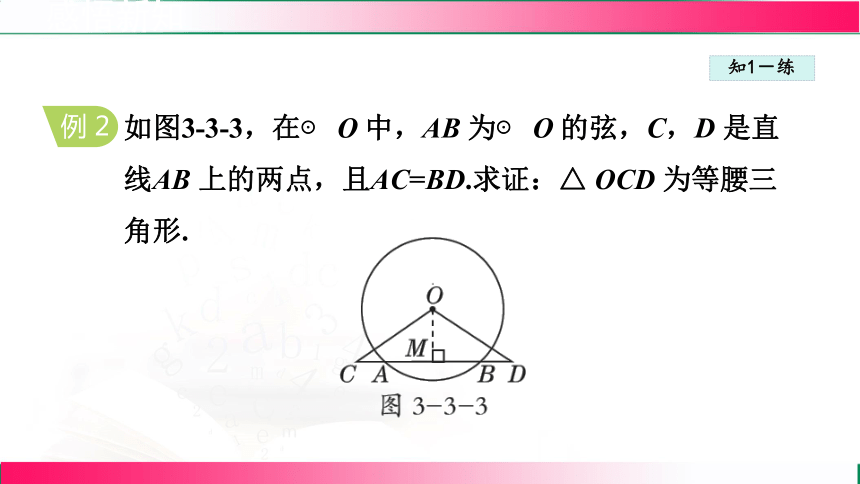
如图3-3-3,在⊙ O 中,AB 为⊙ O 的弦,C,D 是直
线AB 上的两点,且AC=BD.求证:△ OCD 为等腰三角形.
例 2
感悟新知
知1-练
证明:过点O 作OM ⊥ AB,垂足为M,如图3-3-3.
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,
∴ OC=OD.
∴△ OCD 为等腰三角形.
知识点
垂径定理的推论
知2-讲
感悟新知
2
1. 推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知2-讲
感悟新知
2. 示例 如图3-3-4,CD 是⊙ O 的直径,AB 是弦(非直径),AB 与CD 相交于点E,且AE=BE,那么CD 垂直于AB,并且AC = CB,AD = DB .可用几何语言表述为
CD是直径 CD⊥AB,
AE=BE AD = BD,
AB不是直径 AC = BC .
︵
︵
︵
︵
︵
︵
︵
︵
感悟新知
知2-练
如图3-3-5,AB,CD 是⊙ O 的弦,M,N 分别为
AB,CD 的中点,且∠ AMN = ∠ CNM. 求证:AB=CD.
例 3
解题秘方:紧扣弦的中点作符合垂径定理推论的基本图形,再结合全等三角形的判定和性质进行证明.
知2-练
感悟新知
证明:如图3-3-5,连接OM,ON,OA,OC.
∵ O 为圆心,且M,N 分别为AB,CD 的中点,
∴ AB=2AM,CD=2CN,OM ⊥ AB,ON ⊥ CD.
∴∠ OMA= ∠ ONC=90° .
∵∠ AMN= ∠ CNM,
∴∠ OMN= ∠ ONM.∴ OM=ON.
又∵ OA=OC,∴ Rt△OAM ≌ Rt△OCN(HL).
∴ AM=CN. ∴ AB=CD.
感悟新知
知2-练
3-1. 如图, ⊙ O 的弦AB=12,M 是AB 的中点, 且OM= 2, 则⊙ O 的半径等于________.
感悟新知
知2-练
4-1. [中考·广西] 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37 m,拱高约为7 m,则赵州桥主桥拱半径R约为( )
A. 20 m B. 28 m
C. 35 m D. 40 m
B
感悟新知
知2-练
如图3-3-7,一条公路的转弯处是一段圆弧(AB),点O 是这段弧所在圆的圆心,点C 是AB的中点,半径OC 与AB相交于点D,AB=120 m,CD=20 m,求这段弯路所在圆的半径.
例 5
解题秘方:紧扣垂径定理的推论,利用“平分弧,且经过圆心”推出“垂直平分弦”,结合勾股定理求出半径的长.
︵
︵
知2-练
感悟新知
解:连接OB,如图3-3-7.
∵点C 是AB的中点,
∴ OC⊥AB,AD=BD=AB=60 m.
设OB=OC=r m,
在Rt△OBD中,OB2=OD2+BD2,
∴ r2=(r-20)2+602,
∴ r=100,即这段弯路所在圆的半径为100 m.
︵
返回
1. [2024濮阳期末]如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.若AD=CD=4,OD=3,则BD的长为( )
A. 2 B. 3
C. 4 D. 1
A
返回
2. 下列命题正确的有( )
①平分弦所对的两条弧的直线必垂直于弦;②垂直于弦的直线平分弦;
③平分弦的直线必平分弦所对的两条弧;
④与直径不垂直的弦不能被该直径平分;
⑤平分弦的直径必平分弦所对的两条弧.
A. 1个 B. 2个 C. 3个 D. 4个
A
返回
D
返回
8
5. 如图①所示为丁字尺,它是一种作图工具,可以看作由两把互相垂直的直尺组成,并且CD部分平分AB部分. 现在将丁字尺放在一个圆形工件上(圆心为O),如图②所示,使得A,B,D分别落在⊙O
上,这样圆心O就会落在CD上,
已知AB=CD=8 cm,请求出该
圆形工件的半径.
返回
返回
C
课堂小结
垂径定理
平分弦
垂径定理
垂径定理的推论
平分弦所
对的弧
垂直于弦
谢谢观看!
3.3 垂径定理
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
垂径定理
1. 垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
特别提醒
1. “垂直于弦的直径”中的“直径”,其实质是:过圆心且垂直于弦的线段或直线.
2. “两条弧”是指弦所对的劣弧和优弧或两个半圆.
知1-讲
感悟新知
2. 示例:如图3-3-1,CD ⊥ AB 于点E,CD是⊙ O 的直径,那么可用几何语言表述为
表述为 CD是直径
CD⊥AB
︵
︵
︵
︵
感悟新知
知1-练
如图3-3-2,弦CD 垂直于⊙ O 的直径AB,垂足为点H,且CD=2,BD=,则AB 的长为( )
A. 2
B. 3
C. 4
D. 5
例 1
感悟新知
知1-练
解题秘方:构造垂径定理的基本图形解题. 把半径、圆心到弦的垂线段、弦的一半构建在一个直角三角形里是解题的关键.
解:连接OD,如图3-3-2.
∵ CD ⊥ AB,CD=2,
∴ CH=DH=.
感悟新知
知1-练
在Rt △ BHD 中,由勾股定理,得BH=1.
设⊙O的半径为r,
在Rt △OHD 中,OH2+HD2=OD2,
即(r-1)2+()2=r2,
解得r=. ∴ AB=3.
利用勾股定理列方程
答案:B
感悟新知
知1-练
1-1. [中考·东营]“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺. 问:径几何?”转化为现在的数学语言表达就
是:如图,CD为⊙O的直径,弦AB⊥
CD,垂足为E,CE=1 寸,AB= 10 寸,
则直径CD的长度为 ______寸.
26
感悟新知
知1-练
如图3-3-3,在⊙ O 中,AB 为⊙ O 的弦,C,D 是直
线AB 上的两点,且AC=BD.求证:△ OCD 为等腰三角形.
例 2
感悟新知
知1-练
证明:过点O 作OM ⊥ AB,垂足为M,如图3-3-3.
∵ OM ⊥ AB,∴ AM=BM.
∵ AC=BD,∴ CM=DM.
又∵ OM ⊥ CD,
∴ OC=OD.
∴△ OCD 为等腰三角形.
知识点
垂径定理的推论
知2-讲
感悟新知
2
1. 推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知2-讲
感悟新知
2. 示例 如图3-3-4,CD 是⊙ O 的直径,AB 是弦(非直径),AB 与CD 相交于点E,且AE=BE,那么CD 垂直于AB,并且AC = CB,AD = DB .可用几何语言表述为
CD是直径 CD⊥AB,
AE=BE AD = BD,
AB不是直径 AC = BC .
︵
︵
︵
︵
︵
︵
︵
︵
感悟新知
知2-练
如图3-3-5,AB,CD 是⊙ O 的弦,M,N 分别为
AB,CD 的中点,且∠ AMN = ∠ CNM. 求证:AB=CD.
例 3
解题秘方:紧扣弦的中点作符合垂径定理推论的基本图形,再结合全等三角形的判定和性质进行证明.
知2-练
感悟新知
证明:如图3-3-5,连接OM,ON,OA,OC.
∵ O 为圆心,且M,N 分别为AB,CD 的中点,
∴ AB=2AM,CD=2CN,OM ⊥ AB,ON ⊥ CD.
∴∠ OMA= ∠ ONC=90° .
∵∠ AMN= ∠ CNM,
∴∠ OMN= ∠ ONM.∴ OM=ON.
又∵ OA=OC,∴ Rt△OAM ≌ Rt△OCN(HL).
∴ AM=CN. ∴ AB=CD.
感悟新知
知2-练
3-1. 如图, ⊙ O 的弦AB=12,M 是AB 的中点, 且OM= 2, 则⊙ O 的半径等于________.
感悟新知
知2-练
4-1. [中考·广西] 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37 m,拱高约为7 m,则赵州桥主桥拱半径R约为( )
A. 20 m B. 28 m
C. 35 m D. 40 m
B
感悟新知
知2-练
如图3-3-7,一条公路的转弯处是一段圆弧(AB),点O 是这段弧所在圆的圆心,点C 是AB的中点,半径OC 与AB相交于点D,AB=120 m,CD=20 m,求这段弯路所在圆的半径.
例 5
解题秘方:紧扣垂径定理的推论,利用“平分弧,且经过圆心”推出“垂直平分弦”,结合勾股定理求出半径的长.
︵
︵
知2-练
感悟新知
解:连接OB,如图3-3-7.
∵点C 是AB的中点,
∴ OC⊥AB,AD=BD=AB=60 m.
设OB=OC=r m,
在Rt△OBD中,OB2=OD2+BD2,
∴ r2=(r-20)2+602,
∴ r=100,即这段弯路所在圆的半径为100 m.
︵
返回
1. [2024濮阳期末]如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.若AD=CD=4,OD=3,则BD的长为( )
A. 2 B. 3
C. 4 D. 1
A
返回
2. 下列命题正确的有( )
①平分弦所对的两条弧的直线必垂直于弦;②垂直于弦的直线平分弦;
③平分弦的直线必平分弦所对的两条弧;
④与直径不垂直的弦不能被该直径平分;
⑤平分弦的直径必平分弦所对的两条弧.
A. 1个 B. 2个 C. 3个 D. 4个
A
返回
D
返回
8
5. 如图①所示为丁字尺,它是一种作图工具,可以看作由两把互相垂直的直尺组成,并且CD部分平分AB部分. 现在将丁字尺放在一个圆形工件上(圆心为O),如图②所示,使得A,B,D分别落在⊙O
上,这样圆心O就会落在CD上,
已知AB=CD=8 cm,请求出该
圆形工件的半径.
返回
返回
C
课堂小结
垂径定理
平分弦
垂径定理
垂径定理的推论
平分弦所
对的弧
垂直于弦
谢谢观看!
