3.4 圆周角和圆心角的关系 课件(共31张PPT)
文档属性
| 名称 | 3.4 圆周角和圆心角的关系 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:33:06 | ||
图片预览











文档简介
(共31张PPT)
3.4 圆周角和圆心角的关系
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆周角
1. 圆周角的定义 顶点在圆上,两边分别与圆还有另一个交点,像这样的角,叫做圆周角.
特征 圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
知1-讲
感悟新知
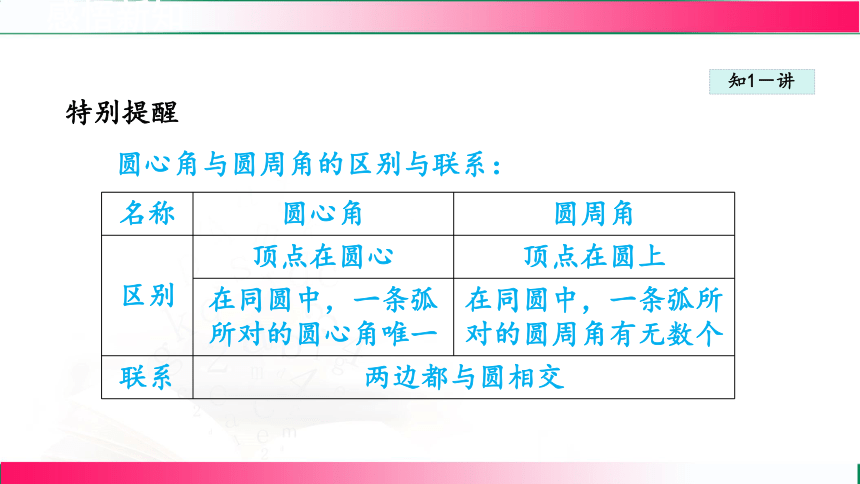
特别提醒
圆心角与圆周角的区别与联系:
名称 圆心角 圆周角
区别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交
知1-讲
感悟新知
2. 圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
如图3-4-1,∠ ACB=∠ AOB.
特别警示:定理中的圆周角与圆心
角是通过它们所对的同一条弧联系在一
起的,故不能把同一条弧这个前提省略.
感悟新知
知1-练
如图3-4-2,AB 是⊙ O 的直径, 弦BC=BD, 若
∠ BOD=50°,求∠ A 的度数.
例 1
解题秘方:连接OC,将求BC所对的圆周角的度数转化为求BC所对的圆心角的度数来解.
︵
︵
感悟新知
知1-练
解:连接OC,如图3-4-2.
∵ BC=BD,
∴∠ BOC= ∠ BOD=50°.
∴∠ A=∠BOC= ×50°=25°.
感悟新知
知1-练
1-1. [中考·河南]如图,点A,B,C在⊙O上,若∠ C=55°,则∠AOB的度数为( )
A. 95°
B. 100°
C. 105°
D. 110°
D
知识点
圆周角定理的推论
知2-讲
感悟新知
2
1. 推论1 同弧或等弧所对的圆周角相等.
特别提醒
“同弧或等弧”若改为“同弦或等弦”,结论就不成立了.因为一条弦(非直径)所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
知2-讲
感悟新知
2. 推论2 (1)直径所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
3. “五量关系”定理(拓展归纳)
在同圆或等圆中,如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
感悟新知
知2-练
[中考·兰州]如图3-4-3,△ABC内接于⊙O,CD是⊙O 的直径,∠ACD=40°,则∠B=( )
A. 70°
B. 60°
C. 50°
D. 40°
例 2
感悟新知
知2-练
2-1. [中考· 宜宾] 如图,已知点A,B,C在⊙O上,C为AB 的中点.若∠BAC=35°,则∠AOB 等于( )
A. 140°
B. 120°
C. 110°
D. 70°
︵
A
感悟新知
知2-练
如图3-4-4,AB 是⊙ O 的直径,BD 是⊙ O 的弦,延
长BD 到点C,使AC=AB. 求证:BD=CD.
解题秘方:紧扣“直径所对的圆周角是直角”,结合等腰三角形“三线合一”的性质求解.
例 3
知2-练
感悟新知
证明:如图3-4-4,连接AD.
∵ AB 是⊙ O 的直径,
∴∠ ADB=90°,即AD ⊥ BC.
又∵ AC=AB,∴ BD=CD.
感悟新知
知2-练
3-1. [中考· 珠海] 如图,AB是⊙O的直径,∠BAC=50°,则∠D=( )
A. 20°
B. 40°
C. 50°
D. 80°
B
感悟新知
知2-练
如图3-4-5,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且DE = BE,试判断△ABC的形状,并说明理由.
例 4
解题秘方:紧扣“等弧所对的圆周角相等”进行判断.
︵
︵
知2-练
感悟新知
解:△ABC为等腰三角形. 理由如下:
如图3-4-5,连接AE.
∵DE = BE ,∴∠CAE= ∠BAE.
∵ AB为半圆O的直径,
∴∠AEB= ∠AEC=90° .
又∵ AE=AE,∴△ABE ≌△ACE(ASA). ∴ AB=AC.
∴△ABC为等腰三角形.
︵
︵
知识点
圆内接四边形
知3-讲
感悟新知
3
1. 圆内接四边形
四边形ABCD 的四个顶点都在⊙ O 上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
特别解读
每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知3-讲
感悟新知
2. 圆周角定理的推论3
圆内接四边形的对角互补.
感悟新知
知3-练
[ 中考·常德]如图3-4-6,四边形ABCD 为⊙ O 的内接四边形,已知∠ BOD=100°,则∠ BCD 的度数为( )
A. 50°
B. 80°
C. 100°
D. 130°
例 5
返回
1. 如图,四边形ABCD的顶点A,B,C在圆上,且边CD与该圆交于点E,AC,BE交于点F.下列角中,弧AE所对的圆周角是( )
A. ∠ADE
B. ∠AFE
C. ∠ABE
D. ∠ABC
C
返回
2. 如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A的度数为( )
A. 22°
B. 68°
C. 44°
D. 58°
C
返回
D
返回
4. [2024宿迁一模]如图,在⊙O中,∠AOB=100°,点C在劣弧AB上. 若∠ABC=18°,则∠BAC的度数为( )
A. 32°
B. 33°
C. 34°
D. 35°
A
5. 如图,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需要在圆形边缘上安装________台这样的监视器.
3
返回
【点拨】监视器的监控角度是65°,即圆周角∠A=65°,根据圆周角的度数等于它所对弧上的圆心角度数的一半,可知对应的圆心角的度数为130°,因为360÷130=2……100,所以要监控整个展厅,最少需要在圆形边缘上安装3台这样的监视器.
6. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
返回
(2)若OC=3,OA=5,求AB的长.
课堂小结
圆周角和圆心角的关系
圆周角
直径所对的圆周角
圆内接四边形性质
定义
定理
谢谢观看!
3.4 圆周角和圆心角的关系
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、弦、弧(优弧、劣弧、半圆)等,并通过图形让学生直观理解。
垂径定理
探究活动:将一个圆形纸片沿着任意一条直径对折,观察折痕两侧的部分能否完全重合。引导学生发现圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
进一步探究:在圆上任意画一条弦 AB,作直径 CD 垂直于 AB,垂足为 E。测量 AE、BE、弧 AC、弧 BC、弧 AD、弧 BD 的长度,你能发现什么规律?
猜想结论:垂径定理 —— 垂直于弦的直径平分弦,并且平分弦所对的两条弧。
证明定理:引导学生结合图形,利用等腰三角形三线合一的性质进行证明。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
圆心角、弧、弦之间的关系定理
展示圆心角的定义:顶点在圆心的角叫做圆心角。
探究活动:在同圆或等圆中,分别画出相等的圆心角∠AOB 和∠COD,观察它们所对的弧 AB 与弧 CD、弦 AB 与弦 CD 之间的关系。
猜想结论:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
证明定理:通过旋转、叠合等方法进行证明。
推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等。
圆周角定理及其推论
展示圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角。
探究活动:在圆中画出一个圆周角∠ACB 和它所对的弧 AB,再画出圆心角∠AOB,测量∠ACB 和∠AOB 的度数,你能发现它们之间的关系吗?改变圆周角的位置,重复上述操作,你有什么发现?
猜想结论:圆周角定理 —— 一条弧所对的圆周角等于它所对的圆心角的一半。
证明定理:分三种情况进行证明(圆心在圆周角的一边上、圆心在圆周角的内部、圆心在圆周角的外部)。
推论:同弧或等弧所对的圆周角相等;半圆(或直径)所对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆周角
1. 圆周角的定义 顶点在圆上,两边分别与圆还有另一个交点,像这样的角,叫做圆周角.
特征 圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
知1-讲
感悟新知
特别提醒
圆心角与圆周角的区别与联系:
名称 圆心角 圆周角
区别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交
知1-讲
感悟新知
2. 圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
如图3-4-1,∠ ACB=∠ AOB.
特别警示:定理中的圆周角与圆心
角是通过它们所对的同一条弧联系在一
起的,故不能把同一条弧这个前提省略.
感悟新知
知1-练
如图3-4-2,AB 是⊙ O 的直径, 弦BC=BD, 若
∠ BOD=50°,求∠ A 的度数.
例 1
解题秘方:连接OC,将求BC所对的圆周角的度数转化为求BC所对的圆心角的度数来解.
︵
︵
感悟新知
知1-练
解:连接OC,如图3-4-2.
∵ BC=BD,
∴∠ BOC= ∠ BOD=50°.
∴∠ A=∠BOC= ×50°=25°.
感悟新知
知1-练
1-1. [中考·河南]如图,点A,B,C在⊙O上,若∠ C=55°,则∠AOB的度数为( )
A. 95°
B. 100°
C. 105°
D. 110°
D
知识点
圆周角定理的推论
知2-讲
感悟新知
2
1. 推论1 同弧或等弧所对的圆周角相等.
特别提醒
“同弧或等弧”若改为“同弦或等弦”,结论就不成立了.因为一条弦(非直径)所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
知2-讲
感悟新知
2. 推论2 (1)直径所对的圆周角是直角;
(2)90°的圆周角所对的弦是直径.
3. “五量关系”定理(拓展归纳)
在同圆或等圆中,如果两个圆心角、两条弧、两条弧所对的圆周角、两条弦、两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
感悟新知
知2-练
[中考·兰州]如图3-4-3,△ABC内接于⊙O,CD是⊙O 的直径,∠ACD=40°,则∠B=( )
A. 70°
B. 60°
C. 50°
D. 40°
例 2
感悟新知
知2-练
2-1. [中考· 宜宾] 如图,已知点A,B,C在⊙O上,C为AB 的中点.若∠BAC=35°,则∠AOB 等于( )
A. 140°
B. 120°
C. 110°
D. 70°
︵
A
感悟新知
知2-练
如图3-4-4,AB 是⊙ O 的直径,BD 是⊙ O 的弦,延
长BD 到点C,使AC=AB. 求证:BD=CD.
解题秘方:紧扣“直径所对的圆周角是直角”,结合等腰三角形“三线合一”的性质求解.
例 3
知2-练
感悟新知
证明:如图3-4-4,连接AD.
∵ AB 是⊙ O 的直径,
∴∠ ADB=90°,即AD ⊥ BC.
又∵ AC=AB,∴ BD=CD.
感悟新知
知2-练
3-1. [中考· 珠海] 如图,AB是⊙O的直径,∠BAC=50°,则∠D=( )
A. 20°
B. 40°
C. 50°
D. 80°
B
感悟新知
知2-练
如图3-4-5,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且DE = BE,试判断△ABC的形状,并说明理由.
例 4
解题秘方:紧扣“等弧所对的圆周角相等”进行判断.
︵
︵
知2-练
感悟新知
解:△ABC为等腰三角形. 理由如下:
如图3-4-5,连接AE.
∵DE = BE ,∴∠CAE= ∠BAE.
∵ AB为半圆O的直径,
∴∠AEB= ∠AEC=90° .
又∵ AE=AE,∴△ABE ≌△ACE(ASA). ∴ AB=AC.
∴△ABC为等腰三角形.
︵
︵
知识点
圆内接四边形
知3-讲
感悟新知
3
1. 圆内接四边形
四边形ABCD 的四个顶点都在⊙ O 上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
特别解读
每一个圆都有无数个内接四边形,但并不是所有的四边形都有外接圆,只有对角互补的四边形才有外接圆.
知3-讲
感悟新知
2. 圆周角定理的推论3
圆内接四边形的对角互补.
感悟新知
知3-练
[ 中考·常德]如图3-4-6,四边形ABCD 为⊙ O 的内接四边形,已知∠ BOD=100°,则∠ BCD 的度数为( )
A. 50°
B. 80°
C. 100°
D. 130°
例 5
返回
1. 如图,四边形ABCD的顶点A,B,C在圆上,且边CD与该圆交于点E,AC,BE交于点F.下列角中,弧AE所对的圆周角是( )
A. ∠ADE
B. ∠AFE
C. ∠ABE
D. ∠ABC
C
返回
2. 如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A的度数为( )
A. 22°
B. 68°
C. 44°
D. 58°
C
返回
D
返回
4. [2024宿迁一模]如图,在⊙O中,∠AOB=100°,点C在劣弧AB上. 若∠ABC=18°,则∠BAC的度数为( )
A. 32°
B. 33°
C. 34°
D. 35°
A
5. 如图,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需要在圆形边缘上安装________台这样的监视器.
3
返回
【点拨】监视器的监控角度是65°,即圆周角∠A=65°,根据圆周角的度数等于它所对弧上的圆心角度数的一半,可知对应的圆心角的度数为130°,因为360÷130=2……100,所以要监控整个展厅,最少需要在圆形边缘上安装3台这样的监视器.
6. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
返回
(2)若OC=3,OA=5,求AB的长.
课堂小结
圆周角和圆心角的关系
圆周角
直径所对的圆周角
圆内接四边形性质
定义
定理
谢谢观看!
