3.8 圆内接正多边形 课件(共32张PPT)
文档属性
| 名称 | 3.8 圆内接正多边形 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:20:23 | ||
图片预览











文档简介
(共32张PPT)
3.8 圆内接正多边形
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆内接正多边形
1. 正多边形 各边相等、各角也相等的多边形是正多边形.
2. 圆内接正多边形 顶点都在同一个圆上的正多边形叫做圆内接正多边形,这个圆叫做该正多边形的外接圆.
知1-讲
感悟新知
3. 正多边形的有关概念
(1)正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的边心距:正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
知1-讲
感悟新知
拓宽视野
1. 任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆.
2. 任意多边形(边数大于3)不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
感悟新知
知1-练
如图3-8-1,三角形AOB 是正三角形,以点O 为圆心,OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
例 1
解题秘方:紧扣同圆中弧、圆心角的关系证明.
感悟新知
知1-练
证明:∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,
∴ ∠ FOA= ∠ OAB=60 °,∠ COB= ∠ OBA=60°.
∴ ∠AOB= ∠BOC= ∠COD= ∠DOE= ∠EOF=∠FOA=60°.
∴AB = BC = CD = DE = EF = FA .
∴六边形ABCDEF 为圆内接正六边形.
︵
︵
︵
︵
︵
︵
知识点
正多边形的有关计算
知2-讲
感悟新知
2
特别提醒
常见的正多边形的边长与半径的关系:
1.正六边形的边长等于其外接圆半径;
2.正三角形的边长等于其外接圆半径的倍;
3.正方形的边长等于其外接圆半径的倍.
知2-讲
感悟新知
1. 正n边形的每个内角都等于.
2. 正n边形的每个中心角都等于 .
3. 正n边形的每个外角都等于 .
知2-讲
感悟新知
4. 设正n边形的半径为R,边长为a,边心距为r,则:
(1)半径、边长、边心距的关系为R2=r2+ ()2;
(2)周长l=na;
(3)面积S=ar·n= lr.
感悟新知
知2-练
已知正六边形ABCDEF 的半径为6,求这个正六边
形的边长a、周长l 和面积S.
例 2
解题秘方:巧用正六边形的边长、半径等之间的关系进行计算.
知2-练
感悟新知
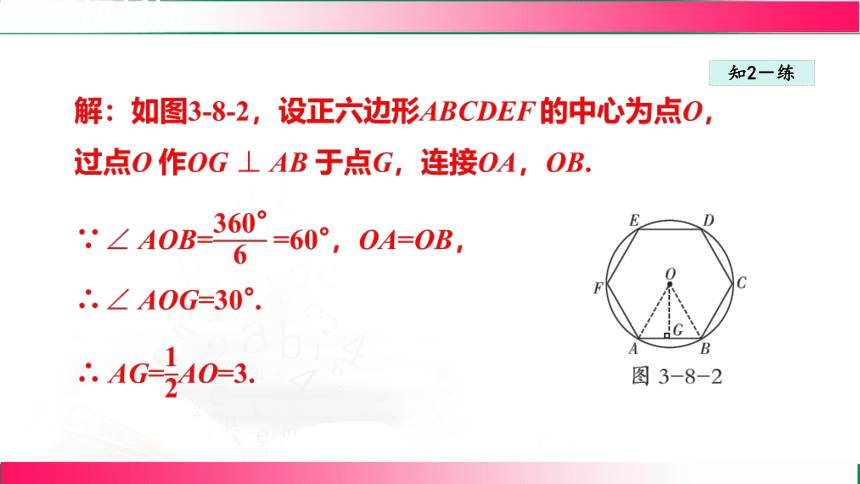
解:如图3-8-2,设正六边形ABCDEF 的中心为点O,
过点O 作OG ⊥ AB 于点G,连接OA,OB.
∵∠ AOB= =60°,OA=OB,
∴∠ AOG=30°.
∴ AG=AO=3.
知2-练
感悟新知
∴ a=AB=2AG=6.
∴ l=6a=6×6=36.
在Rt△AOG 中,OG= = =3,
∴ S=×AB×OG×6=×6×3×6=54 .
知2-练
感悟新知
2-1. [中考·成都] 如图,正六边形ABCDEF 内接于⊙ O,若⊙ O 的周长等于6π. 则正六边形的边长为( )
A.
B.
C. 3
D. 2
C
知识点
正多边形的画法
知3-讲
感悟新知
3
1. 正n 边形的画法:将圆n 等分,然后顺次连接各等分点,即得到所要作的正n 边形.
2. 对于一些特殊的正n 边形,如正方形、正六边形、正八边形,可以用圆规和直尺作图.
知3-讲
感悟新知
如图3-8-3 ①,在圆周上任定一点为圆心,以圆的半径为半径作弧,然后以弧与圆周的交点为圆心依次作弧,在圆周上得到6 个交点,依次连接,得到一个内接正六边形.
知3-讲
感悟新知
如图3-8-3 ②,在⊙O中用直尺和圆规作两条互相垂直的直径,就可把圆周四等分,从而作出正方形. 若再逐次平分各边所对的弧,就可以作边数逐次倍增的正多边形,如正八边形、正十六边形等.
知3-讲
感悟新知
特别提醒
1. 画圆内接正n边形,实质是找圆的n等分点.
2. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
感悟新知
知3-练
作一个正三角形,使其半径为0.9 cm .
例 3
解题秘方:用量角器画应先求出中心角,用尺规画则先考虑等分圆周.
知3-练
感悟新知
解:作法一 (1)作半径为0.9 cm 的⊙ O;
(2)用量角器画∠ AOB = ∠ BOC=120°,
其中A,B,C均为圆上的点;
(3)连接 AB,BC,CA,则
△ ABC 为所求作的正三角形,如图3-8-4
知3-练
感悟新知
作法二 (1)作半径为0.9 cm 的⊙ O;
(2)作⊙ O 的任一直径AB;
(3)以B 为圆心,以0.9 cm 为半径作弧,
交⊙ O 于D,E;
(4)连接AD,DE,EA,则△ ADE 为所
求作的正三角形,如图3-8-5.
返回
1. 下列说法正确的是( )
A. 正多边形既是轴对称图形又是中心对称图形
B. 正多边形的外接圆圆心是这个正多边形的中心
C. 正n边形的中心角与其每一个外角互补
D. 正五边形的边长等于其外接圆的半径
B
返回
C
3. [2024达州月考]如图,正方形ABCD是半径为r的⊙O的内接四边形,若r=6,则正方形ABCD的边心距为________.
返回
返回
4. [教材P98做一做]如图,已知⊙O,求作⊙O的内接正八边形. (不写作法,保留作图痕迹)
【解】如图所示.
返回
【答案】D
课堂小结
圆内接正多边形
正多边
形和圆
相关概念
中心
有关计算
画法
半径
中心角
边心距
谢谢观看!
3.8 圆内接正多边形
第三章 圆
北师大版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
展示生活中各种含有圆的图片,如车轮、摩天轮、圆形建筑等,引导学生观察并思考圆在生活中的广泛应用。
提问:“大家知道为什么车轮要做成圆形,而不是方形或其他形状呢?” 引发学生的好奇心和探究欲望,从而引出本节课的主题 —— 圆。
(二)讲授新课(30 分钟)
圆的定义及相关概念
动手操作:让学生用圆规在纸上画一个圆,引导学生观察画圆的过程,总结圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
介绍圆的其他相关概念,如直径、对的圆周角是直角,90° 的圆周角所对的弦是直径。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
知1-讲
感悟新知
1
圆内接正多边形
1. 正多边形 各边相等、各角也相等的多边形是正多边形.
2. 圆内接正多边形 顶点都在同一个圆上的正多边形叫做圆内接正多边形,这个圆叫做该正多边形的外接圆.
知1-讲
感悟新知
3. 正多边形的有关概念
(1)正多边形的中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的边心距:正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
知1-讲
感悟新知
拓宽视野
1. 任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆.
2. 任意多边形(边数大于3)不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
感悟新知
知1-练
如图3-8-1,三角形AOB 是正三角形,以点O 为圆心,OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
例 1
解题秘方:紧扣同圆中弧、圆心角的关系证明.
感悟新知
知1-练
证明:∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB,
∴ ∠ FOA= ∠ OAB=60 °,∠ COB= ∠ OBA=60°.
∴ ∠AOB= ∠BOC= ∠COD= ∠DOE= ∠EOF=∠FOA=60°.
∴AB = BC = CD = DE = EF = FA .
∴六边形ABCDEF 为圆内接正六边形.
︵
︵
︵
︵
︵
︵
知识点
正多边形的有关计算
知2-讲
感悟新知
2
特别提醒
常见的正多边形的边长与半径的关系:
1.正六边形的边长等于其外接圆半径;
2.正三角形的边长等于其外接圆半径的倍;
3.正方形的边长等于其外接圆半径的倍.
知2-讲
感悟新知
1. 正n边形的每个内角都等于.
2. 正n边形的每个中心角都等于 .
3. 正n边形的每个外角都等于 .
知2-讲
感悟新知
4. 设正n边形的半径为R,边长为a,边心距为r,则:
(1)半径、边长、边心距的关系为R2=r2+ ()2;
(2)周长l=na;
(3)面积S=ar·n= lr.
感悟新知
知2-练
已知正六边形ABCDEF 的半径为6,求这个正六边
形的边长a、周长l 和面积S.
例 2
解题秘方:巧用正六边形的边长、半径等之间的关系进行计算.
知2-练
感悟新知
解:如图3-8-2,设正六边形ABCDEF 的中心为点O,
过点O 作OG ⊥ AB 于点G,连接OA,OB.
∵∠ AOB= =60°,OA=OB,
∴∠ AOG=30°.
∴ AG=AO=3.
知2-练
感悟新知
∴ a=AB=2AG=6.
∴ l=6a=6×6=36.
在Rt△AOG 中,OG= = =3,
∴ S=×AB×OG×6=×6×3×6=54 .
知2-练
感悟新知
2-1. [中考·成都] 如图,正六边形ABCDEF 内接于⊙ O,若⊙ O 的周长等于6π. 则正六边形的边长为( )
A.
B.
C. 3
D. 2
C
知识点
正多边形的画法
知3-讲
感悟新知
3
1. 正n 边形的画法:将圆n 等分,然后顺次连接各等分点,即得到所要作的正n 边形.
2. 对于一些特殊的正n 边形,如正方形、正六边形、正八边形,可以用圆规和直尺作图.
知3-讲
感悟新知
如图3-8-3 ①,在圆周上任定一点为圆心,以圆的半径为半径作弧,然后以弧与圆周的交点为圆心依次作弧,在圆周上得到6 个交点,依次连接,得到一个内接正六边形.
知3-讲
感悟新知
如图3-8-3 ②,在⊙O中用直尺和圆规作两条互相垂直的直径,就可把圆周四等分,从而作出正方形. 若再逐次平分各边所对的弧,就可以作边数逐次倍增的正多边形,如正八边形、正十六边形等.
知3-讲
感悟新知
特别提醒
1. 画圆内接正n边形,实质是找圆的n等分点.
2. 尺规作图是一种比较准确的等分圆的方法,但只限于作一些特殊的正多边形.
感悟新知
知3-练
作一个正三角形,使其半径为0.9 cm .
例 3
解题秘方:用量角器画应先求出中心角,用尺规画则先考虑等分圆周.
知3-练
感悟新知
解:作法一 (1)作半径为0.9 cm 的⊙ O;
(2)用量角器画∠ AOB = ∠ BOC=120°,
其中A,B,C均为圆上的点;
(3)连接 AB,BC,CA,则
△ ABC 为所求作的正三角形,如图3-8-4
知3-练
感悟新知
作法二 (1)作半径为0.9 cm 的⊙ O;
(2)作⊙ O 的任一直径AB;
(3)以B 为圆心,以0.9 cm 为半径作弧,
交⊙ O 于D,E;
(4)连接AD,DE,EA,则△ ADE 为所
求作的正三角形,如图3-8-5.
返回
1. 下列说法正确的是( )
A. 正多边形既是轴对称图形又是中心对称图形
B. 正多边形的外接圆圆心是这个正多边形的中心
C. 正n边形的中心角与其每一个外角互补
D. 正五边形的边长等于其外接圆的半径
B
返回
C
3. [2024达州月考]如图,正方形ABCD是半径为r的⊙O的内接四边形,若r=6,则正方形ABCD的边心距为________.
返回
返回
4. [教材P98做一做]如图,已知⊙O,求作⊙O的内接正八边形. (不写作法,保留作图痕迹)
【解】如图所示.
返回
【答案】D
课堂小结
圆内接正多边形
正多边
形和圆
相关概念
中心
有关计算
画法
半径
中心角
边心距
谢谢观看!
