24.1.2中心对称和中心对称图形 课件(共31张PPT)
文档属性
| 名称 | 24.1.2中心对称和中心对称图形 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
24.1.2中心对称和中心对称图形
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解中心对称、中心对称图形的概念并能够区分它们的不同;
2.理解成中心对称图形的性质,并能作出一个图形关于某点成中心对称的对称图形;
3.经历中心对称的探索过程,通过观察、操作、发现,探究中心对称的有关概念和基本性质,培养学生的观察能力和动手操作能力;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
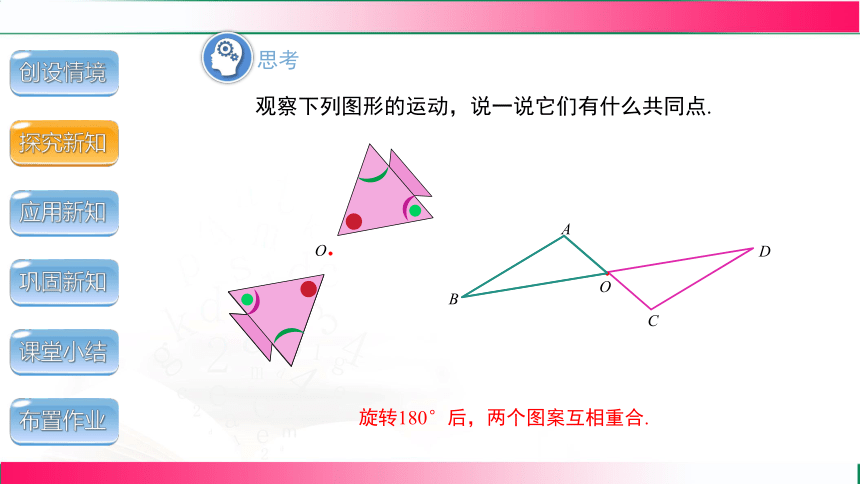
观察下列图形的运动,说一说它们有什么共同点.
O
O
A
B
D
C
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
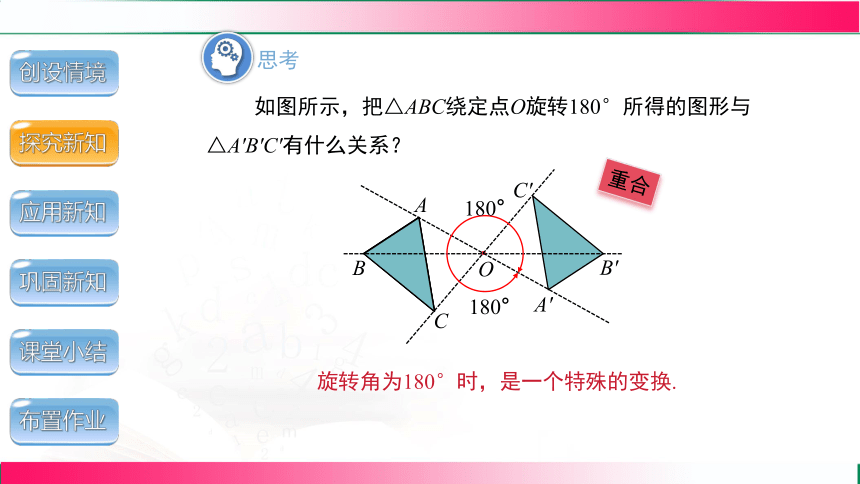
如图所示,把△ABC绕定点O旋转180°所得的图形与△A'B'C'有什么关系?
A
B
C
O
C'
B'
A'
180°
180°
旋转角为180°时,是一个特殊的变换.
重合
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
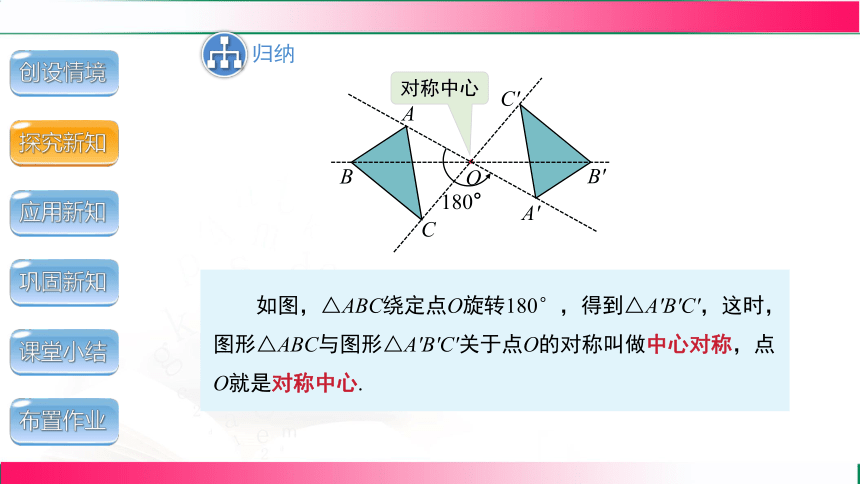
如图,△ABC绕定点O旋转180°,得到△A'B'C',这时,图形△ABC与图形△A'B'C'关于点O的对称叫做中心对称,点O就是对称中心.
A
B
C
O
C'
B'
A'
180°
对称中心
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
O
C'
B'
A'
180°
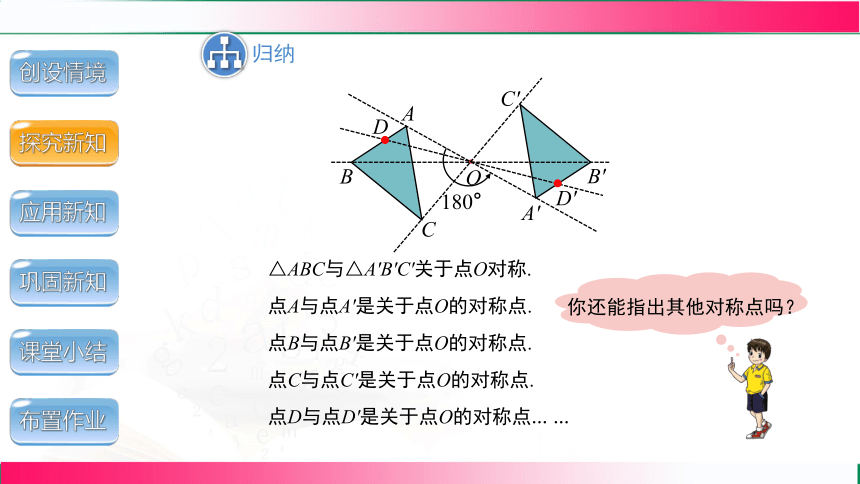
△ABC与△A'B'C'关于点O对称.
点A与点A'是关于点O的对称点.
点B与点B'是关于点O的对称点.
D
你还能指出其他对称点吗?
点D与点D'是关于点O的对称点… …
D'
点C与点C'是关于点O的对称点.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
O
C'
B'
A'
180°
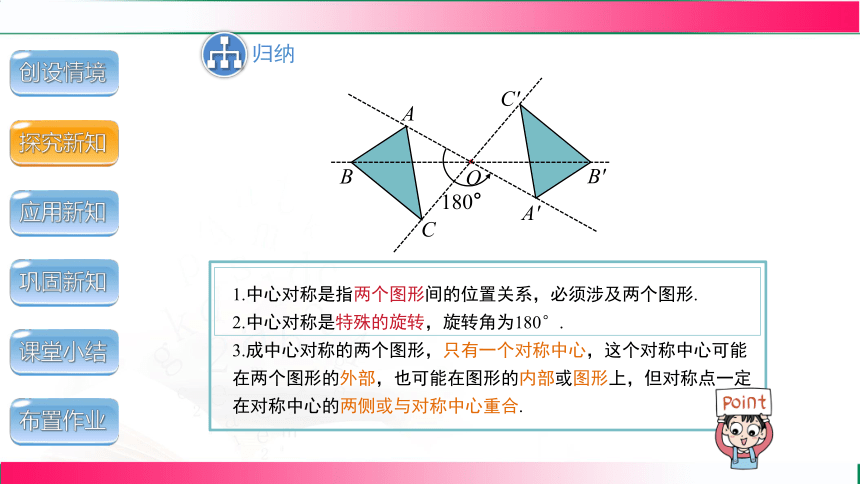
1.中心对称是指两个图形间的位置关系,必须涉及两个图形.
2.中心对称是特殊的旋转,旋转角为180°.
3.成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
两个图形成中心对称,除具有一般旋转的性质外,还有什么特性呢?
探究
A
B
C
A′
B′
C′
O
如图,△ABC与△A′B′C′关于点O对称.
分别连接AA′,BB′,CC′.
(1)点O在线段AA′上吗?如果在,在什么位置?
可知点A′是点A绕点O旋转_____得到的,即线段OA绕点O旋转180°得到线段______,则点____在线段AA′上,且OA=______,即点O是线段AA′的_______.
180°
OA′
O
OA′
中点
同样,点O也是线段BB′和CC′的_____.
中点
成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
两个图形成中心对称,除具有一般旋转的性质外,还有什么特性呢?
探究
A
B
C
A′
B′
C′
O
如图,△ABC与△A′B′C′关于点O对称.
分别连接AA′,BB′,CC′.
(2)△ABC与△A′B′C′有什么关系?
△ABC≌△A′B′C′.
中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称的性质:
1.成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
2. 中心对称的两个图形是全等的.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
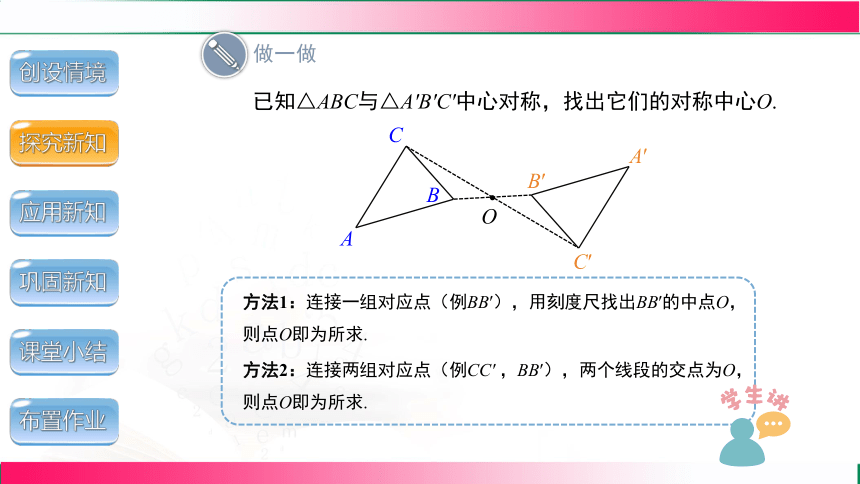
已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
O
方法1:连接一组对应点(例BB′),用刻度尺找出BB′的中点O,则点O即为所求.
方法2:连接两组对应点(例CC′ ,BB′),两个线段的交点为O,则点O即为所求.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
将下面的图形绕O点旋转180°,有什么共同点?
A
B
O
A
B
C
D
O
与原图形重合
把一个图形绕某一个定点旋转180°,如果旋转后的图形能够和原来图形重合,那么这个图形叫做中心对称图形,这个定点就是它的对称中心.互相重合的点叫做对称点.
注意:中心对称图形是指一个图形.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
O
A
B
C
D
O
线段AB是中心对称图形.
对称中心:线段AB的中点O.
A、B为对称点.
ABCD是中心对称图形.
对称中心:对角线的交点O.
A、C为对称点;B、D为对称点.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列图形是中心对称图形吗,如果是,指出对称中心?
矩形
菱形
正方形
O
O
O
矩形、菱形、正方形都是中心对称图形,
同时,它们还是轴对称图形,
它们的对称轴的交点就是对称中心.
中心对称 中心对称图形
联 系
区 别
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称与中心对称图形的区别与联系?
____个图形之间的关系.
具有某种性质的___个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成________.
对称点分别在___个图形上.
对称点在______个图形上.
若把中心对称的两个图形看作一个整体,则成为______________.
对称中心在___个图形之间.
对称中心在图形___或其_____.
中心对称和中心对称图形都是绕着某一点进行________后_____.
旋转180°
重合
中心对称
中心对称图形
两
一
两
同一
两
上
内部
归纳
例1 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
A
B
C
D
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
O
作法:
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
A'
B'
C'
D'
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
画出一个图形关于某点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
返回
1.[2024·邯郸期末]如图,在正方形网格中,A,B,C,D,E,F,G,H,M,N是网格线交点,△ABC与△DEF关于某点成中心对称,则其对称中心是( )
A.点G
B.点H
C.点M
D.点N
C
返回
2.如图,△ABC与△A′B′C′关于点O成中心对称,则下列不成立的是( )
A.OC=OC′
B.∠ABC=∠A′B′C′
C.CC′=BB′
D.BC∥B′C′
C
返回
3.如图,△AB′C′是△ABC绕点A旋转180°后得到的,已知∠B=90°,AB=1,∠C=30°,则CC′的长为 ________.
4
4.如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3),B(4,2),C(3,4).
(1)将△ABC沿水平方向向左平移4个单位长度得到△A1B1C1,请画出△A1B1C1;
【解】如图,△A1B1C1即为所求;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,并直接写出B2,C2的坐标;
【解】如图,△A2B2C2即为所求.点B2的坐标为(-4,-2),点C2的坐标为(-3,-4).
返回
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是________________.
(-2,0)
返回
5. 2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
D
返回
6.如图,△ABC与△CDA关于点O成中心对称,过点O作任意直线EF,分别交AD,BC于点E,F,下面的结论:
①点E和点F,点B和点D分别关于点O成中心对称;
②直线BD必经过点O;
③四边形ABCD是中心对称图形;
④四边形DEOC与四边形BFOA的
面积必相等;⑤△AOE与△COF成中心对称.
其中正确的个数为( )
A.2 B.3 C.4 D.5
D
7.下列图案中是旋转对称图形,但不是中心对称图形的是( )
A
【点易错】注意中心对称图形是旋转对称图形的特例,当旋转对称图形绕某一个定点旋转180°后能与原图形重合时,该图形是中心对称图形.
返回
中心对称的性质
1.成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
2. 中心对称的两个图形是全等的.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称和中心对称图形
中心对称图形
把一个图形绕某一个定点旋转180°,如果旋转后的图形能够和原来图形重合,那么这个图形叫做中心对称图形.
中心对称
如图,△ABC绕定点O旋转180°得到△A'B'C' ,图形△ABC与图形△A'B'C'关于点O的对称叫做中心对称.
布置作业
教科书第6页
练习第1,2(4)题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
24.1.2中心对称和中心对称图形
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解中心对称、中心对称图形的概念并能够区分它们的不同;
2.理解成中心对称图形的性质,并能作出一个图形关于某点成中心对称的对称图形;
3.经历中心对称的探索过程,通过观察、操作、发现,探究中心对称的有关概念和基本性质,培养学生的观察能力和动手操作能力;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
观察下列图形的运动,说一说它们有什么共同点.
O
O
A
B
D
C
旋转180°后,两个图案互相重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图所示,把△ABC绕定点O旋转180°所得的图形与△A'B'C'有什么关系?
A
B
C
O
C'
B'
A'
180°
180°
旋转角为180°时,是一个特殊的变换.
重合
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
如图,△ABC绕定点O旋转180°,得到△A'B'C',这时,图形△ABC与图形△A'B'C'关于点O的对称叫做中心对称,点O就是对称中心.
A
B
C
O
C'
B'
A'
180°
对称中心
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
O
C'
B'
A'
180°
△ABC与△A'B'C'关于点O对称.
点A与点A'是关于点O的对称点.
点B与点B'是关于点O的对称点.
D
你还能指出其他对称点吗?
点D与点D'是关于点O的对称点… …
D'
点C与点C'是关于点O的对称点.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
C
O
C'
B'
A'
180°
1.中心对称是指两个图形间的位置关系,必须涉及两个图形.
2.中心对称是特殊的旋转,旋转角为180°.
3.成中心对称的两个图形,只有一个对称中心,这个对称中心可能在两个图形的外部,也可能在图形的内部或图形上,但对称点一定在对称中心的两侧或与对称中心重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
两个图形成中心对称,除具有一般旋转的性质外,还有什么特性呢?
探究
A
B
C
A′
B′
C′
O
如图,△ABC与△A′B′C′关于点O对称.
分别连接AA′,BB′,CC′.
(1)点O在线段AA′上吗?如果在,在什么位置?
可知点A′是点A绕点O旋转_____得到的,即线段OA绕点O旋转180°得到线段______,则点____在线段AA′上,且OA=______,即点O是线段AA′的_______.
180°
OA′
O
OA′
中点
同样,点O也是线段BB′和CC′的_____.
中点
成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
两个图形成中心对称,除具有一般旋转的性质外,还有什么特性呢?
探究
A
B
C
A′
B′
C′
O
如图,△ABC与△A′B′C′关于点O对称.
分别连接AA′,BB′,CC′.
(2)△ABC与△A′B′C′有什么关系?
△ABC≌△A′B′C′.
中心对称的两个图形是全等的.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称的性质:
1.成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
2. 中心对称的两个图形是全等的.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
已知△ABC与△A′B′C′中心对称,找出它们的对称中心O.
A
B
C
A′
B′
C′
O
方法1:连接一组对应点(例BB′),用刻度尺找出BB′的中点O,则点O即为所求.
方法2:连接两组对应点(例CC′ ,BB′),两个线段的交点为O,则点O即为所求.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
将下面的图形绕O点旋转180°,有什么共同点?
A
B
O
A
B
C
D
O
与原图形重合
把一个图形绕某一个定点旋转180°,如果旋转后的图形能够和原来图形重合,那么这个图形叫做中心对称图形,这个定点就是它的对称中心.互相重合的点叫做对称点.
注意:中心对称图形是指一个图形.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
O
A
B
C
D
O
线段AB是中心对称图形.
对称中心:线段AB的中点O.
A、B为对称点.
ABCD是中心对称图形.
对称中心:对角线的交点O.
A、C为对称点;B、D为对称点.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列图形是中心对称图形吗,如果是,指出对称中心?
矩形
菱形
正方形
O
O
O
矩形、菱形、正方形都是中心对称图形,
同时,它们还是轴对称图形,
它们的对称轴的交点就是对称中心.
中心对称 中心对称图形
联 系
区 别
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称与中心对称图形的区别与联系?
____个图形之间的关系.
具有某种性质的___个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成________.
对称点分别在___个图形上.
对称点在______个图形上.
若把中心对称的两个图形看作一个整体,则成为______________.
对称中心在___个图形之间.
对称中心在图形___或其_____.
中心对称和中心对称图形都是绕着某一点进行________后_____.
旋转180°
重合
中心对称
中心对称图形
两
一
两
同一
两
上
内部
归纳
例1 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
A
B
C
D
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
O
作法:
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
A'
B'
C'
D'
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
画出一个图形关于某点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点).
2. 做关键点关于旋转中心的对称点.
3. 顺次连接对应点,组成的图形为所求.
返回
1.[2024·邯郸期末]如图,在正方形网格中,A,B,C,D,E,F,G,H,M,N是网格线交点,△ABC与△DEF关于某点成中心对称,则其对称中心是( )
A.点G
B.点H
C.点M
D.点N
C
返回
2.如图,△ABC与△A′B′C′关于点O成中心对称,则下列不成立的是( )
A.OC=OC′
B.∠ABC=∠A′B′C′
C.CC′=BB′
D.BC∥B′C′
C
返回
3.如图,△AB′C′是△ABC绕点A旋转180°后得到的,已知∠B=90°,AB=1,∠C=30°,则CC′的长为 ________.
4
4.如图,在平面直角坐标系内,已知△ABC的三个顶点坐标分别为A(1,3),B(4,2),C(3,4).
(1)将△ABC沿水平方向向左平移4个单位长度得到△A1B1C1,请画出△A1B1C1;
【解】如图,△A1B1C1即为所求;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,并直接写出B2,C2的坐标;
【解】如图,△A2B2C2即为所求.点B2的坐标为(-4,-2),点C2的坐标为(-3,-4).
返回
(3)若△A1B1C1与△A2B2C2关于点P成中心对称,则点P的坐标是________________.
(-2,0)
返回
5. 2024年6月5日,是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动.下面四幅图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是( )
D
返回
6.如图,△ABC与△CDA关于点O成中心对称,过点O作任意直线EF,分别交AD,BC于点E,F,下面的结论:
①点E和点F,点B和点D分别关于点O成中心对称;
②直线BD必经过点O;
③四边形ABCD是中心对称图形;
④四边形DEOC与四边形BFOA的
面积必相等;⑤△AOE与△COF成中心对称.
其中正确的个数为( )
A.2 B.3 C.4 D.5
D
7.下列图案中是旋转对称图形,但不是中心对称图形的是( )
A
【点易错】注意中心对称图形是旋转对称图形的特例,当旋转对称图形绕某一个定点旋转180°后能与原图形重合时,该图形是中心对称图形.
返回
中心对称的性质
1.成中心对称的两个图形中,对应点的连线经过对称中心,而被对称中心平分.
2. 中心对称的两个图形是全等的.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称和中心对称图形
中心对称图形
把一个图形绕某一个定点旋转180°,如果旋转后的图形能够和原来图形重合,那么这个图形叫做中心对称图形.
中心对称
如图,△ABC绕定点O旋转180°得到△A'B'C' ,图形△ABC与图形△A'B'C'关于点O的对称叫做中心对称.
布置作业
教科书第6页
练习第1,2(4)题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
