24.1.3平面直角坐标系中的图形变换 课件(共36张PPT)
文档属性
| 名称 | 24.1.3平面直角坐标系中的图形变换 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览







文档简介
(共36张PPT)
24.1.3平面直角坐标系中
的图形变换
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题;
2.能够运用旋转、轴对称或平移进行简单的图案设计;
3.经历观察、操作、发现等过程,培养学生探究问题的能力,观察能力和动手操作能力;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
点P(x,y)关于x轴对称点P'(x, y),
点P(x,y)关于y轴对称点P''( x,y).
回顾
若A(3,2),你能直接说出点A分别关于x轴,y轴对称的点的坐标吗?
点A(3,2)关于x轴对称点A'(3, 2),
点A(3,2)关于y轴对称点A''( 3,2).
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
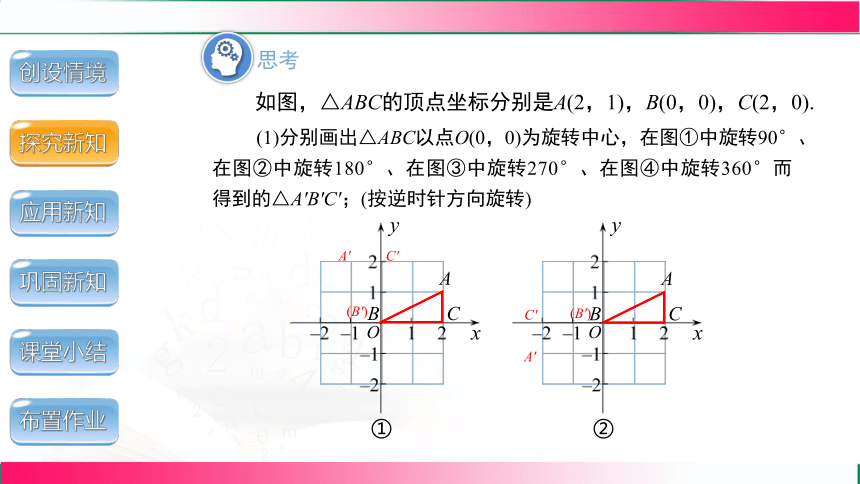
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图①中旋转90°、在图②中旋转180°、在图③中旋转270°、在图④中旋转360°而得到的△A′B′C′;(按逆时针方向旋转)
①
x
y
O
A
B
C
②
A'
(B')
C'
A'
(B')
C'
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
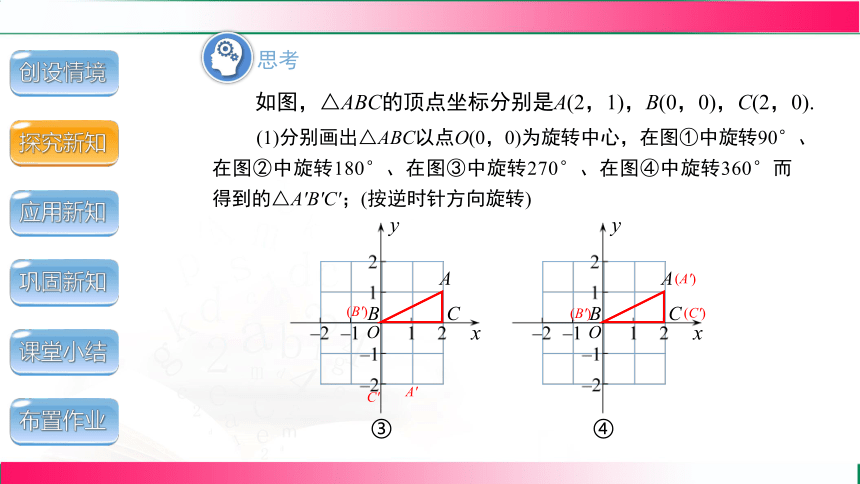
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图①中旋转90°、在图②中旋转180°、在图③中旋转270°、在图④中旋转360°而得到的△A′B′C′;(按逆时针方向旋转)
③
x
y
O
A
B
C
④
A'
(B')
C'
(A')
(B')
(C')
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
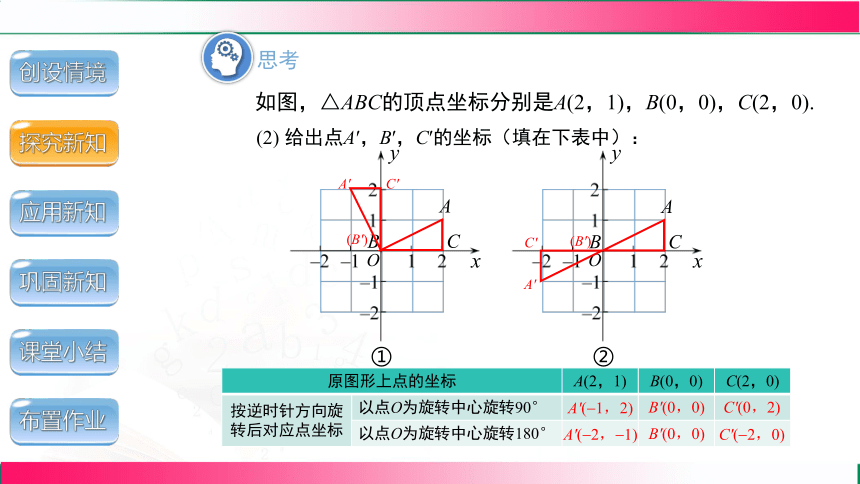
(2) 给出点A′,B′,C′的坐标(填在下表中):
①
x
y
O
A
B
C
②
A'
(B')
C'
A'
(B')
C'
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
A′( 1,2)
B′(0,0)
C′(0,2)
A′( 2, 1)
B′(0,0)
C′( 2,0)
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
(2) 给出点A′,B′,C′的坐标(填在下表中):
x
y
O
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′(1, 2)
B′(0,0)
C′(0, 2)
A′(2,1)
B′(0,0)
C′(2,0)
A
B
C
③
A
B
C
④
A'
(B')
C'
(A')
(B')
(C')
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
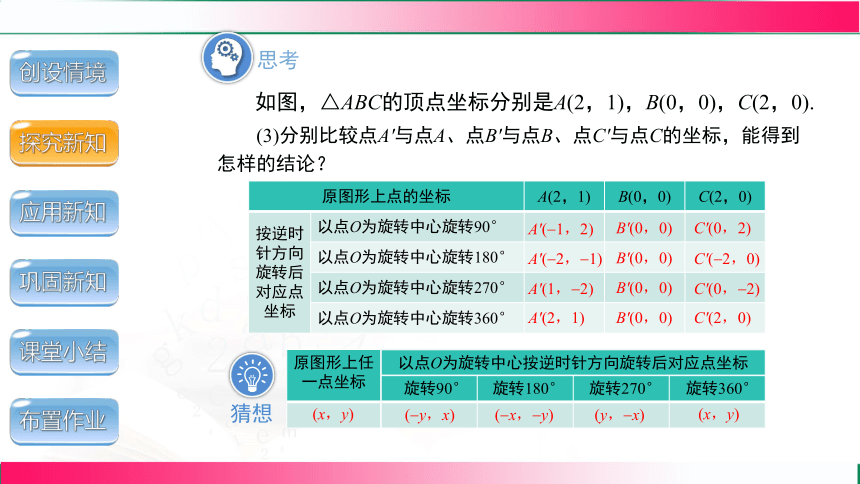
(3)分别比较点A′与点A、点B′与点B、点C′与点C的坐标,能得到怎样的结论?
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′( 1,2)
B′(0,0)
C′(0,2)
A′( 2, 1)
B′(0,0)
C′( 2,0)
A′(1, 2)
B′(0,0)
C′(0, 2)
A′(2,1)
B′(0,0)
C′(2,0)
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
猜想
证明猜想
x
y
O
P(x,y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
90°
B
A
证明:过点P,P1分别向x轴做垂线,垂足分别为A,B.
由题意知: POA P1OB 90°,
又∵ POA P 90°,
∴ P1OB P.
在Rt△POA和Rt△P1OB中
P1OB P, PAO P1BO 90°,PO P1O
∴△POA≌△P1OB.
∴P1B OA x,OB AP y.
结合图形,可得:P1( y,x).
x
y
P1( y,x)
P1
x
y
已知:如图,平面直角坐标系内任一点P(x,y),点P以点O为旋转中心按逆时针方向旋转90°后得到P1.
求证:P1( y,x)
180°
证明猜想
x
y
O
P(x,y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
P3(y, x)
270°
360°
(或P4)
C
A
证明:过点P,P2分别向x轴做垂线,垂足分别为A,C.
在Rt△POA和Rt△P2OC中
POA P2OC,
PAO P2CO 90°,
PO P2O,
∴△POA≌△P2OC.
∴OC OA x, P2C PA y.
结合图形,可得:P2( x, y).
x
y
P1( y,x)
x
y
P2( x, y)
P2
已知:如图,平面直角坐标系内任一点P(x,y),点P以点O为旋转中心按逆时针方向旋转180°后得到P2.
求证:P2( x, y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
x
y
O
P(x,y)
360°
(或P4)
x
y
O
A
B
C
(A')
(B')
(C')
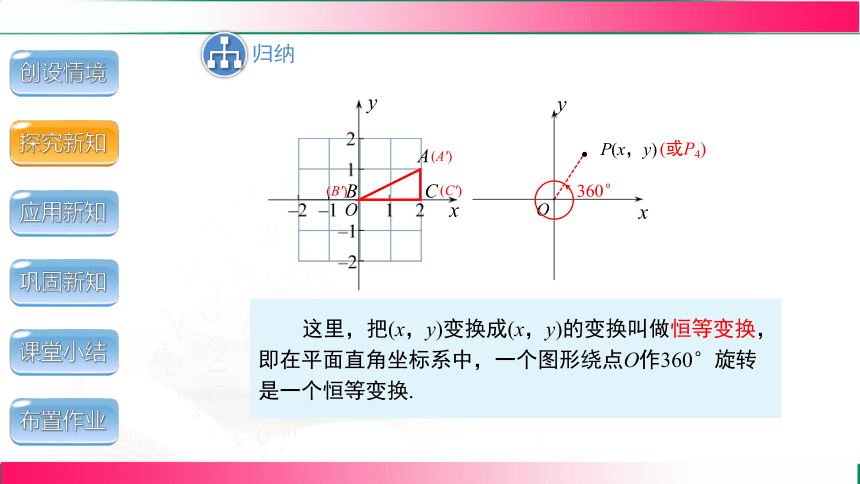
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,
即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
x
y
O
P(x,y)
180°
x
y
O
A
B
C
(B')
P(x,y)
A'
C'
P2( x, y)
P'( x, y)
关于原点O中心对称
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
已知点A的坐标为( 2,1),将点A绕着原点逆时针旋转,
直接写出下列情况下点A的对应点的坐标:
(1)绕着原点逆时针旋转90°,则点A的对应点A1的坐标是(_______);
(2)绕着原点逆时针旋转180°,则点A的对应点A2的坐标是(______);
(3)绕着原点逆时针旋转270°,则点A的对应点A3的坐标是(______);
(4)绕着原点逆时针旋转360°,则点A的对应点A4的坐标是(______).
1, 2
2, 1
1,2
2,1
抢答
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
图形变换的基本方式有哪些?
平移
轴对称
旋转
你能利用上述方式的一种或几种设计出美丽的图案吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
交流
(1)平移
(2)轴对称
(3)旋转180°
(4)轴对称并旋转180°
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
说出下列图案是由基本图形怎样变换得到的?
平移
平移
旋转
例1 如图,△ABC与△DEF关于原点O成中心对称,A( 1,2),C( 1,1),E(4, 3),请你直接写出点B、D、F的坐标.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
x
y
O
A
C
B
F
D
E
P(x,y)
P'( x, y)
关于原点O中心对称
解:由题意知:
B( 4,3),
D(1, 2),
F(1, 1).
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(1)作出关于AB所在直线的轴对称图形;
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
O
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(2)将你画出的部分连同原图形绕点O逆时针旋转90°;
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
O
利用平移、轴对称、旋转等变换设计图案,一般都是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
B
A
O
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
返回
A
2. 如图,点A的坐标是(-4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6)
B.(6,4)
C.(-6,-4)
D.(-4,-6)
返回
【答案】 B
返回
【答案】 D
4.[2024·德州德城区期末]如图,在正方形网格中,线段AB绕一点旋转一定的角度后与线段CD重合(C,D均为格点,点A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心的坐标为________.
(1,1)
返回
【点拨】如图,建立平面直角坐标系,连接AC,BD,作AC,BD的垂直平分线交于点E,点E即为旋转中心,E(1,1).
5.[2024·盐城一模]如图,在平面直角坐标系中,点A(3,0),点B(0,4),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,求线段OC的长度.
【解】如图,过点C作CD⊥x轴于点D,则∠ADC=
∠BOA=90°.
∵将线段AB绕点A顺时针
旋转90°得到线段AC,
∴∠BAC=90°,AC=AB.
∴∠BAO+∠CAD=90°.
返回
恒等变换
在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
旋转的应用
利用平移、轴对称、旋转设计图案
利用平移、轴对称、旋转等变换设计图案,一般是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
平面直角坐标系内图形的旋转变换
布置作业
教科书第11页
习题24.1第6,8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
24.1.3平面直角坐标系中
的图形变换
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题;
2.能够运用旋转、轴对称或平移进行简单的图案设计;
3.经历观察、操作、发现等过程,培养学生探究问题的能力,观察能力和动手操作能力;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
点P(x,y)关于x轴对称点P'(x, y),
点P(x,y)关于y轴对称点P''( x,y).
回顾
若A(3,2),你能直接说出点A分别关于x轴,y轴对称的点的坐标吗?
点A(3,2)关于x轴对称点A'(3, 2),
点A(3,2)关于y轴对称点A''( 3,2).
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图①中旋转90°、在图②中旋转180°、在图③中旋转270°、在图④中旋转360°而得到的△A′B′C′;(按逆时针方向旋转)
①
x
y
O
A
B
C
②
A'
(B')
C'
A'
(B')
C'
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图①中旋转90°、在图②中旋转180°、在图③中旋转270°、在图④中旋转360°而得到的△A′B′C′;(按逆时针方向旋转)
③
x
y
O
A
B
C
④
A'
(B')
C'
(A')
(B')
(C')
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
A
B
C
(2) 给出点A′,B′,C′的坐标(填在下表中):
①
x
y
O
A
B
C
②
A'
(B')
C'
A'
(B')
C'
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
A′( 1,2)
B′(0,0)
C′(0,2)
A′( 2, 1)
B′(0,0)
C′( 2,0)
x
y
O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
(2) 给出点A′,B′,C′的坐标(填在下表中):
x
y
O
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′(1, 2)
B′(0,0)
C′(0, 2)
A′(2,1)
B′(0,0)
C′(2,0)
A
B
C
③
A
B
C
④
A'
(B')
C'
(A')
(B')
(C')
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
(3)分别比较点A′与点A、点B′与点B、点C′与点C的坐标,能得到怎样的结论?
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′( 1,2)
B′(0,0)
C′(0,2)
A′( 2, 1)
B′(0,0)
C′( 2,0)
A′(1, 2)
B′(0,0)
C′(0, 2)
A′(2,1)
B′(0,0)
C′(2,0)
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
猜想
证明猜想
x
y
O
P(x,y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
90°
B
A
证明:过点P,P1分别向x轴做垂线,垂足分别为A,B.
由题意知: POA P1OB 90°,
又∵ POA P 90°,
∴ P1OB P.
在Rt△POA和Rt△P1OB中
P1OB P, PAO P1BO 90°,PO P1O
∴△POA≌△P1OB.
∴P1B OA x,OB AP y.
结合图形,可得:P1( y,x).
x
y
P1( y,x)
P1
x
y
已知:如图,平面直角坐标系内任一点P(x,y),点P以点O为旋转中心按逆时针方向旋转90°后得到P1.
求证:P1( y,x)
180°
证明猜想
x
y
O
P(x,y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
原图形上任一点坐标
(x,y)
以点O为旋转中心按逆时针方向旋转后对应点坐标
旋转90°
旋转180°
旋转270°
旋转360°
( y,x)
( x, y)
(y, x)
(x,y)
P3(y, x)
270°
360°
(或P4)
C
A
证明:过点P,P2分别向x轴做垂线,垂足分别为A,C.
在Rt△POA和Rt△P2OC中
POA P2OC,
PAO P2CO 90°,
PO P2O,
∴△POA≌△P2OC.
∴OC OA x, P2C PA y.
结合图形,可得:P2( x, y).
x
y
P1( y,x)
x
y
P2( x, y)
P2
已知:如图,平面直角坐标系内任一点P(x,y),点P以点O为旋转中心按逆时针方向旋转180°后得到P2.
求证:P2( x, y)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
x
y
O
P(x,y)
360°
(或P4)
x
y
O
A
B
C
(A')
(B')
(C')
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,
即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
x
y
O
P(x,y)
180°
x
y
O
A
B
C
(B')
P(x,y)
A'
C'
P2( x, y)
P'( x, y)
关于原点O中心对称
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
已知点A的坐标为( 2,1),将点A绕着原点逆时针旋转,
直接写出下列情况下点A的对应点的坐标:
(1)绕着原点逆时针旋转90°,则点A的对应点A1的坐标是(_______);
(2)绕着原点逆时针旋转180°,则点A的对应点A2的坐标是(______);
(3)绕着原点逆时针旋转270°,则点A的对应点A3的坐标是(______);
(4)绕着原点逆时针旋转360°,则点A的对应点A4的坐标是(______).
1, 2
2, 1
1,2
2,1
抢答
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
图形变换的基本方式有哪些?
平移
轴对称
旋转
你能利用上述方式的一种或几种设计出美丽的图案吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
交流
(1)平移
(2)轴对称
(3)旋转180°
(4)轴对称并旋转180°
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
说出下列图案是由基本图形怎样变换得到的?
平移
平移
旋转
例1 如图,△ABC与△DEF关于原点O成中心对称,A( 1,2),C( 1,1),E(4, 3),请你直接写出点B、D、F的坐标.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
x
y
O
A
C
B
F
D
E
P(x,y)
P'( x, y)
关于原点O中心对称
解:由题意知:
B( 4,3),
D(1, 2),
F(1, 1).
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(1)作出关于AB所在直线的轴对称图形;
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
O
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(2)将你画出的部分连同原图形绕点O逆时针旋转90°;
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
O
利用平移、轴对称、旋转等变换设计图案,一般都是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
B
A
O
例2 如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
返回
A
2. 如图,点A的坐标是(-4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6)
B.(6,4)
C.(-6,-4)
D.(-4,-6)
返回
【答案】 B
返回
【答案】 D
4.[2024·德州德城区期末]如图,在正方形网格中,线段AB绕一点旋转一定的角度后与线段CD重合(C,D均为格点,点A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心的坐标为________.
(1,1)
返回
【点拨】如图,建立平面直角坐标系,连接AC,BD,作AC,BD的垂直平分线交于点E,点E即为旋转中心,E(1,1).
5.[2024·盐城一模]如图,在平面直角坐标系中,点A(3,0),点B(0,4),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,求线段OC的长度.
【解】如图,过点C作CD⊥x轴于点D,则∠ADC=
∠BOA=90°.
∵将线段AB绕点A顺时针
旋转90°得到线段AC,
∴∠BAC=90°,AC=AB.
∴∠BAO+∠CAD=90°.
返回
恒等变换
在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
旋转的应用
利用平移、轴对称、旋转设计图案
利用平移、轴对称、旋转等变换设计图案,一般是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
平面直角坐标系内图形的旋转变换
布置作业
教科书第11页
习题24.1第6,8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
