24.2.1圆 课件(共32张PPT)
图片预览






文档简介
(共32张PPT)
24.2.1圆
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解圆、弧、弦等与圆有关的概念;并了解它们之间的区别与联系;
2.探索并掌握点和圆的位置关系,及这三种位置关系对应的圆的半径与点到圆心的距离之间的关系;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察
观察下列图形,都有哪些你熟悉的几何图形?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
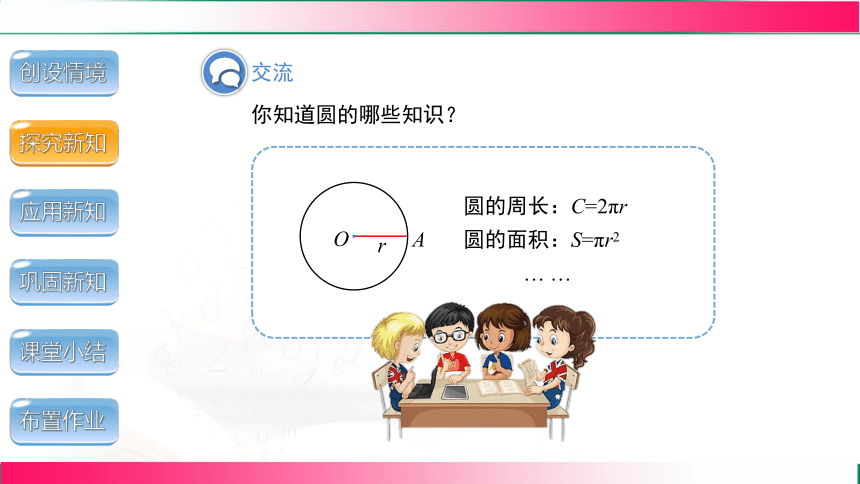
你知道圆的哪些知识?
交流
r
A
O
圆的周长:C=2πr
圆的面积:S=πr2
… …
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
你能试着总结出圆的概念吗?
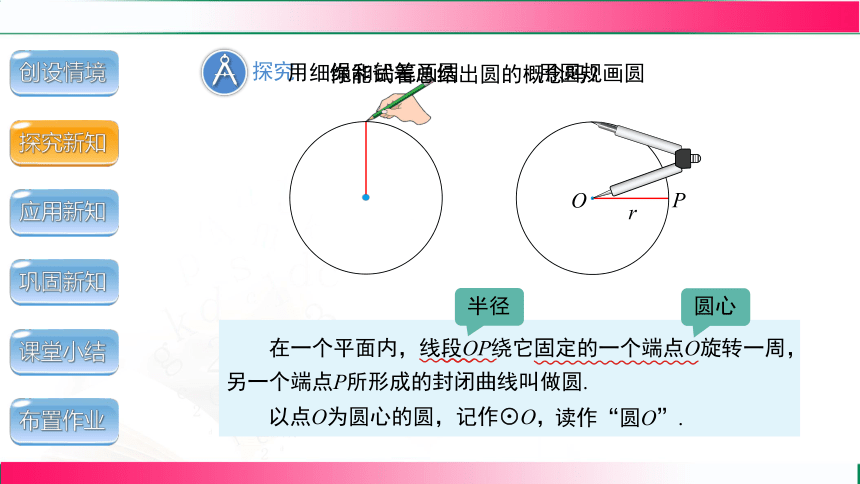
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的封闭曲线叫做圆.
P
O
圆心
半径
r
以点O为圆心的圆,记作⊙O,
读作“圆O”.
用细绳和铅笔画圆
用圆规画圆
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
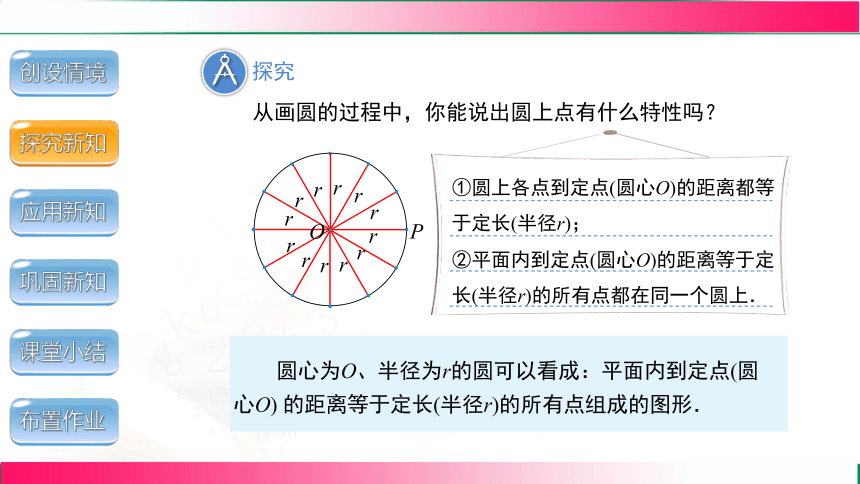
从画圆的过程中,你能说出圆上点有什么特性吗?
①圆上各点到定点(圆心O)的距离都等于定长(半径r);
P
r
②平面内到定点(圆心O)的距离等于定长(半径r)的所有点都在同一个圆上.
r
r
r
r
r
r
r
r
r
r
r
O
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的的图形叫做圆.
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
探究
你能回顾一下圆的两种定义吗?
动态定义
静态定义
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
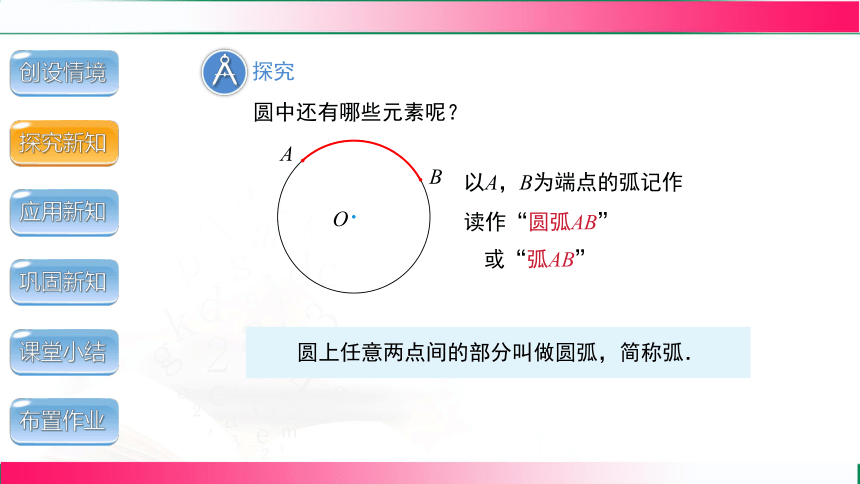
圆中还有哪些元素呢?
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A,B为端点的弧记作
读作“圆弧AB”
或“弧AB”
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
圆中还有哪些元素呢?
O
A
B
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
C
D
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
注意:直径是弦,但弦不一定是直径;
直径是最长的弦.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
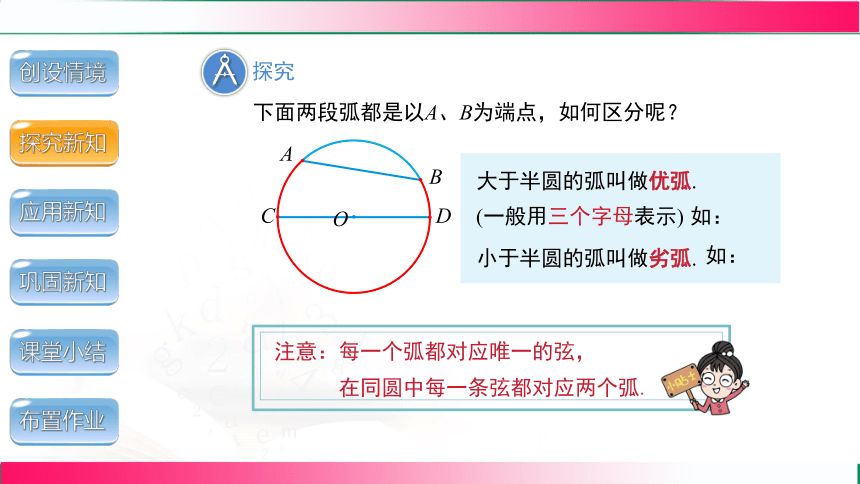
下面两段弧都是以A、B为端点,如何区分呢?
O
A
B
C
D
大于半圆的弧叫做优弧.
小于半圆的弧叫做劣弧.
(一般用三个字母表示)
如:
如:
注意:每一个弧都对应唯一的弦,
在同圆中每一条弦都对应两个弧.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
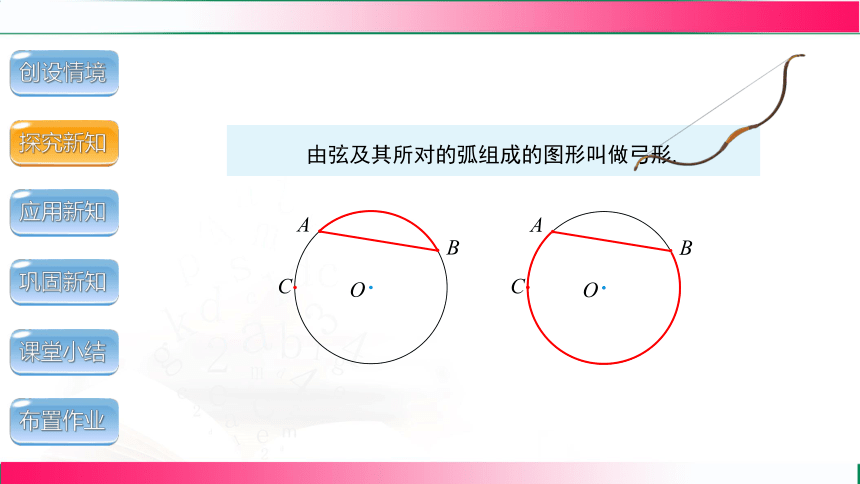
由弦及其所对的弧组成的图形叫做弓形.
O
A
B
C
O
A
B
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
下列每组中的两个圆能重合吗?
O1
O2
(1)
(2)
不重合
重合
能够重合的两个圆叫做等圆.
A
B
r
r
半径相等的两个圆是等圆.
反过来,同圆或等圆的半径相等.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
O
(1)
(2)
在同圆或等圆中,能够重合的弧叫做等弧.
O1
O2
B
A
D
C
平面上的圆把平面分成了哪几部分?
圆内
圆外
圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察点和圆的位置关系,能否对这六个点进行分类?
B
C
A
D
E
F
点C、F在圆外
点A、D在圆内
点B、E在圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
设⊙O的半径为r,OA,OB,OC与r有怎样的数量关系?
B
C
A
O
思考
OA<r
OB r
OC>r
r
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
点P在圆外
点P在圆内
点P在圆上
归纳
设⊙O的半径为r,点P到圆心的距离OP d
P
O
P
O
P
O
d<r
d r
d>r
位置关系
数量关系
点和圆的位置关系
符号“ ”读作“等价于”,它表示从符号左端可以推出右端,从右端也可以推出左端.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO .
5
圆外
圆内
≤5
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
例1 已知:如图,AB、CD为⊙O的直径,
求证:AD//CB.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
C
D
O
证明:连接AC,DB.
∵AB、CD为⊙O的直径,
∴OA OB,OC OD.
∴四边形ADBC为平行四边形.
∴AD//CB.
返回
1.下列条件中,能确定一个圆的是( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,10 cm长为半径
D.经过点A
C
2. 我国西汉中期的数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两钉子的内侧,转动
“矩”,则“矩”的顶点
C的运动路线将会是一个圆.
依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:_________________
_______________________________.
圆是平面内到定点的
距离等于定长的所有点组成的图形
返回
【点拨】连接AB,取AB的中点O,连接CO,则AO=BO=CO,即点A,B,C到点O的距离相等,所以“环矩以为圆”这种方法的道理是圆是平面内到定点的距离等于定长的所有点组成的图形.
返回
A
4.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( )
A.r>15 B.15C.15C
返回
5. 定义:点P,Q分别为两个图形G1,G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为图形G1和G2的“近距离”;如果线段PQ的长度存在最大值,就称该最大值为图形G1和G2的“远距离”.线段AB和⊙O是平面直角坐标系xOy中的两个图形,A(-3,4),B(-3,-4),⊙O的半径为1.
返回
下列关于线段AB与⊙O的说法中,正确的是( )
A.“近距离”是4
B.“近距离”是5
C.“远距离”是6
D.“远距离”是8
C
返回
6.如图,在⊙O中,______是直径,____________是弦,以E为端点的劣弧有______________________,以A为端点的优弧有__________________________.
AB
CD,EF,AB
与圆相关的概念
弧、弦、直径、半圆、优弧、劣弧、等圆、等弧、弓形
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
圆及其相关概念
圆的定义
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的的图形叫做圆.
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
点与圆的位置关系
点P在圆内
d<r
点P在圆上
d r
点P在圆外
d>r
布置作业
教科书第25页
习题24.2第1,2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
24.2.1圆
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解圆、弧、弦等与圆有关的概念;并了解它们之间的区别与联系;
2.探索并掌握点和圆的位置关系,及这三种位置关系对应的圆的半径与点到圆心的距离之间的关系;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察
观察下列图形,都有哪些你熟悉的几何图形?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
你知道圆的哪些知识?
交流
r
A
O
圆的周长:C=2πr
圆的面积:S=πr2
… …
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
你能试着总结出圆的概念吗?
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的封闭曲线叫做圆.
P
O
圆心
半径
r
以点O为圆心的圆,记作⊙O,
读作“圆O”.
用细绳和铅笔画圆
用圆规画圆
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
从画圆的过程中,你能说出圆上点有什么特性吗?
①圆上各点到定点(圆心O)的距离都等于定长(半径r);
P
r
②平面内到定点(圆心O)的距离等于定长(半径r)的所有点都在同一个圆上.
r
r
r
r
r
r
r
r
r
r
r
O
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的的图形叫做圆.
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
探究
你能回顾一下圆的两种定义吗?
动态定义
静态定义
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
圆中还有哪些元素呢?
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A,B为端点的弧记作
读作“圆弧AB”
或“弧AB”
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
圆中还有哪些元素呢?
O
A
B
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
C
D
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
注意:直径是弦,但弦不一定是直径;
直径是最长的弦.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
下面两段弧都是以A、B为端点,如何区分呢?
O
A
B
C
D
大于半圆的弧叫做优弧.
小于半圆的弧叫做劣弧.
(一般用三个字母表示)
如:
如:
注意:每一个弧都对应唯一的弦,
在同圆中每一条弦都对应两个弧.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
由弦及其所对的弧组成的图形叫做弓形.
O
A
B
C
O
A
B
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
下列每组中的两个圆能重合吗?
O1
O2
(1)
(2)
不重合
重合
能够重合的两个圆叫做等圆.
A
B
r
r
半径相等的两个圆是等圆.
反过来,同圆或等圆的半径相等.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
O
(1)
(2)
在同圆或等圆中,能够重合的弧叫做等弧.
O1
O2
B
A
D
C
平面上的圆把平面分成了哪几部分?
圆内
圆外
圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察点和圆的位置关系,能否对这六个点进行分类?
B
C
A
D
E
F
点C、F在圆外
点A、D在圆内
点B、E在圆上
思考
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
设⊙O的半径为r,OA,OB,OC与r有怎样的数量关系?
B
C
A
O
思考
OA<r
OB r
OC>r
r
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
点P在圆外
点P在圆内
点P在圆上
归纳
设⊙O的半径为r,点P到圆心的距离OP d
P
O
P
O
P
O
d<r
d r
d>r
位置关系
数量关系
点和圆的位置关系
符号“ ”读作“等价于”,它表示从符号左端可以推出右端,从右端也可以推出左端.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO .
5
圆外
圆内
≤5
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
例1 已知:如图,AB、CD为⊙O的直径,
求证:AD//CB.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
B
A
C
D
O
证明:连接AC,DB.
∵AB、CD为⊙O的直径,
∴OA OB,OC OD.
∴四边形ADBC为平行四边形.
∴AD//CB.
返回
1.下列条件中,能确定一个圆的是( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,10 cm长为半径
D.经过点A
C
2. 我国西汉中期的数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图①所示)的使用之道,其中就有“环矩以为圆”的方法.我国许多数学家对该方法作了如下更具体的描述:如图②所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两钉子的内侧,转动
“矩”,则“矩”的顶点
C的运动路线将会是一个圆.
依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:_________________
_______________________________.
圆是平面内到定点的
距离等于定长的所有点组成的图形
返回
【点拨】连接AB,取AB的中点O,连接CO,则AO=BO=CO,即点A,B,C到点O的距离相等,所以“环矩以为圆”这种方法的道理是圆是平面内到定点的距离等于定长的所有点组成的图形.
返回
A
4.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( )
A.r>15 B.15
返回
5. 定义:点P,Q分别为两个图形G1,G2上任一点,如果线段PQ的长度存在最小值,就称该最小值为图形G1和G2的“近距离”;如果线段PQ的长度存在最大值,就称该最大值为图形G1和G2的“远距离”.线段AB和⊙O是平面直角坐标系xOy中的两个图形,A(-3,4),B(-3,-4),⊙O的半径为1.
返回
下列关于线段AB与⊙O的说法中,正确的是( )
A.“近距离”是4
B.“近距离”是5
C.“远距离”是6
D.“远距离”是8
C
返回
6.如图,在⊙O中,______是直径,____________是弦,以E为端点的劣弧有______________________,以A为端点的优弧有__________________________.
AB
CD,EF,AB
与圆相关的概念
弧、弦、直径、半圆、优弧、劣弧、等圆、等弧、弓形
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
圆及其相关概念
圆的定义
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的的图形叫做圆.
圆心为O、半径为r的圆可以看成:平面内到定点(圆心O) 的距离等于定长(半径r)的所有点组成的图形.
点与圆的位置关系
点P在圆内
d<r
点P在圆上
d r
点P在圆外
d>r
布置作业
教科书第25页
习题24.2第1,2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
