24.2.2垂径分弦 课件(共24张PPT)
文档属性
| 名称 | 24.2.2垂径分弦 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
24.2.2垂径分弦
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.探索圆的对称性,进而得到垂径定理及其推论;
2.能利用垂径定理及其推论解决相关证明、计算及实际问题;
3.经历探索垂径定理及其推论的过程,发展推理能力,让学生领会数学的严谨性,培养学生实事求是的科学态度;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
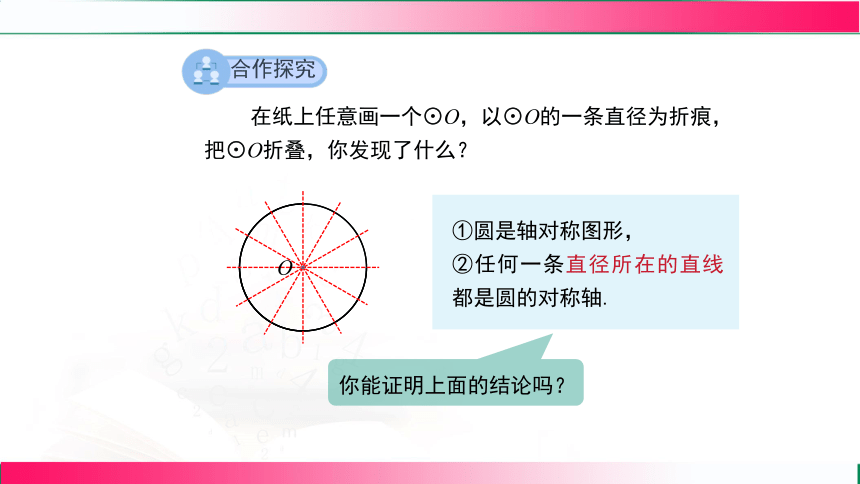
在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O折叠,你发现了什么?
O
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
合作探究
你能证明上面的结论吗?
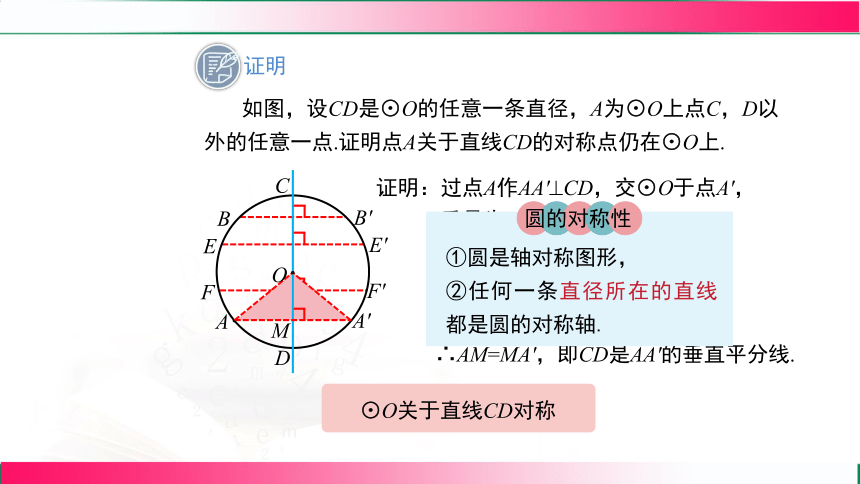
证明:过点A作AA' CD,交⊙O于点A',
垂足为M,连接OA,OA'
在△OAA'中,∵OA OA'
∴△OAA'是等腰三角形
又∵AA' CD
∴AM=MA',即CD是AA'的垂直平分线.
F
F'
E
E'
B
B'
证明
如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.证明点A关于直线CD的对称点仍在⊙O上.
C
D
A
A'
M
O
⊙O关于直线CD对称
圆的对称性
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
如图,在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点,连接AB,得弦AB,这时直径CD与弦AB有怎样的位置关系?
O
合作探究
C
D
A
B
E
猜想
CD AB
△AOB是等腰三角形
AE EB
三线合一
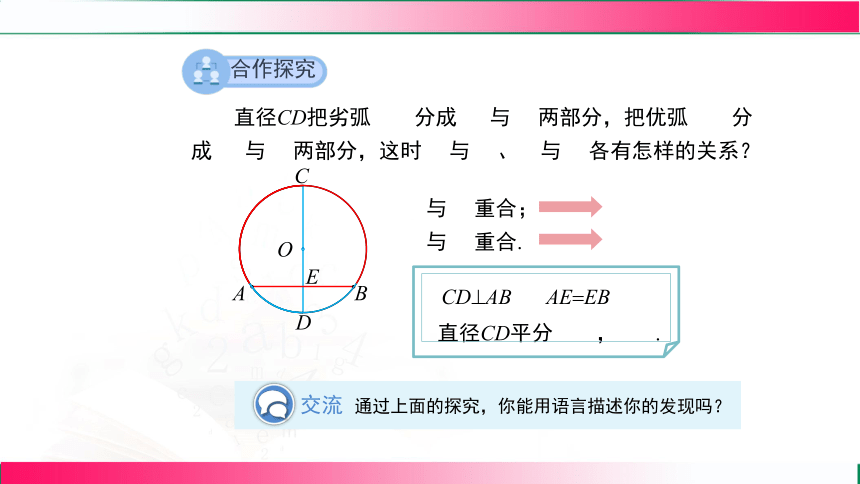
直径CD平分 , .
CD AB
AE EB
合作探究
O
C
D
A
B
E
直径CD把劣弧 分成 与 两部分,把优弧 分成 与 两部分,这时 与 、 与 各有怎样的关系?
与 重合;
与 重合.
通过上面的探究,你能用语言描述你的发现吗?
交流
题设:
①CD是⊙O直径
②CD AB
①直径
②垂直于弦
E
C
O
A
B
D
垂径定理:
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
结论:
①平分弦
②平分弦所对的两条弧
①AE BE
② ,
归纳
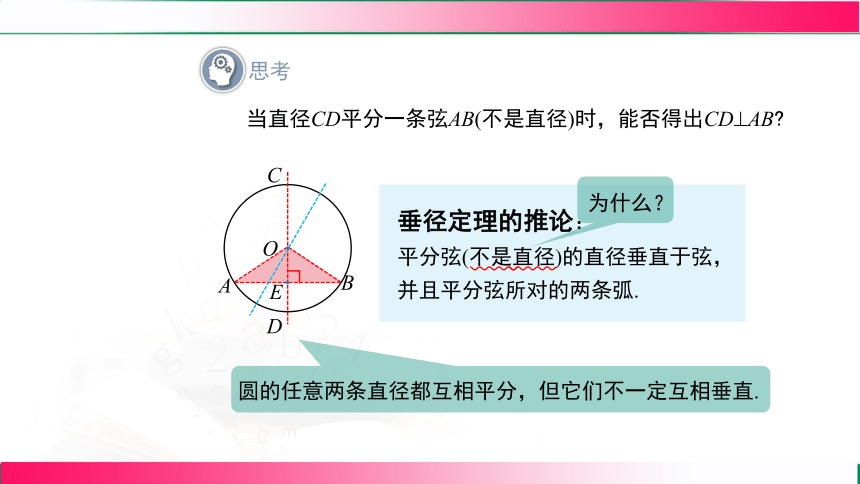
思考
当直径CD平分一条弦AB(不是直径)时,能否得出CD AB
O
A
B
C
D
E
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
为什么?
圆的任意两条直径都互相平分,但它们不一定互相垂直.
典型例题
例1:如图,⊙O的半径为5 cm,弦AB为6 cm,求圆心O到弦AB的距离.
O
A
B
E
解:连接OA,过圆心O做OE AB,垂足为E.
AE EB
AB
6
3 (cm)
又∵OA 5 cm
∴在Rt△OEA中,有
OE
4 (cm)
即圆心O到弦AB的距离是4 cm.
圆心到弦的距离叫做弦心距.
B
A
O
D
C
R
典型例题
例2:赵州桥建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,求赵州桥桥拱所在圆的半径(精确到0.1 m).
37.4 m
7.2 m
解:过桥拱所在圆的圆心O作AB的垂线,交 于点C,交AB于点D,则CD 7.2 m.
由垂径定理,得
AD
AB
37.4
18.7 (m)
设⊙O的半径为R m,在Rt△AOD中,AO R,OD R 7.2,AD 18.7.
由勾股定理得:AO2 OD2 AD2,
∴R2 (R 7.2)2 18.72
答:赵州桥的桥拱所在圆的半径约为27.9m.
解得:R 27.9.
返回
1.下列说法中,不正确的是( )
A.圆是轴对称图形
B.圆的任意一条直径所在的直线都是圆的对称轴
C.圆的任意一条直径都是圆的对称轴
D.经过圆心的任意直线都是圆的对称轴
C
2.[2024·东莞一模]如图,在⊙O中,OD⊥AB,半径OD=10,OC=6,则弦AB=( )
A.8
B.12
C.14
D.16
D
返回
返回
A
3.[2024·杭州萧山区模拟]如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE=( )
A.8 cm
B.5 cm
C.3 cm
D.2 cm
4.如图,AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是________度.
48
返回
返回
返回
6.江南水乡苏州现存100多座石拱桥.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为________m.
8
C
返回
返回
C
9.下列说法:①垂直于弦的直径平分弦;②平分弦的直径垂直于弦;③平分弦所对的一条弧的直径不一定平分另一条弧;④平分任意一条弦所对的两条弧的弦一定是直径.其中正确的是________.(填序号)
①④
简单计算
通常添加半径做辅助线,构造直角三角形,结合勾股定理进行计算或证明.
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
垂径定理
布置作业
教科书第25页
习题24.2第3、8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
24.2.2垂径分弦
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.探索圆的对称性,进而得到垂径定理及其推论;
2.能利用垂径定理及其推论解决相关证明、计算及实际问题;
3.经历探索垂径定理及其推论的过程,发展推理能力,让学生领会数学的严谨性,培养学生实事求是的科学态度;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O折叠,你发现了什么?
O
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
合作探究
你能证明上面的结论吗?
证明:过点A作AA' CD,交⊙O于点A',
垂足为M,连接OA,OA'
在△OAA'中,∵OA OA'
∴△OAA'是等腰三角形
又∵AA' CD
∴AM=MA',即CD是AA'的垂直平分线.
F
F'
E
E'
B
B'
证明
如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.证明点A关于直线CD的对称点仍在⊙O上.
C
D
A
A'
M
O
⊙O关于直线CD对称
圆的对称性
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
如图,在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点,连接AB,得弦AB,这时直径CD与弦AB有怎样的位置关系?
O
合作探究
C
D
A
B
E
猜想
CD AB
△AOB是等腰三角形
AE EB
三线合一
直径CD平分 , .
CD AB
AE EB
合作探究
O
C
D
A
B
E
直径CD把劣弧 分成 与 两部分,把优弧 分成 与 两部分,这时 与 、 与 各有怎样的关系?
与 重合;
与 重合.
通过上面的探究,你能用语言描述你的发现吗?
交流
题设:
①CD是⊙O直径
②CD AB
①直径
②垂直于弦
E
C
O
A
B
D
垂径定理:
垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
结论:
①平分弦
②平分弦所对的两条弧
①AE BE
② ,
归纳
思考
当直径CD平分一条弦AB(不是直径)时,能否得出CD AB
O
A
B
C
D
E
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
为什么?
圆的任意两条直径都互相平分,但它们不一定互相垂直.
典型例题
例1:如图,⊙O的半径为5 cm,弦AB为6 cm,求圆心O到弦AB的距离.
O
A
B
E
解:连接OA,过圆心O做OE AB,垂足为E.
AE EB
AB
6
3 (cm)
又∵OA 5 cm
∴在Rt△OEA中,有
OE
4 (cm)
即圆心O到弦AB的距离是4 cm.
圆心到弦的距离叫做弦心距.
B
A
O
D
C
R
典型例题
例2:赵州桥建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,求赵州桥桥拱所在圆的半径(精确到0.1 m).
37.4 m
7.2 m
解:过桥拱所在圆的圆心O作AB的垂线,交 于点C,交AB于点D,则CD 7.2 m.
由垂径定理,得
AD
AB
37.4
18.7 (m)
设⊙O的半径为R m,在Rt△AOD中,AO R,OD R 7.2,AD 18.7.
由勾股定理得:AO2 OD2 AD2,
∴R2 (R 7.2)2 18.72
答:赵州桥的桥拱所在圆的半径约为27.9m.
解得:R 27.9.
返回
1.下列说法中,不正确的是( )
A.圆是轴对称图形
B.圆的任意一条直径所在的直线都是圆的对称轴
C.圆的任意一条直径都是圆的对称轴
D.经过圆心的任意直线都是圆的对称轴
C
2.[2024·东莞一模]如图,在⊙O中,OD⊥AB,半径OD=10,OC=6,则弦AB=( )
A.8
B.12
C.14
D.16
D
返回
返回
A
3.[2024·杭州萧山区模拟]如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE=( )
A.8 cm
B.5 cm
C.3 cm
D.2 cm
4.如图,AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是________度.
48
返回
返回
返回
6.江南水乡苏州现存100多座石拱桥.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径OC为5 m,则水面宽AB为________m.
8
C
返回
返回
C
9.下列说法:①垂直于弦的直径平分弦;②平分弦的直径垂直于弦;③平分弦所对的一条弧的直径不一定平分另一条弧;④平分任意一条弦所对的两条弧的弦一定是直径.其中正确的是________.(填序号)
①④
简单计算
通常添加半径做辅助线,构造直角三角形,结合勾股定理进行计算或证明.
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
垂径定理
布置作业
教科书第25页
习题24.2第3、8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
谢谢观看!
