24.2.3圆心角、弧、弦、弦心距间关系 课件(共27张PPT)
文档属性
| 名称 | 24.2.3圆心角、弧、弦、弦心距间关系 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:27:16 | ||
图片预览






文档简介
(共27张PPT)
24.2.3圆心角、弧、弦、
弦心距间关系
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
2.掌握在同圆或等圆中,圆心角与其所对的弧、弦、弦心距之间的关系,并能运用此关系进行相关的证明和计算;
3.在探索圆心角、弧、弦、弦心距的关系的过程中,学会运用转化的数学思想解决问题;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
O
在两张透明纸上,分别作半径相等的⊙O和⊙O',把两张纸叠在一起,使⊙O和⊙O'重合,用图钉钉住圆心将上面一个圆旋转180°,两个圆还能重合吗?
合作探究
O'
对称中心为圆心.
圆是中心对称图形,
完全重合
180°
在两张透明纸上,分别作半径相等的⊙O和⊙O',把两张纸叠在一起,使⊙O和⊙O'重合,用图钉钉住圆心将上面一个圆旋转任意一个角度,两个圆还能重合吗?
合作探究
(O')
O
30°
60°
120°
210°
旋转中心为圆心.
圆不仅是中心对称图形,还是旋转对称图形,
把圆绕圆心旋转任意一个角度,两个圆仍然完全重合.
观察下面几个角的顶点,有什么共同特征?
思考
O
A
B
O
C
D
O
E
F
我们把顶点在圆心的角叫做圆心角.
探究
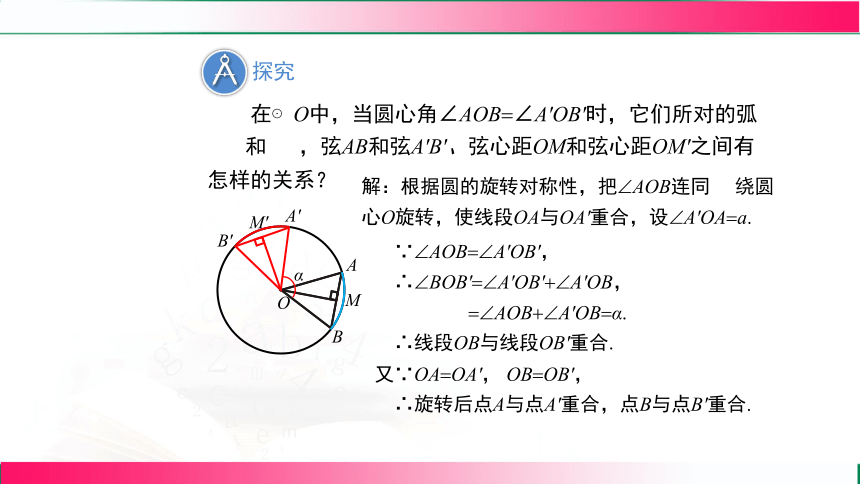
∵ AOB A'OB',
∴ BOB' A'OB' A'OB,
AOB A'OB α.
∴线段OB与线段OB'重合.
又∵OA OA', OB OB',
∴旋转后点A与点A'重合,点B与点B'重合.
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和弦A'B'、弦心距OM和弦心距OM'之间有怎样的关系?
解:根据圆的旋转对称性,把 AOB连同 绕圆心O旋转,使线段OA与OA'重合,设 A'OA a.
O
A'
B'
A
B
M
M'
α
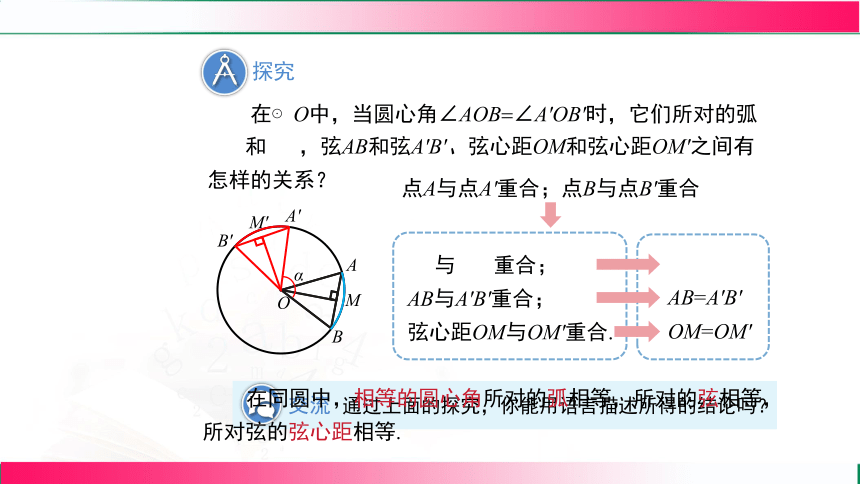
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和弦A'B'、弦心距OM和弦心距OM'之间有怎样的关系?
O
A'
B'
A
B
M
M'
α
与 重合;
AB与A'B'重合;
弦心距OM与OM'重合.
点A与点A'重合;点B与点B'重合
AB=A'B'
OM=OM'
通过上面的探究,你能用语言描述所得的结论吗?
交流
探究
在同圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
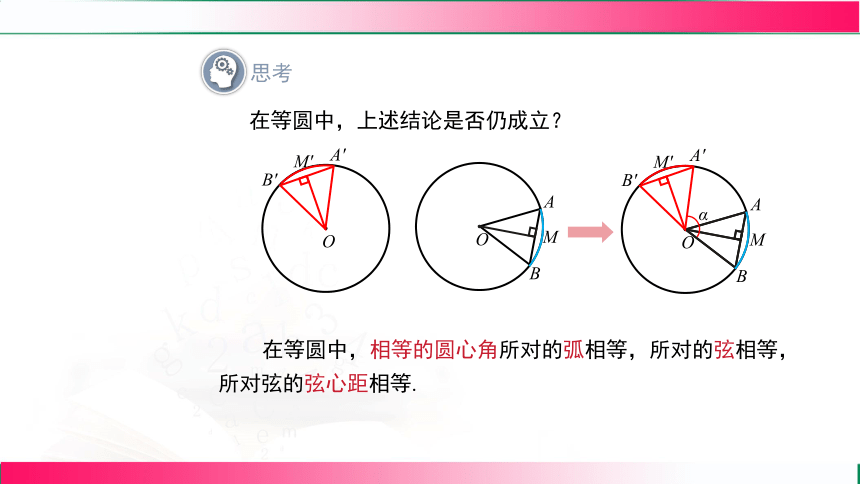
在等圆中,上述结论是否仍成立?
O
A'
B'
M'
A
B
M
O
O
A'
B'
A
B
M
M'
α
思考
在等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
归纳
定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
O
A'
B'
A
B
M
M'
∠AOB ∠A'OB'
AB=A'B'
OM=OM'
典型例题
例1:如图,等边三角形 ABC 的三个顶点都在☉O上.
求证: AOB BOC COA 120°.
A
B
C
O
证明:连接OA,OB,OC.
∵AB BC CA,
∴ AOB BOC COA
360° 120°.
圆心角相等
弦相等
分析:
圆心角、弧、弦、弦心距的灵活转化是解决圆相关问题的重要法宝.
K
K'
典型例题
例2:已知:如图,点O是∠FAD平分线上的一点,☉O分别交∠FAD的两边于点C,D和点E,F.
求证:CD=EF.
证明:过点O作OK CD,OK' EF,垂足分别为K,K'.
∵OK OK',(角平分线性质)
∴CD EF.
O
A
D
E
F
C
弦相等
弦心距相等
分析:
典型例题
例3:如图,AB,CD是☉O的两条直径,CE为☉O的弦,且CE//AB, 为40°,求 BOD的度数.
O
C
E
B
A
D
解:连接OE.
∵ 为40°,
∴ COE 40°,
∵OC OE,
∴ C 70°.
∵CE//AB,
∴ AOD C 70°.
∴ BOD 180° 70° 110°.
返回
1.[2024·泉州五中期中]下列图形中的角是圆心角的是( )
B
返回
D
返回
3.[2024·上海静安区二模]对于命题:①如果两条弧相等,那么它们所对的圆心角相等;②如果两个圆心角相等,那么它们所对的弧相等.下列判断正确的是( )
A.①是真命题,②是假命题
B.①是假命题,②是真命题
C.①、②都是真命题
D.①、②都是假命题
A
【答案】C
返回
返回
5.如图,点A,B分别为半圆O上的三等分点,如果⊙O的半径为8 cm,那么弦AB=________ cm.
8
①②③
返回
7.[2024·南宁一模]如图,当一个摆钟的钟摆OA从最左侧处摆到最右侧OB处时,摆角∠AOB=2α,点C是弧AB的中点,连接OC交AB于点D,若OA=20 cm,则AB的长为________cm.(结果用到α相关的三角函数)
40sin α
圆的对称性
圆不仅是中心对称图形,还是旋转对称图形,旋转中心是圆心.
弧的度数
圆心角的度数和它所对的弧的度数相等.
圆心角、弧、弦、弦心距间的关系
定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
圆心角、弧、弦、弦心距间关系
推论 在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等.
教科书第25页
练习第6、7题
谢谢观看!
24.2.3圆心角、弧、弦、
弦心距间关系
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解圆心角的概念和圆的旋转不变性,会辨析圆心角;
2.掌握在同圆或等圆中,圆心角与其所对的弧、弦、弦心距之间的关系,并能运用此关系进行相关的证明和计算;
3.在探索圆心角、弧、弦、弦心距的关系的过程中,学会运用转化的数学思想解决问题;
实验操作:给每个小组发放三角形纸片、方格纸、图钉等材料。让学生将三角形纸片固定在方格纸上的某一点(作为旋转中心),然后将三角形绕旋转中心顺时针旋转 90°,观察三角形旋转前后的位置变化,并在方格纸上画出旋转后的图形。
引导学生观察旋转前后的三角形,思考以下问题:
旋转前后三角形的形状和大小有没有改变?
对应点(如三角形的顶点)到旋转中心的距离有什么关系?
对应点与旋转中心所连线段的夹角与旋转角有什么关系?
小组讨论并汇报结果,教师进行总结:
图形旋转的性质:旋转前后图形的形状和大小不变。
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
利用多媒体课件再次展示图形旋转的过程,从动态的角度进一步验证这些性质,加深学生的理解。
(四)在方格纸上画出旋转后的图形(15 分钟)
以在方格纸上将一个简单图形(如直角三角形)绕某一顶点顺时针旋转 90° 为例,教师进行详细的示范讲解。
首先确定旋转中心(直角三角形的一个顶点)。
然后找到三角形的另外两个顶点,分别将这两示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。个顶点与旋转中心相连。
根据旋转方向(顺时针)和旋转角度(90°),通过数方格的方法确定这两个顶点旋转后的位置。
最后将旋转后的三个顶点依次连接起来,得到旋转后的三角形。
让学生模仿教师的方法,在方格纸上练习将一个简单图形绕给定旋转中心旋转 90°,教师巡视指导,及时纠正学生在画图过程中出现的问题。
提高难度,让学生尝试在方格纸上画出简单图形绕给定旋转中心旋转 180° 后的图形,进一步巩固学生的画图技能。
组织学生进行小组交流,展示各自画出的旋转后的图形,互相评价并交流画图的经验和技巧。
(五)巩固练习(10 分钟)
出示一些关于图形旋转要素、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些方格纸上的图形旋转问题,要求学生画出图形绕指定旋转中心旋转一定角度后的图形,然后同桌之间互相检查批改。
给出一些生活中的实际问题,如设计一个旋转图案、根据旋转后的图形推测旋转前的图形等,让学生分组讨论并解决问题,培养学生运用所学知识解决实际问题的能力。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括图形旋转的概念、三要素、性质以及在方格纸上画旋转后图形的方法。
强调图形旋转在生活中的广泛应用,鼓励学生在日常生活中多观察、多发现图形旋转的现象,运用所学的数学知识去分析和解决问题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
O
在两张透明纸上,分别作半径相等的⊙O和⊙O',把两张纸叠在一起,使⊙O和⊙O'重合,用图钉钉住圆心将上面一个圆旋转180°,两个圆还能重合吗?
合作探究
O'
对称中心为圆心.
圆是中心对称图形,
完全重合
180°
在两张透明纸上,分别作半径相等的⊙O和⊙O',把两张纸叠在一起,使⊙O和⊙O'重合,用图钉钉住圆心将上面一个圆旋转任意一个角度,两个圆还能重合吗?
合作探究
(O')
O
30°
60°
120°
210°
旋转中心为圆心.
圆不仅是中心对称图形,还是旋转对称图形,
把圆绕圆心旋转任意一个角度,两个圆仍然完全重合.
观察下面几个角的顶点,有什么共同特征?
思考
O
A
B
O
C
D
O
E
F
我们把顶点在圆心的角叫做圆心角.
探究
∵ AOB A'OB',
∴ BOB' A'OB' A'OB,
AOB A'OB α.
∴线段OB与线段OB'重合.
又∵OA OA', OB OB',
∴旋转后点A与点A'重合,点B与点B'重合.
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和弦A'B'、弦心距OM和弦心距OM'之间有怎样的关系?
解:根据圆的旋转对称性,把 AOB连同 绕圆心O旋转,使线段OA与OA'重合,设 A'OA a.
O
A'
B'
A
B
M
M'
α
在⊙O中,当圆心角∠AOB ∠A'OB'时,它们所对的弧
和 ,弦AB和弦A'B'、弦心距OM和弦心距OM'之间有怎样的关系?
O
A'
B'
A
B
M
M'
α
与 重合;
AB与A'B'重合;
弦心距OM与OM'重合.
点A与点A'重合;点B与点B'重合
AB=A'B'
OM=OM'
通过上面的探究,你能用语言描述所得的结论吗?
交流
探究
在同圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
在等圆中,上述结论是否仍成立?
O
A'
B'
M'
A
B
M
O
O
A'
B'
A
B
M
M'
α
思考
在等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
归纳
定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
O
A'
B'
A
B
M
M'
∠AOB ∠A'OB'
AB=A'B'
OM=OM'
典型例题
例1:如图,等边三角形 ABC 的三个顶点都在☉O上.
求证: AOB BOC COA 120°.
A
B
C
O
证明:连接OA,OB,OC.
∵AB BC CA,
∴ AOB BOC COA
360° 120°.
圆心角相等
弦相等
分析:
圆心角、弧、弦、弦心距的灵活转化是解决圆相关问题的重要法宝.
K
K'
典型例题
例2:已知:如图,点O是∠FAD平分线上的一点,☉O分别交∠FAD的两边于点C,D和点E,F.
求证:CD=EF.
证明:过点O作OK CD,OK' EF,垂足分别为K,K'.
∵OK OK',(角平分线性质)
∴CD EF.
O
A
D
E
F
C
弦相等
弦心距相等
分析:
典型例题
例3:如图,AB,CD是☉O的两条直径,CE为☉O的弦,且CE//AB, 为40°,求 BOD的度数.
O
C
E
B
A
D
解:连接OE.
∵ 为40°,
∴ COE 40°,
∵OC OE,
∴ C 70°.
∵CE//AB,
∴ AOD C 70°.
∴ BOD 180° 70° 110°.
返回
1.[2024·泉州五中期中]下列图形中的角是圆心角的是( )
B
返回
D
返回
3.[2024·上海静安区二模]对于命题:①如果两条弧相等,那么它们所对的圆心角相等;②如果两个圆心角相等,那么它们所对的弧相等.下列判断正确的是( )
A.①是真命题,②是假命题
B.①是假命题,②是真命题
C.①、②都是真命题
D.①、②都是假命题
A
【答案】C
返回
返回
5.如图,点A,B分别为半圆O上的三等分点,如果⊙O的半径为8 cm,那么弦AB=________ cm.
8
①②③
返回
7.[2024·南宁一模]如图,当一个摆钟的钟摆OA从最左侧处摆到最右侧OB处时,摆角∠AOB=2α,点C是弧AB的中点,连接OC交AB于点D,若OA=20 cm,则AB的长为________cm.(结果用到α相关的三角函数)
40sin α
圆的对称性
圆不仅是中心对称图形,还是旋转对称图形,旋转中心是圆心.
弧的度数
圆心角的度数和它所对的弧的度数相等.
圆心角、弧、弦、弦心距间的关系
定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
圆心角、弧、弦、弦心距间关系
推论 在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等.
教科书第25页
练习第6、7题
谢谢观看!
