24.3.1圆周角定理及其推论 课件(共31张PPT)
文档属性
| 名称 | 24.3.1圆周角定理及其推论 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:31:18 | ||
图片预览






文档简介
(共31张PPT)
24.3.1圆周角定理及其推论
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.了解圆周角的概念;
2.掌握圆周角定理及其推论,并会熟练运用它们解决问题;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
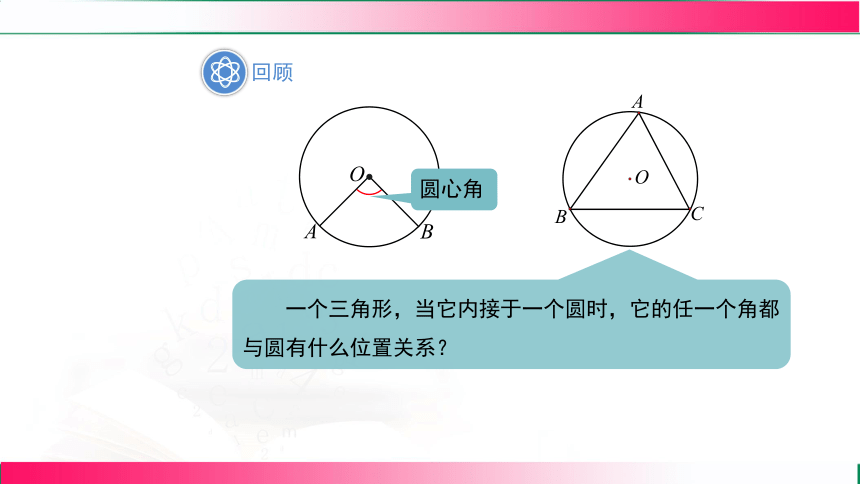
回顾
A
B
O
圆心角
A
B
C
O
一个三角形,当它内接于一个圆时,它的任一个角都与圆有什么位置关系?
观察思考
如图,△ABC内接于⊙O,观察图中的 A,它有什么特点?
A
B
C
O
1.顶点在圆上;
2.角的两边与圆各另有一个公共点.
顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
缺一不可
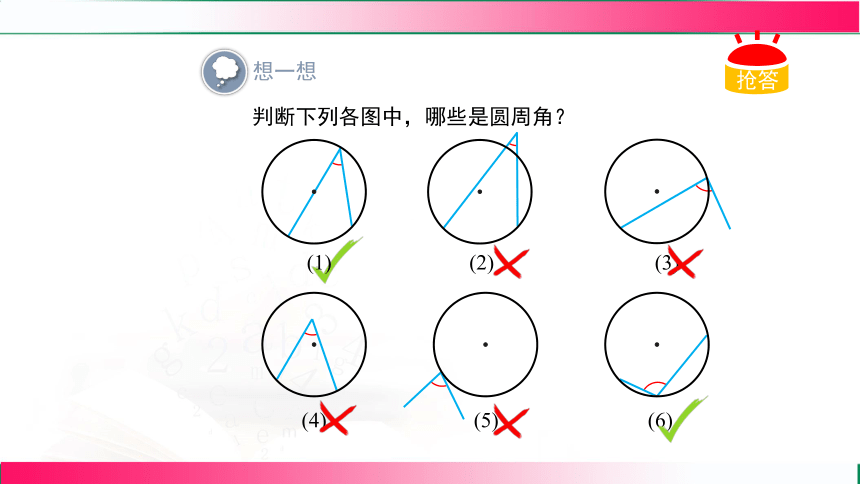
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
抢答
A
B
C
O
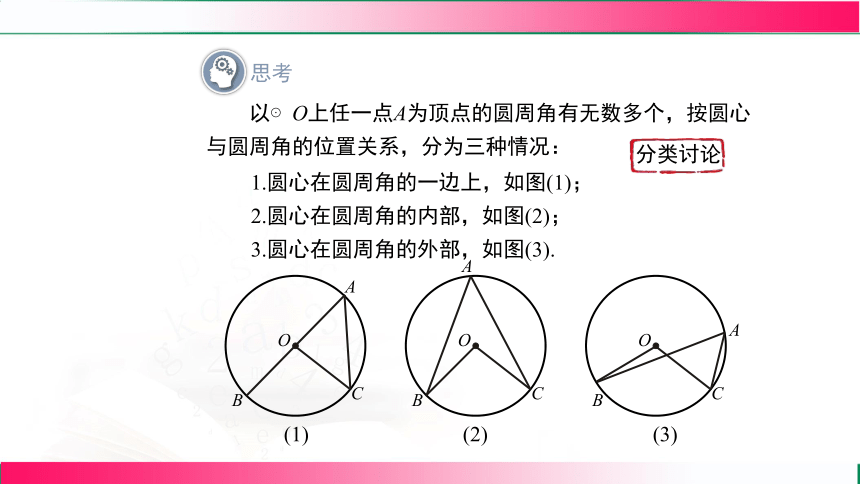
思考
如图,△ABC是⊙O的任一内接三角形. BAC和∠BOC的大小有什么关系吗?
100°
50°
猜想
一条弧所对的圆周角等于它所对圆心角的一半.
你能证明这个猜想吗
思考
以⊙O上任一点A为顶点的圆周角有无数多个,按圆心与圆周角的位置关系,分为三种情况:
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
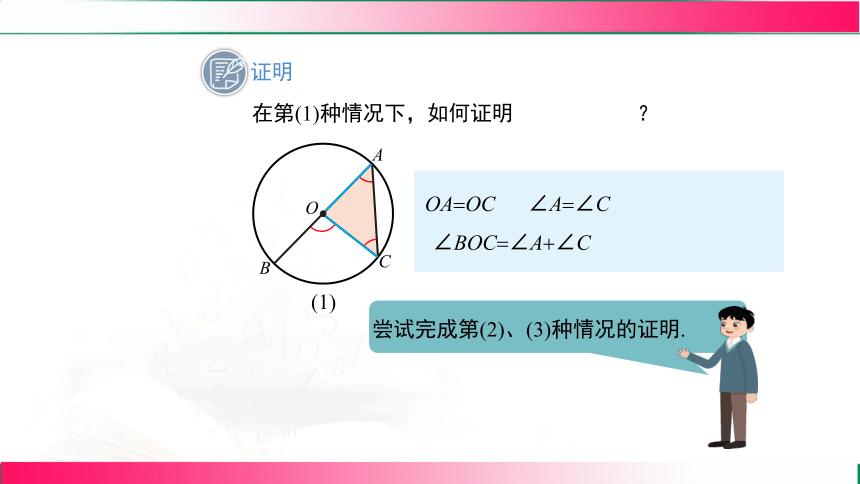
证明
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
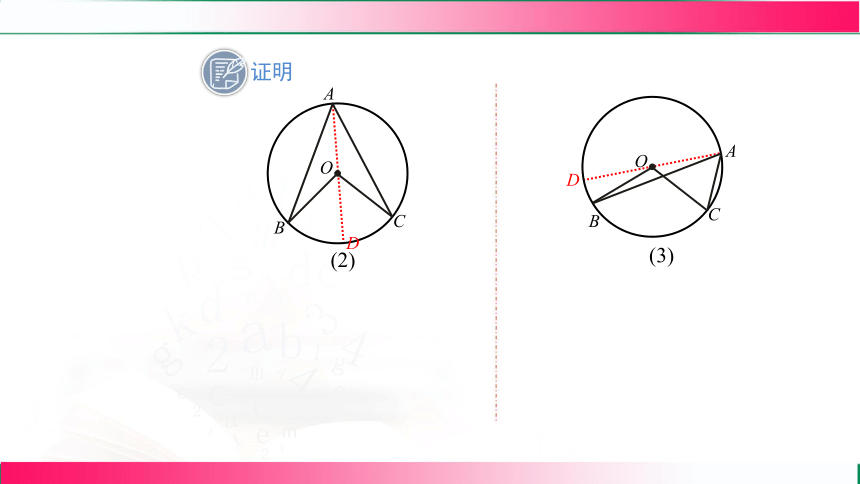
证明
A
B
O
C
(2)
D
A
B
O
C
(3)
D
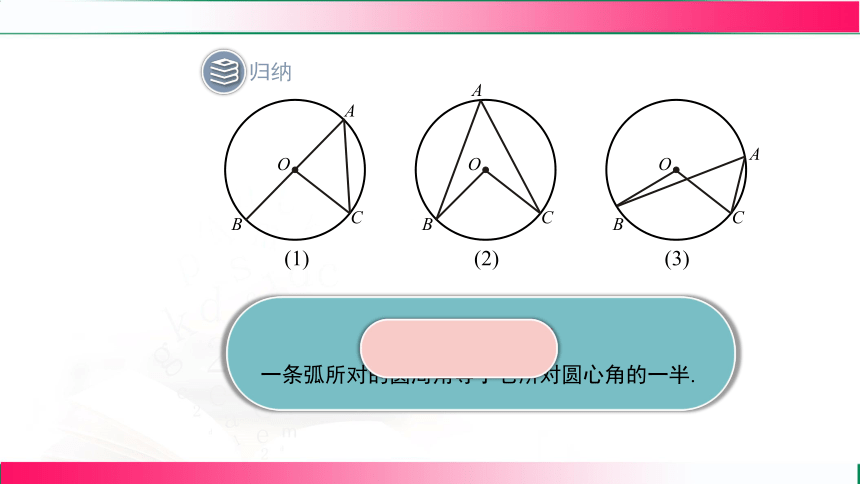
归纳
圆周角定理
一条弧所对的圆周角等于它所对圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
O
∠AC1B ∠AC2B ∠AC3B
C2
C1
C3
∠AC1B ∠AC2B ∠AC3B
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
在同圆或等圆中,同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
思考
反过来,在同圆或等圆中,如果圆周角相等,那它们所对的弧相等吗?
在同圆或等圆中,相等的圆周角所对的弧也相等.
B
A
O
D
C
ADC BAD
AOC BOD
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等.
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
归纳
分析:
典型例题
例1 如图,AB为⊙O的直径,弦CD交AB于点P, ACD 60°, ADC 70°. 求∠APC的度数.
O
A
D
C
P
B
解:连接BC,则 ACB 90°,
DCB ACB ACD 90° 60° 30°.
又∵ BAD ∠DCB 30°,
∴ APC BAD ADC 30° 70° 100°.
APC BAD ADC
70°
ACB ACD
BCD
90°
60°
返回
1.下列各图中,∠BAC为圆周角的是( )
D
2.[2024·湖南]如图,AB,AC为⊙O的两条弦,连接OB,OC,若∠A=45°,则∠BOC的度数为( )
A.60°
B.75°
C.90°
D.135°
返回
C
返回
D
3.如图,AB是⊙O的直径,∠E=35°,则∠BOD=( )
A.80°
B.100°
C.120°
D.110°
4.[2024·温州模拟]如图,△ABC内接于⊙O,AB=AC,∠B=70°,则∠OCB=( )
A.40°
B.50°
C.60°
D.65°
返回
【答案】 B
5.[2023·枣庄]如图,在⊙O中,弦AB,CD相交于点P.若∠A=48°,∠APD=80°,则∠B的大小为( )
A.32°
B.42°
C.52°
D.62°
返回
A
返回
6.如图,△ABC内接于⊙O,AD是⊙O的直径.若∠B=20°,则∠CAD的度数是( )
A.60°
B.65°
C.70°
D.75°
C
7.如图,点A,B,C,D在⊙O上,∠CAD=30°,∠ABD=50°,则∠ADC=________.
100°
【点拨】∵∠ABD=50°,
∴∠ACD=∠ABD=50°.
又∵∠CAD=30°,
∴∠ADC=180°-∠CAD-∠ACD=180°-30°-50°=100°.
返回
【点拨】如图,延长AO交⊙O于点E,连接DE,
∵AE是直径,∴∠ADE=90°.
∵OA与OB互相垂直,
∴∠AOC=90°=∠ADE.
返回
9.有一题目:“已知点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆⊙O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就是65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
A
返回
圆周角
顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等.相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆周角
教科书第31页
习题24.3第1、2题
谢谢观看!
24.3.1圆周角定理及其推论
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.了解圆周角的概念;
2.掌握圆周角定理及其推论,并会熟练运用它们解决问题;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
回顾
A
B
O
圆心角
A
B
C
O
一个三角形,当它内接于一个圆时,它的任一个角都与圆有什么位置关系?
观察思考
如图,△ABC内接于⊙O,观察图中的 A,它有什么特点?
A
B
C
O
1.顶点在圆上;
2.角的两边与圆各另有一个公共点.
顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
缺一不可
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
抢答
A
B
C
O
思考
如图,△ABC是⊙O的任一内接三角形. BAC和∠BOC的大小有什么关系吗?
100°
50°
猜想
一条弧所对的圆周角等于它所对圆心角的一半.
你能证明这个猜想吗
思考
以⊙O上任一点A为顶点的圆周角有无数多个,按圆心与圆周角的位置关系,分为三种情况:
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
证明
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
证明
A
B
O
C
(2)
D
A
B
O
C
(3)
D
归纳
圆周角定理
一条弧所对的圆周角等于它所对圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
O
∠AC1B ∠AC2B ∠AC3B
C2
C1
C3
∠AC1B ∠AC2B ∠AC3B
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
在同圆或等圆中,同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
思考
反过来,在同圆或等圆中,如果圆周角相等,那它们所对的弧相等吗?
在同圆或等圆中,相等的圆周角所对的弧也相等.
B
A
O
D
C
ADC BAD
AOC BOD
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等.
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,
相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
归纳
分析:
典型例题
例1 如图,AB为⊙O的直径,弦CD交AB于点P, ACD 60°, ADC 70°. 求∠APC的度数.
O
A
D
C
P
B
解:连接BC,则 ACB 90°,
DCB ACB ACD 90° 60° 30°.
又∵ BAD ∠DCB 30°,
∴ APC BAD ADC 30° 70° 100°.
APC BAD ADC
70°
ACB ACD
BCD
90°
60°
返回
1.下列各图中,∠BAC为圆周角的是( )
D
2.[2024·湖南]如图,AB,AC为⊙O的两条弦,连接OB,OC,若∠A=45°,则∠BOC的度数为( )
A.60°
B.75°
C.90°
D.135°
返回
C
返回
D
3.如图,AB是⊙O的直径,∠E=35°,则∠BOD=( )
A.80°
B.100°
C.120°
D.110°
4.[2024·温州模拟]如图,△ABC内接于⊙O,AB=AC,∠B=70°,则∠OCB=( )
A.40°
B.50°
C.60°
D.65°
返回
【答案】 B
5.[2023·枣庄]如图,在⊙O中,弦AB,CD相交于点P.若∠A=48°,∠APD=80°,则∠B的大小为( )
A.32°
B.42°
C.52°
D.62°
返回
A
返回
6.如图,△ABC内接于⊙O,AD是⊙O的直径.若∠B=20°,则∠CAD的度数是( )
A.60°
B.65°
C.70°
D.75°
C
7.如图,点A,B,C,D在⊙O上,∠CAD=30°,∠ABD=50°,则∠ADC=________.
100°
【点拨】∵∠ABD=50°,
∴∠ACD=∠ABD=50°.
又∵∠CAD=30°,
∴∠ADC=180°-∠CAD-∠ACD=180°-30°-50°=100°.
返回
【点拨】如图,延长AO交⊙O于点E,连接DE,
∵AE是直径,∴∠ADE=90°.
∵OA与OB互相垂直,
∴∠AOC=90°=∠ADE.
返回
9.有一题目:“已知点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆⊙O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说的对,且∠A的另一个值是115°
B.淇淇说的不对,∠A就是65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
A
返回
圆周角
顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半.
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等.相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆周角
教科书第31页
习题24.3第1、2题
谢谢观看!
