24.4.3切线长定理 课件(共29张PPT)
文档属性
| 名称 | 24.4.3切线长定理 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:39:27 | ||
图片预览




文档简介
(共29张PPT)
24.4.3切线长定理
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解切线长的定义及切线长定理;
2.学会运用切线长定理进行计算与证明;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察悠悠球转动时的内部结构,从中你能抽象出什么样的数学图形?
观察思考
球的整体和中心轴可分别抽象成圆形
被拉直的线绳可抽象成线段
这些图形有怎样的位置关系?
相切
复习回顾
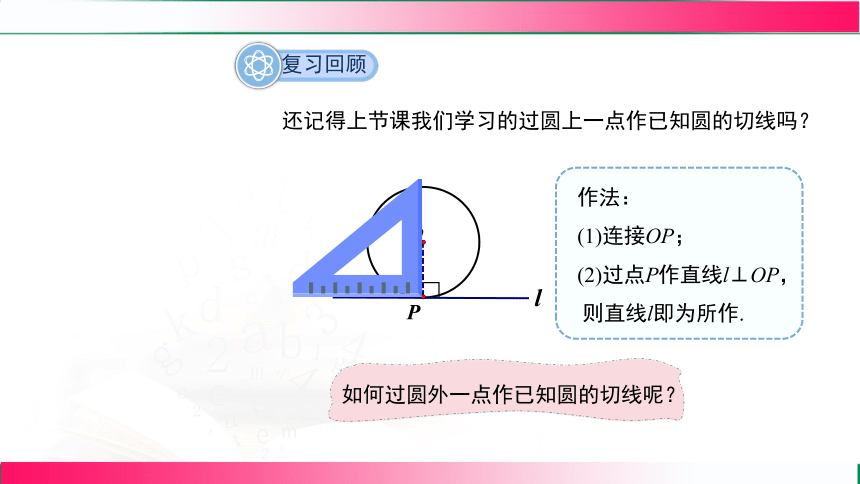
还记得上节课我们学习的过圆上一点作已知圆的切线吗?
∟
o
P
l
作法:
(1)连接OP;
(2)过点P作直线l⊥OP,
则直线l即为所作.
如何过圆外一点作已知圆的切线呢?
O.
P
合作探究
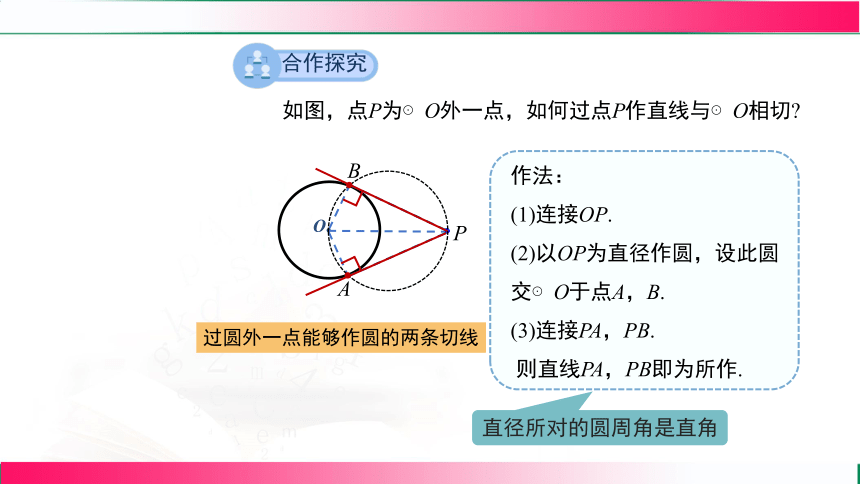
如图,点P为⊙O外一点,如何过点P作直线与⊙O相切
B
A
过圆外一点能够作圆的两条切线
作法:
(1)连接OP.
(2)以OP为直径作圆,设此圆
交⊙O于点A,B.
(3)连接PA,PB.
则直线PA,PB即为所作.
直径所对的圆周角是直角
O.
P
B
A
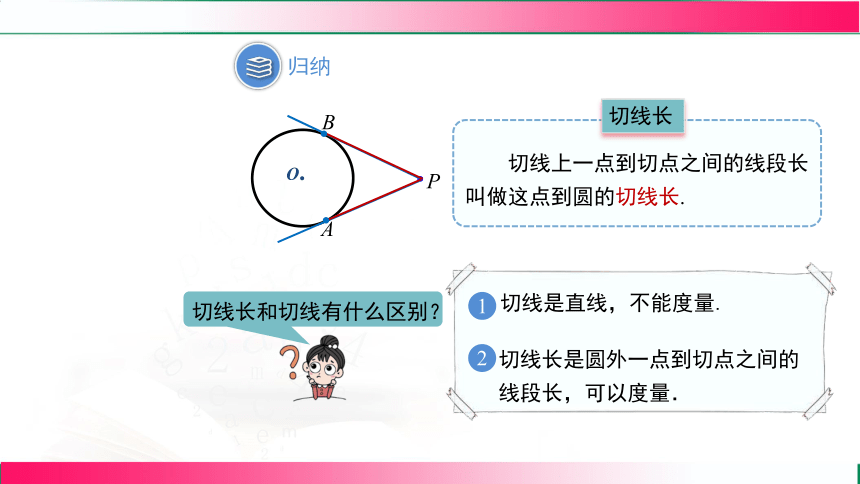
切线长
切线上一点到切点之间的线段长叫做这点到圆的切线长.
归纳
切线长和切线有什么区别?
切线是直线,不能度量.
切线长是圆外一点到切点之间的线段长,可以度量.
1
2
探究
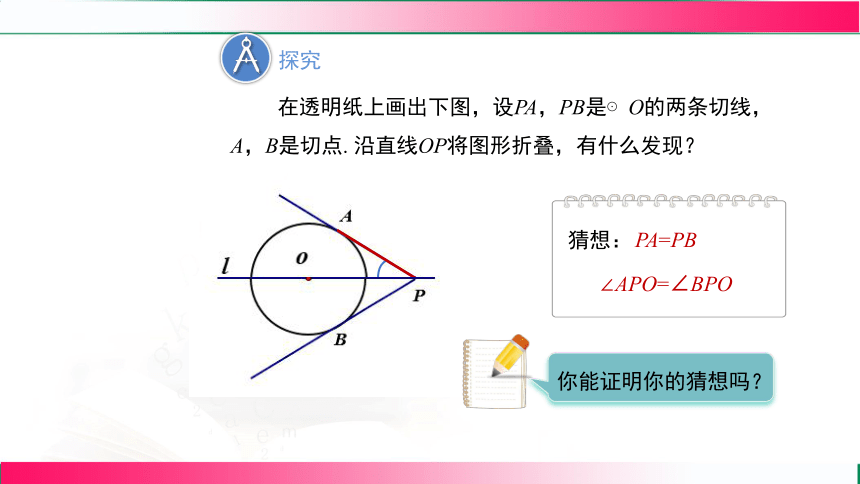
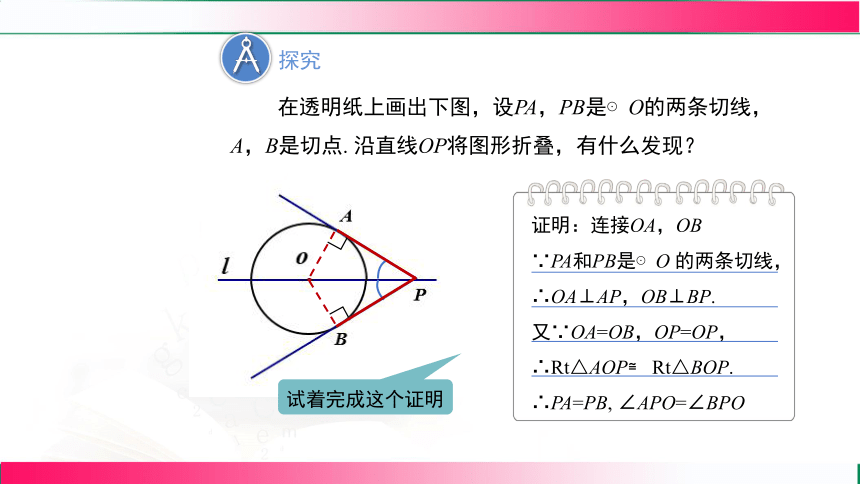
在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点. 沿直线OP将图形折叠,有什么发现?
PA=PB
∠APO=∠BPO
你能证明你的猜想吗?
猜想:
探究
证明:连接OA,OB
∵PA和PB是⊙O 的两条切线,
∴OA⊥AP,OB⊥BP.
又∵OA=OB,OP=OP,
∴Rt△AOP≌ Rt△BOP.
∴PA=PB, ∠APO=∠BPO
∟
∟
在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点. 沿直线OP将图形折叠,有什么发现?
试着完成这个证明
归纳
文字语言
符号语言
过圆外一点作圆的
切线,两条切线长 ,圆心与这一点的连线 两条切线的夹角.
∵PA、PB分别与☉O 相切于点A、B,
∴ PA = PB,
∠OPA=∠OPB.
两条
相等
切线长定理
平分
典型例题
【例】已知:如图,四边形ABCD的边AB、BC、CD、 DA和☉O分别相切于点E,F,G,H.
求证: AB+CD=DA+BC.
证明:∵ AB、BC、CD、 DA都与☉O相切,E,F,G,H是切点,
∴AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH,
即 AB+CD=DA+BC.
A
C
E
D
F
O
B
G
H
转化思想
1.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,则⊙O的半径等于________.
1
返回
2.[2024·淮南七中月考]如图,直线PA,PB,MN分别与⊙O相切于点A,B,D,PA=PB=4 cm,△PMN的周长是________.
8 cm
【点拨】∵直线PA,PB,MN分别与⊙O相切于点A,B,D,∴AM=DM,BN=DN.
∵PA=PB=4 cm,
∴△PMN的周长是PM+PN+MN=PM+PN+DM+DN=(PM+DM)+(PN+DN)=(PM+AM)+(PN+BN)=AP+BP=8 cm.故答案为8 cm.
返回
3.[2024·常州钟楼区月考]如图,PA,PB是⊙O的切线,切点分别是点A和B,AC是⊙O的直径.若∠P=60°,BC=2,则PA的长为________.
【点拨】如图,连接AB.
∵PA,PB是⊙O的切线,切点分别是点A和B,
∴PA⊥AC,PA=PB.∴∠PAC=90°.
∵∠P=60°,∴△PAB为等边三角形.
∴AB=PA,∠PAB=60°.∴∠BAC=30°.
返回
4. 如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( )
A.56°
B.60°
C.68°
D.70°
【点拨】如图,连接AD.
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°.
∵∠BAE+∠BCD=236°,
∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°.
∴∠EAD=56°.
∵EA,ED是⊙O的切线,切点为A,D,
∴EA=ED.∴∠EDA=∠EAD=56°.
∴∠E=180°-∠EDA-∠EAD=180°-56°-56°=68°.
返回
【答案】 C
5.如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB;②OP⊥AB;③四边形OAPB有外接圆;④M是△AOP外接圆的圆心.其中正确说法的个数是( )
A.1
B.2
C.3
D.4
【点拨】∵ PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO, 故①正确.
∴PO⊥AB, 故②正确.
∵ PA,PB是⊙O的两条切线,
∴∠OAP=∠OBP=90°.
∴点A,B在以OP为直径的圆上.
∴四边形OAPB有外接圆,故③正确.
∵只有当∠APO=30°时,OP=2OA,此时PM=OM,
∴M不一定是△AOP外接圆的圆心,故④错误.
故选C.
返回
【答案】 C
6.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
A.28°
B.50°
C.56°
D.62°
【点拨】如图,连接OB.∵OA=OB,
∴∠OAB=∠OBA=28°.∴∠AOB=124°.
∵PA,PB切⊙O于A,B,∴OA⊥PA,OB⊥PB.
∴∠OAP+∠OBP=180°.
∴∠APB+∠AOB=180°.
∴∠APB=56°.故选C.
【答案】 C
返回
切线长:
切线长定理
切线长定理:
切线上一点到切点之间的线段长叫做这点到圆的切线长.
过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角.
教科书第40-41页
习题24.4
第9、10题
谢谢观看!
24.4.3切线长定理
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解切线长的定义及切线长定理;
2.学会运用切线长定理进行计算与证明;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察悠悠球转动时的内部结构,从中你能抽象出什么样的数学图形?
观察思考
球的整体和中心轴可分别抽象成圆形
被拉直的线绳可抽象成线段
这些图形有怎样的位置关系?
相切
复习回顾
还记得上节课我们学习的过圆上一点作已知圆的切线吗?
∟
o
P
l
作法:
(1)连接OP;
(2)过点P作直线l⊥OP,
则直线l即为所作.
如何过圆外一点作已知圆的切线呢?
O.
P
合作探究
如图,点P为⊙O外一点,如何过点P作直线与⊙O相切
B
A
过圆外一点能够作圆的两条切线
作法:
(1)连接OP.
(2)以OP为直径作圆,设此圆
交⊙O于点A,B.
(3)连接PA,PB.
则直线PA,PB即为所作.
直径所对的圆周角是直角
O.
P
B
A
切线长
切线上一点到切点之间的线段长叫做这点到圆的切线长.
归纳
切线长和切线有什么区别?
切线是直线,不能度量.
切线长是圆外一点到切点之间的线段长,可以度量.
1
2
探究
在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点. 沿直线OP将图形折叠,有什么发现?
PA=PB
∠APO=∠BPO
你能证明你的猜想吗?
猜想:
探究
证明:连接OA,OB
∵PA和PB是⊙O 的两条切线,
∴OA⊥AP,OB⊥BP.
又∵OA=OB,OP=OP,
∴Rt△AOP≌ Rt△BOP.
∴PA=PB, ∠APO=∠BPO
∟
∟
在透明纸上画出下图,设PA,PB是⊙O的两条切线,A,B是切点. 沿直线OP将图形折叠,有什么发现?
试着完成这个证明
归纳
文字语言
符号语言
过圆外一点作圆的
切线,两条切线长 ,圆心与这一点的连线 两条切线的夹角.
∵PA、PB分别与☉O 相切于点A、B,
∴ PA = PB,
∠OPA=∠OPB.
两条
相等
切线长定理
平分
典型例题
【例】已知:如图,四边形ABCD的边AB、BC、CD、 DA和☉O分别相切于点E,F,G,H.
求证: AB+CD=DA+BC.
证明:∵ AB、BC、CD、 DA都与☉O相切,E,F,G,H是切点,
∴AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH,
即 AB+CD=DA+BC.
A
C
E
D
F
O
B
G
H
转化思想
1.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=2,则⊙O的半径等于________.
1
返回
2.[2024·淮南七中月考]如图,直线PA,PB,MN分别与⊙O相切于点A,B,D,PA=PB=4 cm,△PMN的周长是________.
8 cm
【点拨】∵直线PA,PB,MN分别与⊙O相切于点A,B,D,∴AM=DM,BN=DN.
∵PA=PB=4 cm,
∴△PMN的周长是PM+PN+MN=PM+PN+DM+DN=(PM+DM)+(PN+DN)=(PM+AM)+(PN+BN)=AP+BP=8 cm.故答案为8 cm.
返回
3.[2024·常州钟楼区月考]如图,PA,PB是⊙O的切线,切点分别是点A和B,AC是⊙O的直径.若∠P=60°,BC=2,则PA的长为________.
【点拨】如图,连接AB.
∵PA,PB是⊙O的切线,切点分别是点A和B,
∴PA⊥AC,PA=PB.∴∠PAC=90°.
∵∠P=60°,∴△PAB为等边三角形.
∴AB=PA,∠PAB=60°.∴∠BAC=30°.
返回
4. 如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( )
A.56°
B.60°
C.68°
D.70°
【点拨】如图,连接AD.
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°.
∵∠BAE+∠BCD=236°,
∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°.
∴∠EAD=56°.
∵EA,ED是⊙O的切线,切点为A,D,
∴EA=ED.∴∠EDA=∠EAD=56°.
∴∠E=180°-∠EDA-∠EAD=180°-56°-56°=68°.
返回
【答案】 C
5.如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB;②OP⊥AB;③四边形OAPB有外接圆;④M是△AOP外接圆的圆心.其中正确说法的个数是( )
A.1
B.2
C.3
D.4
【点拨】∵ PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO, 故①正确.
∴PO⊥AB, 故②正确.
∵ PA,PB是⊙O的两条切线,
∴∠OAP=∠OBP=90°.
∴点A,B在以OP为直径的圆上.
∴四边形OAPB有外接圆,故③正确.
∵只有当∠APO=30°时,OP=2OA,此时PM=OM,
∴M不一定是△AOP外接圆的圆心,故④错误.
故选C.
返回
【答案】 C
6.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
A.28°
B.50°
C.56°
D.62°
【点拨】如图,连接OB.∵OA=OB,
∴∠OAB=∠OBA=28°.∴∠AOB=124°.
∵PA,PB切⊙O于A,B,∴OA⊥PA,OB⊥PB.
∴∠OAP+∠OBP=180°.
∴∠APB+∠AOB=180°.
∴∠APB=56°.故选C.
【答案】 C
返回
切线长:
切线长定理
切线长定理:
切线上一点到切点之间的线段长叫做这点到圆的切线长.
过圆外一点作圆的两条切线,两条切线长相等,圆心与这一点的连线平分两条切线的夹角.
教科书第40-41页
习题24.4
第9、10题
谢谢观看!
