24.6.1正多边形与圆 课件(共29张PPT)
文档属性
| 名称 | 24.6.1正多边形与圆 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:41:19 | ||
图片预览






文档简介
(共29张PPT)
24.6.1正多边形与圆
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解正多边形与圆的关系;
2.能用尺规作出特殊的正多边形,并设计画出各种相关图案;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
(七)布置作业(2 分钟)
完成课本上相关的练习题。
测量家里圆形物体的直径或半径,计算其周长和面积,并记录下来。
五、教学反思
在本节课的教学过程中,通过多种教学方法的运用,学生对圆的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实验探究环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的探究能力和实践操作能力。小组合作学习也促进了学生之间的交流与合作。然而,在教学过程中也存在一些不足之处,如在推导圆的面积公式时,部分学生对转化思想的理解还不够深刻;在解决实际问题时,部分学生不能灵活运用所学知识。在今后的教学中,我将进一步加强对学生的引导,注重知识的形成过程,提高学生的数学思维能力和应用能力。
生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
什么样的多边形叫做正多边形呢?
复习回顾
各边相等、各角也相等的多边形叫做正多边形.
能否从下图中找出正多边形?
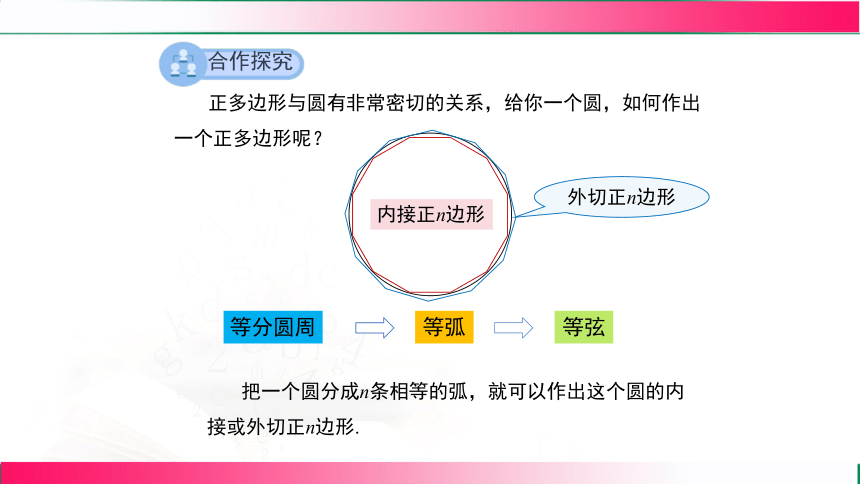
合作探究
正多边形与圆有非常密切的关系,给你一个圆,如何作出一个正多边形呢?
把一个圆分成n条相等的弧,就可以作出这个圆的内接或外切正n边形.
外切正n边形
内接正n边形
等弦
等弧
等分圆周
A
B
C
D
E
O
五边形ABCDE是⊙O的内接正五边形,
五边形PQRST是⊙O的外切正五边形.
合作探究
P
T
Q
R
S
你能证明这个结论吗?
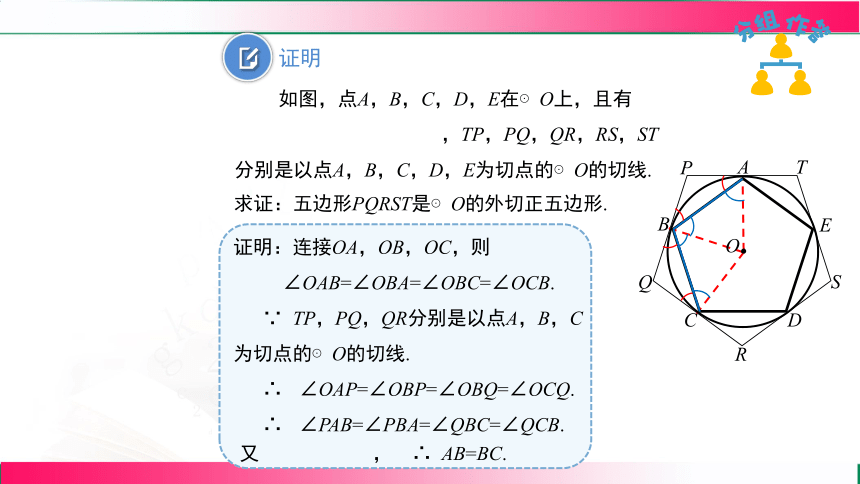
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
于是有:
俩人一组
合作完成
A
B
C
D
E
O
P
T
Q
R
S
同理得
∵ 顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
证明:由 ,得
1
2
3
4
5
证明
求证:五边形ABCDE是⊙O的内接正五边形.
各边相等
各角相等
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
P
T
Q
R
S
证明:连接OA,OB,OC,则
∠OAB=∠OBA=∠OBC=∠OCB.
∵ TP,PQ,QR分别是以点A,B,C为切点的⊙O的切线.
∴ ∠OAP=∠OBP=∠OBQ=∠OCQ.
∴ ∠PAB=∠PBA=∠QBC=∠QCB.
证明
求证:五边形PQRST是⊙O的外切正五边形.
又 , ∴ AB=BC.
A
B
C
D
E
O
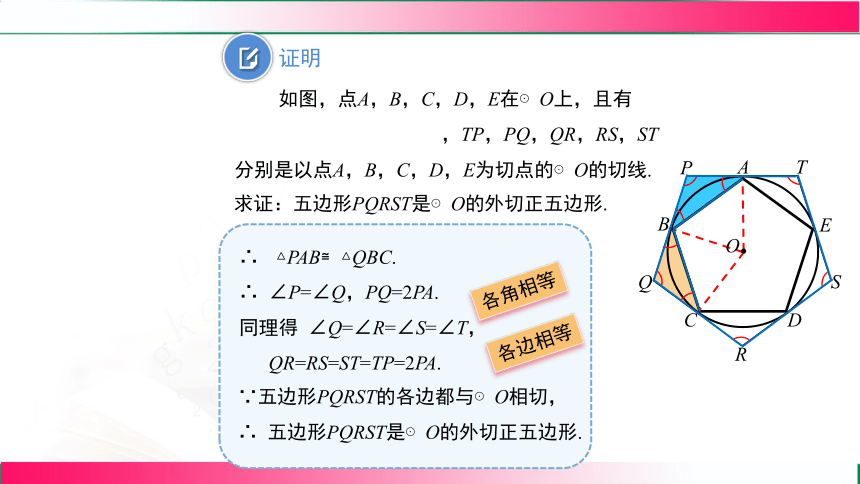
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
∵五边形PQRST的各边都与⊙O相切,
∴ 五边形PQRST是⊙O的外切正五边形.
∴ △PAB≌△QBC.
∴ ∠P=∠Q,PQ=2PA.
同理得 ∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
证明
求证:五边形PQRST是⊙O的外切正五边形.
P
T
Q
R
S
A
B
C
D
E
O
各边相等
各角相等
思考
由上可知,通过等分圆周的方法能作出正n边形.你能说出作正n边形的过程和原理吗?
由在同圆中相等的弦所对的弧相等可知,在同一个圆中,先用量角器作一个等于 的圆心角,这个角所对的弧就是圆周的 ,然后在圆周上依次截取这条弧的等弧,就得到圆的n等份点,从而作出正n边形.
正五角星就是这样作出的
用量角器等分圆周
还有其他的等分圆周的方法吗?
探究
如何在圆中作正四边形?
如图,用直尺和圆规作⊙O 的两条互相垂直的直径(先任意画一条直径,再利用圆规作出直径的垂直平分线),就可以把⊙O分成4等份,顺次连接各分点即可作出正四边形.
用尺规等分圆周
在正四边形的基础上,我们再逐次平分各边所对的弧,就可以作出正八边形、正十六边形等.
归纳
等分圆周的方法
用量角器等分圆周
1
2
用尺规等分圆周
E
F
C
D
A
B
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
正六边形的各边所对的圆心角是多少?
O
2 cm
.
60°
2 cm
△OEF为等边三角形
正六边形的边长等于半径
典型例题
小组合作
1.独立思考,作出图形;
2.两人一组,交流作法.
(1) 任意画一条半径;
(2) 用量角器画一个60°的圆心角,得到它所对的弧;
(3) 用圆规在圆上依次截取与这条弧相等的弧,得到圆的六等份点;
(4) 顺次连接各分点得到正六边形.
用量角器等分圆周
作法:
典型例题
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
还有其他的作法吗?
由于正六边形的边长等于半径,所以在半径为2 cm的圆上依次截取等于2 cm的弦,就可以得到圆的六等份点,顺次连接各分点即可得到圆的内接正六边形.
在正六边形的基础上,逐次等分各边所对的弧,就可作出正十二边形、正二十四边形等.
用尺规等分圆周
连接6等份圆周的相间两个点,可得到正三角形.
典型例题
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
1.给出下列说法:
①各边相等的圆内接多边形是正多边形;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④各角相等的圆外切多边形是正多边形.
其中正确的是( )
A.①④ B.②③ C.①②③④ D.都不正确
返回
【点拨】①各边相等的圆内接多边形是正多边形,正确;②各边相等的圆外切多边形的角不一定相等,如菱形,故②错误;③圆内接矩形,各角相等,但不是正多边形,故③错误;④各角相等的圆外切多边形是正多边形,正确;∴正确的为①④.故选A.
【答案】 A
2.求证:各边相等的圆内接多边形是正多边形.
已知:如图,多边形ABCDE…是⊙O的内接多边形,AB=BC=CD=DE=….求证:多边形ABCDE…是正多边形.
返回
3.下面是“作已知圆的内接正方形”的尺规作图过程.
已知:如图,⊙O.
求作:⊙O的内接正方形.
作法:(1)作⊙O的直径AB;
【解】如图,四边形ACBD即为所作.
证明:由作图知CD为AB的垂直平分线,
∴∠AOC=∠BOC=∠BOD=
∠AOD=90°,且CD经过圆心O,
∴AC=BC=BD=AD,
∴四边形ACBD是菱形.由AB为⊙O的直径,
知∠ACB=90°,∴四边形ACBD是正方形.
返回
4.用尺规作图法作正多边形是数学史上很经典的几何问题,在边数小于10的正多边形中,可以用尺规作图法作出的有正三角形、正四边形、正五边形、正六边形和正八边形,德国数学家高斯已经证明不能用尺规作图法作出正七边形和正九边形,但是我们可以用下面的方法近似地作出一个正七边形:
如图,已知AB为⊙O的直径.
步骤一:作出半径OB的垂直平分线,与⊙O交于E,F两点,垂足为D.
步骤二:以ED为半径,在⊙O上依次
截取BG=GH=HM=MN=NP=PQ=ED.
步骤三:顺次连接各分点,即可得到一个近似的正七边形BGHMNPQ.
请根据上面的方法,用直尺(没有刻度)和圆规在已知⊙O中作出正七边形BGHMNPQ.要求:不写作法,但要保留作图痕迹.
返回
【解】如图所示,七边形BGHMNPQ为所要作的正七边形.
正多边形与圆的关系:
正多边形与圆
等分圆周的方法:
正多边形与圆有非常密切的关系,把一个圆分成n条相等的弧,就可以作出这个圆的内接或外切正n边形.
用量角器等分圆周;
用尺规等分圆周.
1
2
教科书第49页
练习第2、3题
第52页
习题24.6第2题
谢谢观看!
24.6.1正多边形与圆
第24章 圆
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解正多边形与圆的关系;
2.能用尺规作出特殊的正多边形,并设计画出各种相关图案;
(一)导入(5 分钟)
展示生活中各种圆形的物体图片,如车轮、硬币、钟面等。
提问学四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
(七)布置作业(2 分钟)
完成课本上相关的练习题。
测量家里圆形物体的直径或半径,计算其周长和面积,并记录下来。
五、教学反思
在本节课的教学过程中,通过多种教学方法的运用,学生对圆的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实验探究环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的探究能力和实践操作能力。小组合作学习也促进了学生之间的交流与合作。然而,在教学过程中也存在一些不足之处,如在推导圆的面积公式时,部分学生对转化思想的理解还不够深刻;在解决实际问题时,部分学生不能灵活运用所学知识。在今后的教学中,我将进一步加强对学生的引导,注重知识的形成过程,提高学生的数学思维能力和应用能力。
生:“在生活中,你们还见过哪些圆形的物体?这些圆形物体有什么共同特点?” 引导学生观察并思考,从而引出本节课的主题 —— 圆。
(二)圆的认识(10 分钟)
让学生用圆规在纸上画一个圆。
教师在黑板上画圆,并介绍画圆的方法及圆各部分的名称。
圆心:圆中心的一点,用字母 O 表示。圆心确定圆的位置。
半径:连接圆心和圆上任意一点的线段,用字母 r 表示。半径决定圆的大小。
直径:通过圆心并且两端都在圆上的线段,用字母 d 表示。
组织学生分组讨论:在同一个圆里,半径和直径有什么关系?
学生汇报讨论结果,教师总结:在同一个圆里,有无数条半径,无数条直径,所有半径都相等,所有直径都相等,直径的长度是半径的 2 倍,即 d = 2r 或 r = d÷2。
(三)圆的周长(15 分钟)
展示一个圆形物体,提问学生:“什么是圆的周长?” 引导学生理解圆的周长就是围成圆的曲线的长度。
组织学生分组测量圆的周长。提供圆形纸片、直尺、绳子等工具,让学生尝试用不同的方法测量圆的周长。
学生汇报测量方法,教师总结并介绍滚动法和绕线法。
引导学生思考:圆的周长与什么有关?组织学生进行实验探究。测量不同大小圆的直径和周长,并计算周长与直径的比值。
学生汇报实验数据,教师展示表格并引导学生观察发现:圆的周长总是直径的 3 倍多一些。
介绍圆周率的概念:圆的周长与直径的比值是一个固定的数,叫做圆周率,用字母 π 表示。它是一个无限不循环小数,在实际应用中,通常取它的近似值 3.14。
推导出圆的周长计算公式:C = πd 或 C = 2πr。
出示例题,让学生运用公式计算圆的周长。
(四)圆的面积(15 分钟)
提问学生:“什么是圆的面积?” 引导学生理解圆所占平面的大小就是圆的面积。
引导学生思考:如何计算圆的面积?能不能把圆转化成我们学过的图形来计算?
组织学生分组操作:把一个圆形纸片平均分成若干份(如 16 份、32 份等),然后拼成一个近似的长方形。
展示不同份数拼成的近似长方形,让学生观察随着份数的增加,拼成的图形越来越接近长方形。
引导学生分析拼成的长方形与圆的关系:长方形的长相当于圆周长的一半(πr),长方形的宽相当于圆的半径(r)。
根据长方形的面积公式推导出圆的面积公式:S = πr 。
出示例题,让学生运用公式计算圆的面积。
(五)巩固练习(10 分钟)
出示一些关于圆的特征、周长和面积计算的基础练习题,让学生独立完成。
展示一些生活中的实际问题,如计算圆形花坛的周长和面积、圆形桌面的面积等,让学生分组讨论并解决问题。
组织学生进行小组竞赛,出示一些难度稍大的综合性题目,看哪个小组做得又快又准。
(六)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括圆的特征、圆心、半径、直径的概念,圆的周长和面积计算公式等。
强调圆在生活中的广泛应用,鼓励学生在生活中多观察、多思考,运用所学的数学知识解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
什么样的多边形叫做正多边形呢?
复习回顾
各边相等、各角也相等的多边形叫做正多边形.
能否从下图中找出正多边形?
合作探究
正多边形与圆有非常密切的关系,给你一个圆,如何作出一个正多边形呢?
把一个圆分成n条相等的弧,就可以作出这个圆的内接或外切正n边形.
外切正n边形
内接正n边形
等弦
等弧
等分圆周
A
B
C
D
E
O
五边形ABCDE是⊙O的内接正五边形,
五边形PQRST是⊙O的外切正五边形.
合作探究
P
T
Q
R
S
你能证明这个结论吗?
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
于是有:
俩人一组
合作完成
A
B
C
D
E
O
P
T
Q
R
S
同理得
∵ 顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
证明:由 ,得
1
2
3
4
5
证明
求证:五边形ABCDE是⊙O的内接正五边形.
各边相等
各角相等
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
P
T
Q
R
S
证明:连接OA,OB,OC,则
∠OAB=∠OBA=∠OBC=∠OCB.
∵ TP,PQ,QR分别是以点A,B,C为切点的⊙O的切线.
∴ ∠OAP=∠OBP=∠OBQ=∠OCQ.
∴ ∠PAB=∠PBA=∠QBC=∠QCB.
证明
求证:五边形PQRST是⊙O的外切正五边形.
又 , ∴ AB=BC.
A
B
C
D
E
O
如图,点A,B,C,D,E在⊙O上,且有
,TP,PQ,QR,RS,ST分别是以点A,B,C,D,E为切点的⊙O的切线.
∵五边形PQRST的各边都与⊙O相切,
∴ 五边形PQRST是⊙O的外切正五边形.
∴ △PAB≌△QBC.
∴ ∠P=∠Q,PQ=2PA.
同理得 ∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
证明
求证:五边形PQRST是⊙O的外切正五边形.
P
T
Q
R
S
A
B
C
D
E
O
各边相等
各角相等
思考
由上可知,通过等分圆周的方法能作出正n边形.你能说出作正n边形的过程和原理吗?
由在同圆中相等的弦所对的弧相等可知,在同一个圆中,先用量角器作一个等于 的圆心角,这个角所对的弧就是圆周的 ,然后在圆周上依次截取这条弧的等弧,就得到圆的n等份点,从而作出正n边形.
正五角星就是这样作出的
用量角器等分圆周
还有其他的等分圆周的方法吗?
探究
如何在圆中作正四边形?
如图,用直尺和圆规作⊙O 的两条互相垂直的直径(先任意画一条直径,再利用圆规作出直径的垂直平分线),就可以把⊙O分成4等份,顺次连接各分点即可作出正四边形.
用尺规等分圆周
在正四边形的基础上,我们再逐次平分各边所对的弧,就可以作出正八边形、正十六边形等.
归纳
等分圆周的方法
用量角器等分圆周
1
2
用尺规等分圆周
E
F
C
D
A
B
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
正六边形的各边所对的圆心角是多少?
O
2 cm
.
60°
2 cm
△OEF为等边三角形
正六边形的边长等于半径
典型例题
小组合作
1.独立思考,作出图形;
2.两人一组,交流作法.
(1) 任意画一条半径;
(2) 用量角器画一个60°的圆心角,得到它所对的弧;
(3) 用圆规在圆上依次截取与这条弧相等的弧,得到圆的六等份点;
(4) 顺次连接各分点得到正六边形.
用量角器等分圆周
作法:
典型例题
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
还有其他的作法吗?
由于正六边形的边长等于半径,所以在半径为2 cm的圆上依次截取等于2 cm的弦,就可以得到圆的六等份点,顺次连接各分点即可得到圆的内接正六边形.
在正六边形的基础上,逐次等分各边所对的弧,就可作出正十二边形、正二十四边形等.
用尺规等分圆周
连接6等份圆周的相间两个点,可得到正三角形.
典型例题
【例】如图,在一个半径为2 cm的圆中,作出它的内接正六边形.
1.给出下列说法:
①各边相等的圆内接多边形是正多边形;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④各角相等的圆外切多边形是正多边形.
其中正确的是( )
A.①④ B.②③ C.①②③④ D.都不正确
返回
【点拨】①各边相等的圆内接多边形是正多边形,正确;②各边相等的圆外切多边形的角不一定相等,如菱形,故②错误;③圆内接矩形,各角相等,但不是正多边形,故③错误;④各角相等的圆外切多边形是正多边形,正确;∴正确的为①④.故选A.
【答案】 A
2.求证:各边相等的圆内接多边形是正多边形.
已知:如图,多边形ABCDE…是⊙O的内接多边形,AB=BC=CD=DE=….求证:多边形ABCDE…是正多边形.
返回
3.下面是“作已知圆的内接正方形”的尺规作图过程.
已知:如图,⊙O.
求作:⊙O的内接正方形.
作法:(1)作⊙O的直径AB;
【解】如图,四边形ACBD即为所作.
证明:由作图知CD为AB的垂直平分线,
∴∠AOC=∠BOC=∠BOD=
∠AOD=90°,且CD经过圆心O,
∴AC=BC=BD=AD,
∴四边形ACBD是菱形.由AB为⊙O的直径,
知∠ACB=90°,∴四边形ACBD是正方形.
返回
4.用尺规作图法作正多边形是数学史上很经典的几何问题,在边数小于10的正多边形中,可以用尺规作图法作出的有正三角形、正四边形、正五边形、正六边形和正八边形,德国数学家高斯已经证明不能用尺规作图法作出正七边形和正九边形,但是我们可以用下面的方法近似地作出一个正七边形:
如图,已知AB为⊙O的直径.
步骤一:作出半径OB的垂直平分线,与⊙O交于E,F两点,垂足为D.
步骤二:以ED为半径,在⊙O上依次
截取BG=GH=HM=MN=NP=PQ=ED.
步骤三:顺次连接各分点,即可得到一个近似的正七边形BGHMNPQ.
请根据上面的方法,用直尺(没有刻度)和圆规在已知⊙O中作出正七边形BGHMNPQ.要求:不写作法,但要保留作图痕迹.
返回
【解】如图所示,七边形BGHMNPQ为所要作的正七边形.
正多边形与圆的关系:
正多边形与圆
等分圆周的方法:
正多边形与圆有非常密切的关系,把一个圆分成n条相等的弧,就可以作出这个圆的内接或外切正n边形.
用量角器等分圆周;
用尺规等分圆周.
1
2
教科书第49页
练习第2、3题
第52页
习题24.6第2题
谢谢观看!
