25.2.2棱柱与三视图 课件(共28张PPT)
文档属性
| 名称 | 25.2.2棱柱与三视图 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 17:19:19 | ||
图片预览






文档简介
(共28张PPT)
25.2.2棱柱与三视图
第25章 投影与视图
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
能够利用三视图的相关知识解决实际问题;
能够通过简单的三视图还原立体图形本身,并解决面积、体积等问题;
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
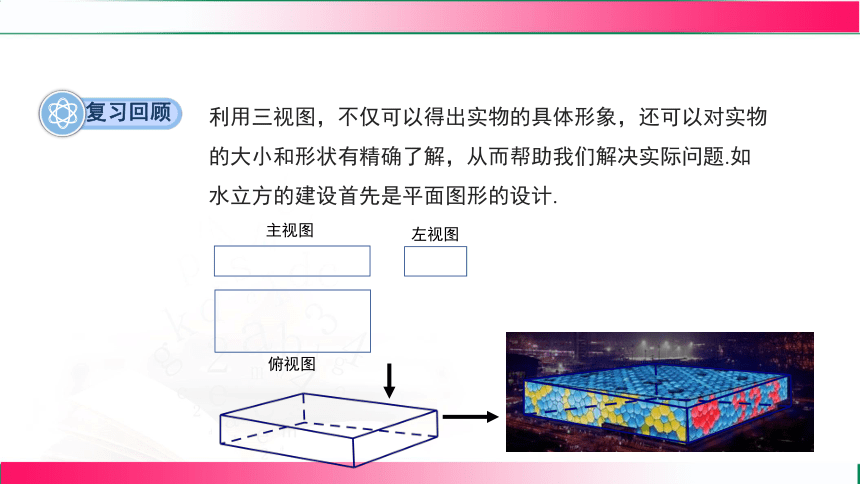
利用三视图,不仅可以得出实物的具体形象,还可以对实物的大小和形状有精确了解,从而帮助我们解决实际问题.如 水立方的建设首先是平面图形的设计.
复习回顾
主视图
俯视图
左视图
探究
现在要做一个模具,它的三视图如下图,你能计算一下它的体积吗?
20cm
32cm
30cm
25cm
40cm
主视图
俯视图
左视图
思路引导:
先根据三视图还原实物,再根据体积公式计算
出体积即可
结论:
上面是一个圆柱,高为32,底面直径是20
下面是一个长方体,高为40,长30,宽25
探究
=(30 000+3 200π) cm3.
体积:
25×30×40+102×32π
≈40048( cm3)
除了体积的计算问题,我们还需要进行表面积的计算问题,
解决方法是一致的,根据三视图还原几何体的长、宽、高等,
根据计算公式进行计算即可.
归纳
由三视图求几何体的表面积或体积的方法:
(1) 先根据给出的三视图确定立体图形
(2)根据三视图的长、宽、高,确定立体图形的长、宽、
高、底面半径等
(3) 最后求出立体图形的表面积或体积.
典型例题
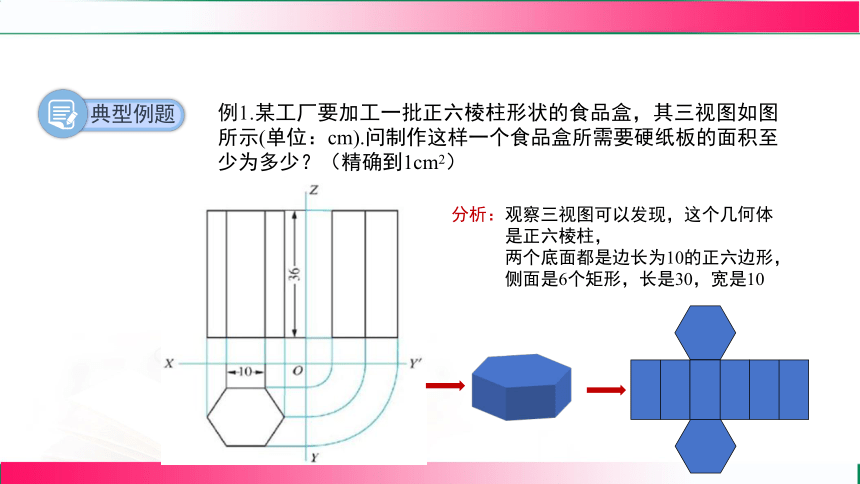
例1.某工厂要加工一批正六棱柱形状的食品盒,其三视图如图所示(单位:cm).问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
分析:观察三视图可以发现,这个几何体
是正六棱柱,
两个底面都是边长为10的正六边形,
侧面是6个矩形,长是30,宽是10
典型例题
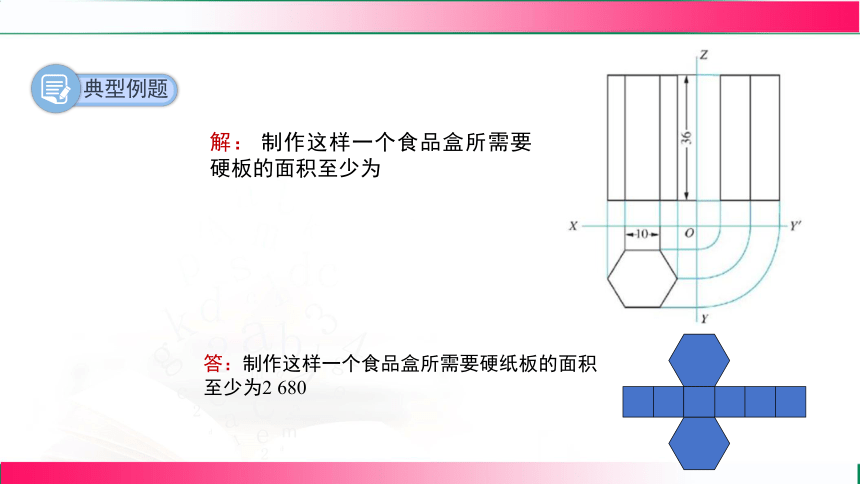
解: 制作这样一个食品盒所需要硬板的面积至少为
答:制作这样一个食品盒所需要硬纸板的面积
至少为2 680
典型例题
例2.一个几何体的三视图如图所示,求这个这个几何体的表面积.
分析:由三视图可知该几何体为
两个长方体的组合体,如图
典型例题
解:主视图的面积=10×60+50×20=1 600,
左视图的面积=40×(50+10)=2 400
俯视图的面积=40×(20+20+20)=2 400,
∴这个几何体的表面积=2×(1 600+2 400+2 400)=12 800.
返回
1.如图,是一个五棱柱,下列关于其叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
D
返回
2. 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”,一个正四棱柱可以平分为两个“堑堵”.一个“堑堵”中,有________个面,________条侧棱.
5
3
返回
3.把如图所示的三棱柱展开,所得到的展开图是( )
B
4. 如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长为多少.
【解】长方体侧面展开图是长方形,长为2×(2+4)=12(cm),宽为5 cm,如图,
由勾股定理得蚂蚁爬行的最短路径PQ长为13 cm.
返回
返回
5.某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图如图所示,这个几何体是( )
A.正方体
B.圆柱
C.圆锥
D.长方体
D
6.如图所示是一个正方体包装盒的表面展开图,在表面展开图上填入适当的数,使得这个表面展开图折成正方体后,相对面上的两数之积相等,则填在A面的数是______.
6
【点拨】∵A面与-1所在的面相对,
-2所在的面与3所在的面相对,
∴填在A面的数是(-2×3)÷(-1)=6.
故答案为6.
返回
7.有四个同学甲、乙、丙、丁画了同一个几何体的展开图如下:
(1)有一个同学画错了,你认为是________;
(2)这个几何体是什么图形?它的体积是多少?
丙
返回
【解】由展开图可知,该几何体是长方体;
它的体积是5×3×2=30(m3).
8.某直三棱柱零件如图①所示,张师傅根据此零件按1∶1的比例画出准确的三视图(如图②).已知在△EFG中,EF=4 cm,∠EFG=45°,FG=12 cm,又知AD=8 cm.求:
(1)AB的长;
(2)这个直三棱柱的体积.
返回
计算简单几合体的表面积和体积
课堂小结
步骤:
计算组合体的表面积与体积
当组合体是由上、下两个四棱柱组成时,表面积就是三个视图的面积和的2倍
三视图在面积体积中的应用
注意:实际问题中计算表面积时,需要确定是否加上底面的面积
(1)由三视图想象出立体图形
(2)确定立体图形的高、底面的长与宽或者直接
(3)根据公式,计算表面积与体积
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
教科书练习
布置作业
谢谢观看!
25.2.2棱柱与三视图
第25章 投影与视图
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
能够利用三视图的相关知识解决实际问题;
能够通过简单的三视图还原立体图形本身,并解决面积、体积等问题;
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
利用三视图,不仅可以得出实物的具体形象,还可以对实物的大小和形状有精确了解,从而帮助我们解决实际问题.如 水立方的建设首先是平面图形的设计.
复习回顾
主视图
俯视图
左视图
探究
现在要做一个模具,它的三视图如下图,你能计算一下它的体积吗?
20cm
32cm
30cm
25cm
40cm
主视图
俯视图
左视图
思路引导:
先根据三视图还原实物,再根据体积公式计算
出体积即可
结论:
上面是一个圆柱,高为32,底面直径是20
下面是一个长方体,高为40,长30,宽25
探究
=(30 000+3 200π) cm3.
体积:
25×30×40+102×32π
≈40048( cm3)
除了体积的计算问题,我们还需要进行表面积的计算问题,
解决方法是一致的,根据三视图还原几何体的长、宽、高等,
根据计算公式进行计算即可.
归纳
由三视图求几何体的表面积或体积的方法:
(1) 先根据给出的三视图确定立体图形
(2)根据三视图的长、宽、高,确定立体图形的长、宽、
高、底面半径等
(3) 最后求出立体图形的表面积或体积.
典型例题
例1.某工厂要加工一批正六棱柱形状的食品盒,其三视图如图所示(单位:cm).问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
分析:观察三视图可以发现,这个几何体
是正六棱柱,
两个底面都是边长为10的正六边形,
侧面是6个矩形,长是30,宽是10
典型例题
解: 制作这样一个食品盒所需要硬板的面积至少为
答:制作这样一个食品盒所需要硬纸板的面积
至少为2 680
典型例题
例2.一个几何体的三视图如图所示,求这个这个几何体的表面积.
分析:由三视图可知该几何体为
两个长方体的组合体,如图
典型例题
解:主视图的面积=10×60+50×20=1 600,
左视图的面积=40×(50+10)=2 400
俯视图的面积=40×(20+20+20)=2 400,
∴这个几何体的表面积=2×(1 600+2 400+2 400)=12 800.
返回
1.如图,是一个五棱柱,下列关于其叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
D
返回
2. 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”,一个正四棱柱可以平分为两个“堑堵”.一个“堑堵”中,有________个面,________条侧棱.
5
3
返回
3.把如图所示的三棱柱展开,所得到的展开图是( )
B
4. 如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长为多少.
【解】长方体侧面展开图是长方形,长为2×(2+4)=12(cm),宽为5 cm,如图,
由勾股定理得蚂蚁爬行的最短路径PQ长为13 cm.
返回
返回
5.某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图如图所示,这个几何体是( )
A.正方体
B.圆柱
C.圆锥
D.长方体
D
6.如图所示是一个正方体包装盒的表面展开图,在表面展开图上填入适当的数,使得这个表面展开图折成正方体后,相对面上的两数之积相等,则填在A面的数是______.
6
【点拨】∵A面与-1所在的面相对,
-2所在的面与3所在的面相对,
∴填在A面的数是(-2×3)÷(-1)=6.
故答案为6.
返回
7.有四个同学甲、乙、丙、丁画了同一个几何体的展开图如下:
(1)有一个同学画错了,你认为是________;
(2)这个几何体是什么图形?它的体积是多少?
丙
返回
【解】由展开图可知,该几何体是长方体;
它的体积是5×3×2=30(m3).
8.某直三棱柱零件如图①所示,张师傅根据此零件按1∶1的比例画出准确的三视图(如图②).已知在△EFG中,EF=4 cm,∠EFG=45°,FG=12 cm,又知AD=8 cm.求:
(1)AB的长;
(2)这个直三棱柱的体积.
返回
计算简单几合体的表面积和体积
课堂小结
步骤:
计算组合体的表面积与体积
当组合体是由上、下两个四棱柱组成时,表面积就是三个视图的面积和的2倍
三视图在面积体积中的应用
注意:实际问题中计算表面积时,需要确定是否加上底面的面积
(1)由三视图想象出立体图形
(2)确定立体图形的高、底面的长与宽或者直接
(3)根据公式,计算表面积与体积
布置作业
教科书习题
探究新知
应用新知
课堂小结
巩固新知
创设情境
教科书练习
布置作业
谢谢观看!
