26.2.2用树状图法求概率 课件(共33张PPT)
文档属性
| 名称 | 26.2.2用树状图法求概率 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 17:21:48 | ||
图片预览








文档简介
(共33张PPT)
26.2.2用树状图法求概率
第26章 概率初步
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握用列表法和画树状图法计算概率.
2.能够根据问题,判断何时选用列表法和画树状图法求概率更方便.
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掷一枚质地均匀的硬币,观察向上的一面.
P(正面向上) ;P(反面向上) .
2.掷两枚质地均匀的硬币,一枚正面向上、一枚反面向上的概率是多少?
正 反
正 (正,正) (正,反)
反 (反,正) (反,反)
第一枚
第二枚
P(一枚正面向上、一枚反面向上) .
思考
如何用列表法解决这个问题?
归纳
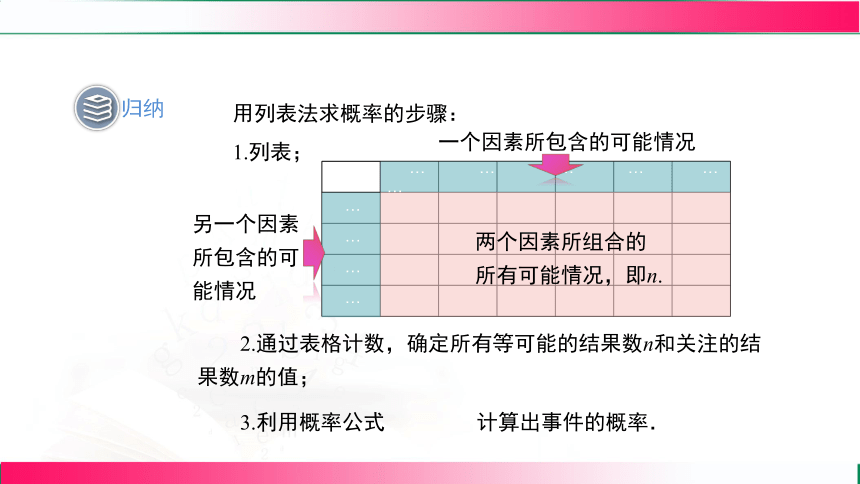
用列表法求概率的步骤:
1.列表;
… … … … … …
一个因素所包含的可能情况
…
…
…
…
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n.
2.通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;
3.利用概率公式 计算出事件的概率.
当一次试验涉及 3 个或更多的因素时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
可以用列表法解决这个问题吗?
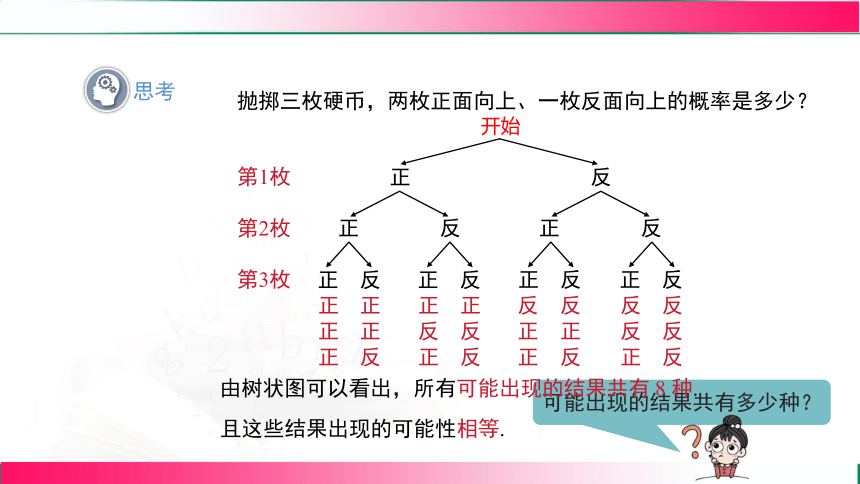
可能出现的结果共有多少种?
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
正
反
第1枚
正
正
正
反正正
正
反正
正
反反
反反正
反正反
正
正
反
反反反
由树状图可以看出,所有可能出现的结果共有 8 种.
且这些结果出现的可能性相等.
开始
第2枚
正
反
正
反
第3枚
正
反
正
反
正
反
正
反
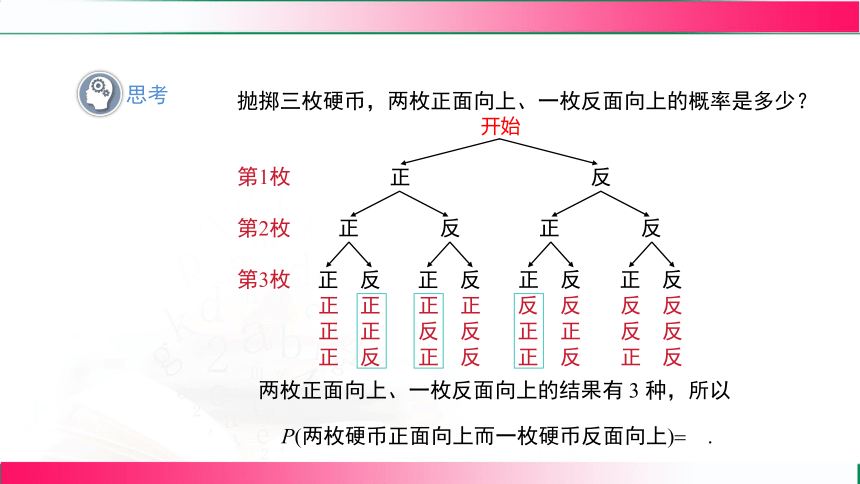
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
正
反
第1枚
正
正
正
反正正
正
反正
正
反反
反反正
反正反
正
正
反
反反反
开始
第2枚
正
反
正
反
第3枚
正
反
正
反
正
反
正
反
两枚正面向上、一枚反面向上的结果有 3 种,所以
P(两枚硬币正面向上而一枚硬币反面向上) .
交流
1. 如何用画树状图法求概率?
2.列表法和树状图法求概率的优点是什么?
3.什么时候使用树状图法方便
1.利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
2.当试验包含两步时,使用列表法或树状图法都可以;当试验在三步或三步以上时,用树状图法更方便.
画树形图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
其中2名都
是女生的结果有4种,
典型例题
例1 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选1人去领奖,求2人都是女生的概率.
解:设2名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.
开始
获演唱奖的
获演奏奖的
男
女''
女'
女1
男2
男1
女2
女1
男2
男1
女2
女1
男2
男1
女2
共有12种结果,
且每种结果出现的可能性相等,
所以事件A发生的概率为P(A) .
计算等可能情形下概念的关键是确定所有可能性相等的结果总数n和求出事件A发生的结果总数m,“树状图”能帮助我们有序的思考,不重复,不遗漏地得出n和m.
典型例题
例2 甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C,D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.
(1)取出的 3 个小球上恰好有 1 个、2 个和 3 个元音字母的概率分别是多少?
(2)取出的 3 个小球上全是辅音字母的概率是多少?
A
B
E
D
C
H
I
典型例题
A
B
E
D
C
H
I
解:根据题意,可以画出如下树状图:
开始
甲
A
B
C
E
D
乙
C
E
D
丙
H
I
H
I
H
I
H
I
H
I
H
I
典型例题
由树状图可以看出,可能出现的结果共有 12 种,且这些结果出现的可能性相等.
(1)取出的 3 个小球上恰好有 1 个元音字母的结果有 5 种,即ACH、ADH、BCI、BDI、BEH,所以
恰有 2 个元音字母的结果有 4 种,即ACI、ADI、AEH、BEI,所以
恰有3个元音字母的结果有1种,即AEI,所以
P(1个元音) .
P(2个元音) .
P(3个元音) .
典型例题
由树状图可以看出,可能出现的结果共有 12 种,且这些结果出现的可能性相等.
(2)取出的 3 个小球上全是辅音字母的结果有2 种,即BCH、BDH,所以
P(3个辅音) .
1.[2024·重庆] 重庆是一座魔幻都市,有着丰富的旅游资源.甲、乙两人相约来到重庆旅游,两人分别从A,B,C三个景点中随机选择一个景点游览,甲、乙两人同时选择景点B的概率为________.
返回
返回
【答案】 B
返回
【答案】 D
返回
【答案】 B
5.吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道靓丽的风景线,某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.
若三个项目被抽中的可能性相等,用画树状图的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
【解】将抽中“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为事件A,B,C,可画树状图为:
返回
返回
C
【点拨】氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,分别用A,B,C,D表示,
画树状图如图:
列表法求概率的步骤
1.列表;
2.通过表格,确定所有等可能的结果数n和关注的结果数m的值;
3.利用概率公式 计算出事件的概率.
列表法
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
课堂小结
用列表法求概率
树状图法:
当一次试验涉及 3 个或更多的因素时,为不重不漏地列出所有可能的结果,通常采用画树状图法.
画树形图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
课堂小结
画树状图法求概率
教科书练习
布置作业
谢谢观看!
26.2.2用树状图法求概率
第26章 概率初步
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握用列表法和画树状图法计算概率.
2.能够根据问题,判断何时选用列表法和画树状图法求概率更方便.
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掷一枚质地均匀的硬币,观察向上的一面.
P(正面向上) ;P(反面向上) .
2.掷两枚质地均匀的硬币,一枚正面向上、一枚反面向上的概率是多少?
正 反
正 (正,正) (正,反)
反 (反,正) (反,反)
第一枚
第二枚
P(一枚正面向上、一枚反面向上) .
思考
如何用列表法解决这个问题?
归纳
用列表法求概率的步骤:
1.列表;
… … … … … …
一个因素所包含的可能情况
…
…
…
…
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n.
2.通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;
3.利用概率公式 计算出事件的概率.
当一次试验涉及 3 个或更多的因素时,列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法.
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
可以用列表法解决这个问题吗?
可能出现的结果共有多少种?
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
正
反
第1枚
正
正
正
反正正
正
反正
正
反反
反反正
反正反
正
正
反
反反反
由树状图可以看出,所有可能出现的结果共有 8 种.
且这些结果出现的可能性相等.
开始
第2枚
正
反
正
反
第3枚
正
反
正
反
正
反
正
反
抛掷三枚硬币,两枚正面向上、一枚反面向上的概率是多少?
思考
正
反
第1枚
正
正
正
反正正
正
反正
正
反反
反反正
反正反
正
正
反
反反反
开始
第2枚
正
反
正
反
第3枚
正
反
正
反
正
反
正
反
两枚正面向上、一枚反面向上的结果有 3 种,所以
P(两枚硬币正面向上而一枚硬币反面向上) .
交流
1. 如何用画树状图法求概率?
2.列表法和树状图法求概率的优点是什么?
3.什么时候使用树状图法方便
1.利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
2.当试验包含两步时,使用列表法或树状图法都可以;当试验在三步或三步以上时,用树状图法更方便.
画树形图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
其中2名都
是女生的结果有4种,
典型例题
例1 某班有1名男生,2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选1人去领奖,求2人都是女生的概率.
解:设2名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.
开始
获演唱奖的
获演奏奖的
男
女''
女'
女1
男2
男1
女2
女1
男2
男1
女2
女1
男2
男1
女2
共有12种结果,
且每种结果出现的可能性相等,
所以事件A发生的概率为P(A) .
计算等可能情形下概念的关键是确定所有可能性相等的结果总数n和求出事件A发生的结果总数m,“树状图”能帮助我们有序的思考,不重复,不遗漏地得出n和m.
典型例题
例2 甲、乙、丙三个盒中分别装有大小、形状、质地相同的小球若干,甲盒中装有2个小球,分别写有字母A和B;乙盒中装有3个小球,分别写有字母C,D和E;丙盒中装有2个小球,分别写有字母H和I;现要从3个盒中各随机取出1个小球.
(1)取出的 3 个小球上恰好有 1 个、2 个和 3 个元音字母的概率分别是多少?
(2)取出的 3 个小球上全是辅音字母的概率是多少?
A
B
E
D
C
H
I
典型例题
A
B
E
D
C
H
I
解:根据题意,可以画出如下树状图:
开始
甲
A
B
C
E
D
乙
C
E
D
丙
H
I
H
I
H
I
H
I
H
I
H
I
典型例题
由树状图可以看出,可能出现的结果共有 12 种,且这些结果出现的可能性相等.
(1)取出的 3 个小球上恰好有 1 个元音字母的结果有 5 种,即ACH、ADH、BCI、BDI、BEH,所以
恰有 2 个元音字母的结果有 4 种,即ACI、ADI、AEH、BEI,所以
恰有3个元音字母的结果有1种,即AEI,所以
P(1个元音) .
P(2个元音) .
P(3个元音) .
典型例题
由树状图可以看出,可能出现的结果共有 12 种,且这些结果出现的可能性相等.
(2)取出的 3 个小球上全是辅音字母的结果有2 种,即BCH、BDH,所以
P(3个辅音) .
1.[2024·重庆] 重庆是一座魔幻都市,有着丰富的旅游资源.甲、乙两人相约来到重庆旅游,两人分别从A,B,C三个景点中随机选择一个景点游览,甲、乙两人同时选择景点B的概率为________.
返回
返回
【答案】 B
返回
【答案】 D
返回
【答案】 B
5.吉林省以“绿水青山就是金山银山,冰天雪地也是金山银山”为指引,不断加大冰雪旅游的宣传力度,推出各种优惠活动,“小土豆”“小砂糖橘”等成为一道靓丽的风景线,某滑雪场为吸引游客,每天抽取一定数量的幸运游客,每名幸运游客可以从“滑雪”“滑雪圈”“雪地摩托”三个项目中随机抽取一个免费游玩.
若三个项目被抽中的可能性相等,用画树状图的方法,求幸运游客小明与小亮恰好抽中同一个项目的概率.
【解】将抽中“滑雪”“滑雪圈”“雪地摩托”三个项目分别记为事件A,B,C,可画树状图为:
返回
返回
C
【点拨】氢氧化钠溶液,碳酸氢钠溶液,稀盐酸溶液和稀硫酸溶液,分别用A,B,C,D表示,
画树状图如图:
列表法求概率的步骤
1.列表;
2.通过表格,确定所有等可能的结果数n和关注的结果数m的值;
3.利用概率公式 计算出事件的概率.
列表法
当一个试验有两个相关因素,且所有可能的结果较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
课堂小结
用列表法求概率
树状图法:
当一次试验涉及 3 个或更多的因素时,为不重不漏地列出所有可能的结果,通常采用画树状图法.
画树形图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件A包含的结果数m,试验的所有可能结果数n;
(4)用概率公式进行计算.
课堂小结
画树状图法求概率
教科书练习
布置作业
谢谢观看!
