26.3用频率估计概率 课件(共39张PPT)
文档属性
| 名称 | 26.3用频率估计概率 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 17:23:01 | ||
图片预览






文档简介
(共39张PPT)
26.3用频率估计概率
第26章 概率初步
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.通过实验与操作,体会随机事件在每一次实验中发生与否具有不确定性,理解重复实验的次数与事件发生的频率之间的关系;
2.了解频率和概率的区别与联系,能从频率值角度估计随机事件发生的概率;
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
P(正面向上) P(反面向上) .
问题引入
抛掷一枚质地均匀的硬币,
(1)硬币落地后,观察向上一面,会出现哪些可能的结果?
正面向上
反面向上
(2)“正面向上”和“反面向上”的概率分别是多少?
抛掷一枚硬币50次,一定会有25次出现正面和25次出现反面吗?
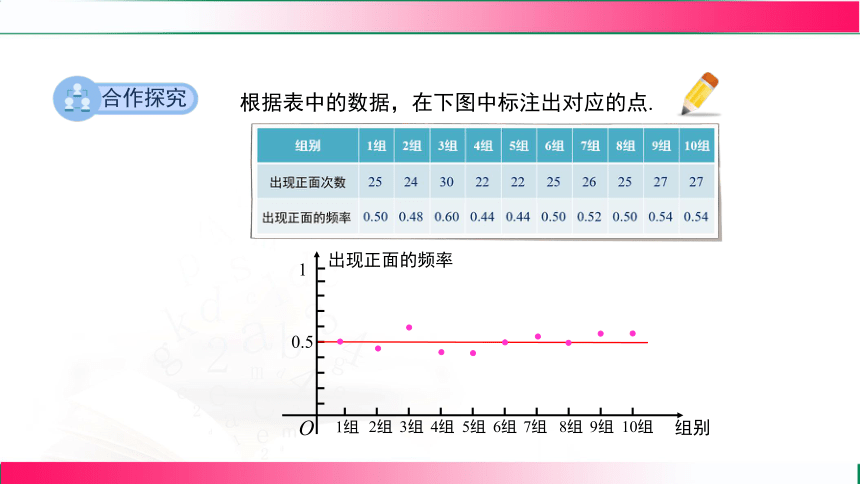
组别 1组 2组 3组 4组 5组 6组 7组 8组 9组 10组
出现正面次数
出现正面的频率
请同学们分组进行抛掷硬币试验,每组抛掷一枚硬币50次,统计出现正面的次数,计算频率,并完成下面的表格.
结果保留小数点后两位
小组合作
1.三人一组抛掷硬币;
2.第1名同学负责抛掷硬币,报告试验结果,
第2名同学记录试验结果,第3名同学监督.
合作探究
组别 1组 2组 3组 4组 5组 6组 7组 8组 9组 10组
出现正面次数
出现正面的频率
请同学们分组进行抛掷硬币试验,每组抛掷一枚硬币50次,统计出现正面的次数,计算频率,并完成下面的表格.
25
24
30
22
22
25
26
25
27
27
0.50
0.48
0.60
0.44
0.44
0.50
0.52
0.50
0.54
0.54
合作探究
根据表中的数据,在下图中标注出对应的点.
组别
O
1组
0.5
2组
3组
4组
5组
6组
7组
8组
9组
10组
出现正面的频率
1
合作探究
合作探究
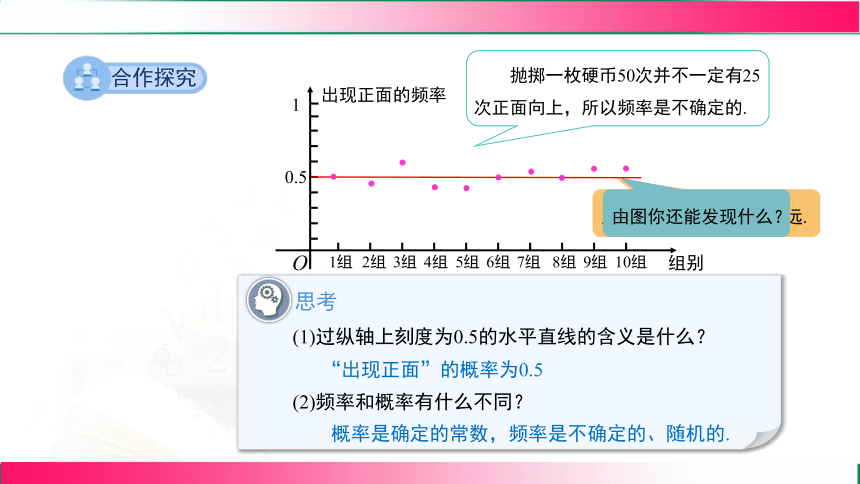
思考
(1)过纵轴上刻度为0.5的水平直线的含义是什么?
(2)频率和概率有什么不同?
“出现正面”的概率为0.5
概率是确定的常数,频率是不确定的、随机的.
大部分组的频率离0.5不远.
由图你还能发现什么?
组别
O
1组
0.5
2组
3组
4组
5组
6组
7组
8组
9组
10组
出现正面的频率
1
抛掷一枚硬币50次并不一定有25次正面向上,所以频率是不确定的.
一位同学在做“抛硬币”的试验中,将获得的数据绘制成下表及折线统计图:
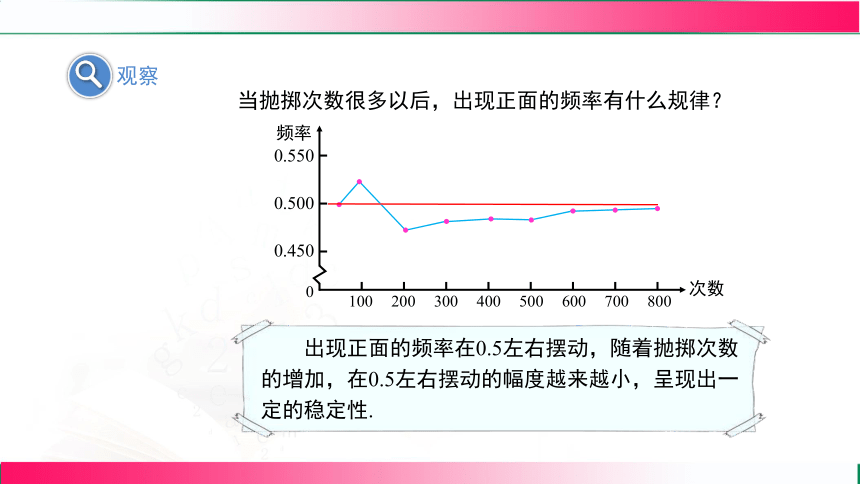
抛掷次数 50 100 200 300 400 500 600 700 800
出现正面次数 25 52 95 145 195 243 295 345 396
出现正面的频率 0.500 0.520 0.475 0.483 0.488 0.486 0.492 0.493 0.495
次数
0
0.450
200
300
400
500
600
700
800
频率
0.550
100
0.500
思考
如果增加试验次数,频率会如何变化?
当抛掷次数很多以后,出现正面的频率有什么规律?
次数
0
0.450
200
300
400
500
600
700
800
频率
0.550
100
0.500
出现正面的频率在0.5左右摆动,随着抛掷次数的增加,在0.5左右摆动的幅度越来越小,呈现出一定的稳定性.
观察
观察
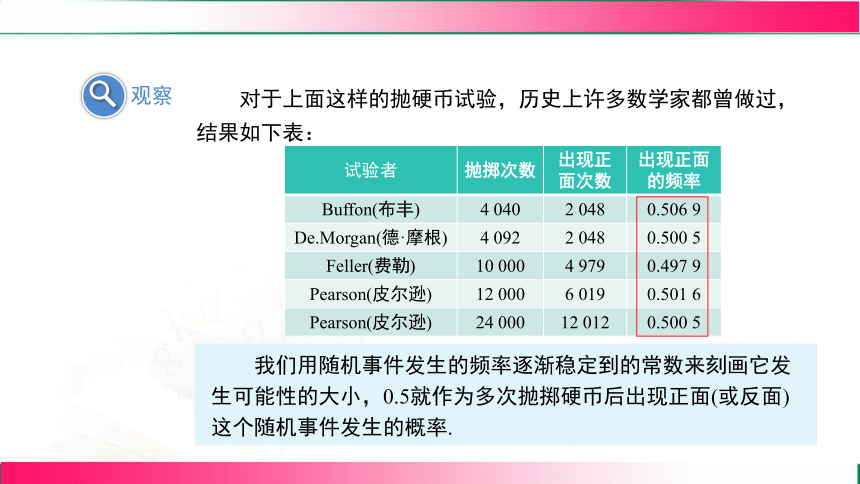
对于上面这样的抛硬币试验,历史上许多数学家都曾做过,结果如下表:
试验者 抛掷次数 出现正面次数 出现正面的频率
Buffon(布丰) 4 040 2 048 0.506 9
De.Morgan(德·摩根) 4 092 2 048 0.500 5
Feller(费勒) 10 000 4 979 0.497 9
Pearson(皮尔逊) 12 000 6 019 0.501 6
Pearson(皮尔逊) 24 000 12 012 0.500 5
由表观察出现正面的频率的变化趋势是什么?
出现正面的频率逐渐稳定到常数0.5.
我们用随机事件发生的频率逐渐稳定到的常数来刻画它发生可能性的大小,0.5就作为多次抛掷硬币后出现正面(或反面)这个随机事件发生的概率.
观察
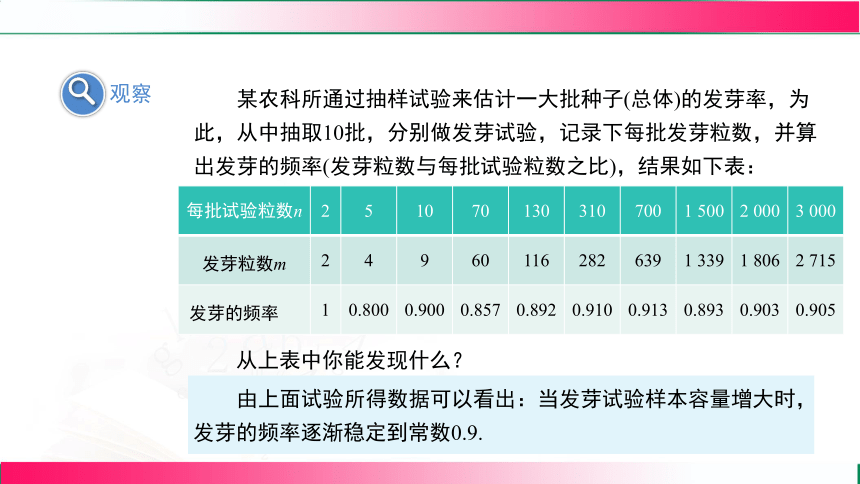
某农科所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验,记录下每批发芽粒数,并算出发芽的频率(发芽粒数与每批试验粒数之比),结果如下表:
每批试验粒数n 2 5 10 70 130 310 700 1 500 2 000 3 000
发芽粒数m 2 4 9 60 116 282 639 1 339 1 806 2 715
发芽的频率 1 0.800 0.900 0.857 0.892 0.910 0.913 0.893 0.903 0.905
从上表中你能发现什么?
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
观察
某乒兵球生产厂,从最近生产的一大批乒兵球中,抽取6批进行质量检测,结果如下表:
每批抽取球数n 50 100 200 500 1 000 2 000
优等品数m 45 92 1949 470 954 1 902
优等品的频率 0.900 0.920 0.970 0.940 0.954 0.951
从上表中你能发现什么?
由上面检测所得数据可以看出:当质量检测样本容量增大时,优等品的频率逐渐稳定到常数0.95.
归纳
一般地,在大量重复试验下,随机事件A发生的频率
(这里n是总试验次数,它必须相当大,m是在n次试验中随机事件A发生的次数)
会稳定到某个常数p.
于是,我们用p这个常数表示随机事件A发生的概率,
即:P(A) p.
我们可以通过大量重复试验,用一个随机事件发生的 去估计它的 .
频率
概率
频率 概率
区别
联系
归纳
频率与概率的区别与联系
不确定的数
(试验值或使用的统计值)
确定的常数
(理论值)
与试验次数的变化有关
与试验次数的变化无关
与试验人、试验时间、
试验地点有关
与试验人、试验时间、
试验地点无关
试验次数越多,频率越趋向于概率
典型例题
例1 某射手在同一条件下进行多次射击,结果如下表:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)计算表中“击中靶心的频率”;
(2)这个射手射击1次,击中靶心的概率约是多少?
解:(1)如上表;
(2)从上表数据可以看出,随着射击次数的增多,击中靶心的频率稳定在常数0.9附近,
故这个射手射击1次,击中靶心的概率约是0.9.
0.80
0.95
0.88
0.92
0.89
0.91
1.关于频率和概率的关系,下列说法正确的是( )
A.当试验次数很大时,概率稳定在频率附近
B.试验得到的频率与概率不可能相等
C.当试验次数很大时,频率稳定在概率附近
D.频率等于概率
【点拨】A.概率是定值,故本选项错误,不符合题意;
B.试验得到的频率与概率可能相等,故本选项错误,不符合题意;C.当试验次数很大时,频率稳定在概率附近,正确,故本选项符合题意;D.频率只能估计概率,故本选项错误,不符合题意.故选C.
返回
【答案】 C
2.[2024·贵州] 小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.4,下列说法正确的是( )
A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次
D.小星定点投篮4次,一定投中1次
A
返回
3.[2024·扬州]数学兴趣小组做抛掷一枚瓶盖的实验后,整理的实
验数据如
下表:
累计抛掷次数 盖面朝上次数 盖面朝上频率
50 28 0.560 0
100 54 0.540 0
200 106 0.530 0
300 158 0.526 7
500 264 0.528 0
1 000 527 0.527 0
2 000 1 056 0.528 0
3 000 1 587 0.529 0
5 000 2 650 0.530 0
返回
根据以上实验数据可以估计出“盖面朝上”的概率约为________(精确到0.01).
0.53
4.[2024·滁州模拟]某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,
则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任意抽一张牌的花色是黑桃
C.一只不透明袋子中有1个红球和3个绿球(除了颜色都相同),从中任意摸出一个球是红球
D.掷一枚质地均匀的正方体骰子,向上一面的点数是5
返回
【答案】 D
5.[2024·宿迁期中]小乐同学将新华书店的阅读二维码打印在面积为400cm2的正方形纸上,如图所示,为了估计图中黑色部分的面积,他在纸内随机掷点,经过大量重复试验,发现点落入黑色部分的频
率稳定在0.4左右,据此可以估计黑色
部分的面积约为________cm2.
160
返回
【点拨】400×0.4=160(cm2),即黑色部分的面积约为160cm2.
6.《数书九章》是我国南宋数学家秦九韶所著的数学著作,标志着中国古代数学的高峰.书中记载有这样一道题目:粮仓开仓收粮,有人送来米2 000石,验得米内夹谷,抽样取米一把,数得300粒米内夹谷36粒,则这批米内夹谷约为________石.
240
返回
7.某区七年级有3 000名学生参加“安全伴我行知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分(得分取正整数,满分为100分)进行统计.
分组(分) 频数 频率
49.5~59.5 10
59.5~69.5 16 0.08
69.5~79.5 0.20
79.5~89.5 62
89.5~100.5 72 0.36
请你根据不完整的频率分布表,解答下列问题:
(1)补全如图所示的频数直方图;
【解】补全频数直方图如图所示.
(2)若将得分转化为等级,规定得分低于59.5分评为“D”, 59.5~69.5分评为“C”, 69.5~89.5分评为“B”, 89.5~100.5分评为“A”.这次全区七年级参加竞赛的学生中约有多少名学生参赛成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩被评为“A”“B”“C”“D”哪一个等级的可能性大?请说明理由.
返回
∴P(B)>P(A)>P(C)>P(D),
∴随机抽查一名参赛学生的成绩等级,这名学生的成绩被评为“B”的可能性大.
用频率估计概率
我们可以通过大量重复试验,用一个随机事件发生的频率去估计它的概率.
频率与概率的区别与联系:
概率是确定的常数,频率是不确定的、随机的,受试验条件影响.试验次数越多,频率越趋向于概率.
课堂小结
用频率估计概率
教科书练习
布置作业
谢谢观看!
26.3用频率估计概率
第26章 概率初步
沪科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.通过实验与操作,体会随机事件在每一次实验中发生与否具有不确定性,理解重复实验的次数与事件发生的频率之间的关系;
2.了解频率和概率的区别与联系,能从频率值角度估计随机事件发生的概率;
展示物体在平行光线下不同角度的投影图片,引出正投影的概念:在平行投影中,如果投影线垂直于投影面,那么这种投影称为正投影。
实验探究:准备一些简单的几何体(如正方体、长方体、圆柱等),让学生用手电筒(模拟平行光线)垂直照射这些几何体,观察并记录它们在水平投影面上的正投影形状和大小。
组织学生分组讨论,总结正投影的性质:
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同。
当物体的某个面倾斜于投影面时,这个面的正投影变小。
当物体的某个面垂直于投影面时,这个面的正投影成为一条线段。
通过具体的例题,让学生运用正投影的性质判断物体不同位置的正投影形状和大小,加深学生对正投影性质的理解。
(四)视图的概念与三视图的画法(15 分钟)
展示一个简单几何体(如正方体)从不同方向看的图片,讲解视图的概念:当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
介绍三视图的概念:
主视图:从正面看到的图形,称为主视图。
俯视图:从上面看到的图形,称为俯视图。
左视图:从左面看到的图形,称为左视图。
以正方体为例,教师在黑板上示范画三视图的步骤:
先画主视图,确定正方体的长和高。
再画俯视图,注意俯视图要与主视图长对正,确定正方体的长和宽。
最后画左视图,左视图要与主视图高平齐,与俯视图宽相等。
让学生自己动手画正方体的三视图,教师巡视指导,及时纠正学生画图过程中出现的问题,如视图的位置、线条的虚实等。
给出一些其他简单几何体(如圆柱、圆锥、三棱柱等),让学生分组画出它们的三视图,然后小组之间互相交流、评价。
(五)由三视图描述几何体(10 分钟)
展示一些简单几何体的三视图,让学生观察并思考每个三视图所对应的几何体形状。
组织学生分组讨论,根据三视图的特征(如视图的形状、大小、位置关系等)来推断几何体的形状。
小组汇报讨论结果,教师引导学生总结由三视图描述几何体形状的方法:
先根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状,然后综合起来考虑整体形状。
注意视图中的线条和形状所代表的实际意义,如视图中的矩形可能表示长方体的面,圆形可能表示圆柱的底面等。
通过一些具体的练习题,让学生进一步巩固由三视图描述几何体形状的能力。
(六)巩固练习(10 分钟)
出示一些关于投影概念、性质判断的基础练习题,如选择题、填空题,让学生独立完成,巩固对基础知识的掌握。
展示一些简单几何体的实物或图片,要求学生画出它们的三视图,然后同桌之间互相检查批改。
给出一些几何体的三视图,让学生说出对应的几何体名称,并描述其特征,培养学生的空间想象能力和语言表达能力。
展示一些生活中的实际问题,如根据建筑物的设计图纸(三视图)想象建筑物的实际形状、根据零件的三视图计算零件的体积等,让学生分组讨论并解决问题,提高学生运用所学知识解决实际问题的能力。
(七)课堂总结(3 分钟)
与学生一起回顾本节课所学的主要内容,包括投影的概念、分类(平行投影、中心投影)、正投影的性质,以及视图的概念、三视图的画法和由三视图描述几何体的方法。
强调投影与视图在生活中的广泛应用,鼓励学生在日常生活中多观察、多思考,运用所学的数学知识去理解和解决实际问题。
(八)布置作业(2 分钟)
完成课本上相关的练习题,进一步巩固所学知识。
观察生活中的物体,选择一些简单的几何体,画出它们的三视图,并标注出各部分的尺寸。
五、教学反思
在本节课的教学过程中,通过多种教学方法的综合运用,学生对投影与视图的知识有了较为深入的理解和掌握,达到了预期的教学目标。在实践探究和小组合作环节,学生积极参与,亲身体验了知识的形成过程,培养了学生的实践操作能力和合作交流能力。然而,在教学过程中也存在一些不足之处,例如在讲解由三视图描述几何体形状时,部分学生的空间想象能力还有待提高,对一些复杂的三视图理解起来较为困难;在让学生画三视图时,仍有少数学生不能准确把握视图之间的位置关系和尺寸比例。在今后的教学中,我将进一步加强对这些难点内容的教学,增加更多的实例和练习,帮助学生更好地建立空间观念,提高学生的空间想象能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
P(正面向上) P(反面向上) .
问题引入
抛掷一枚质地均匀的硬币,
(1)硬币落地后,观察向上一面,会出现哪些可能的结果?
正面向上
反面向上
(2)“正面向上”和“反面向上”的概率分别是多少?
抛掷一枚硬币50次,一定会有25次出现正面和25次出现反面吗?
组别 1组 2组 3组 4组 5组 6组 7组 8组 9组 10组
出现正面次数
出现正面的频率
请同学们分组进行抛掷硬币试验,每组抛掷一枚硬币50次,统计出现正面的次数,计算频率,并完成下面的表格.
结果保留小数点后两位
小组合作
1.三人一组抛掷硬币;
2.第1名同学负责抛掷硬币,报告试验结果,
第2名同学记录试验结果,第3名同学监督.
合作探究
组别 1组 2组 3组 4组 5组 6组 7组 8组 9组 10组
出现正面次数
出现正面的频率
请同学们分组进行抛掷硬币试验,每组抛掷一枚硬币50次,统计出现正面的次数,计算频率,并完成下面的表格.
25
24
30
22
22
25
26
25
27
27
0.50
0.48
0.60
0.44
0.44
0.50
0.52
0.50
0.54
0.54
合作探究
根据表中的数据,在下图中标注出对应的点.
组别
O
1组
0.5
2组
3组
4组
5组
6组
7组
8组
9组
10组
出现正面的频率
1
合作探究
合作探究
思考
(1)过纵轴上刻度为0.5的水平直线的含义是什么?
(2)频率和概率有什么不同?
“出现正面”的概率为0.5
概率是确定的常数,频率是不确定的、随机的.
大部分组的频率离0.5不远.
由图你还能发现什么?
组别
O
1组
0.5
2组
3组
4组
5组
6组
7组
8组
9组
10组
出现正面的频率
1
抛掷一枚硬币50次并不一定有25次正面向上,所以频率是不确定的.
一位同学在做“抛硬币”的试验中,将获得的数据绘制成下表及折线统计图:
抛掷次数 50 100 200 300 400 500 600 700 800
出现正面次数 25 52 95 145 195 243 295 345 396
出现正面的频率 0.500 0.520 0.475 0.483 0.488 0.486 0.492 0.493 0.495
次数
0
0.450
200
300
400
500
600
700
800
频率
0.550
100
0.500
思考
如果增加试验次数,频率会如何变化?
当抛掷次数很多以后,出现正面的频率有什么规律?
次数
0
0.450
200
300
400
500
600
700
800
频率
0.550
100
0.500
出现正面的频率在0.5左右摆动,随着抛掷次数的增加,在0.5左右摆动的幅度越来越小,呈现出一定的稳定性.
观察
观察
对于上面这样的抛硬币试验,历史上许多数学家都曾做过,结果如下表:
试验者 抛掷次数 出现正面次数 出现正面的频率
Buffon(布丰) 4 040 2 048 0.506 9
De.Morgan(德·摩根) 4 092 2 048 0.500 5
Feller(费勒) 10 000 4 979 0.497 9
Pearson(皮尔逊) 12 000 6 019 0.501 6
Pearson(皮尔逊) 24 000 12 012 0.500 5
由表观察出现正面的频率的变化趋势是什么?
出现正面的频率逐渐稳定到常数0.5.
我们用随机事件发生的频率逐渐稳定到的常数来刻画它发生可能性的大小,0.5就作为多次抛掷硬币后出现正面(或反面)这个随机事件发生的概率.
观察
某农科所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验,记录下每批发芽粒数,并算出发芽的频率(发芽粒数与每批试验粒数之比),结果如下表:
每批试验粒数n 2 5 10 70 130 310 700 1 500 2 000 3 000
发芽粒数m 2 4 9 60 116 282 639 1 339 1 806 2 715
发芽的频率 1 0.800 0.900 0.857 0.892 0.910 0.913 0.893 0.903 0.905
从上表中你能发现什么?
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
观察
某乒兵球生产厂,从最近生产的一大批乒兵球中,抽取6批进行质量检测,结果如下表:
每批抽取球数n 50 100 200 500 1 000 2 000
优等品数m 45 92 1949 470 954 1 902
优等品的频率 0.900 0.920 0.970 0.940 0.954 0.951
从上表中你能发现什么?
由上面检测所得数据可以看出:当质量检测样本容量增大时,优等品的频率逐渐稳定到常数0.95.
归纳
一般地,在大量重复试验下,随机事件A发生的频率
(这里n是总试验次数,它必须相当大,m是在n次试验中随机事件A发生的次数)
会稳定到某个常数p.
于是,我们用p这个常数表示随机事件A发生的概率,
即:P(A) p.
我们可以通过大量重复试验,用一个随机事件发生的 去估计它的 .
频率
概率
频率 概率
区别
联系
归纳
频率与概率的区别与联系
不确定的数
(试验值或使用的统计值)
确定的常数
(理论值)
与试验次数的变化有关
与试验次数的变化无关
与试验人、试验时间、
试验地点有关
与试验人、试验时间、
试验地点无关
试验次数越多,频率越趋向于概率
典型例题
例1 某射手在同一条件下进行多次射击,结果如下表:
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
(1)计算表中“击中靶心的频率”;
(2)这个射手射击1次,击中靶心的概率约是多少?
解:(1)如上表;
(2)从上表数据可以看出,随着射击次数的增多,击中靶心的频率稳定在常数0.9附近,
故这个射手射击1次,击中靶心的概率约是0.9.
0.80
0.95
0.88
0.92
0.89
0.91
1.关于频率和概率的关系,下列说法正确的是( )
A.当试验次数很大时,概率稳定在频率附近
B.试验得到的频率与概率不可能相等
C.当试验次数很大时,频率稳定在概率附近
D.频率等于概率
【点拨】A.概率是定值,故本选项错误,不符合题意;
B.试验得到的频率与概率可能相等,故本选项错误,不符合题意;C.当试验次数很大时,频率稳定在概率附近,正确,故本选项符合题意;D.频率只能估计概率,故本选项错误,不符合题意.故选C.
返回
【答案】 C
2.[2024·贵州] 小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.4,下列说法正确的是( )
A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次
D.小星定点投篮4次,一定投中1次
A
返回
3.[2024·扬州]数学兴趣小组做抛掷一枚瓶盖的实验后,整理的实
验数据如
下表:
累计抛掷次数 盖面朝上次数 盖面朝上频率
50 28 0.560 0
100 54 0.540 0
200 106 0.530 0
300 158 0.526 7
500 264 0.528 0
1 000 527 0.527 0
2 000 1 056 0.528 0
3 000 1 587 0.529 0
5 000 2 650 0.530 0
返回
根据以上实验数据可以估计出“盖面朝上”的概率约为________(精确到0.01).
0.53
4.[2024·滁州模拟]某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,
则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任意抽一张牌的花色是黑桃
C.一只不透明袋子中有1个红球和3个绿球(除了颜色都相同),从中任意摸出一个球是红球
D.掷一枚质地均匀的正方体骰子,向上一面的点数是5
返回
【答案】 D
5.[2024·宿迁期中]小乐同学将新华书店的阅读二维码打印在面积为400cm2的正方形纸上,如图所示,为了估计图中黑色部分的面积,他在纸内随机掷点,经过大量重复试验,发现点落入黑色部分的频
率稳定在0.4左右,据此可以估计黑色
部分的面积约为________cm2.
160
返回
【点拨】400×0.4=160(cm2),即黑色部分的面积约为160cm2.
6.《数书九章》是我国南宋数学家秦九韶所著的数学著作,标志着中国古代数学的高峰.书中记载有这样一道题目:粮仓开仓收粮,有人送来米2 000石,验得米内夹谷,抽样取米一把,数得300粒米内夹谷36粒,则这批米内夹谷约为________石.
240
返回
7.某区七年级有3 000名学生参加“安全伴我行知识竞赛”活动.为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分(得分取正整数,满分为100分)进行统计.
分组(分) 频数 频率
49.5~59.5 10
59.5~69.5 16 0.08
69.5~79.5 0.20
79.5~89.5 62
89.5~100.5 72 0.36
请你根据不完整的频率分布表,解答下列问题:
(1)补全如图所示的频数直方图;
【解】补全频数直方图如图所示.
(2)若将得分转化为等级,规定得分低于59.5分评为“D”, 59.5~69.5分评为“C”, 69.5~89.5分评为“B”, 89.5~100.5分评为“A”.这次全区七年级参加竞赛的学生中约有多少名学生参赛成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩被评为“A”“B”“C”“D”哪一个等级的可能性大?请说明理由.
返回
∴P(B)>P(A)>P(C)>P(D),
∴随机抽查一名参赛学生的成绩等级,这名学生的成绩被评为“B”的可能性大.
用频率估计概率
我们可以通过大量重复试验,用一个随机事件发生的频率去估计它的概率.
频率与概率的区别与联系:
概率是确定的常数,频率是不确定的、随机的,受试验条件影响.试验次数越多,频率越趋向于概率.
课堂小结
用频率估计概率
教科书练习
布置作业
谢谢观看!
