26.2.1二次函数y=ax2的图象与性质 课件(共32张PPT)
文档属性
| 名称 | 26.2.1二次函数y=ax2的图象与性质 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览






文档简介
(共32张PPT)
26.2.1 二次函数y=ax 的
图象和性质
第26章 二次函数
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.会用描点法画出y=ax2的图象.
2.观察二次函数y=x2的图象,掌握二次函数图象的基本性质.
3.比较a取不同值时二次函数y=ax2的图象,理解系数a对二次函数图象的影响.
通过探索实际问题中数量关系的过程,体会建立二次函数模型的思想,培养学生从实际问题中抽象出数学问题的能力。
在画二次函数图象及探究其性质的过程中,培养学生的动手操作能力、观察分析能力和归纳总结能力,体会数形结合的数学思想。
情感态度与价值观目标
感受数学与生活的紧密联系,激发学生学习数学的兴趣,培养学生应用数学知识解决实际问题的意识。
在小组合作学习中,培养学生的团队协作精神和勇于探索创新的精神。
二、教学重难点
重点
二次函数的概念、表达式及图象性质。
用二次函数的知识解决实际问题。
难点
理解二次函数图象与系数之间的关系,能根据图象性质确定函数表达式中的系数。
运用二次函数解决实际问题时,如何建立合适的数学模型。
三、教学方法
讲授法:系统讲解二次函数的概念、表达式、图象性质等重要知识点,确保学生掌握基础知识。
探究法:组织学生通过小组合作探究二次函数图象的特点和性质,培养学生自主探索和合作交流的能力。
练习法:通过针对性的练习题,让学生巩固所学的二次函数知识,提高应用能力。
四、教学过程
(一)情境导入(5 分钟)
教师展示一些生活中的实际问题情境图片,如喷泉的水流轨迹、拱桥的形状等。
提问:同学们,观察这些图片,你们能发现其中的曲线有什么共同特点吗?这些曲线所代表的数学模型是什么呢?
引导学生思考并讨论,引出本节课的主题 —— 二次函数。
(二)知识新授(25 分钟)
二次函数的概念
教师给出一些具体的函数表达式,如\(y = 2x^2\),\(y = -3x^2 + 2x - 1\),\(y = \frac{1}{2}x^2\)等。
提问:观察这些函数表达式,它们有什么共同特征?
引导学生分析发现:这些函数的表达式都是整式,自变量的最高次数是 2,且二次项系数不为 0。
教师总结二次函数的定义:一般地,形如\(y = ax^2 + bx + c\)(\(a\),\(b\),\(c\)是常数,\(a\neq0\))的函数,叫做二次函数。其中\(x\)是自变量,\(a\),\(b\),\(c\)分别是函数表达式的二次项系数、一次项系数和常数项。
二次函数的表达式
教师强调二次函数的一般形式\(y = ax^2 + bx + c\)(\(a\neq0\)),并举例说明如何确定各项系数。
给出一些具体的二次函数,让学生指出其二次项系数、一次项系数和常数项。
同时介绍二次函数的特殊形式:当\(b = 0\)时,\(y = ax^2 + c\);当\(c = 0\)时,\(y = ax^2 + bx\);当\(b = c = 0\)时,\(y = ax^2\)。
二次函数的图象与性质
画二次函数\(y = x^2\)的图象
教师引导学生列表、描点、连线来画出函数\(y = x^2\)的图象。
列表:选取一些自变量\(x\)的值,计算出对应的函数值\(y\)。
描点:在平面直角坐标系中,将表中对应的点\((x,y)\)描出来。
连线:用平滑的曲线将这些点依次连接起来,得到\(y = x^2\)的图象。
探究\(y = x^2\)的图象性质
教师引导学生观察图象,提问:图象的开口方向是怎样的?图象有对称轴吗?对称轴方程是什么?图象有最高点或最低点吗?其坐标是多少?
学生观察、思考并回答问题,教师进行总结:二次函数\(y = x^2\)的图象开口向上,对称轴是\(y\)轴(即直线\(x = 0\)),图象有最低点,最低点的坐标是\((0,0)\),这个点叫做抛物线的顶点。当\(x\lt0\)时,\(y\)随\(x\)的增大而减小;当\(x\gt0\)时,\(y\)随\(x\)的增大而增大。
探究二次函数\(y = ax^2\)(\(a\neq0\))的图象性质
教师利用多媒体展示不同\(a\)值(\(a\gt0\)和\(a\lt0\))时二次函数\(y = ax^2\)的图象。
引导学生观察图象,总结\(a\)的正负对图象开口方向的影响:当\(a\gt0\)时,抛物线开口向上;当\(a\lt0\)时,抛物线开口向下。同时,\(|a|\)越大,抛物线的开口越窄;\(|a|\)越小,抛物线的开口越宽。
对于对称轴和顶点坐标,\(y = ax^2\)的对称轴始终是\(y\)轴(直线\(x = 0\)),顶点坐标是\((0,0)\)。
探究二次函数\(y = ax^2 + bx + c\)(\(a\neq0\))的图象性质
教师指出通过配方可将\(y = ax^2 + bx + c\)化为\(y = a(x - h)^2 + k\)的形式(其中\(h = -\frac{b}{2a}\),\(k = \frac{4ac - b^2}{4a}\))。
抛物线\(y = a(x - h)^2 + k\)的对称轴是直线\(x = h\),顶点坐标是\((h,k)\)。当\(a\gt0\)时,抛物线开口向上,在对称轴左侧,\(y\)随\(x\)的增大而减小;在对称轴右侧,\(y\)随\(x\)的增大而增大。当\(a\lt0\)时,抛物线开口向下,在对称轴左侧,\(y\)随\(x\)的增大而增大;在对称轴右侧,\(y\)随\(x\)的增大而减小。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究一 二次函数y=ax2的图象
活动1:类比一次函数的研究内容和研究方法,小组之间相互交流讨论,画出二次函数 y = x2 的图象.
(1)列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
探究一 二次函数y=ax2的图象
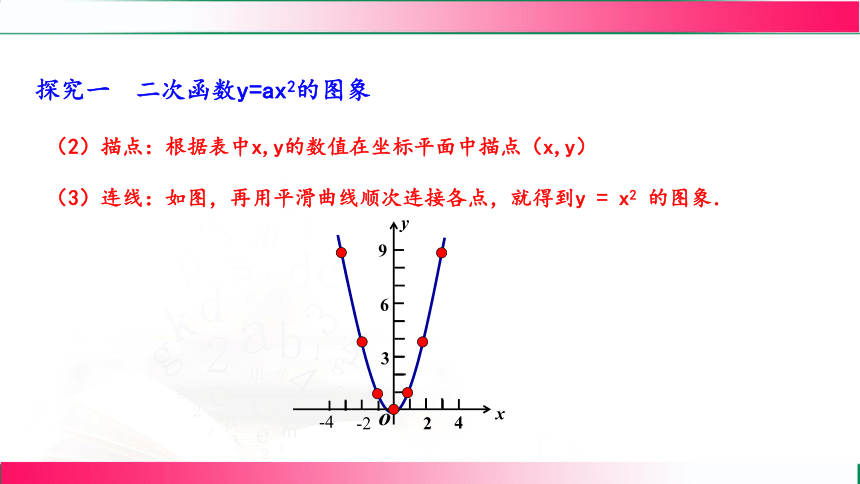
(2)描点:根据表中x,y的数值在坐标平面中描点(x,y)
(3)连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图象.
2
4
-2
-4
o
3
6
9
x
y
探究一 二次函数y=ax2的图象
-3
3
o
3
6
9
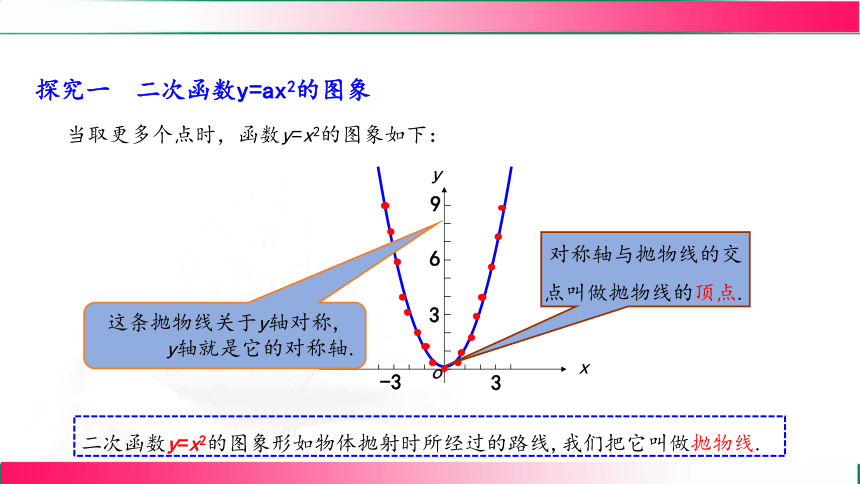
当取更多个点时,函数y=x2的图象如下:
x
y
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,
y轴就是它的对称轴.
对称轴与抛物线的交
点叫做抛物线的顶点.
探究一 二次函数y=ax2的图象
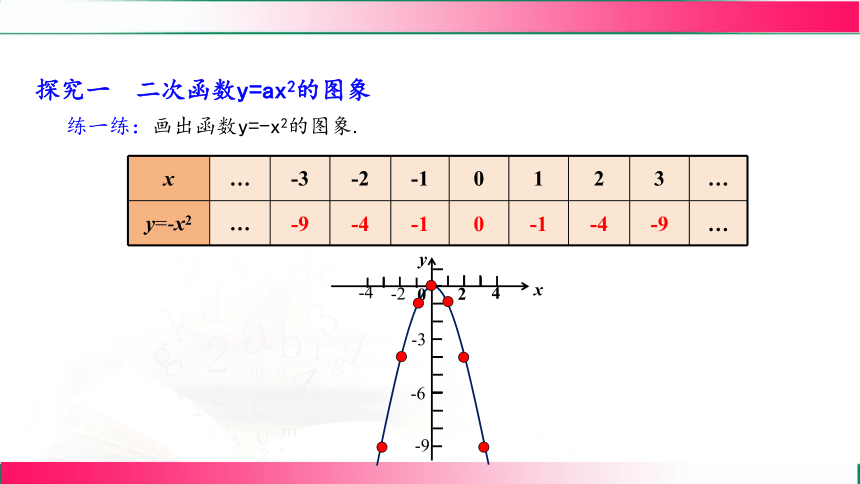
练一练:画出函数y=-x2的图象.
y
2
4
-2
-4
0
-3
-6
-9
x
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
探究一 二次函数y=ax2的图象
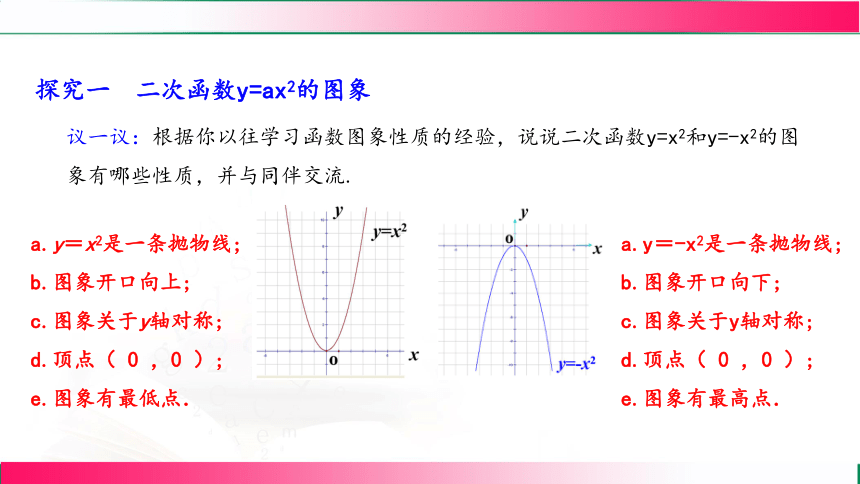
议一议:根据你以往学习函数图象性质的经验,说说二次函数y=x2和y=-x2的图象有哪些性质,并与同伴交流.
a.y=x2是一条抛物线;
b.图象开口向上;
c.图象关于y轴对称;
d.顶点( 0 ,0 );
e.图象有最低点.
a.y=-x2是一条抛物线;
b.图象开口向下;
c.图象关于y轴对称;
d.顶点( 0 ,0 );
e.图象有最高点.
探究一 二次函数y=ax2的图象
归纳总结:
1. 顶点都在原点;
3. 当a>0时,开口向上;
当a<0时,开口向下.
二次函数y=ax2 的图象性质:
2. 图象关于y轴对称;
探究一 二次函数y=ax2的图象
交流讨论
观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
x
y
O
y=ax2
y=-ax2
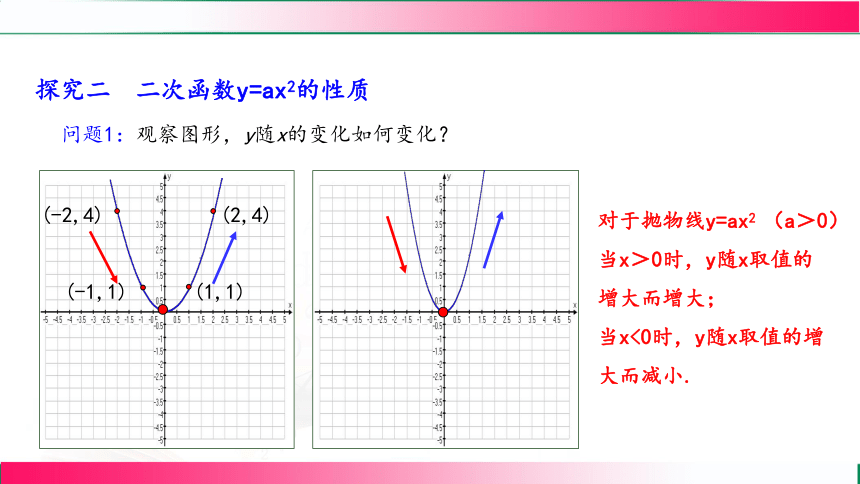
探究二 二次函数y=ax2的性质
问题1:观察图形,y随x的变化如何变化?
(-2,4)
(-1,1)
(2,4)
(1,1)
对于抛物线y=ax2 (a>0)
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
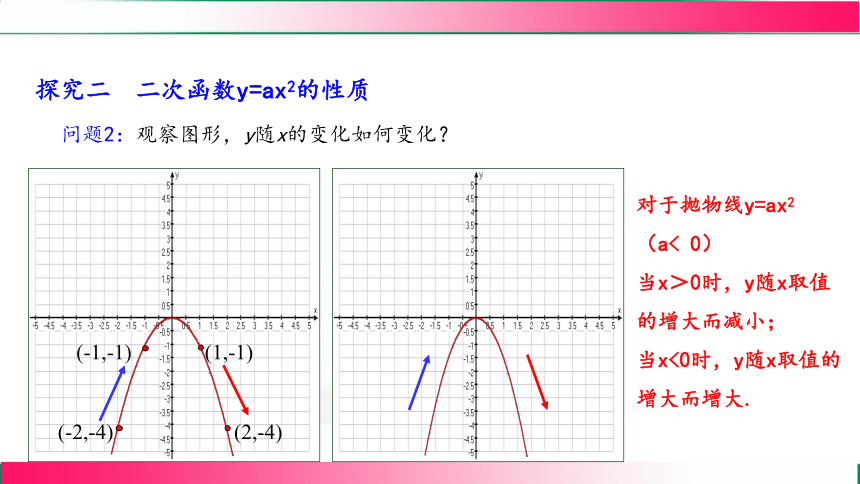
探究二 二次函数y=ax2的性质
问题2:观察图形,y随x的变化如何变化?
(-2,-4)
(-1,-1)
(2,-4)
(1,-1)
对于抛物线y=ax2
(a< 0)
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
探究二 二次函数y=ax2的性质
解:分别填表,再画出它们的图象,如图
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
例2 在同一直角坐标系中,画出函数 的图象.
探究二 二次函数y=ax2的性质
x
y
O
-2
2
2
4
6
4
-4
8
思考1:从二次函数 开口大小与a的大小有什么关系?
当a>0时,a越大,开口越小.
探究二 二次函数y=ax2的性质
x
y
O
-2
2
-2
-4
-6
4
-4
-8
当a<0时,a越小(即a的绝对值越大),开口越小.
思考2 从二次函数 开口大小与a的大小有什么关系?
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
y=ax2 a>0 a<0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
返回
D
2.抛物线y=-x2不具有的性质是( )
A.对称轴是y轴
B.开口向下
C.当x<0时,y随x的增大而减小
D.顶点坐标是(0,0)
C
返回
返回
A
3.[2024广东]若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A.y3>y2>y1 B.y2>y1>y3
C.y1>y3>y2 D.y3>y1>y2
4. 如果抛物线y=(2a-1)x2的开口向下,那么实数a的值可能是_______________.
-2(答案不唯一)
返回
5.[2024泰安泰山区期中]已知函数y=(m+2)·xm2+m-4是关于x的二次函数,当m=________时,该二次函数有最小值,最小值为________;当m=________时,在其图象的对称轴的左侧,y随着x的增大而增大.
2
0
-3
【点拨】∵函数y=(m+2)xm2+m-4是关于x的二次函数,∴m2+m-4=2且m+2≠0,解得m=2或-3.
∵该二次函数有最小值,
∴抛物线开口向上.∴m+2>0.∴m>-2.
∴m=2,此时y=4x2,最小值为0.
∵在其图象的对称轴的左侧,y随着x的增大而增大,
∴m+2<0.∴m<-2.∴m=-3.
返回
6.如图所示,三个二次函数的图象分别对应的是①y=a1x2;②y=a2x2;③y=a3x2;则a1,a2,a3的大小关系是__________.
a1>a2>a3
【点方法】抛物线的开口方向决定了a的正负性·,抛物线的开口大小决定了a的绝对值的大小·,即开口越大,|a|越小,开口越小,|a|越大.
【点拨】∵y=a1x2的图象开口小于y=a2x2的开口,且开口方向都向上,∴a1>a2>0.
∵y=a3x2的图象开口向下,∴a3<0.∴a1>a2>a3.
返回
7.已知抛物线y=ax2经过点(1,3).
(1)求a的值;
(2)当x=3时,求y的值.
【解】∵抛物线y=ax2经过点(1,3),∴a×12=3.∴a=3.
把x=3代入y=3x2中,得y=3×32=27.
返回
8.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出二次函数y=2x2与y=-2x2的图象,则阴影部分的面积是( )
A.4
B.6
C.8
D.12
返回
C
9.二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
【点拨】由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A;
当a>0时,二次函数y=ax2的图象开口向上,一次函数y=ax+a的图象经过一、二、三象限,排除B;
当a<0时,二次函数y=ax2的图象开口向下,一次函数y=ax+a的图象经过二、三、四象限,排除C.
故选D.
返回
【答案】 D
返回
【答案】 A
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
谢谢观看!
26.2.1 二次函数y=ax 的
图象和性质
第26章 二次函数
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.会用描点法画出y=ax2的图象.
2.观察二次函数y=x2的图象,掌握二次函数图象的基本性质.
3.比较a取不同值时二次函数y=ax2的图象,理解系数a对二次函数图象的影响.
通过探索实际问题中数量关系的过程,体会建立二次函数模型的思想,培养学生从实际问题中抽象出数学问题的能力。
在画二次函数图象及探究其性质的过程中,培养学生的动手操作能力、观察分析能力和归纳总结能力,体会数形结合的数学思想。
情感态度与价值观目标
感受数学与生活的紧密联系,激发学生学习数学的兴趣,培养学生应用数学知识解决实际问题的意识。
在小组合作学习中,培养学生的团队协作精神和勇于探索创新的精神。
二、教学重难点
重点
二次函数的概念、表达式及图象性质。
用二次函数的知识解决实际问题。
难点
理解二次函数图象与系数之间的关系,能根据图象性质确定函数表达式中的系数。
运用二次函数解决实际问题时,如何建立合适的数学模型。
三、教学方法
讲授法:系统讲解二次函数的概念、表达式、图象性质等重要知识点,确保学生掌握基础知识。
探究法:组织学生通过小组合作探究二次函数图象的特点和性质,培养学生自主探索和合作交流的能力。
练习法:通过针对性的练习题,让学生巩固所学的二次函数知识,提高应用能力。
四、教学过程
(一)情境导入(5 分钟)
教师展示一些生活中的实际问题情境图片,如喷泉的水流轨迹、拱桥的形状等。
提问:同学们,观察这些图片,你们能发现其中的曲线有什么共同特点吗?这些曲线所代表的数学模型是什么呢?
引导学生思考并讨论,引出本节课的主题 —— 二次函数。
(二)知识新授(25 分钟)
二次函数的概念
教师给出一些具体的函数表达式,如\(y = 2x^2\),\(y = -3x^2 + 2x - 1\),\(y = \frac{1}{2}x^2\)等。
提问:观察这些函数表达式,它们有什么共同特征?
引导学生分析发现:这些函数的表达式都是整式,自变量的最高次数是 2,且二次项系数不为 0。
教师总结二次函数的定义:一般地,形如\(y = ax^2 + bx + c\)(\(a\),\(b\),\(c\)是常数,\(a\neq0\))的函数,叫做二次函数。其中\(x\)是自变量,\(a\),\(b\),\(c\)分别是函数表达式的二次项系数、一次项系数和常数项。
二次函数的表达式
教师强调二次函数的一般形式\(y = ax^2 + bx + c\)(\(a\neq0\)),并举例说明如何确定各项系数。
给出一些具体的二次函数,让学生指出其二次项系数、一次项系数和常数项。
同时介绍二次函数的特殊形式:当\(b = 0\)时,\(y = ax^2 + c\);当\(c = 0\)时,\(y = ax^2 + bx\);当\(b = c = 0\)时,\(y = ax^2\)。
二次函数的图象与性质
画二次函数\(y = x^2\)的图象
教师引导学生列表、描点、连线来画出函数\(y = x^2\)的图象。
列表:选取一些自变量\(x\)的值,计算出对应的函数值\(y\)。
描点:在平面直角坐标系中,将表中对应的点\((x,y)\)描出来。
连线:用平滑的曲线将这些点依次连接起来,得到\(y = x^2\)的图象。
探究\(y = x^2\)的图象性质
教师引导学生观察图象,提问:图象的开口方向是怎样的?图象有对称轴吗?对称轴方程是什么?图象有最高点或最低点吗?其坐标是多少?
学生观察、思考并回答问题,教师进行总结:二次函数\(y = x^2\)的图象开口向上,对称轴是\(y\)轴(即直线\(x = 0\)),图象有最低点,最低点的坐标是\((0,0)\),这个点叫做抛物线的顶点。当\(x\lt0\)时,\(y\)随\(x\)的增大而减小;当\(x\gt0\)时,\(y\)随\(x\)的增大而增大。
探究二次函数\(y = ax^2\)(\(a\neq0\))的图象性质
教师利用多媒体展示不同\(a\)值(\(a\gt0\)和\(a\lt0\))时二次函数\(y = ax^2\)的图象。
引导学生观察图象,总结\(a\)的正负对图象开口方向的影响:当\(a\gt0\)时,抛物线开口向上;当\(a\lt0\)时,抛物线开口向下。同时,\(|a|\)越大,抛物线的开口越窄;\(|a|\)越小,抛物线的开口越宽。
对于对称轴和顶点坐标,\(y = ax^2\)的对称轴始终是\(y\)轴(直线\(x = 0\)),顶点坐标是\((0,0)\)。
探究二次函数\(y = ax^2 + bx + c\)(\(a\neq0\))的图象性质
教师指出通过配方可将\(y = ax^2 + bx + c\)化为\(y = a(x - h)^2 + k\)的形式(其中\(h = -\frac{b}{2a}\),\(k = \frac{4ac - b^2}{4a}\))。
抛物线\(y = a(x - h)^2 + k\)的对称轴是直线\(x = h\),顶点坐标是\((h,k)\)。当\(a\gt0\)时,抛物线开口向上,在对称轴左侧,\(y\)随\(x\)的增大而减小;在对称轴右侧,\(y\)随\(x\)的增大而增大。当\(a\lt0\)时,抛物线开口向下,在对称轴左侧,\(y\)随\(x\)的增大而增大;在对称轴右侧,\(y\)随\(x\)的增大而减小。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究一 二次函数y=ax2的图象
活动1:类比一次函数的研究内容和研究方法,小组之间相互交流讨论,画出二次函数 y = x2 的图象.
(1)列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
探究一 二次函数y=ax2的图象
(2)描点:根据表中x,y的数值在坐标平面中描点(x,y)
(3)连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图象.
2
4
-2
-4
o
3
6
9
x
y
探究一 二次函数y=ax2的图象
-3
3
o
3
6
9
当取更多个点时,函数y=x2的图象如下:
x
y
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,
y轴就是它的对称轴.
对称轴与抛物线的交
点叫做抛物线的顶点.
探究一 二次函数y=ax2的图象
练一练:画出函数y=-x2的图象.
y
2
4
-2
-4
0
-3
-6
-9
x
x … -3 -2 -1 0 1 2 3 …
y=-x2 … -9 -4 -1 0 -1 -4 -9 …
探究一 二次函数y=ax2的图象
议一议:根据你以往学习函数图象性质的经验,说说二次函数y=x2和y=-x2的图象有哪些性质,并与同伴交流.
a.y=x2是一条抛物线;
b.图象开口向上;
c.图象关于y轴对称;
d.顶点( 0 ,0 );
e.图象有最低点.
a.y=-x2是一条抛物线;
b.图象开口向下;
c.图象关于y轴对称;
d.顶点( 0 ,0 );
e.图象有最高点.
探究一 二次函数y=ax2的图象
归纳总结:
1. 顶点都在原点;
3. 当a>0时,开口向上;
当a<0时,开口向下.
二次函数y=ax2 的图象性质:
2. 图象关于y轴对称;
探究一 二次函数y=ax2的图象
交流讨论
观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
x
y
O
y=ax2
y=-ax2
探究二 二次函数y=ax2的性质
问题1:观察图形,y随x的变化如何变化?
(-2,4)
(-1,1)
(2,4)
(1,1)
对于抛物线y=ax2 (a>0)
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
探究二 二次函数y=ax2的性质
问题2:观察图形,y随x的变化如何变化?
(-2,-4)
(-1,-1)
(2,-4)
(1,-1)
对于抛物线y=ax2
(a< 0)
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
探究二 二次函数y=ax2的性质
解:分别填表,再画出它们的图象,如图
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
例2 在同一直角坐标系中,画出函数 的图象.
探究二 二次函数y=ax2的性质
x
y
O
-2
2
2
4
6
4
-4
8
思考1:从二次函数 开口大小与a的大小有什么关系?
当a>0时,a越大,开口越小.
探究二 二次函数y=ax2的性质
x
y
O
-2
2
-2
-4
-6
4
-4
-8
当a<0时,a越小(即a的绝对值越大),开口越小.
思考2 从二次函数 开口大小与a的大小有什么关系?
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
y=ax2 a>0 a<0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
返回
D
2.抛物线y=-x2不具有的性质是( )
A.对称轴是y轴
B.开口向下
C.当x<0时,y随x的增大而减小
D.顶点坐标是(0,0)
C
返回
返回
A
3.[2024广东]若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A.y3>y2>y1 B.y2>y1>y3
C.y1>y3>y2 D.y3>y1>y2
4. 如果抛物线y=(2a-1)x2的开口向下,那么实数a的值可能是_______________.
-2(答案不唯一)
返回
5.[2024泰安泰山区期中]已知函数y=(m+2)·xm2+m-4是关于x的二次函数,当m=________时,该二次函数有最小值,最小值为________;当m=________时,在其图象的对称轴的左侧,y随着x的增大而增大.
2
0
-3
【点拨】∵函数y=(m+2)xm2+m-4是关于x的二次函数,∴m2+m-4=2且m+2≠0,解得m=2或-3.
∵该二次函数有最小值,
∴抛物线开口向上.∴m+2>0.∴m>-2.
∴m=2,此时y=4x2,最小值为0.
∵在其图象的对称轴的左侧,y随着x的增大而增大,
∴m+2<0.∴m<-2.∴m=-3.
返回
6.如图所示,三个二次函数的图象分别对应的是①y=a1x2;②y=a2x2;③y=a3x2;则a1,a2,a3的大小关系是__________.
a1>a2>a3
【点方法】抛物线的开口方向决定了a的正负性·,抛物线的开口大小决定了a的绝对值的大小·,即开口越大,|a|越小,开口越小,|a|越大.
【点拨】∵y=a1x2的图象开口小于y=a2x2的开口,且开口方向都向上,∴a1>a2>0.
∵y=a3x2的图象开口向下,∴a3<0.∴a1>a2>a3.
返回
7.已知抛物线y=ax2经过点(1,3).
(1)求a的值;
(2)当x=3时,求y的值.
【解】∵抛物线y=ax2经过点(1,3),∴a×12=3.∴a=3.
把x=3代入y=3x2中,得y=3×32=27.
返回
8.如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出二次函数y=2x2与y=-2x2的图象,则阴影部分的面积是( )
A.4
B.6
C.8
D.12
返回
C
9.二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
【点拨】由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A;
当a>0时,二次函数y=ax2的图象开口向上,一次函数y=ax+a的图象经过一、二、三象限,排除B;
当a<0时,二次函数y=ax2的图象开口向下,一次函数y=ax+a的图象经过二、三、四象限,排除C.
故选D.
返回
【答案】 D
返回
【答案】 A
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
谢谢观看!
