26.3.2 实践与探索 课件(共25张PPT)
文档属性
| 名称 | 26.3.2 实践与探索 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
26.3.2 实践与探索
第26章 二次函数
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解二次函数与一元二次方程之间的联系
2.知道二次函数的图象与x轴的交点个数与一元二次方程的根的个数之间的关系
3.了解用图象法求一元二次方程的近似解
通过探索实际问题中数量关系的过程,体会建立二次函数模型的思想,培养学生从实际问题中抽象出数学问题的能力。
在画二次函数图象及探究其性质的过程中,培养学生的动手操作能力、观察分析能力和归纳总结能力,体会数形结合的数学思想。
情感态度与价值观目标
感受数学与生活的紧密联系,激发学生学习数学的兴趣,培养学生应用数学知识解决实际问题的意识。
在小组合作学习中,培养学生的团队协作精神和勇于探索创新的精神。
二、教学重难点向上,在对称轴左侧,\(y\)随\(x\)的增大而减小;在对称轴右侧,\(y\)随\(x\)的增大而增大。当\(a\lt0\)时,抛物线开口向下,在对称轴左侧,\(y\)随\(x\)的增大而增大;在对称轴右侧,\(y\)随\(x\)的增大而减小。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
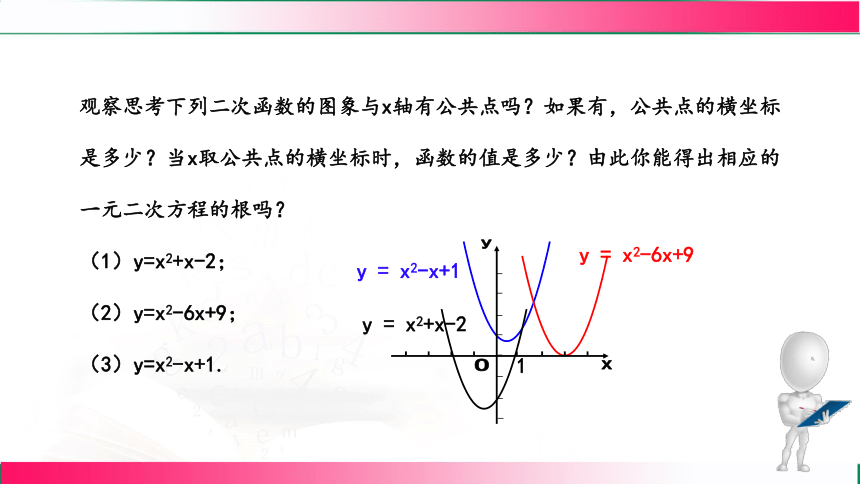
观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标
是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的
一元二次方程的根吗?
(1)y=x2+x-2;
(2)y=x2-6x+9;
(3)y=x2-x+1.
1
x
y
O
y = x2-6x+9
y = x2-x+1
y = x2+x-2
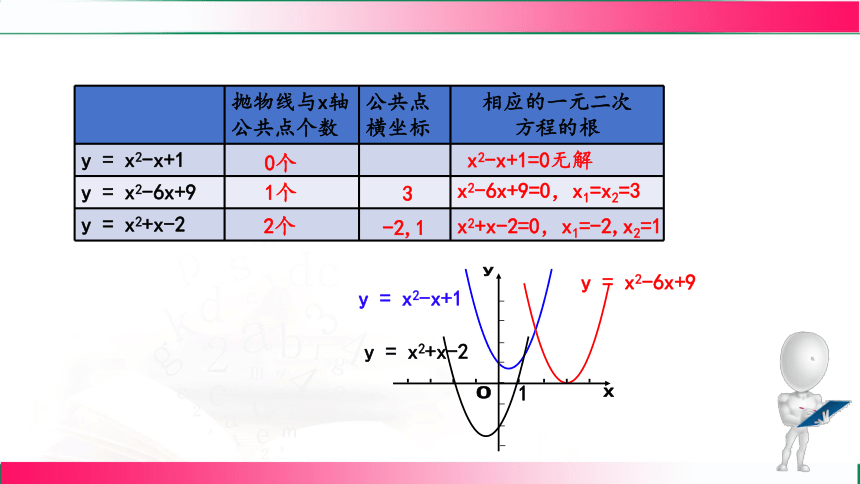
抛物线与x轴公共点个数 公共点 横坐标 相应的一元二次
方程的根
y = x2-x+1
y = x2-6x+9
y = x2+x-2
0个
1个
2个
x2-x+1=0无解
3
x2-6x+9=0,x1=x2=3
-2,1
x2+x-2=0,x1=-2,x2=1
1
x
y
O
y = x2-6x+9
y = x2-x+1
y = x2+x-2
二次函数y=ax2+bx+c 的图象与x轴交点 一元二次方程ax2+bx+c=0的根 b2-4ac
有两个交点
有一个交点
没有交点
归纳总结
有两个不相等的实数根
b2-4ac>0
有两个相等的实数根
b2-4ac=0
没有实数根
b2-4ac<0
例1.已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:当m≠2时,此抛物线与x轴总有两个交点;
证明:∵m≠0,
∴当m≠2时,此抛物线与x轴总有两个交点.
∴Δ≥0,
∵(m-2)2≥0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∴mx2-(m+2)x+2=0是一元二次方程,
例1.已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是正整数,求整数m的值.
解:令y=0,则mx2-(m+2)x+2=0,
则x2=1(舍去)或2;
依题意有:x2是正整数,m为整数,
解得 x1=1,x2= ;
即(x-1)(mx-2)=0,
∴当x2=2时,m=1,
故整数m为1.
例2.求一元二次方程x2-2x-1=0的根的近似值(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点
的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交
点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个
实数根,一个在-1与0之间,另一个在2与3之间.
取-1,0的平均数-0.5,x=-0.5时,y=0.25>0;
取-0.5,0的平均数-0.25,x=-0.25时,y=-0.4<0;
取-0.5,-0.25的平均数-0.375,y=-0.11<0;
∴一个根处于-0.5与-0.4之间,且x=-0.4时,y更靠近0;
∴x1≈-0.4,
同理:x2≈2.4.
又因为结果精确到0.1,故直接取-0.4,x=-0.4时,y=-0.04<0;
归纳总结
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 y=ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解.
利用二次函数的图象求一元二次方程的ax2+bx+c=0的近似根;
1. 抛物线y=-3x2-x+4与x轴的交点有( )
A.0个 B.1个 C.2个 D.3个
C
[变式][2024长春]若抛物线y=x2-x+c(c是常数)与x轴没有交点,则c的取值范围是________.
【点方法】二次函数y=ax2+bx+c,当b2-4ac>0时,图象与x轴有两个交点;当b2-4ac=0时,图象与x轴有一个交点;当b2-4ac<0时,图象与x轴没有交点.
返回
2. [教材P29做一做] 二次函数y=ax2+bx+c的部分图象如图所示,关于x的一元二次方程ax2+bx+c=0的解为( )
A.x1=-4,x2=2
B.x1=-3,x2=-1
C.x1=-4,x2=-2
D.x1=-2,x2=2
A
返回
返回
C
3. 如图,抛物线y=ax2+bx+c的部分图象与x轴交于点(3,0),对称轴为直线x=1,对于整个抛物线来说,当y≤0时,x的取值范围是( )
A.0<x≤3
B.-2≤x≤3
C.-1≤x≤3
D.x≤-1或x≥3
4.[2024杭州月考]下表给出了二次函数y=ax2+bx+c(a≠0)中x,y的一些对应值,则可以估计一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围为( )
A.0.6<x1<0.7 B.0.7<x1<0.8
C.0.8<x1<0.9 D.0.9<x1<1
B
返回
x … 0.6 0.7 0.8 0.9 1 …
y … -0.44 -0.11 0.24 0.61 1 …
5.[2024信阳月考]如图,将二次函数y=x2-4位于x轴下方的图象沿x轴翻折,得到一个新函数的图象(图中的实线).
返回
(1)当x=-3时,新函数值为________,当x=1时,新函数值为________;
(2)当x=________时,新函数有最小值;
(3)当新函数中函数值y随x的增大而增大时,自变量x的取值范围是________________;
(4)若直线y=a与新函数的图象有两个公共点,则a的取值范围是____________.
5
3
-2或2
-2<x<0或x>2
a>4或a=0
6.[2024宜春期中]二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)求该二次函数的表达式;
【解】由题图知该二次函数的图象与x轴的交点坐标为(1,0)和(3,0),顶点坐标为(2,-2),
∴可设该二次函数的表达式为y=a(x-2)2-2.
把(1,0)的坐标代入上式,得0=a(1-2)2-2,解得a=2.
∴该二次函数的表达式为y=2(x-2)2-2=2x2-8x+6.
(2)直接写出不等式ax2+bx+c>0的解集;
【解】由函数图象可知不等式ax2+bx+c>0的解集为x<1或x>3.
返回
(3)若方程ax2+bx+c=k有两个不相等的实数根,直接写出k的取值范围.
【解】k>-2
7. 将抛物线y=2x2-12x+22绕点(5,2)旋转180°后得到的新抛物线与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
判别式 △>0 △=0 △<0
二次函数y=ax2+bx+c (a>0)的图象
ax2+bx+c=0 (a≠0)的根
ax2+bx+c>0 (a>0)的解集
ax2+bx+c<0 (a>0)的解集
x1 ; x2
x1 =x2
没有实数根
x2
x1
x
y
O
x1= x2
x
y
x
O
y
x<x1或x>x2
x≠x1的一切实数
所有实数
x1<x<x2
无解
无解
谢谢观看!
26.3.2 实践与探索
第26章 二次函数
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解二次函数与一元二次方程之间的联系
2.知道二次函数的图象与x轴的交点个数与一元二次方程的根的个数之间的关系
3.了解用图象法求一元二次方程的近似解
通过探索实际问题中数量关系的过程,体会建立二次函数模型的思想,培养学生从实际问题中抽象出数学问题的能力。
在画二次函数图象及探究其性质的过程中,培养学生的动手操作能力、观察分析能力和归纳总结能力,体会数形结合的数学思想。
情感态度与价值观目标
感受数学与生活的紧密联系,激发学生学习数学的兴趣,培养学生应用数学知识解决实际问题的意识。
在小组合作学习中,培养学生的团队协作精神和勇于探索创新的精神。
二、教学重难点向上,在对称轴左侧,\(y\)随\(x\)的增大而减小;在对称轴右侧,\(y\)随\(x\)的增大而增大。当\(a\lt0\)时,抛物线开口向下,在对称轴左侧,\(y\)随\(x\)的增大而增大;在对称轴右侧,\(y\)随\(x\)的增大而减小。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标
是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的
一元二次方程的根吗?
(1)y=x2+x-2;
(2)y=x2-6x+9;
(3)y=x2-x+1.
1
x
y
O
y = x2-6x+9
y = x2-x+1
y = x2+x-2
抛物线与x轴公共点个数 公共点 横坐标 相应的一元二次
方程的根
y = x2-x+1
y = x2-6x+9
y = x2+x-2
0个
1个
2个
x2-x+1=0无解
3
x2-6x+9=0,x1=x2=3
-2,1
x2+x-2=0,x1=-2,x2=1
1
x
y
O
y = x2-6x+9
y = x2-x+1
y = x2+x-2
二次函数y=ax2+bx+c 的图象与x轴交点 一元二次方程ax2+bx+c=0的根 b2-4ac
有两个交点
有一个交点
没有交点
归纳总结
有两个不相等的实数根
b2-4ac>0
有两个相等的实数根
b2-4ac=0
没有实数根
b2-4ac<0
例1.已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:当m≠2时,此抛物线与x轴总有两个交点;
证明:∵m≠0,
∴当m≠2时,此抛物线与x轴总有两个交点.
∴Δ≥0,
∵(m-2)2≥0,
∴Δ=(m+2)2-4m×2=m2+4m+4-8m=(m-2)2.
∴mx2-(m+2)x+2=0是一元二次方程,
例1.已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是正整数,求整数m的值.
解:令y=0,则mx2-(m+2)x+2=0,
则x2=1(舍去)或2;
依题意有:x2是正整数,m为整数,
解得 x1=1,x2= ;
即(x-1)(mx-2)=0,
∴当x2=2时,m=1,
故整数m为1.
例2.求一元二次方程x2-2x-1=0的根的近似值(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点
的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交
点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个
实数根,一个在-1与0之间,另一个在2与3之间.
取-1,0的平均数-0.5,x=-0.5时,y=0.25>0;
取-0.5,0的平均数-0.25,x=-0.25时,y=-0.4<0;
取-0.5,-0.25的平均数-0.375,y=-0.11<0;
∴一个根处于-0.5与-0.4之间,且x=-0.4时,y更靠近0;
∴x1≈-0.4,
同理:x2≈2.4.
又因为结果精确到0.1,故直接取-0.4,x=-0.4时,y=-0.04<0;
归纳总结
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 y=ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解.
利用二次函数的图象求一元二次方程的ax2+bx+c=0的近似根;
1. 抛物线y=-3x2-x+4与x轴的交点有( )
A.0个 B.1个 C.2个 D.3个
C
[变式][2024长春]若抛物线y=x2-x+c(c是常数)与x轴没有交点,则c的取值范围是________.
【点方法】二次函数y=ax2+bx+c,当b2-4ac>0时,图象与x轴有两个交点;当b2-4ac=0时,图象与x轴有一个交点;当b2-4ac<0时,图象与x轴没有交点.
返回
2. [教材P29做一做] 二次函数y=ax2+bx+c的部分图象如图所示,关于x的一元二次方程ax2+bx+c=0的解为( )
A.x1=-4,x2=2
B.x1=-3,x2=-1
C.x1=-4,x2=-2
D.x1=-2,x2=2
A
返回
返回
C
3. 如图,抛物线y=ax2+bx+c的部分图象与x轴交于点(3,0),对称轴为直线x=1,对于整个抛物线来说,当y≤0时,x的取值范围是( )
A.0<x≤3
B.-2≤x≤3
C.-1≤x≤3
D.x≤-1或x≥3
4.[2024杭州月考]下表给出了二次函数y=ax2+bx+c(a≠0)中x,y的一些对应值,则可以估计一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围为( )
A.0.6<x1<0.7 B.0.7<x1<0.8
C.0.8<x1<0.9 D.0.9<x1<1
B
返回
x … 0.6 0.7 0.8 0.9 1 …
y … -0.44 -0.11 0.24 0.61 1 …
5.[2024信阳月考]如图,将二次函数y=x2-4位于x轴下方的图象沿x轴翻折,得到一个新函数的图象(图中的实线).
返回
(1)当x=-3时,新函数值为________,当x=1时,新函数值为________;
(2)当x=________时,新函数有最小值;
(3)当新函数中函数值y随x的增大而增大时,自变量x的取值范围是________________;
(4)若直线y=a与新函数的图象有两个公共点,则a的取值范围是____________.
5
3
-2或2
-2<x<0或x>2
a>4或a=0
6.[2024宜春期中]二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)求该二次函数的表达式;
【解】由题图知该二次函数的图象与x轴的交点坐标为(1,0)和(3,0),顶点坐标为(2,-2),
∴可设该二次函数的表达式为y=a(x-2)2-2.
把(1,0)的坐标代入上式,得0=a(1-2)2-2,解得a=2.
∴该二次函数的表达式为y=2(x-2)2-2=2x2-8x+6.
(2)直接写出不等式ax2+bx+c>0的解集;
【解】由函数图象可知不等式ax2+bx+c>0的解集为x<1或x>3.
返回
(3)若方程ax2+bx+c=k有两个不相等的实数根,直接写出k的取值范围.
【解】k>-2
7. 将抛物线y=2x2-12x+22绕点(5,2)旋转180°后得到的新抛物线与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
判别式 △>0 △=0 △<0
二次函数y=ax2+bx+c (a>0)的图象
ax2+bx+c=0 (a≠0)的根
ax2+bx+c>0 (a>0)的解集
ax2+bx+c<0 (a>0)的解集
x1 ; x2
x1 =x2
没有实数根
x2
x1
x
y
O
x1= x2
x
y
x
O
y
x<x1或x>x2
x≠x1的一切实数
所有实数
x1<x<x2
无解
无解
谢谢观看!
