27.1.1 圆的基本元素 课件(共25张PPT)
文档属性
| 名称 | 27.1.1 圆的基本元素 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 17:40:09 | ||
图片预览





文档简介
(共25张PPT)
27.1.1 圆的基本元素
第27章 圆
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.认识圆,理解圆的本质属性.(重点)
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
教学重点
圆的定义及圆的基本元素的概念,尤其是帮助学生区分相似概念,如弦与直径、优弧与劣弧等。
同圆或等圆中半径相等这一性质的理解和应用,通过多样化的例题让学生熟练掌握该性质在不同情境下的运用。
教学难点
对圆的集合定义的深入理解,通过具体的点的位置判断、动态演示等方式,让学生教师亲自用圆规在黑板上规范地画一个圆,边画边详细讲解圆的形成过程:把圆规的一个脚稳稳地固定在一点,这一点就是圆心,另一个脚绕着这个固定点缓缓旋转一周,所划过的轨迹就形成了一个圆。
给出圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
强调圆的两个关键要素:圆心确定圆的位置,就如同我们确定一个城市在地图上的位置;半径确定圆的大小,半径越长,圆就越大,反之则越小。
进行互动提问:根据圆的定义,同学们想一想,平面内到点 O 的距离等于线段 OA 长度的点都在圆上吗?圆上的点到圆心 O 的距离都等于半径 OA 的长度吗?让学生同桌之间相互讨论,然后请几位同学发表自己的观点。
引导学生得出圆的集合定义:平面内到定点的距离等于定长的所有点组成的图形叫做圆。其中,定点称为圆心,定长称为半径。为了帮助学生理解,可举例说明,如以学校为圆心,以 1 千米为半径,那么距离学校 1 千米的所有地点就构成了一个圆。
圆的基本元素
弦:连接圆上任意两点的线段叫做弦。教师在黑板上画出一个圆,并连接圆上两点形成弦,如线段 AB、BC 都是⊙O 中的弦。同时提问学生,能否在圆上再找出其他弦。
直径:经过圆心的弦叫做直径。在圆中画出一条直径,如线段 AB 就是⊙O 的直径,强调直径是圆中最长的弦,且直径等于半径的 2 倍,即 d = 2r(d 表示直径,r 表示半径)。通过具体的半径数值,让学生计算对应的直径,加深理解。真正领会平面内到定点的距离等于定长的所有点组成的图形叫做圆。
灵活运用圆的基本元素的性质解决综合性相关问题,通过逐步引导和练习,提升学生分析问题和解决问题的能力。
三、教学方法
讲授法:以清晰、准确且生动的语言,向学生系统讲解圆的定义、基本元素的概念及相关性质,确保学生扎实掌握基础知识。在讲解过程中,注重概念的引入和解释,让学生理解知识的来龙去脉。
直观演示法:充分利用多媒体课件、圆规、直尺等工具,通过动态演示、实物操作等方式,直观展示圆的形成过程、各基本元素的特征,帮助学生建立直观且深刻的认识。例如用动画展示圆的集合定义的形成过程。
小组合作探究法:精心组织学生进行小组讨论和合作探究活动,设置有启发性的问题,让学生在交流互动中深化对圆的基本元素的理解,培养学生的合作能力和探究精神。如让小组探究同圆中不同弦长与圆心距离的关系。
练习巩固法:设计针对性强、层次分明的练习题,从基础到提高再到拓展,让学生及时巩固所学知识,逐步提高学生运用知识解决问题的能力。同时,在练习过程中及时反馈和指导,帮助学生查漏补缺。
问题引导法:在教学过程中,适时提出有思考价值的问题,引导学生主动思考、积极探索,培养学生的思维能力。如在讲解圆的基本元素时,提问学生生活中哪些现象可以用这些元素来解释。
四、教学过程
(一)导入新课(5 分钟)
运用多媒体展示生活中各种含有圆的精美图片,如车轮、摩天轮、圆形餐盘、奥运五环等,同时播放一些与圆相关的动态视频,如旋转的风扇、滚动的篮球等。
提问:同学们,在我们五彩斑斓的生活中,圆无处不在。大家仔细观察这些图片和视频,开动脑筋想一想,为什么车轮要做成圆形,而不是三角形、方形等其他形状呢?圆形的车轮在滚动过程中有什么独特的优势呢?
鼓励学生大胆发言,分享自己的想法,然后引导学生进行简单的讨论和交流,引发学生对圆的强烈好奇心和探究欲望,从而自然地引出本节课的课题 —— 圆的基本元素。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
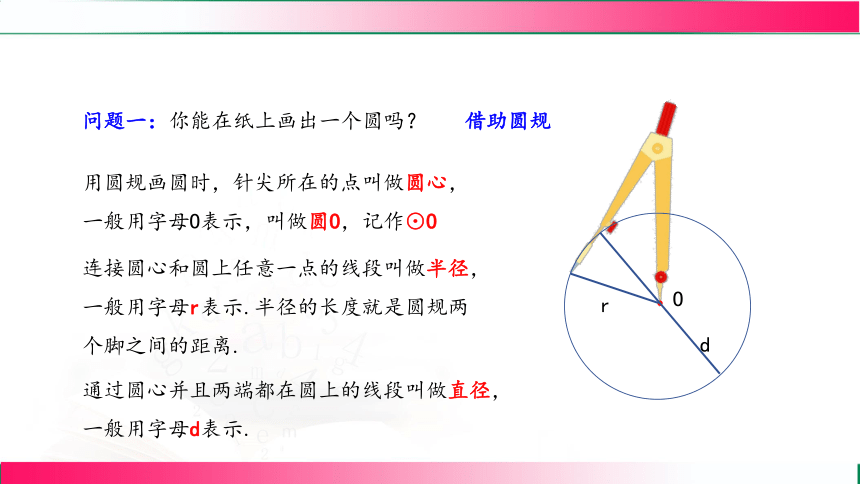
问题一:你能在纸上画出一个圆吗?
借助圆规
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示,叫做圆O,记作⊙O
O
连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示.半径的长度就是圆规两个脚之间的距离.
r
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示.
d
问题二:(1)根据借助圆规的画图过程,你知道什么是确定圆的要素吗?
一是圆心,圆心确定其位置;
二是半径,半径确定其大小.
(2)若有两个圆的半径相等,这两个圆有什么关系呢?
互为等圆;
(3)若有两个圆的半径相等,圆心的位置也相等,这两个圆有什么关系呢?
互为同圆;
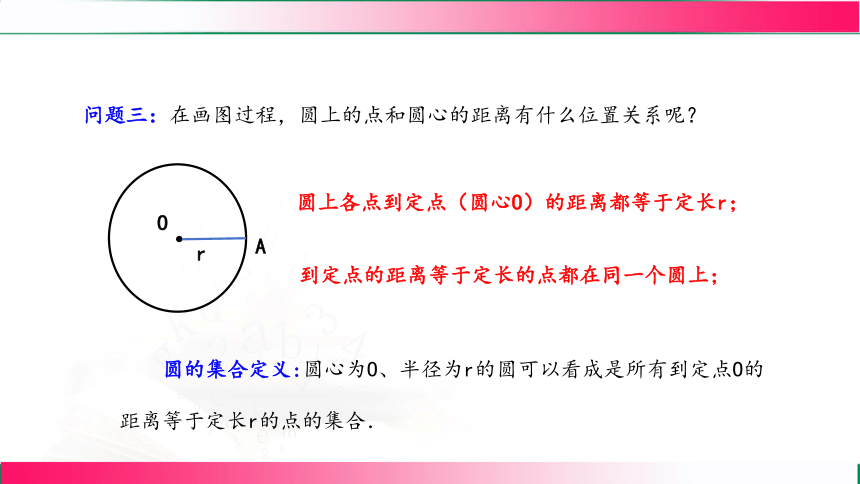
问题三:在画图过程,圆上的点和圆心的距离有什么位置关系呢?
圆上各点到定点(圆心O)的距离都等于定长r;
到定点的距离等于定长的点都在同一个圆上;
圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
A
O
r
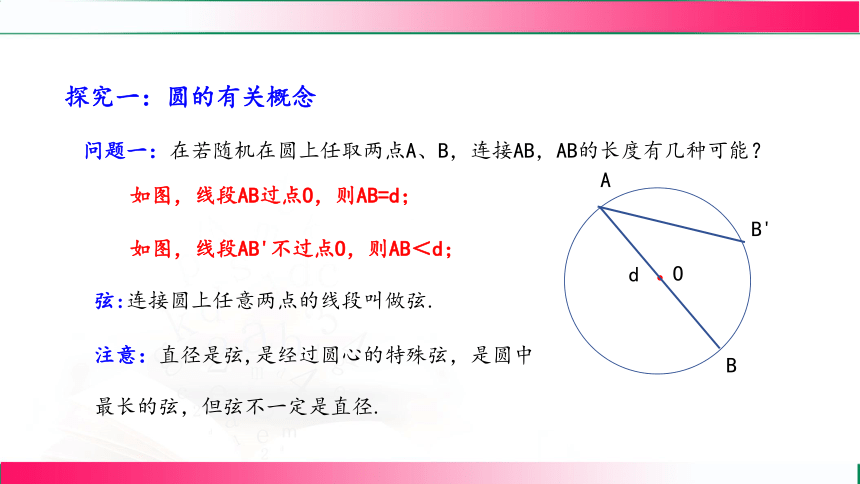
问题一:在若随机在圆上任取两点A、B,连接AB,AB的长度有几种可能?
如图,线段AB过点O,则AB=d;
如图,线段AB'不过点O,则AB<d;
弦:连接圆上任意两点的线段叫做弦.
O
d
A
B'
B
注意:直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
探究一:圆的有关概念
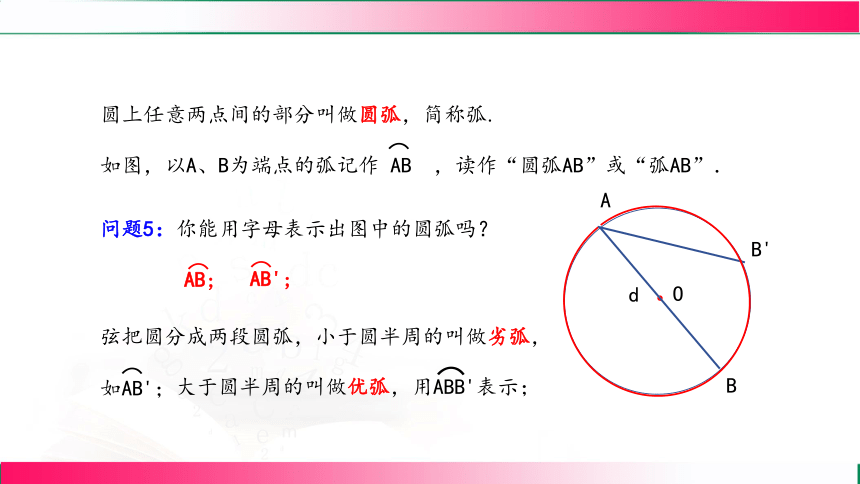
圆上任意两点间的部分叫做圆弧,简称弧.
O
d
A
B'
B
问题5:你能用字母表示出图中的圆弧吗?
如图,以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
AB;
(
AB';
(
弦把圆分成两段圆弧,小于圆半周的叫做劣弧,如AB';
(
大于圆半周的叫做优弧,用ABB'表示;
(
探究二:圆心角
问题1:(1)你能在下图中找到几个角?
O
B
A
∠AOB;
∠ABO;
∠BAO;
(3)OA、OB、AB分别与圆有什么位置关系?
OA、OB分别是圆O的半径;
AB是圆O的弦;
(2)∠AOB在圆O上有什么位置特点?
∠AOB顶点在圆心,角的两边与圆相交
O
B
A
圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角,如∠AOB .
圆心角∠AOB所对的弦为AB.
圆心角∠AOB所对的弧为AB.
⌒
归纳总结
返回
1. “车轮为什么都做成圆形?”下面解释最合理的是( )
A.圆形是轴对称图形
B.圆形特别美观大方
C.圆形是曲线图形
D.从圆心到圆上任意一点的距离都相等
D
2.已知⊙O的半径是4 cm,则⊙O中最长的弦长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
C
返回
返回
120°
3.如图,A,B是⊙O上两个点,若∠OAB=30°,则∠AOB=________.
4.如图,在⊙O中,弦有________,直径是________,优弧有____________,劣弧有____________.
AC,AB
返回
AB
5.以定点O为圆心,定长a为半径,回答问题:
(1)这样的圆可以作________个;
(2)圆心可以确定圆的________;
(3)半径可以确定圆的________;
(4)圆将平面分为________部分,分别称为圆________,圆的________,圆的________.
返回
1
位置
大小
三
圆周
外部
内部
6.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过点B作OC的平行线交OD于点E,则EO+EB=________.
2
【点拨】∵⊙O的周长为4π,
∴⊙O的半径为2,即OD=2.
∵OC=OD,∴∠C=∠D.
∵BE∥OC,∴∠EBD=∠C,∴∠EBD=∠D.
∴BE=DE,∴EO+EB=EO+DE=OD=2.
返回
7.如图,点A,B,C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
【证明】连结OA,OC,AC,如图.
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO.
∵BO平分∠ABC,∴∠ABO=∠CBO.
∴∠BAO=∠BCO.
∵OA=OC,∴∠OAC=∠OCA.
∴∠BAO+∠OAC=∠BCO+∠OCA,
即∠BAC=∠BCA.∴AB=BC.
返回
8.[2024绥化期末]下列说法:
①弦是直径;
②半圆是弧;
③过圆心的线段是直径;
④圆心相同半径相同的两个圆是同心圆,
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
返回
C
9.如图,点A,D,G,M在半圆O上,四边形ABOC,四边形DEOF,四边形HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
A.a>b>c
B.c>a>b
C.a=b=c
D.b>c>a
【点拨】如图,连结OM,OD,OA.根据矩形的对角线相等,得BC=OA,EF=OD,NH=OM.再根据同圆的半径相等,得a=b=c.故选C.
【答案】 C
[变式]如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为________.
5
弦:连接圆上任意两点的线段叫做弦.
圆弧:圆上任意两点间的部分叫做圆弧,简称弧.
小于圆半周的叫做劣弧;
大于圆半周的叫做优弧;
圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角.
谢谢观看!
27.1.1 圆的基本元素
第27章 圆
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.认识圆,理解圆的本质属性.(重点)
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
教学重点
圆的定义及圆的基本元素的概念,尤其是帮助学生区分相似概念,如弦与直径、优弧与劣弧等。
同圆或等圆中半径相等这一性质的理解和应用,通过多样化的例题让学生熟练掌握该性质在不同情境下的运用。
教学难点
对圆的集合定义的深入理解,通过具体的点的位置判断、动态演示等方式,让学生教师亲自用圆规在黑板上规范地画一个圆,边画边详细讲解圆的形成过程:把圆规的一个脚稳稳地固定在一点,这一点就是圆心,另一个脚绕着这个固定点缓缓旋转一周,所划过的轨迹就形成了一个圆。
给出圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆。固定的端点 O 叫做圆心,线段 OA 叫做半径。以点 O 为圆心的圆,记作 “⊙O”,读作 “圆 O”。
强调圆的两个关键要素:圆心确定圆的位置,就如同我们确定一个城市在地图上的位置;半径确定圆的大小,半径越长,圆就越大,反之则越小。
进行互动提问:根据圆的定义,同学们想一想,平面内到点 O 的距离等于线段 OA 长度的点都在圆上吗?圆上的点到圆心 O 的距离都等于半径 OA 的长度吗?让学生同桌之间相互讨论,然后请几位同学发表自己的观点。
引导学生得出圆的集合定义:平面内到定点的距离等于定长的所有点组成的图形叫做圆。其中,定点称为圆心,定长称为半径。为了帮助学生理解,可举例说明,如以学校为圆心,以 1 千米为半径,那么距离学校 1 千米的所有地点就构成了一个圆。
圆的基本元素
弦:连接圆上任意两点的线段叫做弦。教师在黑板上画出一个圆,并连接圆上两点形成弦,如线段 AB、BC 都是⊙O 中的弦。同时提问学生,能否在圆上再找出其他弦。
直径:经过圆心的弦叫做直径。在圆中画出一条直径,如线段 AB 就是⊙O 的直径,强调直径是圆中最长的弦,且直径等于半径的 2 倍,即 d = 2r(d 表示直径,r 表示半径)。通过具体的半径数值,让学生计算对应的直径,加深理解。真正领会平面内到定点的距离等于定长的所有点组成的图形叫做圆。
灵活运用圆的基本元素的性质解决综合性相关问题,通过逐步引导和练习,提升学生分析问题和解决问题的能力。
三、教学方法
讲授法:以清晰、准确且生动的语言,向学生系统讲解圆的定义、基本元素的概念及相关性质,确保学生扎实掌握基础知识。在讲解过程中,注重概念的引入和解释,让学生理解知识的来龙去脉。
直观演示法:充分利用多媒体课件、圆规、直尺等工具,通过动态演示、实物操作等方式,直观展示圆的形成过程、各基本元素的特征,帮助学生建立直观且深刻的认识。例如用动画展示圆的集合定义的形成过程。
小组合作探究法:精心组织学生进行小组讨论和合作探究活动,设置有启发性的问题,让学生在交流互动中深化对圆的基本元素的理解,培养学生的合作能力和探究精神。如让小组探究同圆中不同弦长与圆心距离的关系。
练习巩固法:设计针对性强、层次分明的练习题,从基础到提高再到拓展,让学生及时巩固所学知识,逐步提高学生运用知识解决问题的能力。同时,在练习过程中及时反馈和指导,帮助学生查漏补缺。
问题引导法:在教学过程中,适时提出有思考价值的问题,引导学生主动思考、积极探索,培养学生的思维能力。如在讲解圆的基本元素时,提问学生生活中哪些现象可以用这些元素来解释。
四、教学过程
(一)导入新课(5 分钟)
运用多媒体展示生活中各种含有圆的精美图片,如车轮、摩天轮、圆形餐盘、奥运五环等,同时播放一些与圆相关的动态视频,如旋转的风扇、滚动的篮球等。
提问:同学们,在我们五彩斑斓的生活中,圆无处不在。大家仔细观察这些图片和视频,开动脑筋想一想,为什么车轮要做成圆形,而不是三角形、方形等其他形状呢?圆形的车轮在滚动过程中有什么独特的优势呢?
鼓励学生大胆发言,分享自己的想法,然后引导学生进行简单的讨论和交流,引发学生对圆的强烈好奇心和探究欲望,从而自然地引出本节课的课题 —— 圆的基本元素。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
问题一:你能在纸上画出一个圆吗?
借助圆规
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示,叫做圆O,记作⊙O
O
连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示.半径的长度就是圆规两个脚之间的距离.
r
通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示.
d
问题二:(1)根据借助圆规的画图过程,你知道什么是确定圆的要素吗?
一是圆心,圆心确定其位置;
二是半径,半径确定其大小.
(2)若有两个圆的半径相等,这两个圆有什么关系呢?
互为等圆;
(3)若有两个圆的半径相等,圆心的位置也相等,这两个圆有什么关系呢?
互为同圆;
问题三:在画图过程,圆上的点和圆心的距离有什么位置关系呢?
圆上各点到定点(圆心O)的距离都等于定长r;
到定点的距离等于定长的点都在同一个圆上;
圆的集合定义:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
A
O
r
问题一:在若随机在圆上任取两点A、B,连接AB,AB的长度有几种可能?
如图,线段AB过点O,则AB=d;
如图,线段AB'不过点O,则AB<d;
弦:连接圆上任意两点的线段叫做弦.
O
d
A
B'
B
注意:直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
探究一:圆的有关概念
圆上任意两点间的部分叫做圆弧,简称弧.
O
d
A
B'
B
问题5:你能用字母表示出图中的圆弧吗?
如图,以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
AB;
(
AB';
(
弦把圆分成两段圆弧,小于圆半周的叫做劣弧,如AB';
(
大于圆半周的叫做优弧,用ABB'表示;
(
探究二:圆心角
问题1:(1)你能在下图中找到几个角?
O
B
A
∠AOB;
∠ABO;
∠BAO;
(3)OA、OB、AB分别与圆有什么位置关系?
OA、OB分别是圆O的半径;
AB是圆O的弦;
(2)∠AOB在圆O上有什么位置特点?
∠AOB顶点在圆心,角的两边与圆相交
O
B
A
圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角,如∠AOB .
圆心角∠AOB所对的弦为AB.
圆心角∠AOB所对的弧为AB.
⌒
归纳总结
返回
1. “车轮为什么都做成圆形?”下面解释最合理的是( )
A.圆形是轴对称图形
B.圆形特别美观大方
C.圆形是曲线图形
D.从圆心到圆上任意一点的距离都相等
D
2.已知⊙O的半径是4 cm,则⊙O中最长的弦长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
C
返回
返回
120°
3.如图,A,B是⊙O上两个点,若∠OAB=30°,则∠AOB=________.
4.如图,在⊙O中,弦有________,直径是________,优弧有____________,劣弧有____________.
AC,AB
返回
AB
5.以定点O为圆心,定长a为半径,回答问题:
(1)这样的圆可以作________个;
(2)圆心可以确定圆的________;
(3)半径可以确定圆的________;
(4)圆将平面分为________部分,分别称为圆________,圆的________,圆的________.
返回
1
位置
大小
三
圆周
外部
内部
6.如图,圆O的周长为4π,B是弦CD上任意一点(与C,D不重合),过点B作OC的平行线交OD于点E,则EO+EB=________.
2
【点拨】∵⊙O的周长为4π,
∴⊙O的半径为2,即OD=2.
∵OC=OD,∴∠C=∠D.
∵BE∥OC,∴∠EBD=∠C,∴∠EBD=∠D.
∴BE=DE,∴EO+EB=EO+DE=OD=2.
返回
7.如图,点A,B,C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
【证明】连结OA,OC,AC,如图.
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO.
∵BO平分∠ABC,∴∠ABO=∠CBO.
∴∠BAO=∠BCO.
∵OA=OC,∴∠OAC=∠OCA.
∴∠BAO+∠OAC=∠BCO+∠OCA,
即∠BAC=∠BCA.∴AB=BC.
返回
8.[2024绥化期末]下列说法:
①弦是直径;
②半圆是弧;
③过圆心的线段是直径;
④圆心相同半径相同的两个圆是同心圆,
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
返回
C
9.如图,点A,D,G,M在半圆O上,四边形ABOC,四边形DEOF,四边形HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
A.a>b>c
B.c>a>b
C.a=b=c
D.b>c>a
【点拨】如图,连结OM,OD,OA.根据矩形的对角线相等,得BC=OA,EF=OD,NH=OM.再根据同圆的半径相等,得a=b=c.故选C.
【答案】 C
[变式]如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为________.
5
弦:连接圆上任意两点的线段叫做弦.
圆弧:圆上任意两点间的部分叫做圆弧,简称弧.
小于圆半周的叫做劣弧;
大于圆半周的叫做优弧;
圆心角:顶点在圆心,角的两边与圆相交的角叫圆心角.
谢谢观看!
