北师大八下5.4.3分式方程（3）

(共27张PPT)
第五章 分式与分式方程
5.4.3分式方程（3）
北师大版 数学 八年级 下册
学习目标
1. 会根据具体问题中的数量关系列出分式方程，体会分式方程是刻画现实世界数量关系的有效模型；
2. 会根据具体问题的实际意义检验方程解是否合理；
3. 会解决一些与分式方程有关的实际问题，发展分析问题，解决问题的能力和应用意识.
情景导入
1.解分式方程的基本思路是什么？
通过去分母将分式方程化为整式方程.
2.验根有哪几种方法？
有两种方法：第一种是代入最简公分母；第二种代入原分式方程.通常使用第一种方法.
情景导入
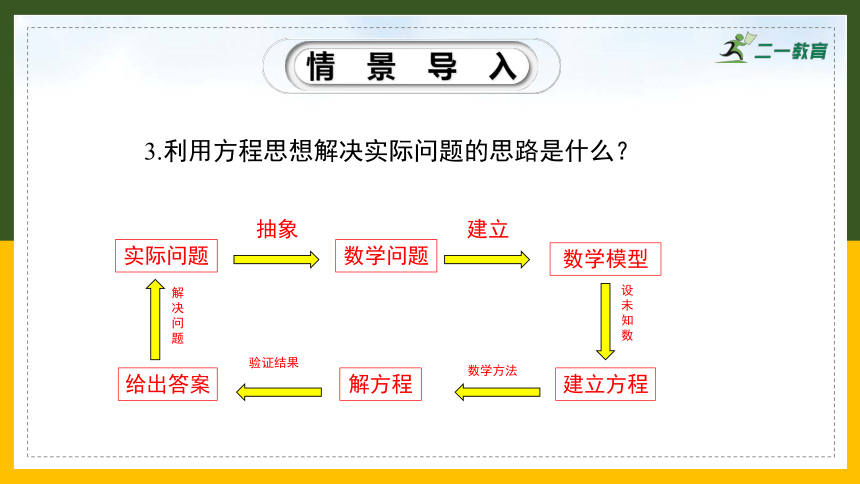
3.利用方程思想解决实际问题的思路是什么？
实际问题
数学问题
数学模型
建立方程
解方程
给出答案
抽象
建立
设未知数
数学方法
验证结果
解决问题
核心知识点一：
列分式方程解决营销问题
例1： 某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10. 2万元.
⑴你能找出这一情境中的等量关系吗
⑵根据这一情境你能提出哪些问题
探索新知
⑵根据这一情境你能提出哪些问题
⑴你能找出这一情境中的等量关系吗
等量关系:
①第二年每间房屋的租金- 第一年每间房屋的租金=500
②第一年出租的房屋数=第二年出租的房屋数
①每年有多少间房屋出租
②这两年每间房屋的租金各是多少
探索新知
解: ① 设每年有x 间房屋出租.
根据题意,得
解得 x=12
经检验: x=12 是原方程的解,也符合提意.
所以 每年有12间房屋出租
①每年有多少间房屋出租
探索新知
②这两年每间房屋的租金各是多少
解：由①得第一年每间房屋的租金为
﹙元﹚
第二年每间房屋的租金为
﹙元﹚
答:第一年每间房屋的租金为8000元，第二年每间房屋的租金为8500元.
探索新知
归纳总结
(1)检验是否是所列方程的解;
(2)检验是否满足实际意义.
有两次检验:
注意：
探索新知
①审：分析问题，寻找已知、未知及相等关系；
②设：设恰当的未知数；
③列：根据相等关系列出分式方程；
④解：求出所列方程的根；
⑤验：首先检验所求的根是不是分式方程的根，然后检验所求的根是否与实际相符；
⑥答：写出答语.
列分式方程解应用题时，可以按照以下的步骤：
归纳总结
探索新知
核心知识点二：
列分式方程解决商业问题
例2：某市从今年1月1日起调整居民用水价格,每吨水费上涨1/3,小丽家去年12月的水费是15元,今年7月的水费是30元.已知今年7月的用水量比去年12月的用水量多5m3,求该市今年居民用水的价格
探索新知
①今年用水价格=去年用水价格×
分析：此题的主要等量关系是：
②小丽家今年7月的用水量－小丽家去年12月的用水量=5m3.
③=
探索新知
解:设该市去年居民用水的价格为x元/m3,则今年居民用水的价格为x元/m3.
根据题意,得-=5,解得x=1.5.
经检验,x=1.5是所列方程的根.1.5×=2(元/m3).
所以,该市今年居民用水的价格为2元/m3.
探索新知
实际问题
找等量关系
设未知数、列方程
数学问题
(分式方程)
解方程
方程的解
检验
实际问题
的答案
建模
归纳总结
探索新知
当堂检测
1.某工厂现在平均每天比原计划多生产50台机器，现在生产400台机器所需时间比原计划生产450台机器所需时间少1天，设现在平均每天生产 台机器，则下列方程正确的是( ) .
A
A． B．
C． D．
当堂检测
2.某校八年级学生去距离学校 的游览区游览，一部分学生乘
慢车先行，出发 后，另一部分学生乘快车前往，结果他们同时到
达.已知快车的速度是慢车速度的1.5倍，求慢车的速度.设慢车的速度
是 ,所列方程正确的是( ) .
B
A． B．
C． D．
当堂检测
3.某校学生去距离学校 的博物馆参观，一部分学生骑自行车先
走，过了 后，其余学生乘汽车出发，结果他们同时到达.已知
汽车的速度是骑车学生速度的2倍，汽车的速度是( ) .
D
A． B．
C． D．
当堂检测
4.某市为解决冬季取暖问题需铺设一条长3 500米的管道，为尽量减少
施工对交通造成的影响，实际施工时“…”，设实际每天铺设管道 米，
则可得方程 ，根据此情景，题中用“…”表示的缺失的
条件应补为( ) .
A
A．每天比原计划多铺设10米，结果提前15天完成
B．每天比原计划少铺设10米，结果延期15天完成
C．每天比原计划少铺设15米，结果延期10天完成
D．每天比原计划多铺设15米，结果提前10天完成
当堂检测
5．“我市为处理污水，需要铺设一条长为4 000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设10米，结果提前20天完成任务．”根据题意可得方程－＝20，则方程中x表示( )．
A．实际每天铺设管道的长度
B．实际施工的天数
C．原计划每天铺设管道的长度
D．原计划施工的天数
A
当堂检测
6．某工厂计划加工一批零件240个，实际每天加工零件的个数是原计划的1.5倍，结果比原计划少用2天．设原计划每天加工零件x个，可列方程为 ．
- =2
7．商场先用3 200元购进一批防紫外线太阳伞，很快就销售一空．商场又用8 000元购进了第二批这种太阳伞，所购数量是第一批的2倍，但每把太阳伞贵了4元．则两次共购进这种太阳伞 把．
600
当堂检测
8.农历五月初五是中国民间传统端午节，某蛋糕店一直销售的是白水粽，端午节临近又推出了红豆粽，其中红豆粽的销售单价是白水粽的1.25倍，4月份，红豆粽和白水粽共销售150千克，红豆粽的销售额是1 200元，白水粽的销售额为1 440元.红豆粽、白水粽的销售单价各是多少？
当堂检测
解：设白水粽的销售单价为 元，则红豆粽的销售单价为 元，
依题意得 ，解得 ，
经检验， 是原方程的解，且符合题意，则
．
答：红豆粽的销售单价是20元，白水粽的销售单价是16元．
当堂检测
9.某地区制订对区、镇两级的旧城镇旧村居改造三年计划.现某村计划对面积为 的旧村居进行改造，安排 ， 两个公司完成.已知 公司每天能改造的面积是 公司的2倍，并且独立完成面积为 旧村居的改造时， 公司比 公司少用6天.
当堂检测
（1） ， 两公司每天能改造的面积分别是多少平方米？
解：设 公司每天能改造的面积为 ，则 公司每天能改造的
面积为 .
由题意得 ，解得 ，
经检验， 是原方程的解，且符合题意，
则 .
答： 公司每天能改造的面积为 ， 公司每天能改造的面积
为 .
当堂检测
（2）若每天需付给 公司的改造费用为0.8万元， 公司为0.3万元，
要使这次的改造总费用不超过60万元，至多应安排 公司工作多少天？
解：设应安排 公司工作 天，则安排 公司工作
天，
由题意得 ，
解得 .
答：至多应安排 公司工作30天．
列分式方程解应用题的步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.(1)检验是不是所列方程的解;
(2)检验是否满足实际意义.
6.答:注意单位和语言完整.
感谢收看