北师大八下5.1.1 认识分式（1）

(共25张PPT)
第五章 分式与分式方程
5.1.1 认识分式（1）
北师大版 数学 八年级 下册
学习目标
1．能根据分式的概念，辨别出分式，理解当分母为零时，分式无意义。
2．能确定分式中字母的取值范围，使分式有意义，或使分式的值为零。
3．会用分式表示实际问题中的数量关系。
情景导入
中国是世界上受荒漠化、沙化危害最严重的国家之一。全国荒漠化、沙化土地面积占国土面积约40%。
情景导入
核心知识点一：
分式的概念
面对日益严重的土地沙漠化问题，某县决定在一定期限内固沙造林2400hm2，实际每月固沙造林的面积比原计划多30hm2 ，结果提前完成原计划的任务.如果设原计划每月固沙造林xhm2，那么
（1）原计划完成造林任务需要多少月？
（2）实际完成造林任务用了多少个月？
探索新知
如果原计划每月固沙造林xhm2，那么
（1）原计划完成造林任务需要_____个月.
（2）实际完成造林任务用了______个月.
探索新知
2010年上海世博会吸引了成千上万的参观者，某一时段内的统计结果显示：
前 a 天平均每天参观人数 35 万人，则前a天参观人数共______万人
后 b 天平均每天参观人数 45 万人，则这（a + b）天参观人数共__________万人。
这（a + b）天平均每天参观人数是____ ___万人。
探索新知
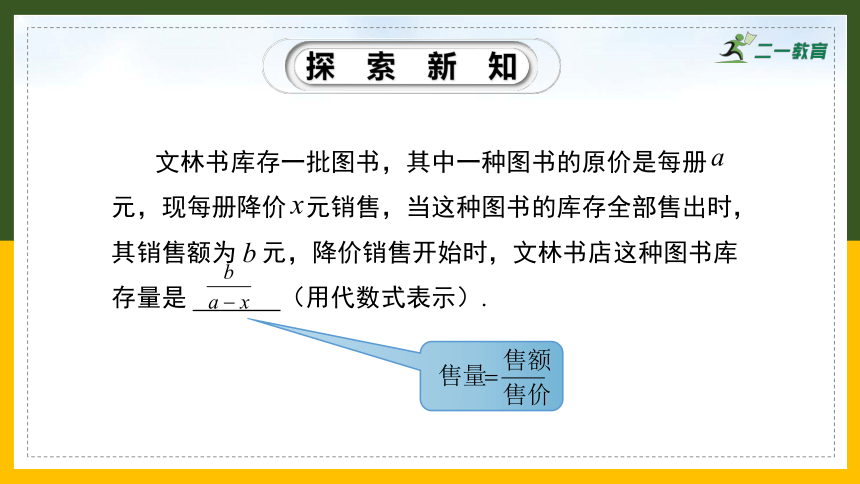
文林书库存一批图书，其中一种图书的原价是每册 元，现每册降价 元销售，当这种图书的库存全部售出时，其销售额为 元，降价销售开始时，文林书店这种图书库存量是 （用代数式表示）.
探索新知
它们有什么共同特征？它们与整式有什么不同？
（1）都有分子、分母与分数线构成；
（2）分子、分母都是整式；
（3）分母中都含有字母；
不同点：它们的分母中都含有字母，而整式的分母中不含字母.
探索新知
归纳总结
一般地，用A，B表示两个整式，A÷B可以表示成 的形式.如果B中含有字母，那么称 为分式，其中A称为分式的分子，B称为分式的分母.对于任意一个分式，分母都不能为零.
注意：
（1）分式也是代数式；
（2）分式是两个整式的商，它的形式是　（其中A，B都是整式并且还要求B是含有字母的整式）；
（3）A称为分式的分子，B为分式的分母.
探索新知
练一练：下列各式中，哪些是整式？哪些是分式？
（1）5x-7; （2） （3）3x2-1;
（4） （5） （6）
（7） （8）
整式：1；2；3；8；9
分式：4；5；6；7.
探索新知
核心知识点二：
分式有意义和值为零的条件
（1）当a取何值时，分式 有意义
解: 当分母的值为零时，分式没有意义，
除此以外，分式都有意义。
由分母2a-1 ≠ 0，得a ≠ ,
所以,当a ≠ 时，分式 都有意义.
分式中不能使分母值为零，否则分式无意义
探索新知
(2)当a取何值时，分式 的值为0
解: 当分子为0时，分式 的值为0时，
由分子a-1=0，得a =-1
所以,当a =-1 时，分式 的值为0.
当分子为零且分母不为零时，分式值为零
探索新知
归纳总结
1.分式无意义的条件
2.分式有意义的条件
3.分式的值等于零的条件
分母等于零
分母不等于零
(1)分子等于零
(2)分母不等于零
探索新知
1.若分式 无意义，则x=______.
2.若分式 有意义，则x应取何值？
3.若分式 =0，则x=___________.
4.若分式 =0，则x=___________.
3或-3
任意实数
3
-3
练一练：
探索新知
当堂检测
1.当 时，下列分式没有意义的是( ) .
A
A． B． C． D．
2.分式 有意义的条件是( ) .
A
A． B． C． D． 为任意实数
当堂检测
3.如果分式 的值为0，那么 的值为( ) .
B
A． B．1 C． 或1 D．1或0
4.下列各式中： ， ， ， ，分式的个数为( ) .
D
A．0 B．4 C．3 D．2
当堂检测
5.关于分式，有下列说法，其中不正确的是（ ）.
A.当x＝－1，m＝2时，分式有意义
B.当x＝3时，分式的值一定为0
C.当x＝1，m＝3时，分式没有意义
D.当x＝3且m≠3时，分式的值为0
B
当堂检测
6.若表示一个整数，则整数x可取值的个数是（ ）.　　　　　　　　　　　　　　　
A.2个　 B.3个　 C.4个　 D.8个
B
7．一辆汽车以60千米/时的速度行驶，从A城到B城需t小时，如果该车的速度每小时增加v千米，那么从A城到B城需要( )小时．
A. B. C. D.
B
当堂检测
8.要使分式有意义，x的取值应满足的条件是 ．
x≠－2
9．有一个分式：①当x≠1时，分式有意义；②当x＝－2时，分式的值为0.请写出同时满足以上两个条件的一个分式： ．
(答案不唯一)
当堂检测
10.已知分式 .
（1）当 为何值时，此分式有意义？
解：由题意得， ，解得 且 .
（2）当 为何值时，此分式的值等于0？
解：由题意得， ， ，解得 ，
所以当 时，此分式的值为零.
（3）当 时，分式的值是多少？
解：当 时，原式 ．
当堂检测
11．当x满足什么条件时，下列分式有意义？
（1）；
（2）；
（3）;
（4） .
解：(1)x＋1≠0，解得x≠－1.
解：(2)∵x2＋1≥1，∴x为任意实数．
解：(3)1－|x|≠0，解得x≠±1.
解：(4)(x＋2)(x－1)≠0，解得x≠－2且x≠1.
当堂检测
12．若分式的值为整数，x的值也为整数，求x的最小值．
解：∵分式的值为整数，x的值也为整数，
∴x－1＝±4或±2或±1，
∴x＝5或－3或3或－1或2或0，
∴x的最小值为－3.
一个概念
三个条件
分母不等于零
分式有意义的条件：
分母等于零
分式无意义的条件：
分子等于零
且分母不等于零
分式的值为零的条件：
分式的概念
①分子分母都是整式
②分母中含有字母
③分母不能为零。
感谢收看