北师大八下5.3.2 分式的加减法(2)
文档属性
| 名称 | 北师大八下5.3.2 分式的加减法(2) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 11:38:16 | ||
图片预览







文档简介
(共27张PPT)
第五章 分式与分式方程
5.3.2 分式的加减法(2)
北师大版 数学 八年级 下册
学习目标
1.会确定几个分式的最简公分母,并根据分式的基本性质进行通分;
2.会运用通分法则进行异分母分式的加减.
情景导入
1.分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不为零的整式,分式的值不变.
2.同分母分式的加减法法则:
同分母的分式相加减,分母不变,把分子相加减.
情景导入
3.计算:
解:
核心知识点一:
最简公分母
如何计算:
依据?
转化
根据分数的基本性质,异分母分数转化为同分母分数,这一过程称为通分.
通分:
探索新知
你认为 应该怎样计算?
想一想,异分母的分式应该如何加减?
分数的通分
分式的通分
类比
根据分式的基本性质,异分母分式转化为同分母分式,这一过程称为通分.
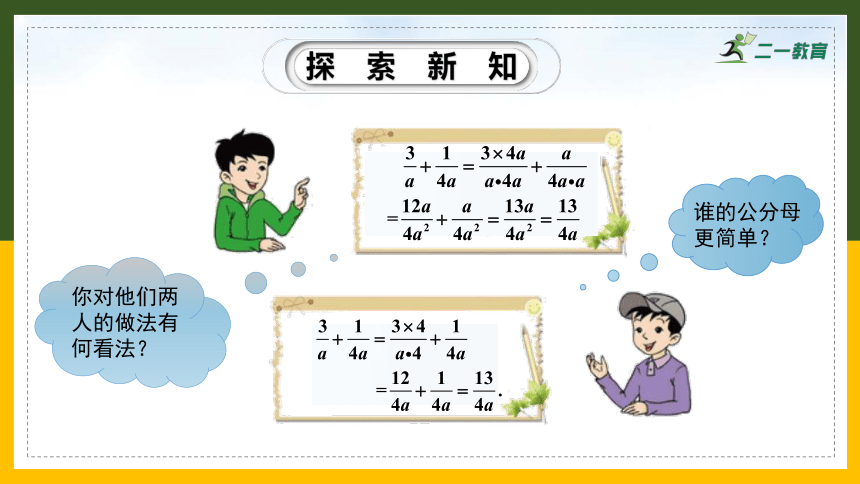
探索新知
你对他们两人的做法有何看法?
谁的公分母更简单?
探索新知
最简公分母:
观察并找出下面各组分式最简公分母:
思考:怎么找分式的最简公分母?
探索新知
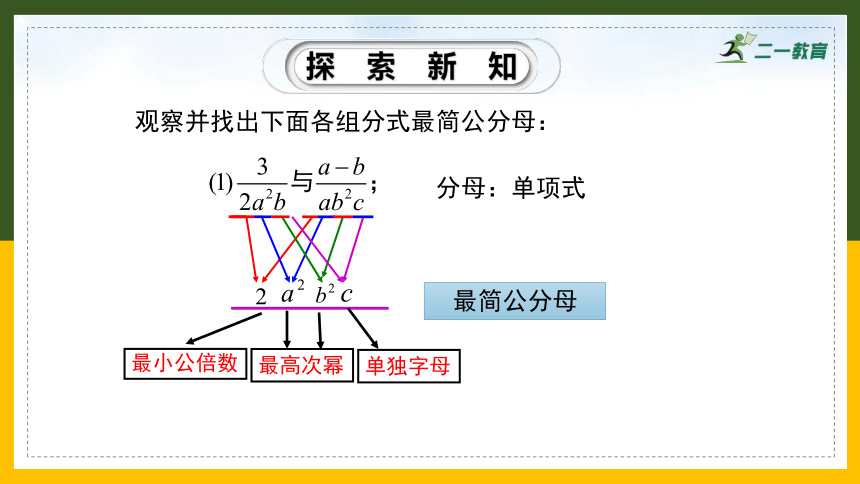
观察并找出下面各组分式最简公分母:
最小公倍数
最简公分母
最高次幂
单独字母
分母:单项式
探索新知
观察并找出下面各组分式最简公分母:
最简公分母(x-5)(x+5)
分母:多项式
x-5与x+5是不同的因式
探索新知
归纳总结
怎样确定最简公分母呢?
各分母系数的最小公倍数;
(3)定指数:
各分母中出现的所有字母或多项式都要取到;
分母中相同字母或多项式取最高次幂。
(2)定底数:
(1)定系数:
注意:分母中的多项式能因式分解的应先因式分解。
探索新知
解:
最简公分母是:
练一练:通分:
探索新知
练一练:通分:
解:
最简公分母是
(x-5)(x+5)
探索新知
核心知识点二:
异分母分式的加减
异分母分数的加减法法则:
异分母分数的加减法法则:
类比
探索新知
与异分母的分数加减法法则类似,异分母的分式加减法法则是:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
这一法则可以用式子表示:
用式子表示为:
归纳总结
探索新知
例:计算:
(1)
(2)
(3)
解(1)
(2)
(3)
探索新知
归纳总结
①通分:将异分母分式化成同分母分式;
②写成“分母不变,分子相加减”的形式;
③分子化简:分子去括号、合并同类项;
④约分:结果化为最简分式或整式.
异分母分式的加减运算步骤:
探索新知
当堂检测
A.(x+3y)(x-3y) B.2(x-3y)(x+3y)
C.3(x+3y)(x-3y) D.2(x-3y)2
B
当堂检测
2.下列等式中,正确的是( )
C
当堂检测
C.a2 D.a-2b
A
当堂检测
C
当堂检测
5.计算.
当堂检测
解:方法一:
=2(x-1)-(x+1)
=x-3.
当堂检测
方法二:
=x-3.
当堂检测
1.异分母分式的加减法法则:
2.最简公分母的确定方法:
(3)因式的指数:相同因式取指数最高的.
(1)系数:取分母中各系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都要取到;
感谢收看
第五章 分式与分式方程
5.3.2 分式的加减法(2)
北师大版 数学 八年级 下册
学习目标
1.会确定几个分式的最简公分母,并根据分式的基本性质进行通分;
2.会运用通分法则进行异分母分式的加减.
情景导入
1.分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不为零的整式,分式的值不变.
2.同分母分式的加减法法则:
同分母的分式相加减,分母不变,把分子相加减.
情景导入
3.计算:
解:
核心知识点一:
最简公分母
如何计算:
依据?
转化
根据分数的基本性质,异分母分数转化为同分母分数,这一过程称为通分.
通分:
探索新知
你认为 应该怎样计算?
想一想,异分母的分式应该如何加减?
分数的通分
分式的通分
类比
根据分式的基本性质,异分母分式转化为同分母分式,这一过程称为通分.
探索新知
你对他们两人的做法有何看法?
谁的公分母更简单?
探索新知
最简公分母:
观察并找出下面各组分式最简公分母:
思考:怎么找分式的最简公分母?
探索新知
观察并找出下面各组分式最简公分母:
最小公倍数
最简公分母
最高次幂
单独字母
分母:单项式
探索新知
观察并找出下面各组分式最简公分母:
最简公分母(x-5)(x+5)
分母:多项式
x-5与x+5是不同的因式
探索新知
归纳总结
怎样确定最简公分母呢?
各分母系数的最小公倍数;
(3)定指数:
各分母中出现的所有字母或多项式都要取到;
分母中相同字母或多项式取最高次幂。
(2)定底数:
(1)定系数:
注意:分母中的多项式能因式分解的应先因式分解。
探索新知
解:
最简公分母是:
练一练:通分:
探索新知
练一练:通分:
解:
最简公分母是
(x-5)(x+5)
探索新知
核心知识点二:
异分母分式的加减
异分母分数的加减法法则:
异分母分数的加减法法则:
类比
探索新知
与异分母的分数加减法法则类似,异分母的分式加减法法则是:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
这一法则可以用式子表示:
用式子表示为:
归纳总结
探索新知
例:计算:
(1)
(2)
(3)
解(1)
(2)
(3)
探索新知
归纳总结
①通分:将异分母分式化成同分母分式;
②写成“分母不变,分子相加减”的形式;
③分子化简:分子去括号、合并同类项;
④约分:结果化为最简分式或整式.
异分母分式的加减运算步骤:
探索新知
当堂检测
A.(x+3y)(x-3y) B.2(x-3y)(x+3y)
C.3(x+3y)(x-3y) D.2(x-3y)2
B
当堂检测
2.下列等式中,正确的是( )
C
当堂检测
C.a2 D.a-2b
A
当堂检测
C
当堂检测
5.计算.
当堂检测
解:方法一:
=2(x-1)-(x+1)
=x-3.
当堂检测
方法二:
=x-3.
当堂检测
1.异分母分式的加减法法则:
2.最简公分母的确定方法:
(3)因式的指数:相同因式取指数最高的.
(1)系数:取分母中各系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都要取到;
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
