27.2.2 直线与圆的位置关系 课件(共28张PPT)
文档属性
| 名称 | 27.2.2 直线与圆的位置关系 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
27.2.2 直线与圆的位置关系
第27章 圆
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解直线与圆有相交、相切、相离三种位置关系
2.能根据圆心到直线的距离d和圆的半径r之间的数量关系,判断出直线与圆的位置关系
教学重点
圆的定义及圆的基本元素的概念,尤其是帮助学生区分相似概念,如弦与直径、优弧与劣弧等。
同圆或等圆中半径相等这一性质的理解和应用,通过多样化的例题让学生熟练掌握该性质在不同情境下的运用。
教学难点
对圆的集合定义的深入理解,通过具体的点的位置判断、动态演示等方式,让学生真正领会平面内到定点的距离等于定长的所有点组成的图形叫做圆。
灵活运用圆的基本元素的性质解决综合性相关问题,通过逐步引导和练习,提升学生分析问题和解决问题的能力。
三、教学方法
讲授法:以清晰、准确且生动的语言,向学生系统讲解圆的定义、基本元素的概念及相关性质,确保学生扎实掌握基础知识。在讲解过程中,注重概念的引入和解释,让学生理解知识的来龙去脉。
直观演示法:充分利用多媒体课件、圆规、直尺等工具,通过动态演示、实物操作等方式,直观展示圆的形成过程、各基本元素的特征,帮助学生建立直观且深刻的认识。例如用动画展示圆的集合定义的形成过程。
小组合作探究法:精心组织学生进行小组讨论和合作探究活动,设置有启发性的问题,让学生在交流互动中深化对圆的基本元素的理解,培养学生的合作能力和探究精神。如让小组探究同圆中不同弦长与圆心距离的关系。
练习巩固法:设计针对性强、层次分明的练习题,从基础到提高再到拓展,让学生及时巩固所学知识,逐步提高学生运用知识解决问题的能力。同时,在练习过程中及时反馈和指导,帮助学生查漏补缺。
问题引导法:在教学过程中,适时提出有思考价值的问题,引导学生主动思考、积极探索,培养学生的思维能力。如在讲解圆的基本元素时,提问学生生活中哪些现象可以用这些元素来解释。
四、教学过程
(一)导入新课(5 分钟)
运用多媒体展示生活中各种含有圆的精美图片,如车轮、摩天轮、圆形餐盘、奥运五环等,同时播放一些与圆相关的动态视频,如旋转的风扇、滚动的篮球等。
提问:同学们,在我们五彩斑斓的生活中,圆无处不在。大家仔细观察这些图片和视频,开动脑筋想一想,为什么车轮要做成圆形,而不是三角形、方形等其他形状呢?圆形的车轮在滚动过程中有什么独特的优势呢?
鼓励学生大胆发言,分享自己的想法,然后引导学生进行简单的讨论和交流,引发学生对圆的强烈好奇心和探究欲望,从而自然地引出本节课的课题 —— 圆的基本元素。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
看一看:观察下面几幅图形,试着发现它们的规律.
太阳升起一半
太阳刚升起,与水平线相交
太阳完全升起
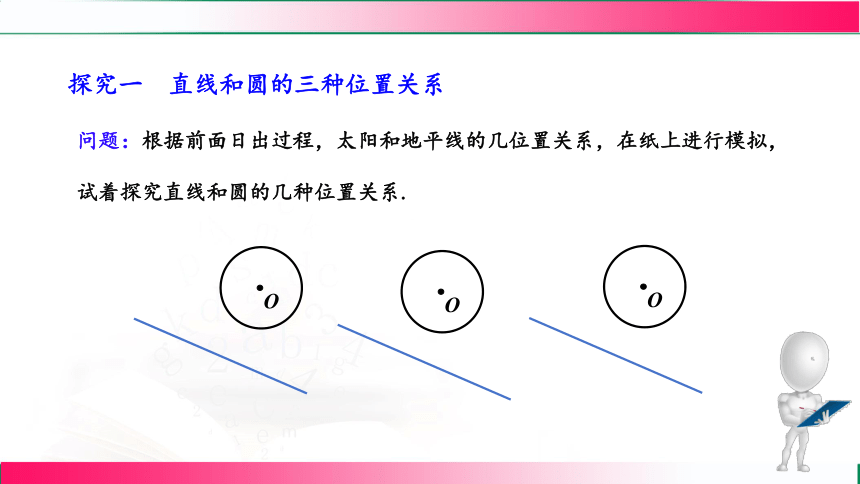
探究一 直线和圆的三种位置关系
问题:根据前面日出过程,太阳和地平线的几位置关系,在纸上进行模拟,
试着探究直线和圆的几种位置关系.
O
O
O
O
直线和圆有两个公共点
定义:直线和圆有两个公共点,这时直线与圆的位置关系叫做相交,这条直线叫做圆的割线.
O
直线和圆有一个公共点
定义:直线和圆有一个公共点,这时直线与圆的位置关系叫做相切,这条直线叫做圆的切线,这个公共点叫做切点.
O
直线和圆没有公共点
定义:直线和圆没有公共点,这时直线与圆的位置关系叫做相离.
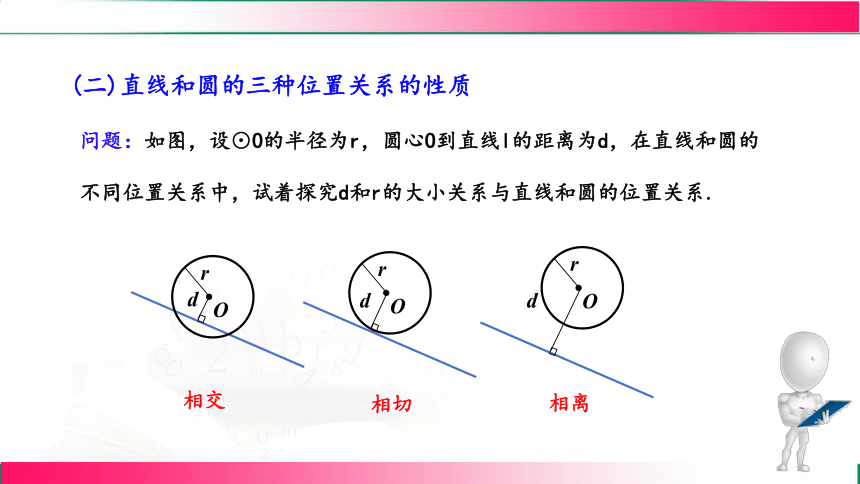
(二)直线和圆的三种位置关系的性质
问题:如图,设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的
不同位置关系中,试着探究d和r的大小关系与直线和圆的位置关系.
相切
相交
相离
O
d
r
O
d
r
O
d
r
归纳总结
直线和圆的三种位置关系的性质:
根据直线和圆相交、相切、相离的定义,容易得到:
直线和圆相交 .
直线和圆相切 .
直线和圆相离 .
d<r
d=r
d>r
O
d
r
O
d
r
O
d
r
例1.如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1)以点C为圆心,当半径为多少时,AB与☉C相切?
A
C
B
D
解: 过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
∴∠B=60°,
(2)以点C为圆心、半径 r 分别为 4cm 和 5cm 作两个圆,
这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
D
当r =4cm时,d>r,⊙C与AB相离;
解:由 (1) 可知圆心 C 到 AB 的距离为 .
当r =5cm时,d<r,⊙C与AB相交.
归纳总结
判断直线与圆的位置关系有两种方法:
(1)从交点的个数识别直线与圆的位置关系;
(2)先求出圆心到直线的距离,然后比较这个距离与圆的半径的大小,
最后得出结论.
返回
1.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
B
2.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
A
返回
返回
D
3.[2024周口期末]已知⊙O的半径是一元二次方程x2-7x+12=0的一个根,圆心O到直线l的距离d=3,则直线l与⊙O的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
4.已知∠AOB=30°,M为OB上一点,且OM=5 cm,若以M为圆心,r为半径作圆,那么:(1)当直线OA与⊙M相离时,r的取值范围是________;(2)当r=________时,直线OA与⊙M相切;(3)当直线OA与⊙M有公共点时,r的取值范围是________.
返回
5. [教材P50练习T1] 如图所示,在Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,以C为圆心,r为半径的圆与直线AB有何位置关系?为什么?
(1)r=4 cm.
返回
(2)r=4.8 cm.
(3)r=6 cm.
【解】当r=4.8 cm时,h=r,则AB与⊙C相切.
当r=6 cm时,r>h,则AB与⊙C相交.
返回
6.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
D
【答案】 C
1.直线与圆的位置关系的概念
如果直线与圆有两个公共点,这时直线与圆的位置关系叫做________,
这条直线叫做圆的________;
如果直线与圆只有一个公共点,这时直线与圆的位置关系叫做________,
这条直线叫做圆的________,这个公共点叫做________;
如果直线与圆没有公共点,这时直线与圆的位置关系叫做________.
相交
相切
相离
切点
割线
切线
2.直线和圆的位置关系与d(圆心到直线的距离)和r(圆半径)的关系
直线与圆的位置关系 相交 相切 相离
公共点个数 2 1 0
d与r的关系
dd=r
d>r
谢谢观看!
27.2.2 直线与圆的位置关系
第27章 圆
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解直线与圆有相交、相切、相离三种位置关系
2.能根据圆心到直线的距离d和圆的半径r之间的数量关系,判断出直线与圆的位置关系
教学重点
圆的定义及圆的基本元素的概念,尤其是帮助学生区分相似概念,如弦与直径、优弧与劣弧等。
同圆或等圆中半径相等这一性质的理解和应用,通过多样化的例题让学生熟练掌握该性质在不同情境下的运用。
教学难点
对圆的集合定义的深入理解,通过具体的点的位置判断、动态演示等方式,让学生真正领会平面内到定点的距离等于定长的所有点组成的图形叫做圆。
灵活运用圆的基本元素的性质解决综合性相关问题,通过逐步引导和练习,提升学生分析问题和解决问题的能力。
三、教学方法
讲授法:以清晰、准确且生动的语言,向学生系统讲解圆的定义、基本元素的概念及相关性质,确保学生扎实掌握基础知识。在讲解过程中,注重概念的引入和解释,让学生理解知识的来龙去脉。
直观演示法:充分利用多媒体课件、圆规、直尺等工具,通过动态演示、实物操作等方式,直观展示圆的形成过程、各基本元素的特征,帮助学生建立直观且深刻的认识。例如用动画展示圆的集合定义的形成过程。
小组合作探究法:精心组织学生进行小组讨论和合作探究活动,设置有启发性的问题,让学生在交流互动中深化对圆的基本元素的理解,培养学生的合作能力和探究精神。如让小组探究同圆中不同弦长与圆心距离的关系。
练习巩固法:设计针对性强、层次分明的练习题,从基础到提高再到拓展,让学生及时巩固所学知识,逐步提高学生运用知识解决问题的能力。同时,在练习过程中及时反馈和指导,帮助学生查漏补缺。
问题引导法:在教学过程中,适时提出有思考价值的问题,引导学生主动思考、积极探索,培养学生的思维能力。如在讲解圆的基本元素时,提问学生生活中哪些现象可以用这些元素来解释。
四、教学过程
(一)导入新课(5 分钟)
运用多媒体展示生活中各种含有圆的精美图片,如车轮、摩天轮、圆形餐盘、奥运五环等,同时播放一些与圆相关的动态视频,如旋转的风扇、滚动的篮球等。
提问:同学们,在我们五彩斑斓的生活中,圆无处不在。大家仔细观察这些图片和视频,开动脑筋想一想,为什么车轮要做成圆形,而不是三角形、方形等其他形状呢?圆形的车轮在滚动过程中有什么独特的优势呢?
鼓励学生大胆发言,分享自己的想法,然后引导学生进行简单的讨论和交流,引发学生对圆的强烈好奇心和探究欲望,从而自然地引出本节课的课题 —— 圆的基本元素。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
看一看:观察下面几幅图形,试着发现它们的规律.
太阳升起一半
太阳刚升起,与水平线相交
太阳完全升起
探究一 直线和圆的三种位置关系
问题:根据前面日出过程,太阳和地平线的几位置关系,在纸上进行模拟,
试着探究直线和圆的几种位置关系.
O
O
O
O
直线和圆有两个公共点
定义:直线和圆有两个公共点,这时直线与圆的位置关系叫做相交,这条直线叫做圆的割线.
O
直线和圆有一个公共点
定义:直线和圆有一个公共点,这时直线与圆的位置关系叫做相切,这条直线叫做圆的切线,这个公共点叫做切点.
O
直线和圆没有公共点
定义:直线和圆没有公共点,这时直线与圆的位置关系叫做相离.
(二)直线和圆的三种位置关系的性质
问题:如图,设⊙O的半径为r,圆心O到直线l的距离为d,在直线和圆的
不同位置关系中,试着探究d和r的大小关系与直线和圆的位置关系.
相切
相交
相离
O
d
r
O
d
r
O
d
r
归纳总结
直线和圆的三种位置关系的性质:
根据直线和圆相交、相切、相离的定义,容易得到:
直线和圆相交 .
直线和圆相切 .
直线和圆相离 .
d<r
d=r
d>r
O
d
r
O
d
r
O
d
r
例1.如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1)以点C为圆心,当半径为多少时,AB与☉C相切?
A
C
B
D
解: 过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
∴∠B=60°,
(2)以点C为圆心、半径 r 分别为 4cm 和 5cm 作两个圆,
这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
D
当r =4cm时,d>r,⊙C与AB相离;
解:由 (1) 可知圆心 C 到 AB 的距离为 .
当r =5cm时,d<r,⊙C与AB相交.
归纳总结
判断直线与圆的位置关系有两种方法:
(1)从交点的个数识别直线与圆的位置关系;
(2)先求出圆心到直线的距离,然后比较这个距离与圆的半径的大小,
最后得出结论.
返回
1.已知⊙O的半径为5,圆心O到直线l的距离为3,则反映直线l与⊙O的位置关系的图形是( )
B
2.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆( )
A.与x轴相离,与y轴相切
B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交
D.与x轴相切,与y轴相离
A
返回
返回
D
3.[2024周口期末]已知⊙O的半径是一元二次方程x2-7x+12=0的一个根,圆心O到直线l的距离d=3,则直线l与⊙O的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
4.已知∠AOB=30°,M为OB上一点,且OM=5 cm,若以M为圆心,r为半径作圆,那么:(1)当直线OA与⊙M相离时,r的取值范围是________;(2)当r=________时,直线OA与⊙M相切;(3)当直线OA与⊙M有公共点时,r的取值范围是________.
返回
5. [教材P50练习T1] 如图所示,在Rt△ABC中,∠C=90°,AC=6 cm,BC=8 cm,以C为圆心,r为半径的圆与直线AB有何位置关系?为什么?
(1)r=4 cm.
返回
(2)r=4.8 cm.
(3)r=6 cm.
【解】当r=4.8 cm时,h=r,则AB与⊙C相切.
当r=6 cm时,r>h,则AB与⊙C相交.
返回
6.如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
D
【答案】 C
1.直线与圆的位置关系的概念
如果直线与圆有两个公共点,这时直线与圆的位置关系叫做________,
这条直线叫做圆的________;
如果直线与圆只有一个公共点,这时直线与圆的位置关系叫做________,
这条直线叫做圆的________,这个公共点叫做________;
如果直线与圆没有公共点,这时直线与圆的位置关系叫做________.
相交
相切
相离
切点
割线
切线
2.直线和圆的位置关系与d(圆心到直线的距离)和r(圆半径)的关系
直线与圆的位置关系 相交 相切 相离
公共点个数 2 1 0
d与r的关系
d
d>r
谢谢观看!
