28.2 用样本估计总体 课件(共25张PPT)
文档属性
| 名称 | 28.2 用样本估计总体 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 21:24:02 | ||
图片预览








文档简介
(共25张PPT)
28.2 用样本估计总体
第28章 样本与总体
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解简单随机抽样的意义,会进行简单随机抽样并用样本估计总体.(重点)
2.能够运用简单随机抽样分析实际问题.
练习过程中,让学生独立完成,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
总体、个体、样本、样本容量的概念。请学生用自己的语言表述这些概念,并举例说明。
抽样调查的必要性及常见的抽样方法,如简单随机抽样和分层抽样的特点和应用。
用样本统计量估计总体特征的方法和注意事项。
强调重点和易错点,鼓励学生在课后多观察生活中的统计现象,运用所学知识进行分析。
(六)布置作业(5 分钟)
基础作业
为了解某班学生的数学成绩情况,从该班 50 名学生中抽取 10 名学生的数学成绩进行分析。指出这个问题中的总体、个体、样本和样本容量。
某果园有苹果树 1000 棵,为了解这些苹果树的产量情况,从中抽取了 50 棵苹果树的产量进行统计分析。若这 50 棵苹果树的平均产量为 80 千克,估计该果园苹果的总产量。
某学校有教师 150 人,其中高级教师 30 人,中级教师 90 人,初级教师 30 人。现采用分层抽样的方法抽取一个容量为 30 的样本,求从高级、中级、初级教师中分别抽取的人数。
拓展作业
设计一个调查方案,了解你所在社区居民对垃圾分类的知晓率和参与度。要求明确总体、个体、样本、样本容量及抽样方法。
实践作业
选择一个自己感兴趣的统计问题,如调查同学们喜欢的音乐类型、手机品牌等,进行数据收集和分析,并撰写一份简单的统计报告。
五、教学反思
在本节课的教学中,通过丰富的生活实例引导学生理解样本与总体的相关概念,学生对知识的接受度较好。小组合作探究和实践操作活动让学生积极参与到课堂中,提高了学生的动手能力和合作能力。但在教学过程中,对于抽样方法的实际应用,部分学生可能理解不够深入,在今后的教学中,可以增加更多实际案例的分析和讨论,让学生更好地掌握抽样方法的选择和应用。同时,要进一步加强对学生实践活动的指导,提高学生数据收集和分析的准确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
(一)简单的随机抽样
要使样本具有代表性,不偏向总体中的某些个体,有一个对每个个体都公平的办法,那就是用抽签的办法决定哪些个体进入样本.统计学家们称这种理想的抽样方法为简单随机抽样.
(二)简单的随机抽样的方法
(1)先将每个个体编号;
(2)然后将写有这些编号的纸条全部放入一个盒子,搅拌均匀;
(3)再用抽签的办法,抽出一个编号,那个编号的个体就被选入样本.
抽样之前,我们不能预测到哪些个体会被抽中,像这样不能够事先预测结果的特性叫做随机性.
探究一 简单随机抽样
1.某校生物兴趣小组的同学们想探求人的各种血型(A、B、AB、O型四种)在人群中的比例,于是他们就在医院中心血库采血室门前调查了从上午8:00到9:00这一小时内参加献血的人员.
问题1:本问题中的总体、样本分别是什么?
总体是人的各种血型,样本是一小时内参加献血的人员的血型
问题2:他们的抽样是简单的随机抽样吗?
他们的抽样不是简单的随机抽样,因为他们的做法不符合随机抽样的规则
问题3:你想出了什么样的调查方案?
如在大街上随机询问经过此地的人员的血型等方法,只要抽样的样本是具有随机性即可.
归纳总结:
抽样是否是随机抽样取决于该抽样是否符合随机抽样的规则,是否具有随机性,只有对每一个个体都公平的抽样,才是随机抽样.
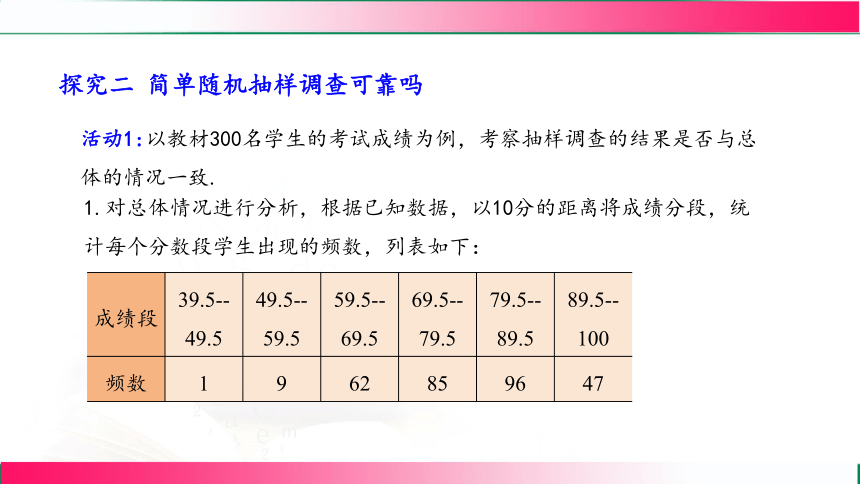
探究二 简单随机抽样调查可靠吗
活动1:以教材300名学生的考试成绩为例,考察抽样调查的结果是否与总体的情况一致.
1.对总体情况进行分析,根据已知数据,以10分的距离将成绩分段,统计每个分数段学生出现的频数,列表如下:
成绩段 39.5--49.5 49.5--59.5 59.5--69.5 69.5--79.5 79.5--89.5 89.5--100
频数 1 9 62 85 96 47
2.根据上表绘制直方图,如下:
0
20
40
60
80
100
120
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
这个分数段的学生最多
这个分数段的学生较少
总体的平均数为:78.1
方差为:116.3
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本一
平均数为:78
方差为:100.4
3.下面是小王同学绘制的三个样本频数分布直方图,并计算出了平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二
平均数为:74.2
方差为:14.56
样本三
平均数为:80.8
方差为:42.16
问题1:三张图与总体频数分布直方图相像吗?样本的平均数与总体的接近吗?
不同样本的平均数与方差差异较大,可能是因为样本太小.
问题2:再增加样本的容量,样本的平均数和方差趋势如何
随着样本容量的增加,样本的平均数和方差有接近于总体的平均数和方差的趋势.
活动2:为了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:根据抽样调查结果,估计该区12000名初中学生视力不低于4.8的人数是多少?
学生视力不低于4.8的人数有7200名.
解:
归纳总结:
由简单随机抽样获得样本容量较大的样本,可以用样本平均数、样本方差估计总体平均数和总体方差.
返回
1.为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是( )
A.企业男员工
B.企业年满50岁及以上的员工
C.用企业人员名册,随机抽取三分之一员工
D.企业新进员工
C
2.为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,小明计划进行抽样调查,你认为以下方案中最合理的是( )
A.抽取甲校七年级学生进行调查
B.在四所学校随机抽取200名学生进行调查
C.在乙校中随机抽取200名学生进行调查
D.在四所学校各随机抽取200名学生进行调查
D
返回
返回
3.要了解某校初中学生的课外作业负担情况,若采用抽样调查的方法进行调查,则下面哪种调查方式具有代表性( )
A.调查全体女生
B.调查全体男生
C.调查七、八、九年级各100名学生
D.调查九年级全体学生
C
4.[2024合肥期末]某课外兴趣小组为了解所在地区老年人的健康状况,分别作了四种不同的抽样调查.你认为抽样比较合理的是( )
A.在公园调查了800名老年人的健康状况
B.在医院调查了800名老年人的健康状况
C.调查了20名老年邻居的健康状况
D.利用派出所的户籍网随机调查了该地区15%的老年人的健康状况
D
返回
5.某冰箱生产厂家对某地区两个经销本厂冰箱的大型商场进行调查,调查结果显示:该厂冰箱的销售量占这两个商场同类产品销售量的45%,于是,该厂在广告中宣传,他们的产品销售量在国内同类产品销售量中占45%.小明根据自己所学的统计知识,判断这个宣传数据不可靠,他的依据是_________________________
__________.
返回
所取的样本容量太小,样本
缺乏代表性
6.小龙的妈妈让小龙去买一盒火柴,并叮嘱小龙,一定要试试火柴是否好用.小龙回家后,高兴地告诉妈妈:“火柴好用,我每根都试过了.”
(1)小龙采取的是哪种调查?
【解】小龙采取的是普查.
返回
(2)你认为小龙采取的方法是否合适?请说明理由.
【解】小龙采取的方法不合适,因为具有破坏性,所以应用抽样调查.
7.某食品加工厂有5条生产线,每条生产线一天能出产品20箱.质检员将对某日产品进行抽检,下列抽检方案中,最适宜的是( )
A.在该日的100箱产品中随机抽取1箱
B.抽取该日每条生产线的最后1箱产品
C.在该日每条生产线的产品中随机抽取1箱
D.抽取该日其中一条生产线的20箱产品
C
返回
样本估计总体
简单随机抽样
样本估计总体
1.样本具有代表性
2.用抽签的办法决定哪些个体进入样本
样本容量较大,可以用样本估计总体.
谢谢观看!
28.2 用样本估计总体
第28章 样本与总体
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.理解简单随机抽样的意义,会进行简单随机抽样并用样本估计总体.(重点)
2.能够运用简单随机抽样分析实际问题.
练习过程中,让学生独立完成,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
总体、个体、样本、样本容量的概念。请学生用自己的语言表述这些概念,并举例说明。
抽样调查的必要性及常见的抽样方法,如简单随机抽样和分层抽样的特点和应用。
用样本统计量估计总体特征的方法和注意事项。
强调重点和易错点,鼓励学生在课后多观察生活中的统计现象,运用所学知识进行分析。
(六)布置作业(5 分钟)
基础作业
为了解某班学生的数学成绩情况,从该班 50 名学生中抽取 10 名学生的数学成绩进行分析。指出这个问题中的总体、个体、样本和样本容量。
某果园有苹果树 1000 棵,为了解这些苹果树的产量情况,从中抽取了 50 棵苹果树的产量进行统计分析。若这 50 棵苹果树的平均产量为 80 千克,估计该果园苹果的总产量。
某学校有教师 150 人,其中高级教师 30 人,中级教师 90 人,初级教师 30 人。现采用分层抽样的方法抽取一个容量为 30 的样本,求从高级、中级、初级教师中分别抽取的人数。
拓展作业
设计一个调查方案,了解你所在社区居民对垃圾分类的知晓率和参与度。要求明确总体、个体、样本、样本容量及抽样方法。
实践作业
选择一个自己感兴趣的统计问题,如调查同学们喜欢的音乐类型、手机品牌等,进行数据收集和分析,并撰写一份简单的统计报告。
五、教学反思
在本节课的教学中,通过丰富的生活实例引导学生理解样本与总体的相关概念,学生对知识的接受度较好。小组合作探究和实践操作活动让学生积极参与到课堂中,提高了学生的动手能力和合作能力。但在教学过程中,对于抽样方法的实际应用,部分学生可能理解不够深入,在今后的教学中,可以增加更多实际案例的分析和讨论,让学生更好地掌握抽样方法的选择和应用。同时,要进一步加强对学生实践活动的指导,提高学生数据收集和分析的准确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
(一)简单的随机抽样
要使样本具有代表性,不偏向总体中的某些个体,有一个对每个个体都公平的办法,那就是用抽签的办法决定哪些个体进入样本.统计学家们称这种理想的抽样方法为简单随机抽样.
(二)简单的随机抽样的方法
(1)先将每个个体编号;
(2)然后将写有这些编号的纸条全部放入一个盒子,搅拌均匀;
(3)再用抽签的办法,抽出一个编号,那个编号的个体就被选入样本.
抽样之前,我们不能预测到哪些个体会被抽中,像这样不能够事先预测结果的特性叫做随机性.
探究一 简单随机抽样
1.某校生物兴趣小组的同学们想探求人的各种血型(A、B、AB、O型四种)在人群中的比例,于是他们就在医院中心血库采血室门前调查了从上午8:00到9:00这一小时内参加献血的人员.
问题1:本问题中的总体、样本分别是什么?
总体是人的各种血型,样本是一小时内参加献血的人员的血型
问题2:他们的抽样是简单的随机抽样吗?
他们的抽样不是简单的随机抽样,因为他们的做法不符合随机抽样的规则
问题3:你想出了什么样的调查方案?
如在大街上随机询问经过此地的人员的血型等方法,只要抽样的样本是具有随机性即可.
归纳总结:
抽样是否是随机抽样取决于该抽样是否符合随机抽样的规则,是否具有随机性,只有对每一个个体都公平的抽样,才是随机抽样.
探究二 简单随机抽样调查可靠吗
活动1:以教材300名学生的考试成绩为例,考察抽样调查的结果是否与总体的情况一致.
1.对总体情况进行分析,根据已知数据,以10分的距离将成绩分段,统计每个分数段学生出现的频数,列表如下:
成绩段 39.5--49.5 49.5--59.5 59.5--69.5 69.5--79.5 79.5--89.5 89.5--100
频数 1 9 62 85 96 47
2.根据上表绘制直方图,如下:
0
20
40
60
80
100
120
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
这个分数段的学生最多
这个分数段的学生较少
总体的平均数为:78.1
方差为:116.3
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本一
平均数为:78
方差为:100.4
3.下面是小王同学绘制的三个样本频数分布直方图,并计算出了平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二
平均数为:74.2
方差为:14.56
样本三
平均数为:80.8
方差为:42.16
问题1:三张图与总体频数分布直方图相像吗?样本的平均数与总体的接近吗?
不同样本的平均数与方差差异较大,可能是因为样本太小.
问题2:再增加样本的容量,样本的平均数和方差趋势如何
随着样本容量的增加,样本的平均数和方差有接近于总体的平均数和方差的趋势.
活动2:为了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:根据抽样调查结果,估计该区12000名初中学生视力不低于4.8的人数是多少?
学生视力不低于4.8的人数有7200名.
解:
归纳总结:
由简单随机抽样获得样本容量较大的样本,可以用样本平均数、样本方差估计总体平均数和总体方差.
返回
1.为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是( )
A.企业男员工
B.企业年满50岁及以上的员工
C.用企业人员名册,随机抽取三分之一员工
D.企业新进员工
C
2.为了解甲、乙、丙、丁四所学校学生对“122交通安全专题”相关知识的掌握情况,小明计划进行抽样调查,你认为以下方案中最合理的是( )
A.抽取甲校七年级学生进行调查
B.在四所学校随机抽取200名学生进行调查
C.在乙校中随机抽取200名学生进行调查
D.在四所学校各随机抽取200名学生进行调查
D
返回
返回
3.要了解某校初中学生的课外作业负担情况,若采用抽样调查的方法进行调查,则下面哪种调查方式具有代表性( )
A.调查全体女生
B.调查全体男生
C.调查七、八、九年级各100名学生
D.调查九年级全体学生
C
4.[2024合肥期末]某课外兴趣小组为了解所在地区老年人的健康状况,分别作了四种不同的抽样调查.你认为抽样比较合理的是( )
A.在公园调查了800名老年人的健康状况
B.在医院调查了800名老年人的健康状况
C.调查了20名老年邻居的健康状况
D.利用派出所的户籍网随机调查了该地区15%的老年人的健康状况
D
返回
5.某冰箱生产厂家对某地区两个经销本厂冰箱的大型商场进行调查,调查结果显示:该厂冰箱的销售量占这两个商场同类产品销售量的45%,于是,该厂在广告中宣传,他们的产品销售量在国内同类产品销售量中占45%.小明根据自己所学的统计知识,判断这个宣传数据不可靠,他的依据是_________________________
__________.
返回
所取的样本容量太小,样本
缺乏代表性
6.小龙的妈妈让小龙去买一盒火柴,并叮嘱小龙,一定要试试火柴是否好用.小龙回家后,高兴地告诉妈妈:“火柴好用,我每根都试过了.”
(1)小龙采取的是哪种调查?
【解】小龙采取的是普查.
返回
(2)你认为小龙采取的方法是否合适?请说明理由.
【解】小龙采取的方法不合适,因为具有破坏性,所以应用抽样调查.
7.某食品加工厂有5条生产线,每条生产线一天能出产品20箱.质检员将对某日产品进行抽检,下列抽检方案中,最适宜的是( )
A.在该日的100箱产品中随机抽取1箱
B.抽取该日每条生产线的最后1箱产品
C.在该日每条生产线的产品中随机抽取1箱
D.抽取该日其中一条生产线的20箱产品
C
返回
样本估计总体
简单随机抽样
样本估计总体
1.样本具有代表性
2.用抽签的办法决定哪些个体进入样本
样本容量较大,可以用样本估计总体.
谢谢观看!
