28.3.1 借助调查作决策 课件(共24张PPT)
文档属性
| 名称 | 28.3.1 借助调查作决策 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
28.3.1 借助调查作决策
第28章 样本与总体
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握运用实验获取数据信息的方法,会用所学统计知识读取媒体信息,从中提取正确的信息
2.对提取的信息进行适当合理的分析,作出决策.
练习过程中,让学生独立完成,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
总体、个体、样本、样本容量的概念。请学生用自己的语言表述这些概念,并举例说明。
抽样调查的必要性及常见的抽样方法,如简单随机抽样和分层抽样的特点和应用。
用样本统计量估计总体特征的方法和注意事项。
强调重点和易错点,鼓励学生在课后多观察生活中的统计现象,运用所学知识进行分析。
(六)布置作业(5 分钟)
基础作业
为了解某班学生的数学成绩情况,从该班 50 名学生中抽取 10 名学生的数学成绩进行分析。指出这个问题中的总体、个体、样本和样本容量。
某果园有苹果树 1000 棵,为了解这些苹果树的产量情况,从中抽取了 50 棵苹果树的产量进行统计分析。若这 50 棵苹果树的平均产量为 80 千克,估计该果园苹果的总产量。
某学校有教师 150 人,其中高级教师 30 人,中级教师 90 人,初级教师 30 人。现采用分层抽样的方法抽取一个容量为 30 的样本,求从高级、中级、初级教师中分别抽取的人数。
拓展作业
设计一个调查方案,了解你所在社区居民对垃圾分类的知晓率和参与度。要求明确总体、个体、样本、样本容量及抽样方法。
实践作业
选择一个自己感兴趣的统计问题,如调查同学们喜欢的音乐类型、手机品牌等,进行数据收集和分析,并撰写一份简单的统计报告。
五、教学反思
在本节课的教学中,通过丰富的生活实例引导学生理解样本与总体的相关概念,学生对知识的接受度较好。小组合作探究和实践操作活动让学生积极参与到课堂中,提高了学生的动手能力和合作能力。但在教学过程中,对于抽样方法的实际应用,部分学生可能理解不够深入,在今后的教学中,可以增加更多实际案例的分析和讨论,让学生更好地掌握抽样方法的选择和应用。同时,要进一步加强对学生实践活动的指导,提高学生数据收集和分析的准确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
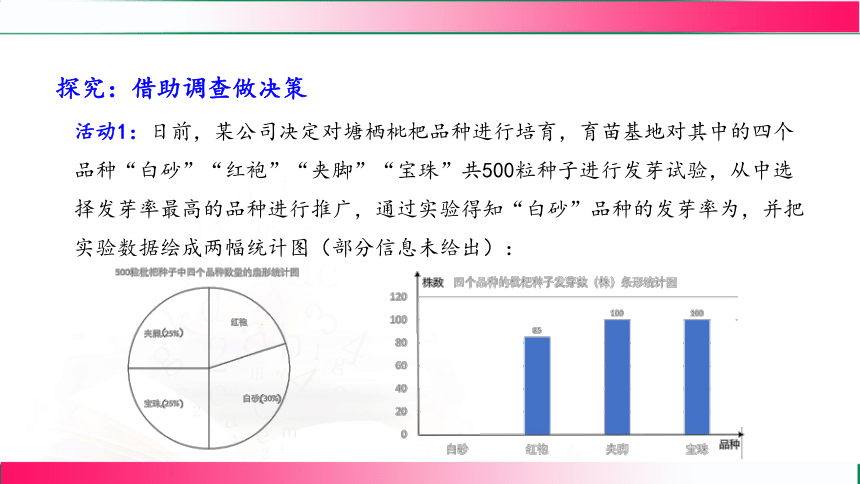
活动1:日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为,并把实验数据绘成两幅统计图(部分信息未给出):
探究:借助调查做决策
问题2:求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
“红袍”品种的种子数量: (株)
“白砂”品种的种子发芽的株数: (株)
补全条形统计图如图:
问题1:实验中“红袍”品种的种子数量是多少?
问题3:从以上信息,你认为应选哪一个品种进行推广,请说明理由.
“红袍”品种的种子发芽率:
“宝珠”品种的种子发芽率:
“夹脚”品种的种子发芽率:
因此,应该选择“红袍”品种进行推广.
活动2:一家冷饮厂做广告,说他们厂生产的雪糕在小棍上印有四种图案,集齐四种印有不同图案的小木棍能够组成一幅图,凭此可以在制定的商店领取一份奖品.假设该厂准备的印有四种图案的小木棍一样多,而且每支雪糕中夹入印有哪种图案的小木棍也是随机的.
想一想:有人买了4只就得奖了,有人买了20只都没有得奖,那么,平均要买多少支雪糕才能得奖呢?
在四张同样的小纸条上分别写上1、2、3、4,代表印有这四种图案的小木棍,随机抽出1张, 记录下每次抽到的数字,直到四个数字都出现,就算完成一次游戏,
即集齐了是跟印有不同图案的小木棍.记录下本次游戏中抽签的总次数,它代表本次中奖共买了多少支雪糕,下表是小明10次游戏的数据记录.
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
3 1 3 2 3 3 4 1 2 2 4 4 1 3 3
4 4 1 4 1 1 3 1 2 1 4 4 1
2 1 3 4 2 4 2 1 1 3 3
3 4 1 4 2 1 3 4 2 3 2
2 2 1 2 1 4 1 1 2 4
1 3 3 1 2 1 3 4 4
6支 6支 8支 5支 7支 6支 10支 6支 7支 8支
思考:有人得出来的结果是平均要买10支雪糕才能得奖,结果为什么会不一样?
因为
(支)
大约平均买七支雪糕才能得奖
归纳总结
通过实验去估计答案,要注意两点:
①不同的人得到的答案不一定相同,即使同一个人再进行相同次数的实验答案也不一定相同;
②要想答案尽可能准确,我们可以将实验次数尽可能地增加(但也要考虑到有无必要及可能性).因为实验次数充分大时,这个“平均数”将趋于稳定.
返回
1.下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:cm)的平均数和方差,要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是( )
A.甲 B.乙 C.丙 D.丁
C
甲 乙 丙 丁
平均数x(cm) 376 350 376 350
方差s2 12.5 13.5 2.4 5.4
2. 某服装店的某款衣服最近销售火爆,现有A,B两家供应商到服装店推销服装,两家服装价格相同,品质相近,服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ. A供应商供应材料的纯度(单位:%)如下:
Ⅱ. B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75
76 77 71 78 79 72 75
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅲ. A,B两家供应商供应材料纯度的平均数(单位:%)、中位数(单位:%)、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a 75 b c
根据以上信息,回答下列问题:
(1)表格中的a=________,b=________,c=________.
75
75
6
(2)你认为服装店应选择哪家供应商的服装?为什么?
【解】选择A供应商的服装.理由如下:
∵A,B平均数一样,B的方差比A的大,∴A更稳定,
∴选择A供应商的服装.
返回
3. 尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:
演员1 演员2 演员3 演员4 演员5 演员6 演员7 演员8
节目A √ √ √ √ √
节目B √ √ √
节目C √ √ √
节目D √ √
节目E √ √
节目F √ √
EBDC(或ECDB)
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序_______________(只需按演出顺序填写中间4个节目的字母即可).
【点拨】由题意得,首尾两个节目分别是A,F,节目A参演演员有1,3,5,6,8,节目F参演演员有5,7,由于从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,
故可先确定第二个节目为不含演员1,3,5,6,8的节目,即节目E;
第三个节目为不含演员2,7的节目,即节目B或C;
第五个节目为不含演员5,7的节目,即节目B或C;
所以,可确定第四个节目为节目D.
综上,演出顺序为节目AEBDCF或AECDBF.
故答案为EBDC或ECDB(写一种即可).
返回
借助调查做决策
通过实验获取数据
通过媒体获取数据
实验次数尽可能地多,所得“平均数”更准确.
结合实际情况加以分析
谢谢观看!
28.3.1 借助调查作决策
第28章 样本与总体
华东师大版数学九年级下册【示范课课件】
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握运用实验获取数据信息的方法,会用所学统计知识读取媒体信息,从中提取正确的信息
2.对提取的信息进行适当合理的分析,作出决策.
练习过程中,让学生独立完成,教师巡视指导,及时纠正学生的错误。
(五)课堂小结(5 分钟)
与学生一起回顾本节课所学内容:
总体、个体、样本、样本容量的概念。请学生用自己的语言表述这些概念,并举例说明。
抽样调查的必要性及常见的抽样方法,如简单随机抽样和分层抽样的特点和应用。
用样本统计量估计总体特征的方法和注意事项。
强调重点和易错点,鼓励学生在课后多观察生活中的统计现象,运用所学知识进行分析。
(六)布置作业(5 分钟)
基础作业
为了解某班学生的数学成绩情况,从该班 50 名学生中抽取 10 名学生的数学成绩进行分析。指出这个问题中的总体、个体、样本和样本容量。
某果园有苹果树 1000 棵,为了解这些苹果树的产量情况,从中抽取了 50 棵苹果树的产量进行统计分析。若这 50 棵苹果树的平均产量为 80 千克,估计该果园苹果的总产量。
某学校有教师 150 人,其中高级教师 30 人,中级教师 90 人,初级教师 30 人。现采用分层抽样的方法抽取一个容量为 30 的样本,求从高级、中级、初级教师中分别抽取的人数。
拓展作业
设计一个调查方案,了解你所在社区居民对垃圾分类的知晓率和参与度。要求明确总体、个体、样本、样本容量及抽样方法。
实践作业
选择一个自己感兴趣的统计问题,如调查同学们喜欢的音乐类型、手机品牌等,进行数据收集和分析,并撰写一份简单的统计报告。
五、教学反思
在本节课的教学中,通过丰富的生活实例引导学生理解样本与总体的相关概念,学生对知识的接受度较好。小组合作探究和实践操作活动让学生积极参与到课堂中,提高了学生的动手能力和合作能力。但在教学过程中,对于抽样方法的实际应用,部分学生可能理解不够深入,在今后的教学中,可以增加更多实际案例的分析和讨论,让学生更好地掌握抽样方法的选择和应用。同时,要进一步加强对学生实践活动的指导,提高学生数据收集和分析的准确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
活动1:日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为,并把实验数据绘成两幅统计图(部分信息未给出):
探究:借助调查做决策
问题2:求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
“红袍”品种的种子数量: (株)
“白砂”品种的种子发芽的株数: (株)
补全条形统计图如图:
问题1:实验中“红袍”品种的种子数量是多少?
问题3:从以上信息,你认为应选哪一个品种进行推广,请说明理由.
“红袍”品种的种子发芽率:
“宝珠”品种的种子发芽率:
“夹脚”品种的种子发芽率:
因此,应该选择“红袍”品种进行推广.
活动2:一家冷饮厂做广告,说他们厂生产的雪糕在小棍上印有四种图案,集齐四种印有不同图案的小木棍能够组成一幅图,凭此可以在制定的商店领取一份奖品.假设该厂准备的印有四种图案的小木棍一样多,而且每支雪糕中夹入印有哪种图案的小木棍也是随机的.
想一想:有人买了4只就得奖了,有人买了20只都没有得奖,那么,平均要买多少支雪糕才能得奖呢?
在四张同样的小纸条上分别写上1、2、3、4,代表印有这四种图案的小木棍,随机抽出1张, 记录下每次抽到的数字,直到四个数字都出现,就算完成一次游戏,
即集齐了是跟印有不同图案的小木棍.记录下本次游戏中抽签的总次数,它代表本次中奖共买了多少支雪糕,下表是小明10次游戏的数据记录.
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
3 1 3 2 3 3 4 1 2 2 4 4 1 3 3
4 4 1 4 1 1 3 1 2 1 4 4 1
2 1 3 4 2 4 2 1 1 3 3
3 4 1 4 2 1 3 4 2 3 2
2 2 1 2 1 4 1 1 2 4
1 3 3 1 2 1 3 4 4
6支 6支 8支 5支 7支 6支 10支 6支 7支 8支
思考:有人得出来的结果是平均要买10支雪糕才能得奖,结果为什么会不一样?
因为
(支)
大约平均买七支雪糕才能得奖
归纳总结
通过实验去估计答案,要注意两点:
①不同的人得到的答案不一定相同,即使同一个人再进行相同次数的实验答案也不一定相同;
②要想答案尽可能准确,我们可以将实验次数尽可能地增加(但也要考虑到有无必要及可能性).因为实验次数充分大时,这个“平均数”将趋于稳定.
返回
1.下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位:cm)的平均数和方差,要从中选择一名成绩较高且发挥稳定的运动员参加决赛,最合适的运动员是( )
A.甲 B.乙 C.丙 D.丁
C
甲 乙 丙 丁
平均数x(cm) 376 350 376 350
方差s2 12.5 13.5 2.4 5.4
2. 某服装店的某款衣服最近销售火爆,现有A,B两家供应商到服装店推销服装,两家服装价格相同,品质相近,服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析,部分信息如下:
Ⅰ. A供应商供应材料的纯度(单位:%)如下:
Ⅱ. B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75
76 77 71 78 79 72 75
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅲ. A,B两家供应商供应材料纯度的平均数(单位:%)、中位数(单位:%)、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a 75 b c
根据以上信息,回答下列问题:
(1)表格中的a=________,b=________,c=________.
75
75
6
(2)你认为服装店应选择哪家供应商的服装?为什么?
【解】选择A供应商的服装.理由如下:
∵A,B平均数一样,B的方差比A的大,∴A更稳定,
∴选择A供应商的服装.
返回
3. 尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:
演员1 演员2 演员3 演员4 演员5 演员6 演员7 演员8
节目A √ √ √ √ √
节目B √ √ √
节目C √ √ √
节目D √ √
节目E √ √
节目F √ √
EBDC(或ECDB)
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序_______________(只需按演出顺序填写中间4个节目的字母即可).
【点拨】由题意得,首尾两个节目分别是A,F,节目A参演演员有1,3,5,6,8,节目F参演演员有5,7,由于从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,
故可先确定第二个节目为不含演员1,3,5,6,8的节目,即节目E;
第三个节目为不含演员2,7的节目,即节目B或C;
第五个节目为不含演员5,7的节目,即节目B或C;
所以,可确定第四个节目为节目D.
综上,演出顺序为节目AEBDCF或AECDBF.
故答案为EBDC或ECDB(写一种即可).
返回
借助调查做决策
通过实验获取数据
通过媒体获取数据
实验次数尽可能地多,所得“平均数”更准确.
结合实际情况加以分析
谢谢观看!
