27.2.1 相似三角形的判定(第1课时) 课件(共28张PPT)
文档属性
| 名称 | 27.2.1 相似三角形的判定(第1课时) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 21:30:26 | ||
图片预览







文档简介
(共34张PPT)
27.2.1 相似三角形的判定
(第1课时)
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
理解相似三角形的概念,并会用以证明和计算.
体会用相似符号“∽”表示的相似三角形之间的边,角对应关系.
掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
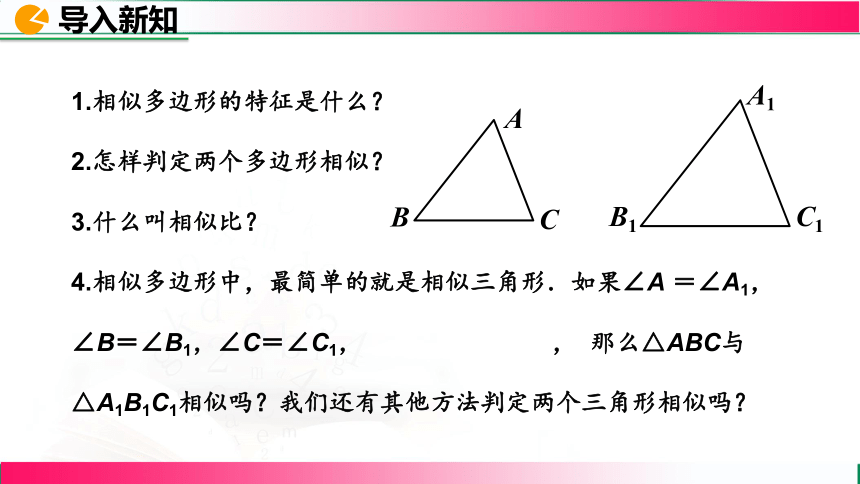
1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A =∠A1,
∠B=∠B1,∠C=∠C1, , 那么△ABC与
△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
导入新知
A
B
C
A1
B1
C1
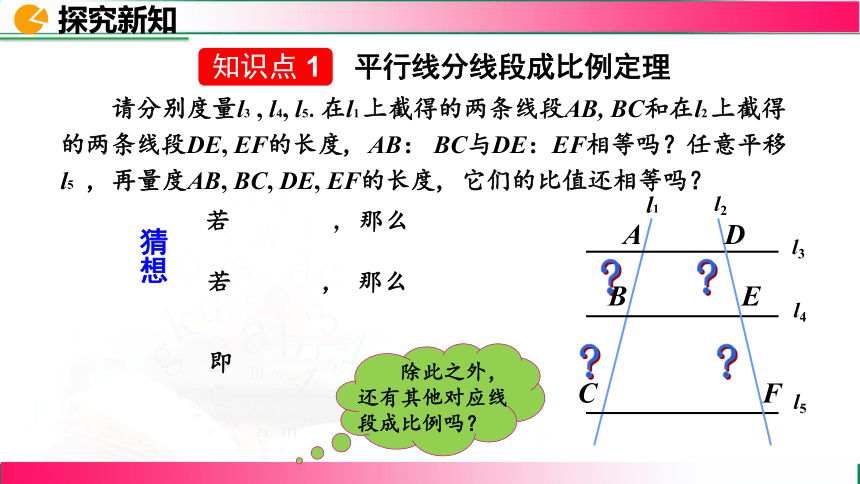
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗?
猜想
A
B
C
D
E
F
l2
探究新知
l1
除此之外,还有其他对应线段成比例吗?
l2
l3
l4
l5
知识点 1
平行线分线段成比例定理
若 ,那么
若 , 那么
即
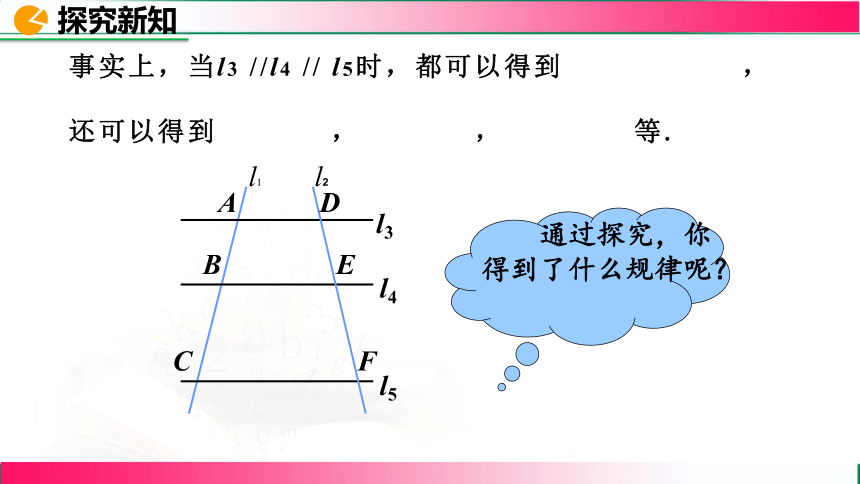
事实上,当l3 //l4 // l5时,都可以得到 ,
还可以得到 , , 等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
通过探究,你得到了什么规律呢?
探究新知
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥ c ,则 , ,
归纳:
A1
A2
A3
B1
B2
B3
b
c
a
探究新知
1. 如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
【想一想】
探究新知
如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
巩固练习
如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A
B
C
D
E
F
l4
l5
l1
l2
l3
把直线 l1向左或向右任意平移,这些线段依然成比例.
探究新知
知识点 2
平行线分线段成比例定理的推论
【思考】
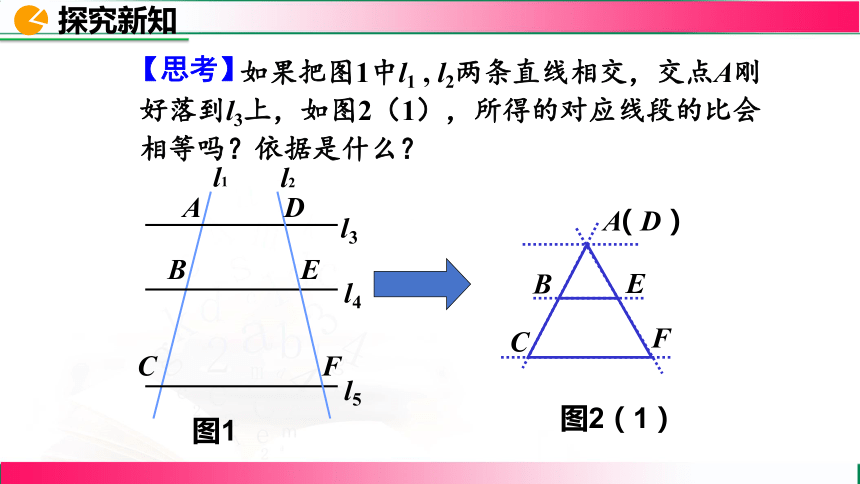
如果把图1中l1 , l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
探究新知
图1
图2(1)
A
(D)
E
F
C
B
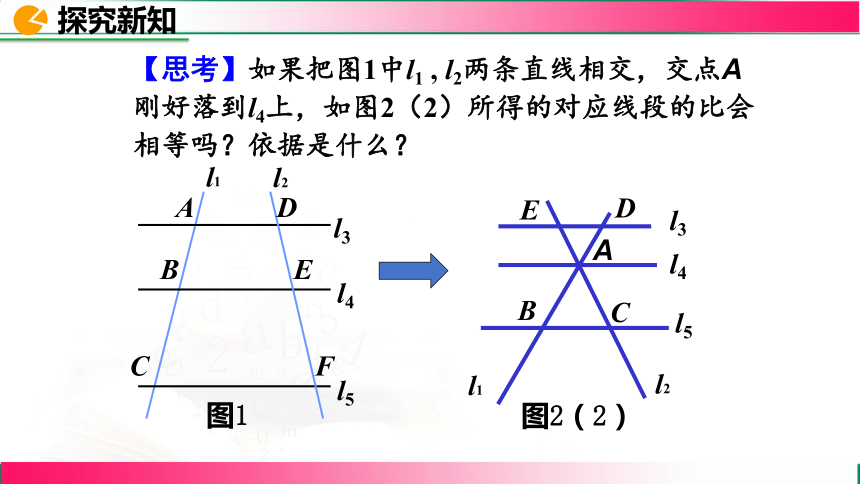
【思考】如果把图1中l1 , l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
探究新知
图1
图2(2)
A
B
C
D
E
F
l3
l4
l5
l1
l2
B
C
E
A
D
l1
l2
l3
l4
l5
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
探究新知
归纳:
巩固练习
如图,l1∥l2∥l3, ,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴ .
又∵ ,DE=6,
∴ ,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
探究新知
考点 1 1
利用平行线分线段成比例定理及推论求线段长度
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,FC=3cm,AF的长为_______.
1cm
巩固练习
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1 △ADE与△ABC的三个角分别相等吗?
问题2 分别度量△ADE与△ABC的边长,它们的边
长是否对应成比例?
B
C
A
D
E
探究新知
知识点 3
相似三角形的判定定理
问题3 你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
探究新知
B
C
A
D
E
【思考】1.我们通过度量三角形的边长,知道△ADE∽
△ABC,但要用相似的定义去证明它,我们需要证明什么?
2.由前面的结论,我们可以得到什么?还需证明什么?
探究新知
用相似的定义证明△ADE∽△ABC
B
C
A
D
E
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF .
∴△ADE∽△ABC .
探究新知
∴ .
∴ .
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB , AC于点D、E.
求证:△ADE∽△ABC .
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
探究新知
定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.
符号语言:
∵ DE//BC,
∴△ADE∽△ABC.
【讨论】过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
【方法总结】过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
探究新知
已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
相似具有传递性
巩固练习
B
返回
1.
已知△ABC∽△DEF,AB=2,BC=3,若DE=3,
则EF=( )
A.6
B.4.5
C.5
D.2.5
返回
C
2.
[2024重庆一中月考]如图,l1∥l2∥l3,直线a,b相交于点G,与这三条平行线分别相交于点A,B,C和点D,E,F,下列比例式中错误的是( )
3.
[2024长春]如图,在△ABC中,O是边AB的中点.按下列要求作图: ①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G ,点G与点C在直线AB的同侧;④作直线OG,交AC于点M.
D
返回
4.
返回
B
[2024河南]如图,在 ABCD中,对角线AC,BD相交于点O,E为OC的中点,EF∥AB交BC于点F.若 AB=4,则EF的长为( )
5.
(2)若CD=2,在上述条件和结论下,求EF的长.
返回
6.
返回
B
7.
[2024宣城期末]如图,在梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7
B.5:7
C.3:7
D.2:5
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
课堂小结
谢谢观看!
27.2.1 相似三角形的判定
(第1课时)
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
理解相似三角形的概念,并会用以证明和计算.
体会用相似符号“∽”表示的相似三角形之间的边,角对应关系.
掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A =∠A1,
∠B=∠B1,∠C=∠C1, , 那么△ABC与
△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
导入新知
A
B
C
A1
B1
C1
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB: BC与DE:EF相等吗?任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗?
猜想
A
B
C
D
E
F
l2
探究新知
l1
除此之外,还有其他对应线段成比例吗?
l2
l3
l4
l5
知识点 1
平行线分线段成比例定理
若 ,那么
若 , 那么
即
事实上,当l3 //l4 // l5时,都可以得到 ,
还可以得到 , , 等.
A
B
C
D
E
F
l3
l4
l5
l1
l2
通过探究,你得到了什么规律呢?
探究新知
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥ c ,则 , ,
归纳:
A1
A2
A3
B1
B2
B3
b
c
a
探究新知
1. 如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
【想一想】
探究新知
如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
巩固练习
如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A
B
C
D
E
F
l4
l5
l1
l2
l3
把直线 l1向左或向右任意平移,这些线段依然成比例.
探究新知
知识点 2
平行线分线段成比例定理的推论
【思考】
如果把图1中l1 , l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
A
B
C
D
E
F
l3
l4
l5
l1
l2
探究新知
图1
图2(1)
A
(D)
E
F
C
B
【思考】如果把图1中l1 , l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
探究新知
图1
图2(2)
A
B
C
D
E
F
l3
l4
l5
l1
l2
B
C
E
A
D
l1
l2
l3
l4
l5
l2
l3
l1
l3
l
l
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l
探究新知
归纳:
巩固练习
如图,l1∥l2∥l3, ,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴ .
又∵ ,DE=6,
∴ ,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
探究新知
考点 1 1
利用平行线分线段成比例定理及推论求线段长度
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,FC=3cm,AF的长为_______.
1cm
巩固练习
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
问题1 △ADE与△ABC的三个角分别相等吗?
问题2 分别度量△ADE与△ABC的边长,它们的边
长是否对应成比例?
B
C
A
D
E
探究新知
知识点 3
相似三角形的判定定理
问题3 你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,
且只要DE∥BC,这个结论恒成立.
探究新知
B
C
A
D
E
【思考】1.我们通过度量三角形的边长,知道△ADE∽
△ABC,但要用相似的定义去证明它,我们需要证明什么?
2.由前面的结论,我们可以得到什么?还需证明什么?
探究新知
用相似的定义证明△ADE∽△ABC
B
C
A
D
E
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF .
∴△ADE∽△ABC .
探究新知
∴ .
∴ .
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB , AC于点D、E.
求证:△ADE∽△ABC .
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
探究新知
定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.
符号语言:
∵ DE//BC,
∴△ADE∽△ABC.
【讨论】过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?
【方法总结】过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
探究新知
已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
3
C
D
A
B
E
F
O
相似具有传递性
巩固练习
B
返回
1.
已知△ABC∽△DEF,AB=2,BC=3,若DE=3,
则EF=( )
A.6
B.4.5
C.5
D.2.5
返回
C
2.
[2024重庆一中月考]如图,l1∥l2∥l3,直线a,b相交于点G,与这三条平行线分别相交于点A,B,C和点D,E,F,下列比例式中错误的是( )
3.
[2024长春]如图,在△ABC中,O是边AB的中点.按下列要求作图: ①以点B为圆心、适当长为半径画弧,交线段BO于点D,交BC于点E;②以点O为圆心、BD长为半径画弧,交线段OA于点F;③以点F为圆心、DE长为半径画弧,交前一条弧于点G ,点G与点C在直线AB的同侧;④作直线OG,交AC于点M.
D
返回
4.
返回
B
[2024河南]如图,在 ABCD中,对角线AC,BD相交于点O,E为OC的中点,EF∥AB交BC于点F.若 AB=4,则EF的长为( )
5.
(2)若CD=2,在上述条件和结论下,求EF的长.
返回
6.
返回
B
7.
[2024宣城期末]如图,在梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7
B.5:7
C.3:7
D.2:5
两条直线被一组平行线所截,所得的对应线段成比例.
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实
平行线分线段成比例定理及其推论
课堂小结
谢谢观看!
