27.2.1 相似三角形的判定(第2课时) 课件(共28张PPT)
文档属性
| 名称 | 27.2.1 相似三角形的判定(第2课时) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 21:31:14 | ||
图片预览





文档简介
(共28张PPT)
27.2.1 相似三角形的判定
(第2课时)
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
复习已经学过的三角形相似的判定定理 .
会运用“三组对应边的比相等的两个三角形相似”判定两个三角形相似,并能进行相关计算与推理.
培养学生探究交流能力,发展推理能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
探究探究!
讨论一下?
导入新知
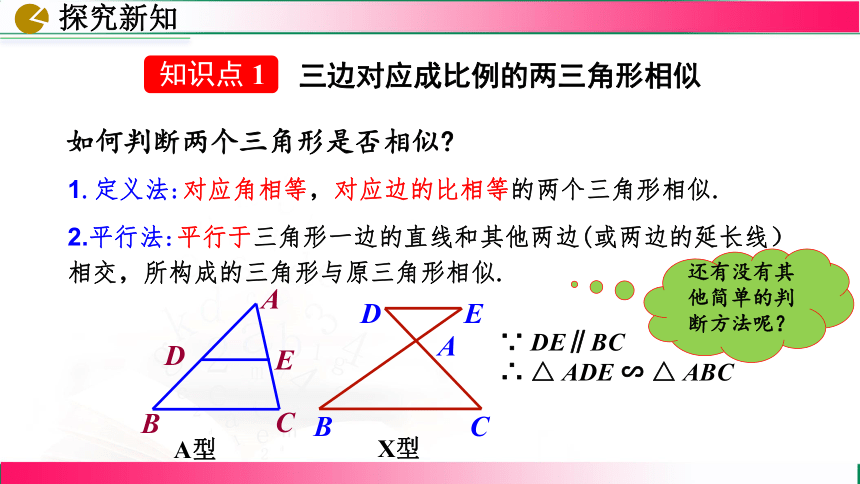
1.定义法:对应角相等,对应边的比相等的两个三角形相似.
如何判断两个三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
D
E
A
B
C
A
B
C
D
E
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
A型
X型
探究新知
知识点 1
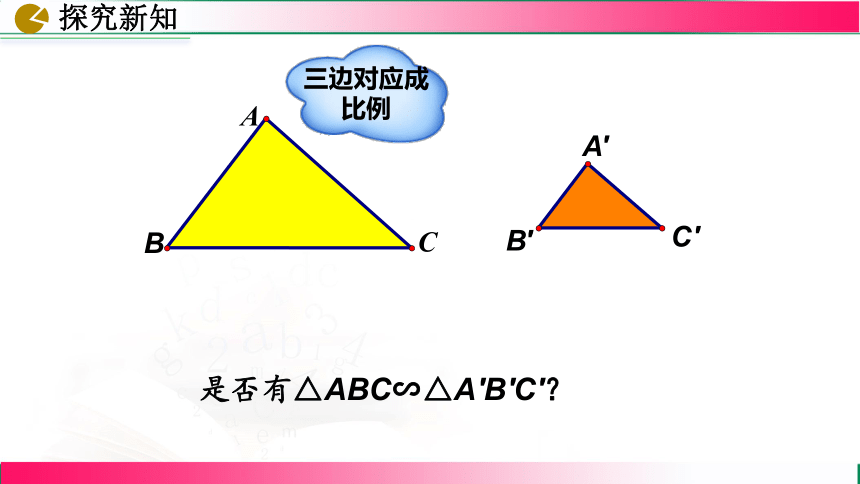
三边对应成比例的两三角形相似
还有没有其他简单的判断方法呢?
是否有△ABC∽△A′B′C′?
A
B
C
三边对应成比例
探究新知
C′
B′
A′
A
B
C
C′
B′
A′
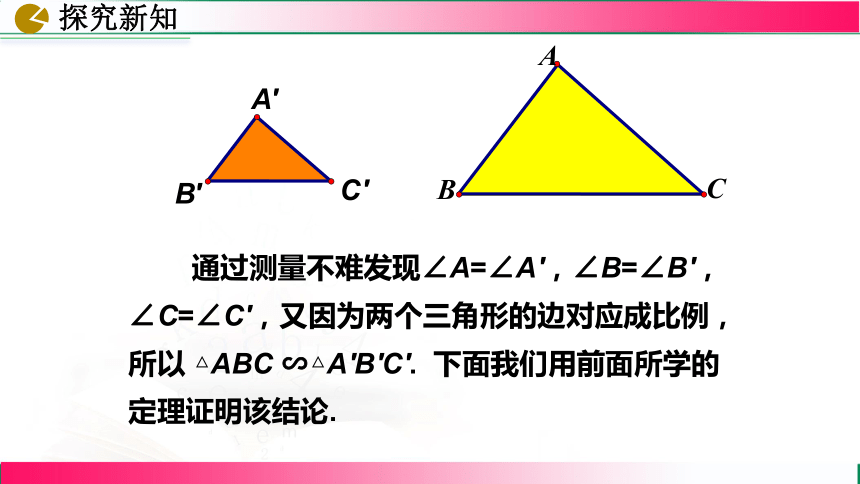
通过测量不难发现∠A=∠A′,∠B=∠B′,∠C=∠C′,又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学的定理证明该结论.
探究新知
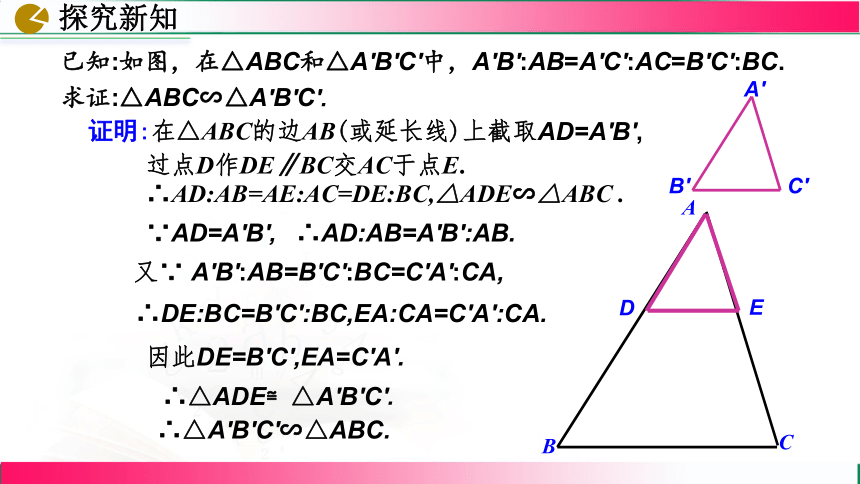
已知:如图,在△ABC和△A′B′C′中,A′B′:AB=A′C′:AC=B′C′:BC.
求证:△ABC∽△A′B′C′.
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又∵ A′B′:AB=B′C′:BC=C′A′:CA,
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC .
∵AD=A′B′, ∴AD:AB=A′B′:AB.
∴DE:BC=B′C′:BC,EA:CA=C′A′:CA.
因此DE=B′C′,EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′.
探究新知
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归纳:
∵ ,
∴ △ ABC ∽ △A′B′C.
符号语言:
探究新知
【讨论】在用三边的比判定两个三角形相似时,如何寻找对应边?
【总结】利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
探究新知
已知AB=4 cm,BC=6 cm ,AC=8 cm, A′B′ =12 cm , B′C′=18 cm , A′C′=24 cm ,试说明△ABC∽△ A′B′C′.
∴ △ABC∽△ A′B′C′. '
探究新知
考点 1
利用三边成比例判断三角形相似
解:∵
∴ .
探究新知
方法点拨
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最大边与最大边对应,最短边与最短边对应.
在△ABC和△DEF中,如果AB=4,BC=3,AC=6;DE=2.4,EF=1.2,FD=1.6,那么这两个三角形能否相似的结论是______,理由是_________________.
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
相似
C
三组对应边的比相等
巩固练习
A. ①和② B. ②和③ C. ①和③ D. ②和④
如图,在 Rt△ABC 与 Rt△A′B′C′中,∠C =∠C ′ = 90°,
且 求证:△ A′B′C′∽△ABC.
证明:由已知条件得 AB = 2 A′B′,AC = 2 A′C′,
∴ BC 2 = AB 2-AC 2 = ( 2 A′B′ )2-( 2 A′C′ )2 = 4 A′B′ 2-4 A′C′ 2
= 4 ( A′B′ 2-A′C′ 2 ) = 4 B′C′ 2 = ( 2 B′C′ )2.
∴ △ A′B′C′∽△ABC.
∴ BC=2B′C′,
探究新知
考点 2
判断三角形相似
如图,△ABC中,点 D,E,F 分别是 AB,BC,CA的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
巩固练习
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE.
如图已知:
解:∵
探究新知
考点 3
利用三角形相似说明角相等
解:相等的角有∠BAC=∠DAE,
∠B=∠ADE,∠C=∠E,∠BAD=∠CAE.
理由如下:
在 △ABC 和 △ADE 中,∵ AB : AD = BC : DE = AC : AE,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,∠B= ∠ADE ,∠C=∠E.
∴∠BAC-∠CAD =∠DAE-∠CAD ,
∴∠BAD=∠CAE.
故图中相等的角有∠BAC=∠DAE,
∠B=∠ADE,∠C=∠E,∠BAD=∠CAE.
如图,已知 AB : AD = BC : DE = AC : AE,找出图中相等的角 (对顶角除外),并说明你的理由.
A
B
C
D
E
巩固练习
C
返回
1.
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
2.
【点拨】
【答案】B
∵AD:AC=1:3,∴AD:DC=1:2.
∵△ABC是正三角形,∴∠A=∠C=60°,AB=BC=AC.
∵AE=BE,∴AE:BC=AE:AB=1:2.
∴AD:DC=AE:BC.
又∵∠A=∠C,∴△AED∽△CBD.故选B.
返回
3.
在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似,“马”应落在( )
A.①处 B.②处
C.③处 D.④处
【点拨】
【答案】B
返回
4.
如图,BD平分∠ABC,且AB=4,BC=6,则当BD=________时,△ABD∽△DBC.
【点拨】
【点易错】
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么这两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
. . .
返回
5.
返回
[2024广州]如图,点E,F分别在正方形ABCD的边BC,CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
6.
一个三角形木架的三边长分别是75 cm,100 cm,
120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
三边成比例两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
谢谢观看!
27.2.1 相似三角形的判定
(第2课时)
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
复习已经学过的三角形相似的判定定理 .
会运用“三组对应边的比相等的两个三角形相似”判定两个三角形相似,并能进行相关计算与推理.
培养学生探究交流能力,发展推理能力.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
探究探究!
讨论一下?
导入新知
1.定义法:对应角相等,对应边的比相等的两个三角形相似.
如何判断两个三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
D
E
A
B
C
A
B
C
D
E
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
A型
X型
探究新知
知识点 1
三边对应成比例的两三角形相似
还有没有其他简单的判断方法呢?
是否有△ABC∽△A′B′C′?
A
B
C
三边对应成比例
探究新知
C′
B′
A′
A
B
C
C′
B′
A′
通过测量不难发现∠A=∠A′,∠B=∠B′,∠C=∠C′,又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学的定理证明该结论.
探究新知
已知:如图,在△ABC和△A′B′C′中,A′B′:AB=A′C′:AC=B′C′:BC.
求证:△ABC∽△A′B′C′.
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A′
B′
C′
A
B
C
D
E
过点D作DE∥BC交AC于点E.
又∵ A′B′:AB=B′C′:BC=C′A′:CA,
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC .
∵AD=A′B′, ∴AD:AB=A′B′:AB.
∴DE:BC=B′C′:BC,EA:CA=C′A′:CA.
因此DE=B′C′,EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′.
探究新知
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归纳:
∵ ,
∴ △ ABC ∽ △A′B′C.
符号语言:
探究新知
【讨论】在用三边的比判定两个三角形相似时,如何寻找对应边?
【总结】利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
探究新知
已知AB=4 cm,BC=6 cm ,AC=8 cm, A′B′ =12 cm , B′C′=18 cm , A′C′=24 cm ,试说明△ABC∽△ A′B′C′.
∴ △ABC∽△ A′B′C′. '
探究新知
考点 1
利用三边成比例判断三角形相似
解:∵
∴ .
探究新知
方法点拨
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最大边与最大边对应,最短边与最短边对应.
在△ABC和△DEF中,如果AB=4,BC=3,AC=6;DE=2.4,EF=1.2,FD=1.6,那么这两个三角形能否相似的结论是______,理由是_________________.
如图,在大小为4×4的正方形网格中,是相似三角形的是( )
相似
C
三组对应边的比相等
巩固练习
A. ①和② B. ②和③ C. ①和③ D. ②和④
如图,在 Rt△ABC 与 Rt△A′B′C′中,∠C =∠C ′ = 90°,
且 求证:△ A′B′C′∽△ABC.
证明:由已知条件得 AB = 2 A′B′,AC = 2 A′C′,
∴ BC 2 = AB 2-AC 2 = ( 2 A′B′ )2-( 2 A′C′ )2 = 4 A′B′ 2-4 A′C′ 2
= 4 ( A′B′ 2-A′C′ 2 ) = 4 B′C′ 2 = ( 2 B′C′ )2.
∴ △ A′B′C′∽△ABC.
∴ BC=2B′C′,
探究新知
考点 2
判断三角形相似
如图,△ABC中,点 D,E,F 分别是 AB,BC,CA的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,CA的中点,
∴
∴
巩固练习
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE.
如图已知:
解:∵
探究新知
考点 3
利用三角形相似说明角相等
解:相等的角有∠BAC=∠DAE,
∠B=∠ADE,∠C=∠E,∠BAD=∠CAE.
理由如下:
在 △ABC 和 △ADE 中,∵ AB : AD = BC : DE = AC : AE,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,∠B= ∠ADE ,∠C=∠E.
∴∠BAC-∠CAD =∠DAE-∠CAD ,
∴∠BAD=∠CAE.
故图中相等的角有∠BAC=∠DAE,
∠B=∠ADE,∠C=∠E,∠BAD=∠CAE.
如图,已知 AB : AD = BC : DE = AC : AE,找出图中相等的角 (对顶角除外),并说明你的理由.
A
B
C
D
E
巩固练习
C
返回
1.
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
2.
【点拨】
【答案】B
∵AD:AC=1:3,∴AD:DC=1:2.
∵△ABC是正三角形,∴∠A=∠C=60°,AB=BC=AC.
∵AE=BE,∴AE:BC=AE:AB=1:2.
∴AD:DC=AE:BC.
又∵∠A=∠C,∴△AED∽△CBD.故选B.
返回
3.
在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似,“马”应落在( )
A.①处 B.②处
C.③处 D.④处
【点拨】
【答案】B
返回
4.
如图,BD平分∠ABC,且AB=4,BC=6,则当BD=________时,△ABD∽△DBC.
【点拨】
【点易错】
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么这两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
. . .
返回
5.
返回
[2024广州]如图,点E,F分别在正方形ABCD的边BC,CD上,BE=3,EC=6,CF=2.求证:△ABE∽△ECF.
6.
一个三角形木架的三边长分别是75 cm,100 cm,
120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
三边成比例两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
谢谢观看!
