27.2.2 相似三角形的性质 课件(共41张PPT)
文档属性
| 名称 | 27.2.2 相似三角形的性质 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 21:34:28 | ||
图片预览







文档简介
(共41张PPT)
27.2.2 相似三角形的性质
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
在理解相似三角形特征的基础上,掌握相似三角形对应高、对应中线、对应角平分线、周长、面积的比等性质,并运用其进行计算与推理.
通过实践体会相似三角形的性质,会用性质与判定解决相关的问题.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
相似三角形的判定方法有哪几种?
1.对应边成比例,对应角相等的两个三角形相似.
2.平行于三角形一边,与另外两边相交所构成的三
角形与原三角形相似.
3. 三边对应成比例的两三角形相似.
4. 两边成比例且夹角相等的两个三角形相似.
5. 两角分别相等的两个三角形相似.
6. 两边对应成比例的两直角三角形相似.
导入新知
三角形除了三个角,三条边外,还有哪些几何量
【思考】如果两个三角形相似,那么它们的这些几何量有一些怎样的性质呢
高线
角平分线
中线
面积
周长
导入新知
A
B
C
A'
B'
C'
探究新知
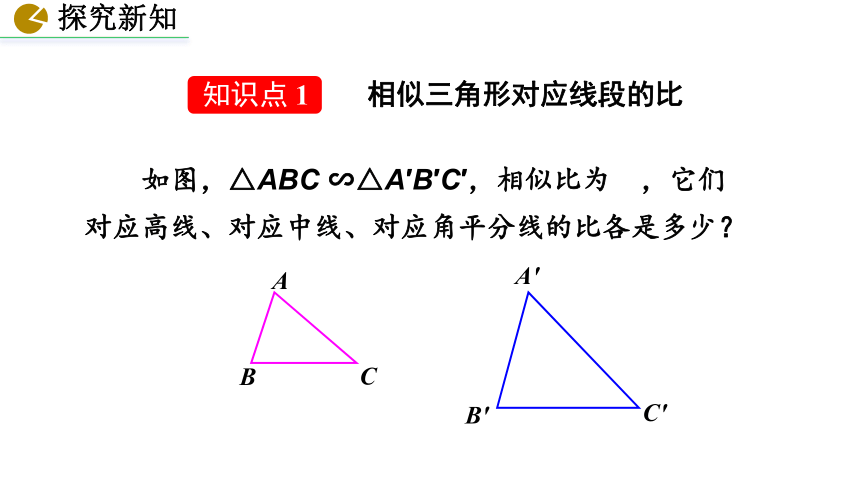
知识点 1
相似三角形对应线段的比
如图,△ABC ∽△A′B′C′,相似比为 ,它们对应高线、对应中线、对应角平分线的比各是多少?
A
C
B
A′
B′
C′
(2)
探究新知
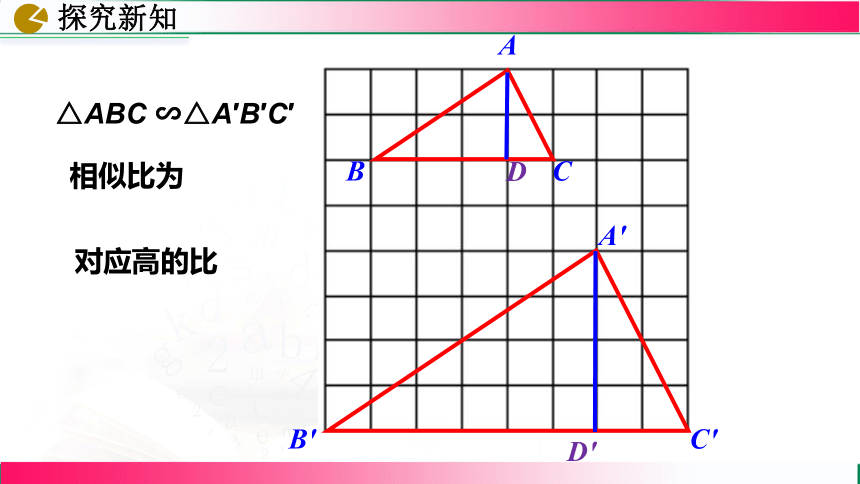
△ABC ∽△A′B′C′
相似比为
对应高的比
D′
D
C
A′
B′
C′
(1)
探究新知
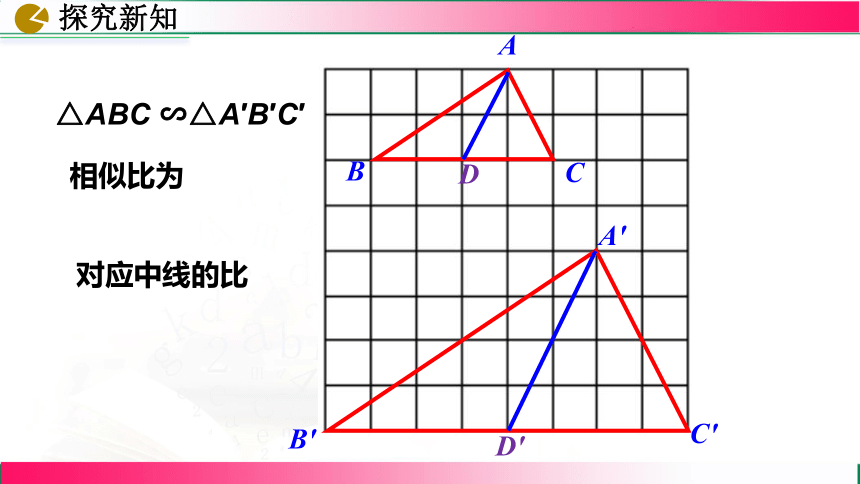
△ABC ∽△A′B′C′
相似比为
对应中线的比
D′
D
A
B
C
A′
B′
C′
(3)
探究新知
△ABC ∽△A′B′C′
相似比为
对应角平分线的比
D′
D
A
B
如图, △ABC ∽△A′B′C′ ,若相似比为k ,它们对应高、对应中线、对应角平分线的比又各是多少?
A
B
C
A'
B'
C'
探究新知
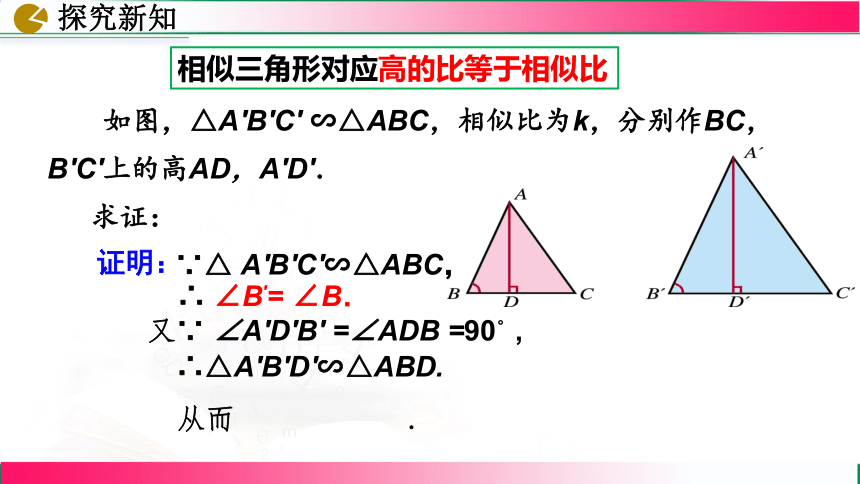
相似三角形对应高的比等于相似比
证明:
∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A'D′B' =∠ADB =90°,
∴△A′B′D′∽△ABD.
从而 .
如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
探究新知
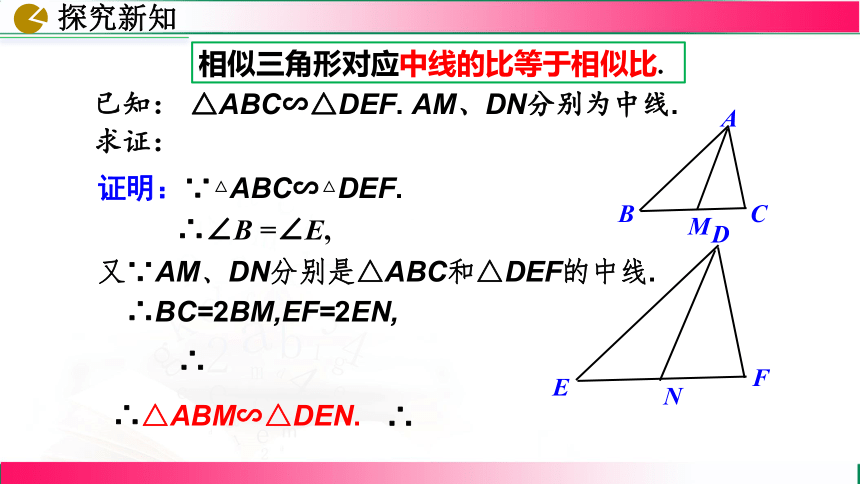
证明:∵△ABC∽△DEF.
相似三角形对应中线的比等于相似比.
A
B
C
M
D
E
F
N
又∵AM、DN分别是△ABC和△DEF的中线.
∴△ABM∽△DEN.
求证:
已知:
△ABC∽△DEF. AM、DN分别为中线.
探究新知
∴BC=2BM,EF=2EN,
∴
∴
∴∠B =∠E,
证明:∵△ABC∽△DEF.
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线.
相似三角形对应角平分线的比等于相似比.
A
B
C
M
D
E
F
N
求证:
已知:
△ABC∽△DEF. AM、DN分别为角平分线.
探究新知
∴
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴ , ,
相似三角形对应中线、角平分线的比也等于相似比.
相似三角形对应高的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
探究新知
归纳总结
解:∵ △ABC ∽△DEF,
D
E
F
H
已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG = 4.8 cm. 求 EH 的长.
∴ .
∴ ,解得 EH = 3.2.
A
G
B
C
故 EH 的长为 3.2 cm.
探究新知
考点 1 1
利用相似三角形对应线段的比求线段的长度
相似三角形对应边的比为2∶3,那么相似比为________,对应角的角平分线的比为 .
2∶ 3
2 ∶ 3
两个相似三角形对应边上的高的比为1∶4 , 若一个三角形的最长边是为12,则另一个三角形的最长边是_______.
3或48
巩固练习
相似三角形的周长比也等于相似比吗?为什么?
【想一想】
探究新知
知识点 2
相似三角形周长的比
相似三角形周长的比等于相似比.
已知:
求证:
证明1:
∴ .
∴
(等比性质).
A
C
B
B′
A′
C′
探究新知
∵△ABC ∽△A′B′C′,
△ABC ∽△A′B′C′.
A
B
C
证明2:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
探究新知
相似三角形的周长比等于相似比.
∵△ABC ∽△A′B′C′,
相似比为k.
∴ .
A′
B′
C′
相似三角形对应边的比为2∶5,那么周长比为________.
2∶5
两个相似三角形周长的比为1∶7 , 则它们的相似比为_______,对应边上角平分线的比为_______.
1∶7
1∶7
巩固练习
如图,△ABC ∽△A′B′C′,相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
探究新知
知识点 3
相似三角形面积的比
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
探究新知
==·=k· k= k2
∴
几何表述:
相似三角形性质定理:
相似三角形面积的比等于相似比的平方.
探究新知
∵△ABC ∽△A′B′C′,相似比为k ,
归纳:
∴ .
A′
B′
C′
A
B
C
已知两个三角形相似,请完成下列表格:
相似比 2 k ……
周长比 ……
面积比 10000 ……
2
4
100
100
k
k2
巩固练习
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
探究新知
考点 1
利用相似三角形面积的比求面积或线段
A
B
C
D
E
F
面积为
探究新知
∴△DEF 的边 EF 上的高为 ,
∵△ABC 的边 BC 上的高为 6,面积为 ,
如果两个相似三角形的面积之比为 4 : 9,较大三角形一边上的高为 18,则较小三角形对应边上的高为______.
巩固练习
12
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
考点 2
利用相似三角形面积的比求多边形的面积(比)
探究新知
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
如图,这是圆桌正上方的灯泡 (点A ) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6(米).
∵DF∥CH,∴△ADF ∽△ACH,
巩固练习
∴ 即
解得 CH = 0.9米.
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
巩固练习
∴ 阴影部分的面积为:
A
D
E
F
C
B
H
D
返回
1.
返回
A
2.
已知两个三角形相似,若它们的对应中线之比为2:3,则它们的周长比为( )
B
返回
3.
如果两个相似三角形的对应高线的长度之比为a:b,对应的角平分线的长度之比为b:a,那么( )
A.a>b
B.a=b
C.aD.a,b的大小无法比较
4.
[2024沈阳期末]如图是学生用具三角尺ABC,∠C=90°,∠B=30°,其中△DEF∽△ABC,AB长为12 cm,DF长为3 cm,则这个三角尺中△DEF与△ABC的面积比为( )
【点拨】
【答案】B
返回
5.
【点拨】
返回
6.
5
【点拨】
相似三角形的性质
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方
课堂小结
相似三角形周长的比等于相似比
谢谢观看!
27.2.2 相似三角形的性质
第二十七章 相似
人教版数学九年级下册
授课教师:********
班 级:********
时 间:********
学习目标
在理解相似三角形特征的基础上,掌握相似三角形对应高、对应中线、对应角平分线、周长、面积的比等性质,并运用其进行计算与推理.
通过实践体会相似三角形的性质,会用性质与判定解决相关的问题.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
相似三角形的判定方法有哪几种?
1.对应边成比例,对应角相等的两个三角形相似.
2.平行于三角形一边,与另外两边相交所构成的三
角形与原三角形相似.
3. 三边对应成比例的两三角形相似.
4. 两边成比例且夹角相等的两个三角形相似.
5. 两角分别相等的两个三角形相似.
6. 两边对应成比例的两直角三角形相似.
导入新知
三角形除了三个角,三条边外,还有哪些几何量
【思考】如果两个三角形相似,那么它们的这些几何量有一些怎样的性质呢
高线
角平分线
中线
面积
周长
导入新知
A
B
C
A'
B'
C'
探究新知
知识点 1
相似三角形对应线段的比
如图,△ABC ∽△A′B′C′,相似比为 ,它们对应高线、对应中线、对应角平分线的比各是多少?
A
C
B
A′
B′
C′
(2)
探究新知
△ABC ∽△A′B′C′
相似比为
对应高的比
D′
D
C
A′
B′
C′
(1)
探究新知
△ABC ∽△A′B′C′
相似比为
对应中线的比
D′
D
A
B
C
A′
B′
C′
(3)
探究新知
△ABC ∽△A′B′C′
相似比为
对应角平分线的比
D′
D
A
B
如图, △ABC ∽△A′B′C′ ,若相似比为k ,它们对应高、对应中线、对应角平分线的比又各是多少?
A
B
C
A'
B'
C'
探究新知
相似三角形对应高的比等于相似比
证明:
∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A'D′B' =∠ADB =90°,
∴△A′B′D′∽△ABD.
从而 .
如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
探究新知
证明:∵△ABC∽△DEF.
相似三角形对应中线的比等于相似比.
A
B
C
M
D
E
F
N
又∵AM、DN分别是△ABC和△DEF的中线.
∴△ABM∽△DEN.
求证:
已知:
△ABC∽△DEF. AM、DN分别为中线.
探究新知
∴BC=2BM,EF=2EN,
∴
∴
∴∠B =∠E,
证明:∵△ABC∽△DEF.
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线.
相似三角形对应角平分线的比等于相似比.
A
B
C
M
D
E
F
N
求证:
已知:
△ABC∽△DEF. AM、DN分别为角平分线.
探究新知
∴
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴ , ,
相似三角形对应中线、角平分线的比也等于相似比.
相似三角形对应高的比等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
探究新知
归纳总结
解:∵ △ABC ∽△DEF,
D
E
F
H
已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG = 4.8 cm. 求 EH 的长.
∴ .
∴ ,解得 EH = 3.2.
A
G
B
C
故 EH 的长为 3.2 cm.
探究新知
考点 1 1
利用相似三角形对应线段的比求线段的长度
相似三角形对应边的比为2∶3,那么相似比为________,对应角的角平分线的比为 .
2∶ 3
2 ∶ 3
两个相似三角形对应边上的高的比为1∶4 , 若一个三角形的最长边是为12,则另一个三角形的最长边是_______.
3或48
巩固练习
相似三角形的周长比也等于相似比吗?为什么?
【想一想】
探究新知
知识点 2
相似三角形周长的比
相似三角形周长的比等于相似比.
已知:
求证:
证明1:
∴ .
∴
(等比性质).
A
C
B
B′
A′
C′
探究新知
∵△ABC ∽△A′B′C′,
△ABC ∽△A′B′C′.
A
B
C
证明2:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
探究新知
相似三角形的周长比等于相似比.
∵△ABC ∽△A′B′C′,
相似比为k.
∴ .
A′
B′
C′
相似三角形对应边的比为2∶5,那么周长比为________.
2∶5
两个相似三角形周长的比为1∶7 , 则它们的相似比为_______,对应边上角平分线的比为_______.
1∶7
1∶7
巩固练习
如图,△ABC ∽△A′B′C′,相似比为k,它们的面积比是多少?
A
B
C
A'
B'
C'
探究新知
知识点 3
相似三角形面积的比
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
探究新知
==·=k· k= k2
∴
几何表述:
相似三角形性质定理:
相似三角形面积的比等于相似比的平方.
探究新知
∵△ABC ∽△A′B′C′,相似比为k ,
归纳:
∴ .
A′
B′
C′
A
B
C
已知两个三角形相似,请完成下列表格:
相似比 2 k ……
周长比 ……
面积比 10000 ……
2
4
100
100
k
k2
巩固练习
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
探究新知
考点 1
利用相似三角形面积的比求面积或线段
A
B
C
D
E
F
面积为
探究新知
∴△DEF 的边 EF 上的高为 ,
∵△ABC 的边 BC 上的高为 6,面积为 ,
如果两个相似三角形的面积之比为 4 : 9,较大三角形一边上的高为 18,则较小三角形对应边上的高为______.
巩固练习
12
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
考点 2
利用相似三角形面积的比求多边形的面积(比)
探究新知
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
如图,这是圆桌正上方的灯泡 (点A ) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6(米).
∵DF∥CH,∴△ADF ∽△ACH,
巩固练习
∴ 即
解得 CH = 0.9米.
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
巩固练习
∴ 阴影部分的面积为:
A
D
E
F
C
B
H
D
返回
1.
返回
A
2.
已知两个三角形相似,若它们的对应中线之比为2:3,则它们的周长比为( )
B
返回
3.
如果两个相似三角形的对应高线的长度之比为a:b,对应的角平分线的长度之比为b:a,那么( )
A.a>b
B.a=b
C.a
4.
[2024沈阳期末]如图是学生用具三角尺ABC,∠C=90°,∠B=30°,其中△DEF∽△ABC,AB长为12 cm,DF长为3 cm,则这个三角尺中△DEF与△ABC的面积比为( )
【点拨】
【答案】B
返回
5.
【点拨】
返回
6.
5
【点拨】
相似三角形的性质
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方
课堂小结
相似三角形周长的比等于相似比
谢谢观看!
