5.4 二次函数与一元二次方程 课件(共31张PPT)
文档属性
| 名称 | 5.4 二次函数与一元二次方程 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
5.4 二次函数与一元二次方程
第5章 二次函数
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
二次函数与一元二次方程的关系
知1-讲
1
1. 二次函数图像与x轴的交点的横坐标与一元二次方程根的关系
一般地,从二次函数y=ax2+bx+c(a ≠ 0)的图像可知:如果抛物线y=ax2+bx+c(a ≠ 0)与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数值是0,因此x=x0是方程ax2+bx+c=0(a ≠ 0)的一个根.
知1-讲
2. 二次函数与一元二次方程的联系与区别
b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程ax2+bx+c=0 (a ≠ 0)的根的情况 有两个不相等的实数根x= 有两个相等的 实数根 x1=x2=- 没有实 数根
知1-讲
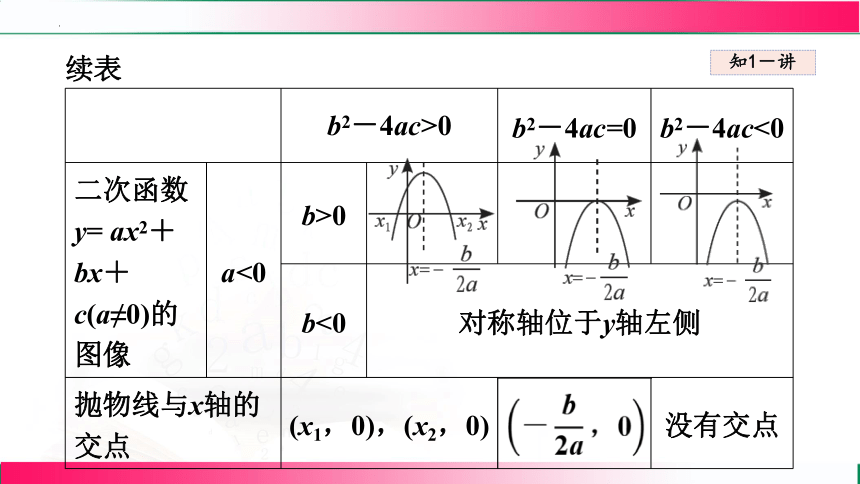
续表
b2-4ac>0 b2-4ac=0 b2-4ac<0
二次函数y= ax2+bx+c (a≠0)的图像 a>0 b<0
b>0 对称轴位于y轴左侧
知1-讲
续表
b2-4ac>0 b2-4ac=0 b2-4ac<0
二次函数y= ax2+bx+c(a≠0)的图像 a<0 b>0
b<0 对称轴位于y轴左侧 抛物线与x轴的交点 (x1,0),(x2,0) 没有交点
知1-练
例 1
[期末·北京] 已知关于x的二次函数y=mx2-4x+2的图像与x轴有公共点,则m的取值范围是 ___________.
解题秘方:紧扣抛物线与x轴的交点情况求出m的取值范围.
解:∵ y=mx2-4x+2 是二次函数,∴ m ≠ 0.
∵抛物线与x轴有交点,∴ b2-4ac ≥ 0,
即16-8m ≥ 0,解得m ≤ 2. ∴ m ≤ 2 且m ≠ 0.
m ≤ 2且m ≠ 0
知2-讲
知识点
二次函数图像与一元二次方程的近似解的关系
2
二次函数y=ax2+bx+c的图像与x轴的公共点的横坐标是一元二次方程ax2+bx+c=0 的解,因此可以借助二次函数的图像求一元二次方程的解.
(1)作出二次函数y=ax2+bx+c的图像,图像与x轴公共点的个数就是一元二次方程ax2+bx+c=0 的解的个数.
知2-讲
(2)观察图像,函数图像与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解,当函数图像与x轴有两个交点,且交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解.
知2-练
[模拟·上海] 根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a ≠ 0,a,b,c为常数)的一个解x的范围是___________.
例2
x 6.17 6.18 6.19 6.20
y=ax2+bx+c -0.03 -0.01 0.02 0.06
6.18知2-练
解题秘方:紧扣二次函数的函数值y由负变为正时,自变量x的取值即可.
解:由表格中的数据看出函数值-0.01 和0.02更接近于0,根据表格可知,当y=-0.01 时,x=6.18, 当y=0.02 时,x=6.19,故所求一个解x的范围是6.18知3-讲
知识点
二次函数y=ax2+bx+c的图像特征与a、b、c的符号关系
3
字母或式子的符号 图像的特征
a a>0 开口向上
a<0 开口向下
- b=0 对称轴为y轴
ab>0(a、b同号) 对称轴在y轴左侧
ab<0(a、b异号) 对称轴在y轴右侧
知3-讲
续表
字母或式子的符号 图像的特征
c c=0 图像过原点
c>0 图像与y轴正半轴相交
c<0 图像与y轴负半轴相交
b2-4ac b2-4ac=0 图像与x轴有唯一一个交点
b2-4ac>0 图像与x轴有两个交点
b2-4ac<0 图像与x轴没有交点
知3-讲
收藏夹
对于二次函数y=ax2+bx+c:
当x=1时,y=a+b+c,
当x=-1时,y=a-b+c,
知3-练
在平面直角坐标系中,如图5.4-2是二次函数y=ax2+
bx+c(a ≠ 0)的图像的一部分,给出下列命题:① a+b+c=0;② b>2a; ③ 方程ax2+bx+c=0 的两根分别为-3和1; ④ b2-4ac>0.
其中正确的命题有( )
A. 1 个 B. 2 个
C. 3 个 D. 4 个
例 3
返回
B
1.
二次函数y=-x2+4x-4的图像与x轴公共点的个数为( )
A.0
B.1
C.2
D.3
A
返回
2.
若二次函数y=ax2+bx+c的图像经过点(-1,0),(2,0),则关于x的方程ax2+bx+c=0的解为( )
A.x1=-1,x2=2
B.x1=-2,x2=1
C.x1=1,x2=2
D.x1=-1,x2=-2
9
返回
3.
[2023郴州]已知抛物线y=x2-6x+m与x轴有且只有
一个交点,则m=______.
-3(答案不唯一)
返回
4.
[2023泰州]二次函数y=x2+3x+n的图像与x轴有一个交点在y轴右侧,则n的值可以是__________________.(填一个值即可)
x1=-3,x2=1
返回
5.
已知二次函数y=ax2+bx+c的图像如图所示,则一元二次方程ax2+bx+c=0的解是______________.
k>-1且k≠0
返回
6.
[2024南京鼓楼区校级模拟]已知二次函数y=kx2-6x-9的图像与x轴有两个不同的交点,则k的取值范围为______________.
7.
一次函数y=x+1的图像与二次函数y=ax2+bx-3的图像交于点A(4,5),B(-1,0).
(1)确定二次函数的表达式;
(2)请在如图所示的网格中画出二次函数y=ax2+bx-3的图像;
解:如图所示.
(3)根据函数的图像直接写出方程x+1=ax2+bx-3的解.
解:x1=-1,x2=4.
返回
证明:∵(2m)2-4×(-1)×(4-m2)=
4m2+16-4m2=16>0,
∴该二次函数的图像与x轴总有两个公共点.
8.
[2024南京玄武区二模]已知二次函数y=-x2+2mx+4-m2(m为常数).
(1)求证:该二次函数的图像与x轴总有两个公共点;
(2)设该函数图像的顶点为C,与x轴交于A,B两点,与y轴交于点D,当△ABC的面积与△ABD的面积相等时,求m的值.
返回
返回
A
9.
[2024南京栖霞区开学测试]如图是二次函数y=ax2+bx+c的图像,若关于x的方程ax2+bx+c=m总有一正一负两个实数根,则m的取值范围是( )
A.m>3 B.m<3
C.m≥3 D.m≤3
返回
A
10.
[2024泸州]已知二次函数y=ax2+(2a-3)x+a-1(x是自变量)的图像经过第一、二、四象限,则实数a的取值范围为( )
返回
B
11.
[2024扬州广陵区一模]小明研究二次函数y=(x-m)2+m-1(m为常数)的性质时,得出如下结论:①这个函数图像的顶点始终在直线y=x-1上;②存在两个m的值,使得函数图像的顶点和图像与x轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图像上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<3时,y随x的增大而减小,则m的取值范围为m≥3.其中错误结论的序号是( )
A.① B.② C.③ D.④
二次函数与一元二次方程
二次函数
与一元二
次方程之
间的关系
二次函数图像与x轴的公共点个数
有两个公共点
有一个公共点
没有公共点
有两个不相
等的实数根
有两个相等
的实数根
没有实数根
一元二次方程根的个数
谢谢观看!
5.4 二次函数与一元二次方程
第5章 二次函数
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
二次函数与一元二次方程的关系
知1-讲
1
1. 二次函数图像与x轴的交点的横坐标与一元二次方程根的关系
一般地,从二次函数y=ax2+bx+c(a ≠ 0)的图像可知:如果抛物线y=ax2+bx+c(a ≠ 0)与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数值是0,因此x=x0是方程ax2+bx+c=0(a ≠ 0)的一个根.
知1-讲
2. 二次函数与一元二次方程的联系与区别
b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程ax2+bx+c=0 (a ≠ 0)的根的情况 有两个不相等的实数根x= 有两个相等的 实数根 x1=x2=- 没有实 数根
知1-讲
续表
b2-4ac>0 b2-4ac=0 b2-4ac<0
二次函数y= ax2+bx+c (a≠0)的图像 a>0 b<0
b>0 对称轴位于y轴左侧
知1-讲
续表
b2-4ac>0 b2-4ac=0 b2-4ac<0
二次函数y= ax2+bx+c(a≠0)的图像 a<0 b>0
b<0 对称轴位于y轴左侧 抛物线与x轴的交点 (x1,0),(x2,0) 没有交点
知1-练
例 1
[期末·北京] 已知关于x的二次函数y=mx2-4x+2的图像与x轴有公共点,则m的取值范围是 ___________.
解题秘方:紧扣抛物线与x轴的交点情况求出m的取值范围.
解:∵ y=mx2-4x+2 是二次函数,∴ m ≠ 0.
∵抛物线与x轴有交点,∴ b2-4ac ≥ 0,
即16-8m ≥ 0,解得m ≤ 2. ∴ m ≤ 2 且m ≠ 0.
m ≤ 2且m ≠ 0
知2-讲
知识点
二次函数图像与一元二次方程的近似解的关系
2
二次函数y=ax2+bx+c的图像与x轴的公共点的横坐标是一元二次方程ax2+bx+c=0 的解,因此可以借助二次函数的图像求一元二次方程的解.
(1)作出二次函数y=ax2+bx+c的图像,图像与x轴公共点的个数就是一元二次方程ax2+bx+c=0 的解的个数.
知2-讲
(2)观察图像,函数图像与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解,当函数图像与x轴有两个交点,且交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解.
知2-练
[模拟·上海] 根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a ≠ 0,a,b,c为常数)的一个解x的范围是___________.
例2
x 6.17 6.18 6.19 6.20
y=ax2+bx+c -0.03 -0.01 0.02 0.06
6.18
解题秘方:紧扣二次函数的函数值y由负变为正时,自变量x的取值即可.
解:由表格中的数据看出函数值-0.01 和0.02更接近于0,根据表格可知,当y=-0.01 时,x=6.18, 当y=0.02 时,x=6.19,故所求一个解x的范围是6.18
知识点
二次函数y=ax2+bx+c的图像特征与a、b、c的符号关系
3
字母或式子的符号 图像的特征
a a>0 开口向上
a<0 开口向下
- b=0 对称轴为y轴
ab>0(a、b同号) 对称轴在y轴左侧
ab<0(a、b异号) 对称轴在y轴右侧
知3-讲
续表
字母或式子的符号 图像的特征
c c=0 图像过原点
c>0 图像与y轴正半轴相交
c<0 图像与y轴负半轴相交
b2-4ac b2-4ac=0 图像与x轴有唯一一个交点
b2-4ac>0 图像与x轴有两个交点
b2-4ac<0 图像与x轴没有交点
知3-讲
收藏夹
对于二次函数y=ax2+bx+c:
当x=1时,y=a+b+c,
当x=-1时,y=a-b+c,
知3-练
在平面直角坐标系中,如图5.4-2是二次函数y=ax2+
bx+c(a ≠ 0)的图像的一部分,给出下列命题:① a+b+c=0;② b>2a; ③ 方程ax2+bx+c=0 的两根分别为-3和1; ④ b2-4ac>0.
其中正确的命题有( )
A. 1 个 B. 2 个
C. 3 个 D. 4 个
例 3
返回
B
1.
二次函数y=-x2+4x-4的图像与x轴公共点的个数为( )
A.0
B.1
C.2
D.3
A
返回
2.
若二次函数y=ax2+bx+c的图像经过点(-1,0),(2,0),则关于x的方程ax2+bx+c=0的解为( )
A.x1=-1,x2=2
B.x1=-2,x2=1
C.x1=1,x2=2
D.x1=-1,x2=-2
9
返回
3.
[2023郴州]已知抛物线y=x2-6x+m与x轴有且只有
一个交点,则m=______.
-3(答案不唯一)
返回
4.
[2023泰州]二次函数y=x2+3x+n的图像与x轴有一个交点在y轴右侧,则n的值可以是__________________.(填一个值即可)
x1=-3,x2=1
返回
5.
已知二次函数y=ax2+bx+c的图像如图所示,则一元二次方程ax2+bx+c=0的解是______________.
k>-1且k≠0
返回
6.
[2024南京鼓楼区校级模拟]已知二次函数y=kx2-6x-9的图像与x轴有两个不同的交点,则k的取值范围为______________.
7.
一次函数y=x+1的图像与二次函数y=ax2+bx-3的图像交于点A(4,5),B(-1,0).
(1)确定二次函数的表达式;
(2)请在如图所示的网格中画出二次函数y=ax2+bx-3的图像;
解:如图所示.
(3)根据函数的图像直接写出方程x+1=ax2+bx-3的解.
解:x1=-1,x2=4.
返回
证明:∵(2m)2-4×(-1)×(4-m2)=
4m2+16-4m2=16>0,
∴该二次函数的图像与x轴总有两个公共点.
8.
[2024南京玄武区二模]已知二次函数y=-x2+2mx+4-m2(m为常数).
(1)求证:该二次函数的图像与x轴总有两个公共点;
(2)设该函数图像的顶点为C,与x轴交于A,B两点,与y轴交于点D,当△ABC的面积与△ABD的面积相等时,求m的值.
返回
返回
A
9.
[2024南京栖霞区开学测试]如图是二次函数y=ax2+bx+c的图像,若关于x的方程ax2+bx+c=m总有一正一负两个实数根,则m的取值范围是( )
A.m>3 B.m<3
C.m≥3 D.m≤3
返回
A
10.
[2024泸州]已知二次函数y=ax2+(2a-3)x+a-1(x是自变量)的图像经过第一、二、四象限,则实数a的取值范围为( )
返回
B
11.
[2024扬州广陵区一模]小明研究二次函数y=(x-m)2+m-1(m为常数)的性质时,得出如下结论:①这个函数图像的顶点始终在直线y=x-1上;②存在两个m的值,使得函数图像的顶点和图像与x轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图像上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<3时,y随x的增大而减小,则m的取值范围为m≥3.其中错误结论的序号是( )
A.① B.② C.③ D.④
二次函数与一元二次方程
二次函数
与一元二
次方程之
间的关系
二次函数图像与x轴的公共点个数
有两个公共点
有一个公共点
没有公共点
有两个不相
等的实数根
有两个相等
的实数根
没有实数根
一元二次方程根的个数
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
