6.3 相似图形 课件(共32张PPT)
文档属性
| 名称 | 6.3 相似图形 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 16:27:56 | ||
图片预览









文档简介
(共32张PPT)
6.3 相似图形
第6章 图形的相似
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 情境导入(5 分钟)
问题 1:展示两张大小不同但形状相同的照片(如同一风景的原图与缩略图),提问:
“这两张照片有什么共同点和不同点?”
问题 2:展示地图与实际地形的关系,提问:
“地图上的距离与实际距离有什么联系?”
引出课题:图形的相似。
2. 探究新知(20 分钟)
活动 1:观察与分类
展示几组图形(如等边三角形、正方形、长方形、任意五边形等),引导学生分类并讨论:
“哪些图形形状相同但大小不同?”
归纳定义:形状相同的图形称为相似图形(similar figures)。
强调:相似图形的大小不一定相同,但形状必须完全相同。
活动 2:相似多边形的性质
以两个相似三角形为例,引导学生测量对应角和对应边的比例。
结论:相似多边形的对应角相等,对应边成比例。
相似比:对应边的比值称为相似比(similarity ratio)。
活动 3:判定相似多边形
反例分析:展示两个边成比例但角不相等的多边形,提问:
“它们是否相似?为什么?”
总结:相似多边形必须同时满足对应角相等和对应边成比例。
3. 例题解析(10 分钟)
例题 1:已知四边形 ABCD∽四边形 A’B’C’D’,AB=4,A’B’=6,∠A=80°,求相似比及∠A’的度数。
分析:相似比 = AB:A’B’=4:6=2:3;对应角∠A’=∠A=80°。
例题 2:判断两个矩形是否相似,已知矩形甲边长为 3 和 6,矩形乙边长为 4 和 8。
分析:对应边比例均为 1:2,对应角均为 90°,因此相似。
4. 巩固练习(10 分钟)
练习 1:教材习题(判断图形是否相似,计算相似比)。
练习 2:小组合作设计两个相似多边形,并说明理由。
5. 课堂小结(5 分钟)
学生总结:相似图形的定义、相似多边形的性质。
教师补充:相似比的意义及判定方法。
四、作业布置
基础题:教材课后习题(必做)。
拓展题:测量家中两个相似物体(如书本与练习本)的边长,计算相似比。
思考题:相似图形与全等图形的关系是什么?
五、教学资源
多媒体课件(含几何画板动态演示)。
实物投影仪展示学生作品。
六、教学反思
通过生活实例降低抽象概念的理解难度。
需关注学生对 “对应角”“对应边” 的理解是否到位,避免比例计算错误。
教案设计说明:
结合直观观察与数学推理,帮助学生从感性认识过渡到理性认识。
注重知识的实际应用,培养学生用数学解决问题的能力。
知识点
相似形
知1-讲
1
1. 定义 形状相同的图形叫做相似形.
2. 两个关系
(1)相似图形之间的关系:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
知1-讲
(2)相似与全等的关系:当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
知1-练
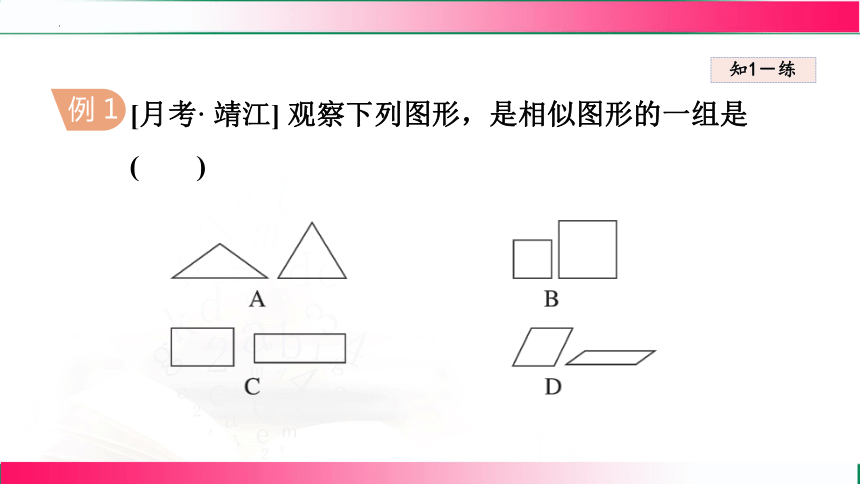
例 1
[月考· 靖江] 观察下列图形,是相似图形的一组是( )
知2-讲
知识点
相似多边形
2
1. 相似多边形的定义 各角分别相等、各边成比例的两个多边形,它们的形状相同,称为相似多边形.
2. 相似比的定义 相似多边形的对应边的比叫做相似比.
3. 相似多边形的性质 相似多边形的对应角相等,对应边成比例.
知2-讲
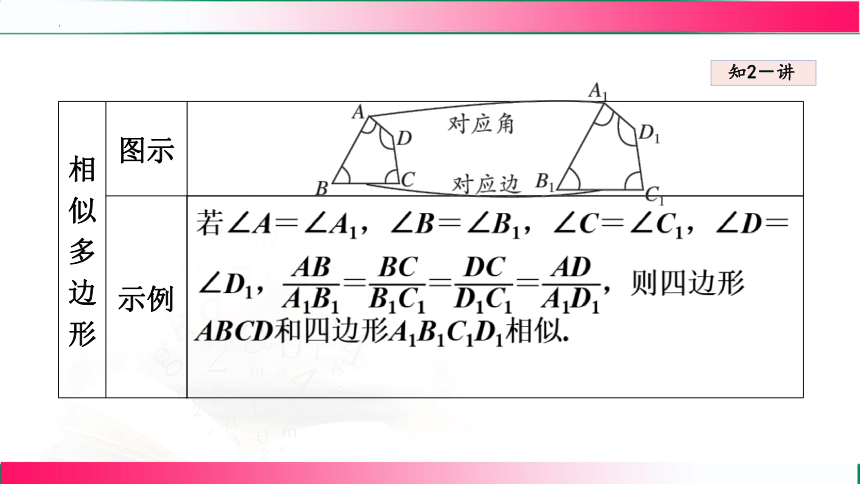
相似多边形 图示
示例 若∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,===,则四边形ABCD和四边形A1B1C1D1相似.
知2-讲
相似多边形 记法 “四边形ABCD与四边形A1B1C1D1相似”记作“四边形ABCD∽四边形A1B1C1D1”.
读法 四边形ABCD相似于四边形A1B1C1D1.
续表
知2-讲
要点提醒
1. 判定相似多边形的条件:
①所有的角分别对应相等;
②所有的边对应成比例.
2. 相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
3. 相似比与两个多边形的先后顺序有关.
知2-练
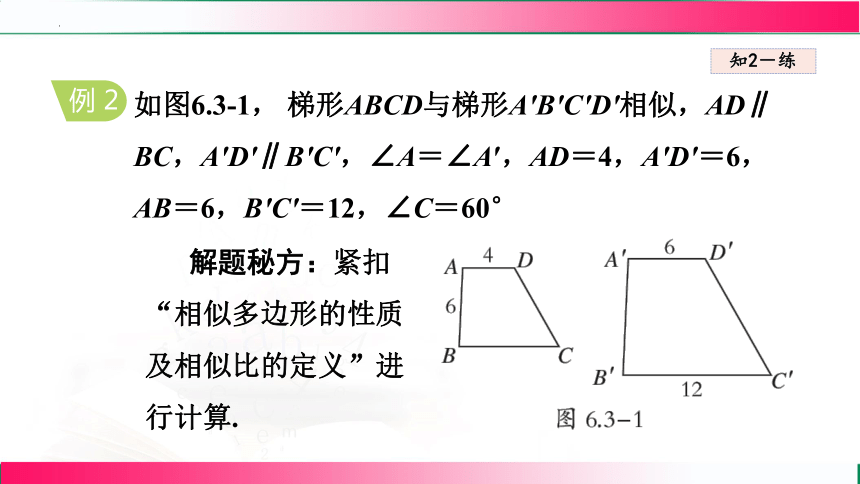
如图6.3-1, 梯形ABCD与梯形A′B′C′D′相似,AD∥ BC,A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°
例 2
解题秘方:紧扣“相似多边形的性质及相似比的定义”进行计算.
知2-练
(1)求梯形ABCD与梯形A′B′C′D′的相似比k;
解:k===.
知2-练
(2)求A′B′和BC的长;
解:∵梯形ABCD与梯形A′B ′C′D′相似,且由(1)知相似比k=,∴ =,=.
又∵ AB=6,B′C′=12,∴ A′B′=9,BC=8.
知2-练
(3)求∠D′的大小.
解:∵ AD∥BC,∠C=60°,
∴∠D=180°-∠C=120°.
由题意知∠D′=∠D,∴∠D′=120°.
知3-讲
知识点
相似三角形
3
1. 相似三角形的定义 各角分别相等、各边成比例的两个三角形称为相似三角形.
知3-讲
2. 特别解读
(1)相似用符号“∽”表示,记两个三角形相似时,应把对应顶点的字母写在对应的位置上. 如图6.3-2,△ABC相似于△A′B′C′,记作△ABC∽△A′B′C′,对应边的比,如叫做相似比.
知3-讲
(2)相似比是有顺序的. 如图6.3-2,△ABC∽△A′B′C′,它们的相似比是===k,如果写成△A′B′C′∽△ABC,那么它们的相似比为===k′,因此k=.
(3)全等用符号“≌”表示,
对应边相等,此时相似比 “k=1”.
知3-讲
要点提醒
1. 判断两个三角形相似的条件:
(1)三角形的三组角分别对应相等;
(2)三角形的三组边对应成比例.
2. 相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
3. 在相似多边形中,最简单的就是相似三角形.
知3-练
[期末·无锡] 如图6.3-3,AB∥CD,AD、BC相交于点O,AB=6,CD=9,AD=10,OD=6,BO=3,OC=4.5,求证:△ABO∽△DCO.
例 3
解题秘方:紧扣相似三角形的定义列出相似的条件求解.
知3-练
证明:∵ AD=10,OD=6,∴ AO=4.
∵==,==,==,
∴ = =.
∵ AB∥CD,∴∠B=∠C,∠A=∠D.
又∵∠AOB=∠DOC,∴△ABO∽△DCO.
知3-练
如果△ABO∽△DCO,则==就是两个三角形的相似比,即k=.
返回
D
1.
下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
B
返回
2.
[2024无锡梁溪区期末]如图,若△ADC∽△BAC,则下列结论错误的是( )
C
返回
3.
四边形ABCD的边长分别为2,3,4,5,和它相似的
四边形A1B1C1D1的最长边长为15,则四边形A1B1C1D1的最短边长为( )
A.2 B.4
C.6 D.8
48°
返回
4.
如图,四边形ABCD∽四边形A′B′C′D′,则∠D′的度数为________.
返回
5.
[2024泰州高港区期末]如图,矩形ABCD被分割为3个面积相等的小矩形,已知矩形AFED与原矩形ABCD相似,则原矩形的较长边与较短边的比值是________.
返回
6.
[2024东台期中]如图,已知四边形AEFD∽四边形EBCF,若AD=3,EF=4,则BC的长为________.
7.
如图,把一个矩形ABCD划分成三个全等的小矩形.
(1)若原矩形ABCD的长AB=6,宽BC=4.问:每个小矩形与原矩形相似吗?请说明理由.
(2)若原矩形的长AB=a,宽BC=b,且每个小矩形与原矩形相似,求a与b应满足的关系式.
返回
C
返回
8.
[2024常州武进区期末]如图,四边形ABCD是一张矩形纸片.折叠该矩形纸片,使AB边落在AD边上,点B的对应点为点F,折痕为AE,展平后连接EF;继续折叠该纸片,使FD落在FE上,点D的对应点为点H,折痕为FG,展平后连接HG.
若矩形HECG∽矩形ABCD,
AD=1,则CD的长为( )
相似图形
相似
图形
相似三角
形的定义
相似三角
形的性质
相似多边
形的定义
相似多边形
的性质
谢谢观看!
6.3 相似图形
第6章 图形的相似
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 情境导入(5 分钟)
问题 1:展示两张大小不同但形状相同的照片(如同一风景的原图与缩略图),提问:
“这两张照片有什么共同点和不同点?”
问题 2:展示地图与实际地形的关系,提问:
“地图上的距离与实际距离有什么联系?”
引出课题:图形的相似。
2. 探究新知(20 分钟)
活动 1:观察与分类
展示几组图形(如等边三角形、正方形、长方形、任意五边形等),引导学生分类并讨论:
“哪些图形形状相同但大小不同?”
归纳定义:形状相同的图形称为相似图形(similar figures)。
强调:相似图形的大小不一定相同,但形状必须完全相同。
活动 2:相似多边形的性质
以两个相似三角形为例,引导学生测量对应角和对应边的比例。
结论:相似多边形的对应角相等,对应边成比例。
相似比:对应边的比值称为相似比(similarity ratio)。
活动 3:判定相似多边形
反例分析:展示两个边成比例但角不相等的多边形,提问:
“它们是否相似?为什么?”
总结:相似多边形必须同时满足对应角相等和对应边成比例。
3. 例题解析(10 分钟)
例题 1:已知四边形 ABCD∽四边形 A’B’C’D’,AB=4,A’B’=6,∠A=80°,求相似比及∠A’的度数。
分析:相似比 = AB:A’B’=4:6=2:3;对应角∠A’=∠A=80°。
例题 2:判断两个矩形是否相似,已知矩形甲边长为 3 和 6,矩形乙边长为 4 和 8。
分析:对应边比例均为 1:2,对应角均为 90°,因此相似。
4. 巩固练习(10 分钟)
练习 1:教材习题(判断图形是否相似,计算相似比)。
练习 2:小组合作设计两个相似多边形,并说明理由。
5. 课堂小结(5 分钟)
学生总结:相似图形的定义、相似多边形的性质。
教师补充:相似比的意义及判定方法。
四、作业布置
基础题:教材课后习题(必做)。
拓展题:测量家中两个相似物体(如书本与练习本)的边长,计算相似比。
思考题:相似图形与全等图形的关系是什么?
五、教学资源
多媒体课件(含几何画板动态演示)。
实物投影仪展示学生作品。
六、教学反思
通过生活实例降低抽象概念的理解难度。
需关注学生对 “对应角”“对应边” 的理解是否到位,避免比例计算错误。
教案设计说明:
结合直观观察与数学推理,帮助学生从感性认识过渡到理性认识。
注重知识的实际应用,培养学生用数学解决问题的能力。
知识点
相似形
知1-讲
1
1. 定义 形状相同的图形叫做相似形.
2. 两个关系
(1)相似图形之间的关系:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
知1-讲
(2)相似与全等的关系:当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
知1-练
例 1
[月考· 靖江] 观察下列图形,是相似图形的一组是( )
知2-讲
知识点
相似多边形
2
1. 相似多边形的定义 各角分别相等、各边成比例的两个多边形,它们的形状相同,称为相似多边形.
2. 相似比的定义 相似多边形的对应边的比叫做相似比.
3. 相似多边形的性质 相似多边形的对应角相等,对应边成比例.
知2-讲
相似多边形 图示
示例 若∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,===,则四边形ABCD和四边形A1B1C1D1相似.
知2-讲
相似多边形 记法 “四边形ABCD与四边形A1B1C1D1相似”记作“四边形ABCD∽四边形A1B1C1D1”.
读法 四边形ABCD相似于四边形A1B1C1D1.
续表
知2-讲
要点提醒
1. 判定相似多边形的条件:
①所有的角分别对应相等;
②所有的边对应成比例.
2. 相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
3. 相似比与两个多边形的先后顺序有关.
知2-练
如图6.3-1, 梯形ABCD与梯形A′B′C′D′相似,AD∥ BC,A′D′∥B′C′,∠A=∠A′,AD=4,A′D′=6,AB=6,B′C′=12,∠C=60°
例 2
解题秘方:紧扣“相似多边形的性质及相似比的定义”进行计算.
知2-练
(1)求梯形ABCD与梯形A′B′C′D′的相似比k;
解:k===.
知2-练
(2)求A′B′和BC的长;
解:∵梯形ABCD与梯形A′B ′C′D′相似,且由(1)知相似比k=,∴ =,=.
又∵ AB=6,B′C′=12,∴ A′B′=9,BC=8.
知2-练
(3)求∠D′的大小.
解:∵ AD∥BC,∠C=60°,
∴∠D=180°-∠C=120°.
由题意知∠D′=∠D,∴∠D′=120°.
知3-讲
知识点
相似三角形
3
1. 相似三角形的定义 各角分别相等、各边成比例的两个三角形称为相似三角形.
知3-讲
2. 特别解读
(1)相似用符号“∽”表示,记两个三角形相似时,应把对应顶点的字母写在对应的位置上. 如图6.3-2,△ABC相似于△A′B′C′,记作△ABC∽△A′B′C′,对应边的比,如叫做相似比.
知3-讲
(2)相似比是有顺序的. 如图6.3-2,△ABC∽△A′B′C′,它们的相似比是===k,如果写成△A′B′C′∽△ABC,那么它们的相似比为===k′,因此k=.
(3)全等用符号“≌”表示,
对应边相等,此时相似比 “k=1”.
知3-讲
要点提醒
1. 判断两个三角形相似的条件:
(1)三角形的三组角分别对应相等;
(2)三角形的三组边对应成比例.
2. 相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
3. 在相似多边形中,最简单的就是相似三角形.
知3-练
[期末·无锡] 如图6.3-3,AB∥CD,AD、BC相交于点O,AB=6,CD=9,AD=10,OD=6,BO=3,OC=4.5,求证:△ABO∽△DCO.
例 3
解题秘方:紧扣相似三角形的定义列出相似的条件求解.
知3-练
证明:∵ AD=10,OD=6,∴ AO=4.
∵==,==,==,
∴ = =.
∵ AB∥CD,∴∠B=∠C,∠A=∠D.
又∵∠AOB=∠DOC,∴△ABO∽△DCO.
知3-练
如果△ABO∽△DCO,则==就是两个三角形的相似比,即k=.
返回
D
1.
下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为( )
A.甲和乙 B.乙和丁 C.甲和丙 D.甲和丁
B
返回
2.
[2024无锡梁溪区期末]如图,若△ADC∽△BAC,则下列结论错误的是( )
C
返回
3.
四边形ABCD的边长分别为2,3,4,5,和它相似的
四边形A1B1C1D1的最长边长为15,则四边形A1B1C1D1的最短边长为( )
A.2 B.4
C.6 D.8
48°
返回
4.
如图,四边形ABCD∽四边形A′B′C′D′,则∠D′的度数为________.
返回
5.
[2024泰州高港区期末]如图,矩形ABCD被分割为3个面积相等的小矩形,已知矩形AFED与原矩形ABCD相似,则原矩形的较长边与较短边的比值是________.
返回
6.
[2024东台期中]如图,已知四边形AEFD∽四边形EBCF,若AD=3,EF=4,则BC的长为________.
7.
如图,把一个矩形ABCD划分成三个全等的小矩形.
(1)若原矩形ABCD的长AB=6,宽BC=4.问:每个小矩形与原矩形相似吗?请说明理由.
(2)若原矩形的长AB=a,宽BC=b,且每个小矩形与原矩形相似,求a与b应满足的关系式.
返回
C
返回
8.
[2024常州武进区期末]如图,四边形ABCD是一张矩形纸片.折叠该矩形纸片,使AB边落在AD边上,点B的对应点为点F,折痕为AE,展平后连接EF;继续折叠该纸片,使FD落在FE上,点D的对应点为点H,折痕为FG,展平后连接HG.
若矩形HECG∽矩形ABCD,
AD=1,则CD的长为( )
相似图形
相似
图形
相似三角
形的定义
相似三角
形的性质
相似多边
形的定义
相似多边形
的性质
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
