6.4.1 平行线分线段成比例 课件(共20张PPT)
文档属性
| 名称 | 6.4.1 平行线分线段成比例 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 16:28:35 | ||
图片预览







文档简介
(共20张PPT)
6.4.1 平行线分线段成比例
第6章 图形的相似
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
1. 情境导入(5 分钟)
问题 1:展示两张大小不同但形状相同的照片(如同一风景的原图与缩略图),提问:
“这两张照片有什么共同点和不同点?”
问题 2:展示地图与实际地形的关系,提问:
“地图上的距离与实际距离有什么联系?”
引出课题:图形的相似。
2. 探究新知(20 分钟)
活动 1:观察与分类
展示几组图形(如等边三角形、正方形、长方形、任意五边形等),引导学生分类并讨论:
“哪些图形形状相同但大小不同?”
归纳定义:形状相同的图形称为相似图形(similar figures)。
强调:相似图形的大小不一定相同,但形状必须完全相同。
活动 2:相似多边形的性质
以两个相似三角形为例,引导学生测量对应角和对应边的比例。
结论:相似多边形的对应角相等,对应边成比例。
相似比:对应边的比值称为相似比(similarity ratio)。
活动 3:判定相似多边形
反例分析:展示两个边成比例但角不相等的多边形,提问:
“它们是否相似?为什么?”
总结:相似多边形必须同时满足对应角相等和对应边成比例。
3. 例题解析(10 分钟)
例题 1:已知四边形 ABCD∽四边形 A’B’C’D’,AB=4,A’B’=6,∠A=80°,求相似比及∠A’的度数。
分析:相似比 = AB:A’B’=4:6=2:3;对应角∠A’=∠A=80°。
例题 2:判断两个矩形是否相似,已知矩形甲边长为 3 和 6,矩形乙边长为 4 和 8。
分析:对应边比例均为 1:2,对应角均为 90°,因此相似。
4. 巩固练习(10 分钟)
练习 1:教材习题(判断图形是否相似,计算相似比)。
练习 2:小组合作设计两个相似多边形,并说明理由。
5. 课堂小结(5 分钟)
学生总结:相似图形的定义、相似多边形的性质。
教师补充:相似比的意义及判定方法。
四、作业布置
基础题:教材课后习题(必做)。
拓展题:测量家中两个相似物体(如书本与练习本)的边长,计算相似比。
思考题:相似图形与全等图形的关系是什么?
五、教学资源
多媒体课件(含几何画板动态演示)。
实物投影仪展示学生作品。
六、教学反思
通过生活实例降低抽象概念的理解难度。
需关注学生对 “对应角”“对应边” 的理解是否到位,避免比例计算错误。
教案设计说明:
结合直观观察与数学推理,帮助学生从感性认识过渡到理性认识。
注重知识的实际应用,培养学生用数学解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
平行线分线段成比例
知1-讲
1
1. 平行线分线段成比例的基本事实 两条直线
被一组平行线所截,所得的对应线段成比例.
符号语言: 如图6.4-1 所示,
∵ l3∥l4∥l5,∴=,=,= .
可简记为:=,=,=.
平行线分线段成比例
知1-讲
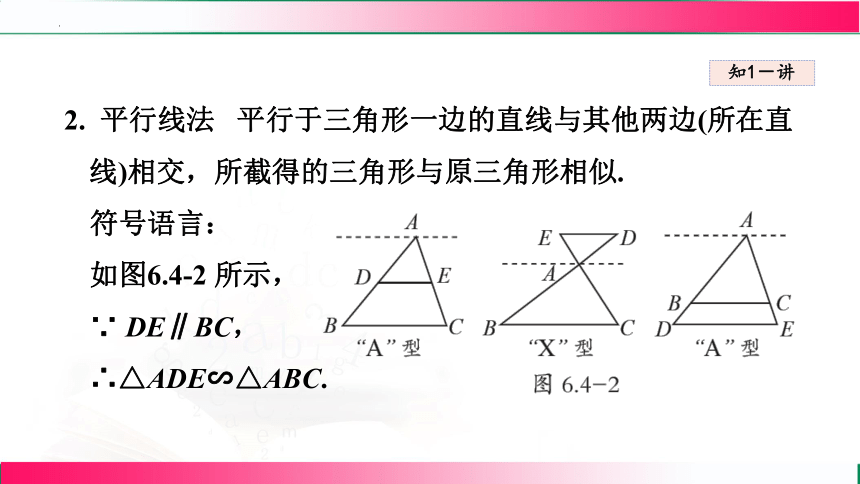
2. 平行线法 平行于三角形一边的直线与其他两边(所在直线)相交,所截得的三角形与原三角形相似.
符号语言:
如图6.4-2 所示,
∵ DE∥BC,
∴△ADE∽△ABC.
知1-讲
要点解读
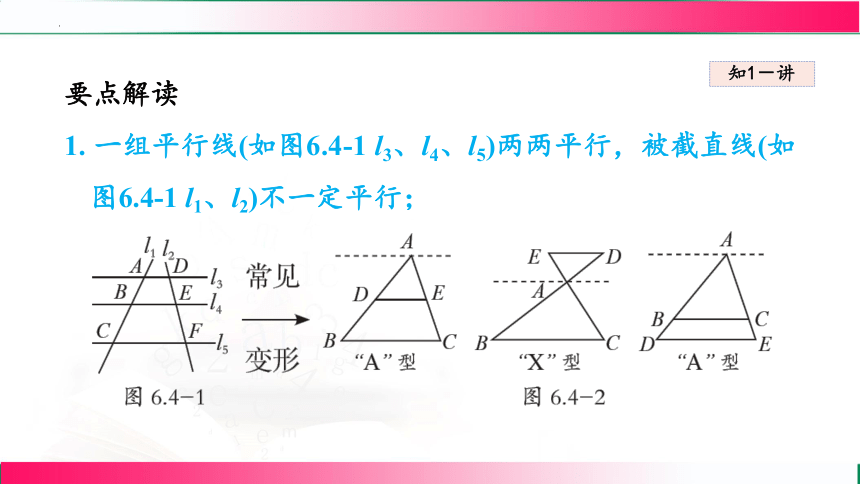
1. 一组平行线(如图6.4-1 l3、l4、l5)两两平行,被截直线(如图6.4-1 l1、l2)不一定平行;
知1-讲
2. 所有的成比例线段是指被截直线上的线段,与这组平行线上的线段无关;
3. 利用平行线分线段成比例的基本事实写比例式时,一定要注意对应线段写在对应的位置上.
知1-练
例 1
[一模· 淮安] 如图6.4-3, 已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,
且AB=3,BC=4,EF=4.8,则DE的长为______.
3.6
知1-练
解题秘方:利用平行线分线段成比例的基本事实解决问题即可.
解:∵ a∥b∥c,∴=(两条直线被一组平行线所截,所得的对应线段成比例).
∵ AB=3,BC=4,EF=4.8,
∴=,解得DE=3.6.
知1-练
解法提醒
在题目中,遇到与直线平行相关的问题时,可从两个方面获取信息:
一是角之间的关系(同位角相等、内错角相等、同旁内角互补);
二是线段之间的关系,即平行线分线段成比例.
返回
A
1.
A
返回
2.
[2024扬州广陵区校级期中]如图,已知AB∥CD∥EF,那么下列结论正确的是( )
4 cm
返回
3.
返回
4.
如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC=________.
返回
5.
[2024扬州仪征校级月考]如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
6.
[2024苏州姑苏区校级月考]如图,在△ABC中,D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
返回
C
返回
7.
[2024宿迁沭阳模拟]如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于点E,若BE=1,则EC的长为( )
A.2 B.2.5
C.3 D.4
5
返回
8.
9.
谢谢观看!
6.4.1 平行线分线段成比例
第6章 图形的相似
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
1. 情境导入(5 分钟)
问题 1:展示两张大小不同但形状相同的照片(如同一风景的原图与缩略图),提问:
“这两张照片有什么共同点和不同点?”
问题 2:展示地图与实际地形的关系,提问:
“地图上的距离与实际距离有什么联系?”
引出课题:图形的相似。
2. 探究新知(20 分钟)
活动 1:观察与分类
展示几组图形(如等边三角形、正方形、长方形、任意五边形等),引导学生分类并讨论:
“哪些图形形状相同但大小不同?”
归纳定义:形状相同的图形称为相似图形(similar figures)。
强调:相似图形的大小不一定相同,但形状必须完全相同。
活动 2:相似多边形的性质
以两个相似三角形为例,引导学生测量对应角和对应边的比例。
结论:相似多边形的对应角相等,对应边成比例。
相似比:对应边的比值称为相似比(similarity ratio)。
活动 3:判定相似多边形
反例分析:展示两个边成比例但角不相等的多边形,提问:
“它们是否相似?为什么?”
总结:相似多边形必须同时满足对应角相等和对应边成比例。
3. 例题解析(10 分钟)
例题 1:已知四边形 ABCD∽四边形 A’B’C’D’,AB=4,A’B’=6,∠A=80°,求相似比及∠A’的度数。
分析:相似比 = AB:A’B’=4:6=2:3;对应角∠A’=∠A=80°。
例题 2:判断两个矩形是否相似,已知矩形甲边长为 3 和 6,矩形乙边长为 4 和 8。
分析:对应边比例均为 1:2,对应角均为 90°,因此相似。
4. 巩固练习(10 分钟)
练习 1:教材习题(判断图形是否相似,计算相似比)。
练习 2:小组合作设计两个相似多边形,并说明理由。
5. 课堂小结(5 分钟)
学生总结:相似图形的定义、相似多边形的性质。
教师补充:相似比的意义及判定方法。
四、作业布置
基础题:教材课后习题(必做)。
拓展题:测量家中两个相似物体(如书本与练习本)的边长,计算相似比。
思考题:相似图形与全等图形的关系是什么?
五、教学资源
多媒体课件(含几何画板动态演示)。
实物投影仪展示学生作品。
六、教学反思
通过生活实例降低抽象概念的理解难度。
需关注学生对 “对应角”“对应边” 的理解是否到位,避免比例计算错误。
教案设计说明:
结合直观观察与数学推理,帮助学生从感性认识过渡到理性认识。
注重知识的实际应用,培养学生用数学解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
平行线分线段成比例
知1-讲
1
1. 平行线分线段成比例的基本事实 两条直线
被一组平行线所截,所得的对应线段成比例.
符号语言: 如图6.4-1 所示,
∵ l3∥l4∥l5,∴=,=,= .
可简记为:=,=,=.
平行线分线段成比例
知1-讲
2. 平行线法 平行于三角形一边的直线与其他两边(所在直线)相交,所截得的三角形与原三角形相似.
符号语言:
如图6.4-2 所示,
∵ DE∥BC,
∴△ADE∽△ABC.
知1-讲
要点解读
1. 一组平行线(如图6.4-1 l3、l4、l5)两两平行,被截直线(如图6.4-1 l1、l2)不一定平行;
知1-讲
2. 所有的成比例线段是指被截直线上的线段,与这组平行线上的线段无关;
3. 利用平行线分线段成比例的基本事实写比例式时,一定要注意对应线段写在对应的位置上.
知1-练
例 1
[一模· 淮安] 如图6.4-3, 已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,
且AB=3,BC=4,EF=4.8,则DE的长为______.
3.6
知1-练
解题秘方:利用平行线分线段成比例的基本事实解决问题即可.
解:∵ a∥b∥c,∴=(两条直线被一组平行线所截,所得的对应线段成比例).
∵ AB=3,BC=4,EF=4.8,
∴=,解得DE=3.6.
知1-练
解法提醒
在题目中,遇到与直线平行相关的问题时,可从两个方面获取信息:
一是角之间的关系(同位角相等、内错角相等、同旁内角互补);
二是线段之间的关系,即平行线分线段成比例.
返回
A
1.
A
返回
2.
[2024扬州广陵区校级期中]如图,已知AB∥CD∥EF,那么下列结论正确的是( )
4 cm
返回
3.
返回
4.
如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC=________.
返回
5.
[2024扬州仪征校级月考]如图,在△ABC中,EF∥CD,DE∥BC.求证:AF:FD=AD:DB.
6.
[2024苏州姑苏区校级月考]如图,在△ABC中,D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.
返回
C
返回
7.
[2024宿迁沭阳模拟]如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于点E,若BE=1,则EC的长为( )
A.2 B.2.5
C.3 D.4
5
返回
8.
9.
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
