7.1 正切 课件(共28张PPT)

(共28张PPT)
7.1正切
第7章 锐角三角函数
苏科版数学九年级下册【示范课精品课件】
授课教师：********
班 级：********
时 间：********
在黑板上画出一个直角三角形 ABC，其中∠C = 90°。设∠A、∠B、∠C 所对的边分别为 a、b、c。
正弦函数定义
引导学生观察∠A 的对边 a 与斜边 c 的比值，给出正弦函数的定义：在 Rt△ABC 中，锐角 A 的对边与斜边的比叫做∠A 的正弦，记作 sinA，即 sinA = a/c 。通过多个不同边长的直角三角形示例，让学生计算∠A 的正弦值，加深对定义的理解。
余弦函数定义
类比正弦函数，讲解余弦函数：锐角 A 的邻边 b 与斜边 c 的比叫做∠A 的余弦，记作 cosA，即 cosA = b/c 。同样通过实例计算强化概念。
正切函数定义
介绍正切函数：锐角 A 的对边 a 与邻边 b 的比叫做∠A 的正切，记作 tanA，即 tanA = a/b 。引导学生分析正切函数与正弦、余弦函数的区别与联系。
（三）例题讲解（15 分钟）
例 1：在 Rt△ABC 中，∠C = 90°，a = 3，b = 4，求 sinA、cosA、tanA 的值。
分析：首先根据勾股定理求出斜边 c 的值，然后根据正弦、余弦、正切函数的定义分别计算。
解：由勾股定理得 c = √(a + b ) = √(3 + 4 ) = 5
sinA = a/c = 3/5
cosA = b/c = 4/5
tanA = a/b = 3/4
例 2：在 Rt△ABC 中，∠C = 90°，sinA = 3/5 ，a = 6，求 b 和 c 的值。
分析：根据正弦函数定义先求出 c 的值，再利用勾股定理求出 b 的值。
解：因为 sinA = a/c = 3/5 ，a = 6，所以 c = a÷(3/5) = 6×(5/3) = 10
由勾股定理得 b = √(c - a ) = √(10 - 6 ) = 8
（四）课堂练习（10 分钟）
在 Rt△ABC 中，∠C = 90°，a = 5，c = 13，求 sinB、cosB、tanB 的值。
已知在 Rt△ABC 中，∠C = 90°，cosA = 4/5 ，c = 15，求 a 和 b 的值。
学生独立完成练习，教师巡视指导，及时纠正学生的错误。
（五）课堂小结（5 分钟）
与学生一起回顾锐角三角函数的定义，包括正弦、余弦、正切函数的表达式。
总结根据直角三角形边长求锐角三角函数值以及已知锐角三角函数值和一边长求其他边长的方法。
强调锐角三角函数值与角度的对应关系。
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
正切的概念
知1－讲
1
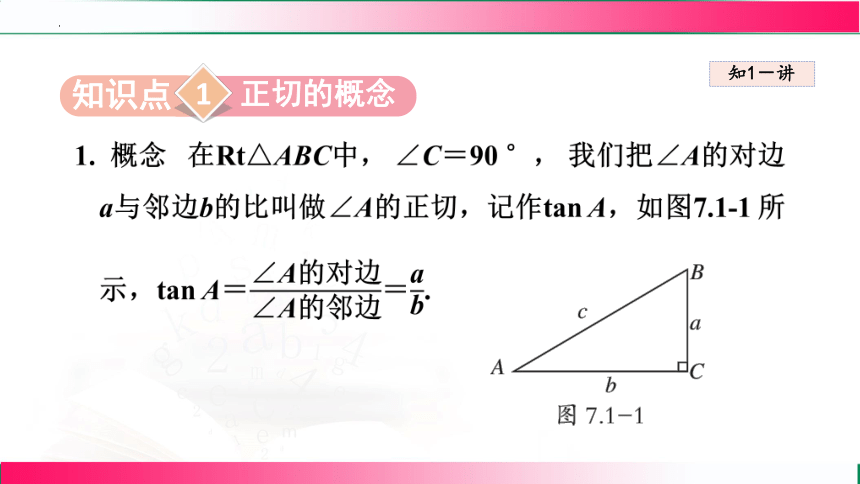
1. 概念 在Rt△ABC中， ∠C＝90 °， 我们把∠A的对边a与邻边b的比叫做∠A的正切，记作tan A，如图7.1-1 所示，tan A＝＝.
知1－讲
2. 表示法
(1)正切值的大小只与锐角的大小有关，而与所在的直角三角形的边长的大小无关.
(2)tan A表示∠A的正切， 习惯上省去角的符号“∠”，但当角是用三个大写字母或数字表示时，它的正切不能省略角的符号“∠”，如tan ∠ABC，tan ∠1.
知1－讲
特别警示
tan A是一个完整的符号，不能写成tan·A或者看成tan与A的积，离开A 的tan没有任何意义，只有合起来才表示∠A的正切.
知1－练
例 1
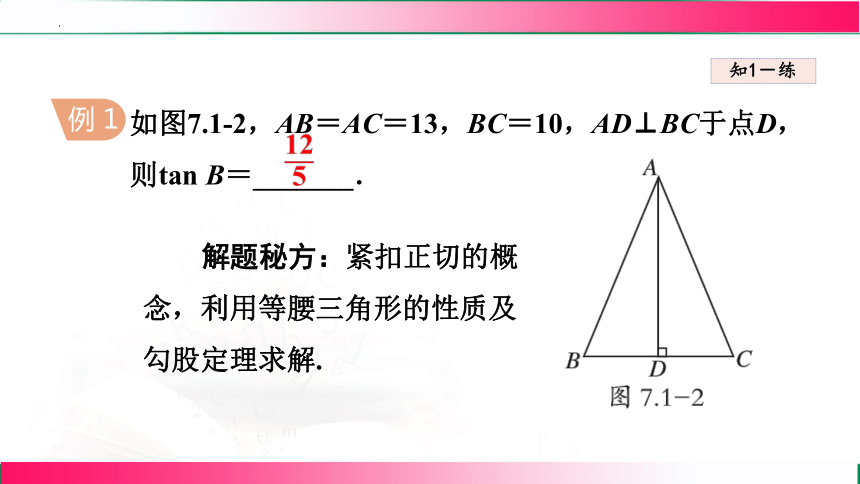
如图7.1-2，AB＝AC＝13，BC＝10，AD⊥BC于点D，则tan B＝_______．
解题秘方：紧扣正切的概念，利用等腰三角形的性质及勾股定理求解.
知1－练
解：∵ AB＝AC，AD⊥BC，∴ BD＝BC＝5．
在Rt△ABD中，根据勾股定理，得
AD＝＝＝12．
∴ tan B＝＝．
知1－练
[中考·凉山州] 如图7.1-3，△ABC的顶点在正方形网格的格点上，则tan A的值为(　　)
A. B.
C. 2 D. 2
解题秘方：紧扣“构造法”构造直角三角形，根据网格的结构特征及勾股定理可求出tan A的值．
例 2
知1－练
解：如图7.1-3 所示，取格点D，连接BD．
假设正方形网格的边长为1，由网格的结构特
征，得BD2＝2，AD2＝8，AB2＝10，故BD2＋
AD2＝AB2. 故BD⊥AC.
由AD＝＝2，BD＝，得tan A＝＝＝.
答案：A
知1－练
例 3
如图7.1-4， 在Rt△ABC中， ∠C＝90 °，AB＝10，
tan A＝，则BC的长为(　　)
A. 2 B. 6 C. 8 D. 10
解题秘方：紧扣正切的概念，用含k的代数式表示出BC和AC，然后根据勾股定理即可求解．
知1－练
解：在Rt△ABC中，设BC＝3k(k＞0).
因为tan A＝＝，所以AC＝4 k.
由勾股定理，得BC2＋AC2＝AB2，即(3k)2＋(4k)2＝102.
解得k＝2(负值舍去). 所以BC＝3k＝6.
答案：B
知3－讲
知识点
正切值的变化规律
2
1. 性质 锐角的正切值随着锐角的增大而增大.
2. 锐角α与β的正切值的变化规律
(1)若0°<α<90°，0°<β<90°， 则tan α>0， tan β>0.
(2)若α>β，则tan α>tan β；若α<β，则tan α知3－讲
特别警示
不是角度增大到原来的几倍，正切值就增大到原来的几倍.
知3－练
用“<”连接下列各式：tan 15°、tan 30°、tan 60°、tan 75°.
例 5
解题秘方：紧扣锐角正切值的变化规律即可求解.
解：因为15°< 30°< 60°< 75°,
所以tan 15°< tan 30°< tan 60°< tan 75°.
返回
2.
B
返回
3.
D
返回
4.
A
如图，△ABC的顶点都在正方形网格的格点上，则tan A的值为(　　)
返回
5.
3.73
[2024南京鼓楼区校级月考]用计算器求得tan 75°≈________(精确到0.01)．
返回
6.
＜
比较大小：tan 40°________tan 50°(填“＞”“＝”或“＜”)．
返回
7.
返回
8.
9
9.
如图，在矩形ABCD中，AB＝10，BC＝8，E为AD边上一点，沿CE将△CDE对折，使点D正好落在AB边上的点F处，求tan∠AFE.
返回
返回
10.
C
返回
11.
在等边三角形ABC中，点D在射线CA上，且AB＝2AD，则tan∠DBC的值为________．
返回
12.
[2024江西]将图①所示的七巧板，拼成图②所示的
四边形ABCD，连接AC，则tan∠CAB＝________.
正切
正
切
计
算
锐角的正切值
线段的长度
正切值的
变化规律
概
念
在Rt△ABC中，
∠C＝90°
tan A＝
谢谢观看！