7.6.1 与坡度和坡角有关的问题 课件(共25张PPT)
文档属性
| 名称 | 7.6.1 与坡度和坡角有关的问题 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
7.6.1 与坡度和坡角有关的问题
第7章 锐角三角函数
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
在黑板上画出一个直角三角形 ABC,其中∠C = 90°。设∠A、∠B、∠C 所对的边分别为 a、b、c。
正弦函数定义
引导学生观察∠A 的对边 a 与斜边 c 的比值,给出正弦函数的定义:在 Rt△ABC 中,锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA,即 sinA = a/c 。通过多个不同边长的直角三角形示例,让学生计算∠A 的正弦值,加深对定义的理解。
余弦函数定义
类比正弦函数,讲解余弦函数:锐角 A 的邻边 b 与斜边 c 的比叫做∠A 的余弦,记作 cosA,即 cosA = b/c 。同样通过实例计算强化概念。
正切函数定义
介绍正切函数:锐角 A 的对边 a 与邻边 b 的比叫做∠A 的正切,记作 tanA,即 tanA = a/b 。引导学生分析正切函数与正弦、余弦函数的区别与联系。
(三)例题讲解(15 分钟)
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
有关坡角、坡度的应用
知1-讲
1
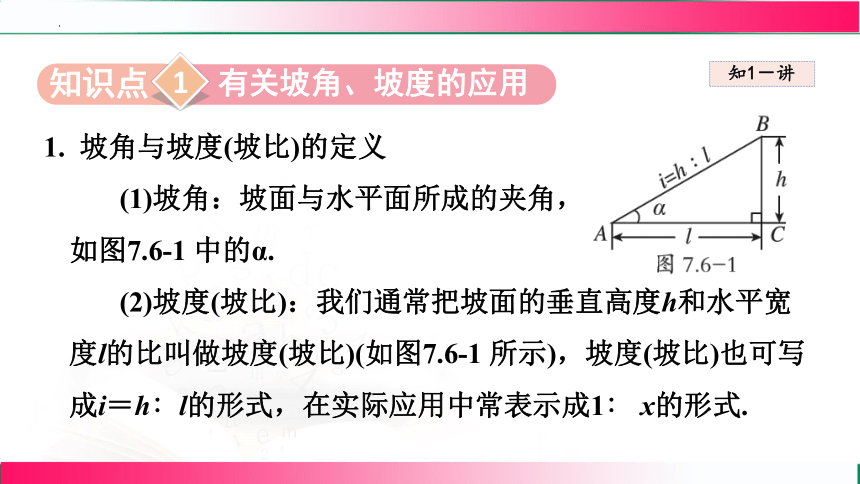
1. 坡角与坡度(坡比)的定义
(1)坡角:坡面与水平面所成的夹角,
如图7.6-1 中的α.
(2)坡度(坡比):我们通常把坡面的垂直高度h和水平宽度l的比叫做坡度(坡比)(如图7.6-1 所示),坡度(坡比)也可写成i=h∶l的形式,在实际应用中常表示成1∶ x的形式.
知1-讲
2. 坡度与坡角的关系 i==tan α,即坡度是坡角的正切
值,坡角越大,坡度也就越大.
3. 基本图形及关系式
图形 关系式 图形 关系式
BC=BD+DC=AD· BC=BE+EF+CF=BE+AD+CF=AD+h·
知1-讲
4. 解决实际问题的一般步骤
(1)画出平面图形,将实际问题抽象为数学问题,转化为解直角三角形的问题;
(2)根据已知条件的特点,灵活选用锐角三角函数等知识解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知1-讲
特别提醒
①坡度是两条线段的比值,不是度数.
②表示坡度时,通常把比的前项取作1,后项可以是小数.
③物体的倾斜程度通常可用物体的坡度表示,坡度越大,坡角越大,坡面越陡;反之,坡度越小,坡角越小,坡面越缓.
知1-讲
特别提醒
当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
知1-练
例 1
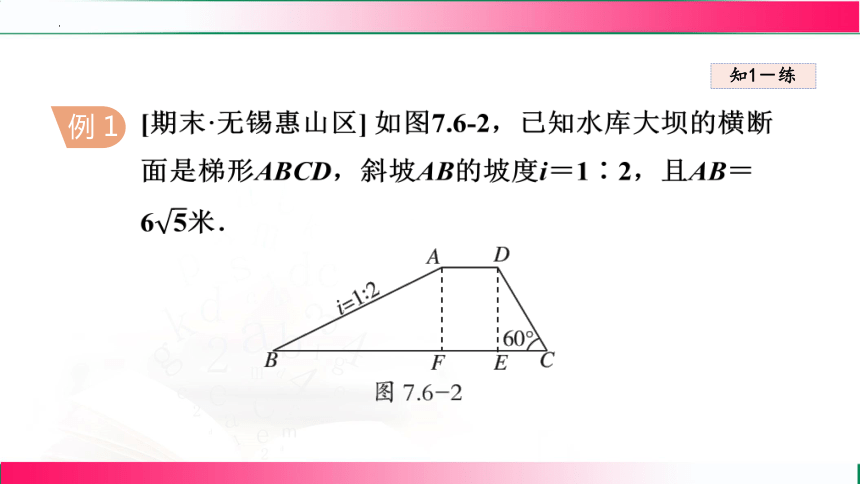
[期末·无锡惠山区] 如图7.6-2,已知水库大坝的横断面是梯形ABCD,斜坡AB的坡度i=1∶2,且AB=6米.
知1-练
(1)求水库大坝的高度;
解题秘方:过点A作AF⊥BC于点F,可得AF 为坝高,根据坡度的定义与勾股定理进行计算即可得到答案;
知1-练
解:如图7.6-2,过点A作AF⊥BC于点F.
∵ i=1∶2,∴ AF∶BF=1∶2.
设AF=x米,则BF=2x米.
在Rt△ABF中,由勾股定理,
得x2+(2x)2=(6)2,解得x=6(负值舍去),
∴ AF=6 米,BF=12 米.
答:水库大坝的高度为6 米.
知1-练
(2)若坝顶AD=4 米,斜坡CD的坡角为60°. 求坝底BC的长(结果保留根号).
解题秘方:过点D作DE⊥BC于点E,可得四边形AFED为矩形,得到相应线段的长,再结合tan 60°的值求得CE的长.
知1-练
解:如图7.6-2,过点D作DE⊥BC于点E,则四边形AFED 为矩形,∴ EF=AD=4 米,DE=AF=6 米.
在Rt△DEC中,∵∠C=60°,
∴ EC== 2米,
∴ BC=BF+EF+CE=12+4+2=16+2(米).
答:坝底BC的长为(16+2)米.
知1-练
方法点拨
此题是教材问题1的改编, 在解与坡角、坡度有关的问题时,通常紧扣坡度、坡角的定义,利用锐角三角函数和勾股定理等知识计算求解;有时还需根据实际问题进行画图,根据需要作出辅助线,常常添加垂线或平行线,构造直角三角形和矩形.
返回
D
1.
如图,滑雪场有一坡角为20°的滑雪道,滑雪道AC长为200米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
返回
2.
A
[2024南通崇川区校级月考]如图,某公园入口处原有三级台阶,每级台阶高为18 cm,宽为30 cm,为方便残障人士,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
A.210 cm B.120 cm
C.504 cm D.60 cm
返回
3.
115°
一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为________.
返回
4.
16
5.
为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD的长为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
返回
返回
6.
[2024眉山]如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为____________米.
7.
如图,在河流两边有甲、乙两座山,现在从甲山A处的位置向乙山B处拉电线.已知甲山上A点到河边C的距离AC=130米,点A到CD的垂直高度为120米;乙山BD的坡比为4:3,乙山上B点到河边D的距离BD=450米,从B处看A处的俯角为25°.(参考值:sin 25°≈0.423,cos 25°≈0.906,tan 25°≈0.466)
(1)求乙山B处到河边CD的垂直高度;
解:过点A作AE⊥CD于点E,过点A作AH⊥BF于点H,
则四边形AEFH为矩形,
∴HF=AE=120米,AH=EF.
∴BH=BF-HF=360-120=240(米).
∵从B处看A处的俯角为25°,∴∠BAH=25°.
(2)求河CD的宽度.(结果保留整数)
返回
谢谢观看!
7.6.1 与坡度和坡角有关的问题
第7章 锐角三角函数
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
在黑板上画出一个直角三角形 ABC,其中∠C = 90°。设∠A、∠B、∠C 所对的边分别为 a、b、c。
正弦函数定义
引导学生观察∠A 的对边 a 与斜边 c 的比值,给出正弦函数的定义:在 Rt△ABC 中,锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA,即 sinA = a/c 。通过多个不同边长的直角三角形示例,让学生计算∠A 的正弦值,加深对定义的理解。
余弦函数定义
类比正弦函数,讲解余弦函数:锐角 A 的邻边 b 与斜边 c 的比叫做∠A 的余弦,记作 cosA,即 cosA = b/c 。同样通过实例计算强化概念。
正切函数定义
介绍正切函数:锐角 A 的对边 a 与邻边 b 的比叫做∠A 的正切,记作 tanA,即 tanA = a/b 。引导学生分析正切函数与正弦、余弦函数的区别与联系。
(三)例题讲解(15 分钟)
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
有关坡角、坡度的应用
知1-讲
1
1. 坡角与坡度(坡比)的定义
(1)坡角:坡面与水平面所成的夹角,
如图7.6-1 中的α.
(2)坡度(坡比):我们通常把坡面的垂直高度h和水平宽度l的比叫做坡度(坡比)(如图7.6-1 所示),坡度(坡比)也可写成i=h∶l的形式,在实际应用中常表示成1∶ x的形式.
知1-讲
2. 坡度与坡角的关系 i==tan α,即坡度是坡角的正切
值,坡角越大,坡度也就越大.
3. 基本图形及关系式
图形 关系式 图形 关系式
BC=BD+DC=AD· BC=BE+EF+CF=BE+AD+CF=AD+h·
知1-讲
4. 解决实际问题的一般步骤
(1)画出平面图形,将实际问题抽象为数学问题,转化为解直角三角形的问题;
(2)根据已知条件的特点,灵活选用锐角三角函数等知识解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知1-讲
特别提醒
①坡度是两条线段的比值,不是度数.
②表示坡度时,通常把比的前项取作1,后项可以是小数.
③物体的倾斜程度通常可用物体的坡度表示,坡度越大,坡角越大,坡面越陡;反之,坡度越小,坡角越小,坡面越缓.
知1-讲
特别提醒
当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
知1-练
例 1
[期末·无锡惠山区] 如图7.6-2,已知水库大坝的横断面是梯形ABCD,斜坡AB的坡度i=1∶2,且AB=6米.
知1-练
(1)求水库大坝的高度;
解题秘方:过点A作AF⊥BC于点F,可得AF 为坝高,根据坡度的定义与勾股定理进行计算即可得到答案;
知1-练
解:如图7.6-2,过点A作AF⊥BC于点F.
∵ i=1∶2,∴ AF∶BF=1∶2.
设AF=x米,则BF=2x米.
在Rt△ABF中,由勾股定理,
得x2+(2x)2=(6)2,解得x=6(负值舍去),
∴ AF=6 米,BF=12 米.
答:水库大坝的高度为6 米.
知1-练
(2)若坝顶AD=4 米,斜坡CD的坡角为60°. 求坝底BC的长(结果保留根号).
解题秘方:过点D作DE⊥BC于点E,可得四边形AFED为矩形,得到相应线段的长,再结合tan 60°的值求得CE的长.
知1-练
解:如图7.6-2,过点D作DE⊥BC于点E,则四边形AFED 为矩形,∴ EF=AD=4 米,DE=AF=6 米.
在Rt△DEC中,∵∠C=60°,
∴ EC== 2米,
∴ BC=BF+EF+CE=12+4+2=16+2(米).
答:坝底BC的长为(16+2)米.
知1-练
方法点拨
此题是教材问题1的改编, 在解与坡角、坡度有关的问题时,通常紧扣坡度、坡角的定义,利用锐角三角函数和勾股定理等知识计算求解;有时还需根据实际问题进行画图,根据需要作出辅助线,常常添加垂线或平行线,构造直角三角形和矩形.
返回
D
1.
如图,滑雪场有一坡角为20°的滑雪道,滑雪道AC长为200米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
返回
2.
A
[2024南通崇川区校级月考]如图,某公园入口处原有三级台阶,每级台阶高为18 cm,宽为30 cm,为方便残障人士,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
A.210 cm B.120 cm
C.504 cm D.60 cm
返回
3.
115°
一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为________.
返回
4.
16
5.
为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD的长为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
返回
返回
6.
[2024眉山]如图,斜坡CD的坡度i=1:2,在斜坡上有一棵垂直于水平面的大树AB,当太阳光与水平面的夹角为60°时,大树在斜坡上的影子BE长为10米,则大树AB的高为____________米.
7.
如图,在河流两边有甲、乙两座山,现在从甲山A处的位置向乙山B处拉电线.已知甲山上A点到河边C的距离AC=130米,点A到CD的垂直高度为120米;乙山BD的坡比为4:3,乙山上B点到河边D的距离BD=450米,从B处看A处的俯角为25°.(参考值:sin 25°≈0.423,cos 25°≈0.906,tan 25°≈0.466)
(1)求乙山B处到河边CD的垂直高度;
解:过点A作AE⊥CD于点E,过点A作AH⊥BF于点H,
则四边形AEFH为矩形,
∴HF=AE=120米,AH=EF.
∴BH=BF-HF=360-120=240(米).
∵从B处看A处的俯角为25°,∴∠BAH=25°.
(2)求河CD的宽度.(结果保留整数)
返回
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
