8.6 收取多少保险费才合理 课件(共21张PPT)
文档属性
| 名称 | 8.6 收取多少保险费才合理 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 18:12:15 | ||
图片预览







文档简介
(共21张PPT)
8.6 收取多少保险费才合理
第8章 统计和概率的简单应用
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
数据收集:讲解数据收集的常见方法,如问卷调查、实地观察、查阅资料等。以 “调查班级同学的兴趣爱好” 为例,详细说明如何设计问卷,包括问题的设置、选项的合理性等。强调数据收集过程中要保证数据的真实性、准确性和完整性。
数据整理与描述:介绍数据整理的步骤,将收集到的数据进行分类、排序。通过具体数据,如班级同学的身高数据,展示如何制作频数分布表。随后讲解不同统计图表的特点与绘制方法:
条形图:直观展示不同类别数据的数量大小对比,以 “各学科成绩优秀人数统计” 为例绘制条形图。
折线图:突出数据的变化趋势,以 “某地区一年中每月平均气温变化” 为例绘制折线图。
扇形图:体现各部分在总体中所占的比例关系,以 “家庭每月支出项目占比” 为例绘制扇形图。
数据分析:讲解常用的统计量,如平均数、中位数和众数。通过一组学生考试成绩数据,分别计算这三个统计量,解释它们各自反映数据的哪些特征,以及在不同情境下如何合理选择统计量来描述数据集中趋势。
概率部分
随机事件:通过抛硬币、掷骰子等简单实验,引入随机事件的概念,让学生明确必然事件、不可能事件和随机事件的区别。列举生活中的事件,如 “明天会下雨”“购买彩票中奖” 等,让学生判断其事件类型。
概率计算:给出概率的定义和计算公式,以掷骰子为例,计算掷出偶数点的概率。通过更多简单实例,如从装有不同颜色球的袋子中摸球,强化学生对概率公式的理解与运用,同时强调概率值的范围在 0 到 1 之间。
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
概率的含义
知1-讲
1
一般地,如果随机事件A发生的概率是P(A),那么在相同的条件下重复n次试验,事件A发生的次数的平均值为n×P(A).
类似地,如果奖券中奖的概率为0.01,并不能肯定在100张奖券中必有1张中奖,而是指当购买的奖券数量很大时,在100张一组的奖券中,平均会有(100×0.01)张,即1张中奖.
知1-练
例 1
[期末·无锡] 下列说法正确的是( )
A. 任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B. 天气预报说“明天降雨的概率为40%”,表明明天有40% 的时间会降雨
C. “彩票中奖的概率是”表示买8张彩票一定会有1张中奖
D. “篮球队员在罚球线上投篮一次,投中”为随机事件
知2-讲
知识点
概率的实际应用
2
利用概率可以帮助保险业做出不亏本的决策,先通过试验和分析求出事件的概率,然后运用概率知识,结合不亏本的原则,即可判断出某种保险的收费情况. 运用概率的大小还可以对其他随机事件做出预估或预测,解决一些实际问题.
知2-练
已知袋中有5个红球、18个白球、17个黄球,这些球除颜色外都相同,从中任取1个球,放回,再从中任取1个球,经过多次重复试验,平均多少次才会从中取到1个红球?
例 2
解题秘方:紧扣“概率的含义以及事件A发生的次数的平均值为n×P(A)”即可求解.
知2-练
解:从袋中任取1 个球是红球的概率为=.
设平均n次才会从中取到1个红球,n次共取到n个球,
∴在这n个球中,取到红球的平均次数为n×,
即n×=1.
∴ n=8,即平均8次才会从中取到1个红球.
知2-练
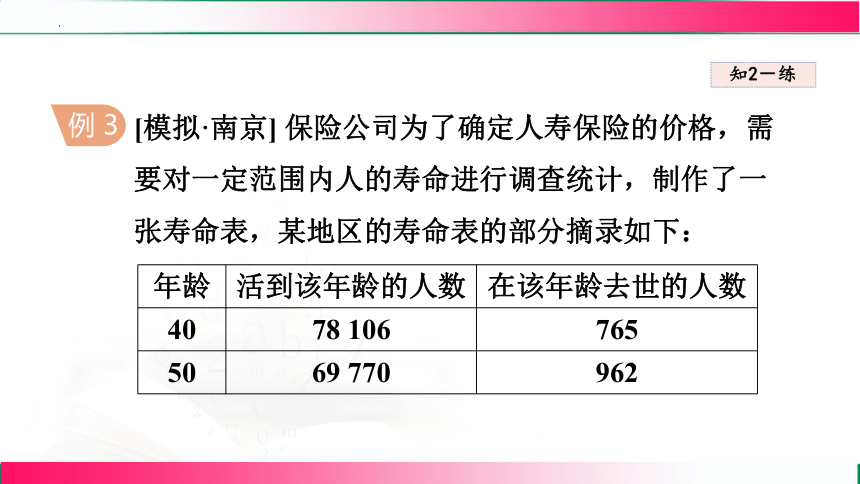
[模拟·南京] 保险公司为了确定人寿保险的价格,需要对一定范围内人的寿命进行调查统计,制作了一张寿命表,某地区的寿命表的部分摘录如下:
例 3
年龄 活到该年龄的人数 在该年龄去世的人数
40 78 106 765
50 69 770 962
知2-练
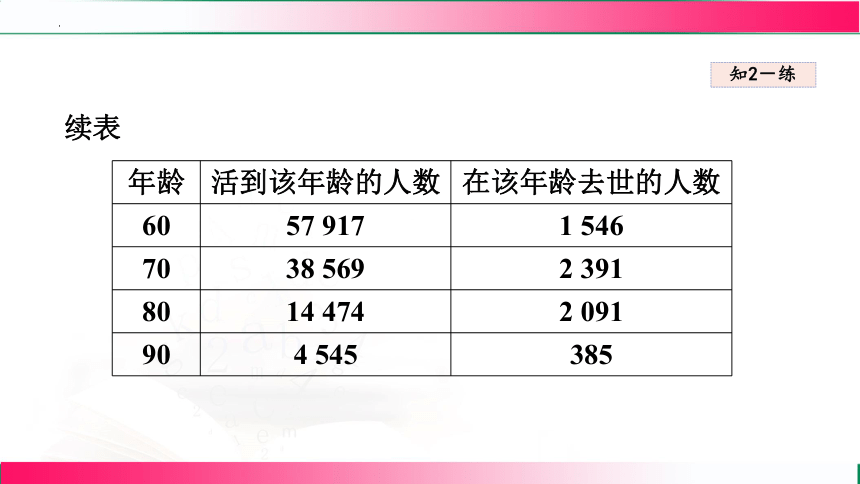
续表
年龄 活到该年龄的人数 在该年龄去世的人数
60 57 917 1 546
70 38 569 2 391
80 14 474 2 091
90 4 545 385
知2-练
根据上表解答下列问题:
(1)某人今年40 岁, 他当年去世的概率是多少?他活到80 岁的概率是多少?(精确到0.000 1)
解:他当年去世的概率是≈ 0.009 8.
他活到80岁的概率是≈ 0.185 3.
知2-练
(2)如果有20 000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,保险公司怎样收费才能不亏本?(精确到1 元)
知2-练
解:设每年每人收取x元保险费.
根据题意,得20 000x ≥×20 000×100 000,
解得x ≥ 1 379.
答:每年每人至少收取1 379元保险费,保险公司才能
不亏本.
返回
A
1.
[2024海安期末]先后两次抛掷同一枚质地均匀的硬币,则第一次正面向上、第二次反面向上的概率是( )
返回
2.
C
[2024滨海期末]某个事件发生的概率是0.5,这意味着( )
A.在一次试验中没有发生,下次肯定发生
B.在一次试验中已经发生,下次肯定不发生
C.每次试验中事件发生的可能性是50%
D.在两次重复试验中该事件必有一次发生
返回
3.
30
某产品出现次品的概率为0.05,任意抽取这种产品
600件,那么大约有________件是次品.
返回
4.
20
返回
5.
30
[2024南京玄武区校级月考]某航班每次约有200名乘客,一次飞行中飞机失事的概率P=0.000 05,某保险公司为乘客提供保险,承诺飞机一旦失事,向每名乘客赔偿60万元人民币.平均来说,保险公司应该至少向每名乘客收取________元保险费才不亏本.
6.
返回
解:小明的想法不对.理由:因为小明将本次抽奖活动中奖率为50%,一等奖中奖率为10%,理解错了,其中的50%,10%是针对所有的奖券而言,而不是任抽几张,这几张的10%为一等奖,50%都获奖,所抽取的几张,可能都中奖,也可能都没有中奖.
收取多少保险费才合理
收取多少保险
费才合理
概率的含义
事件A发生的次数的
平均值n×P(A)的应用
利用概率解
决保险问题
利用概率解决
转盘获奖问题
谢谢观看!
8.6 收取多少保险费才合理
第8章 统计和概率的简单应用
苏科版数学九年级下册【示范课精品课件】
授课教师:********
班 级:********
时 间:********
数据收集:讲解数据收集的常见方法,如问卷调查、实地观察、查阅资料等。以 “调查班级同学的兴趣爱好” 为例,详细说明如何设计问卷,包括问题的设置、选项的合理性等。强调数据收集过程中要保证数据的真实性、准确性和完整性。
数据整理与描述:介绍数据整理的步骤,将收集到的数据进行分类、排序。通过具体数据,如班级同学的身高数据,展示如何制作频数分布表。随后讲解不同统计图表的特点与绘制方法:
条形图:直观展示不同类别数据的数量大小对比,以 “各学科成绩优秀人数统计” 为例绘制条形图。
折线图:突出数据的变化趋势,以 “某地区一年中每月平均气温变化” 为例绘制折线图。
扇形图:体现各部分在总体中所占的比例关系,以 “家庭每月支出项目占比” 为例绘制扇形图。
数据分析:讲解常用的统计量,如平均数、中位数和众数。通过一组学生考试成绩数据,分别计算这三个统计量,解释它们各自反映数据的哪些特征,以及在不同情境下如何合理选择统计量来描述数据集中趋势。
概率部分
随机事件:通过抛硬币、掷骰子等简单实验,引入随机事件的概念,让学生明确必然事件、不可能事件和随机事件的区别。列举生活中的事件,如 “明天会下雨”“购买彩票中奖” 等,让学生判断其事件类型。
概率计算:给出概率的定义和计算公式,以掷骰子为例,计算掷出偶数点的概率。通过更多简单实例,如从装有不同颜色球的袋子中摸球,强化学生对概率公式的理解与运用,同时强调概率值的范围在 0 到 1 之间。
5
课堂检测
4
新知讲解
6
变式训练
7
考试考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
概率的含义
知1-讲
1
一般地,如果随机事件A发生的概率是P(A),那么在相同的条件下重复n次试验,事件A发生的次数的平均值为n×P(A).
类似地,如果奖券中奖的概率为0.01,并不能肯定在100张奖券中必有1张中奖,而是指当购买的奖券数量很大时,在100张一组的奖券中,平均会有(100×0.01)张,即1张中奖.
知1-练
例 1
[期末·无锡] 下列说法正确的是( )
A. 任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B. 天气预报说“明天降雨的概率为40%”,表明明天有40% 的时间会降雨
C. “彩票中奖的概率是”表示买8张彩票一定会有1张中奖
D. “篮球队员在罚球线上投篮一次,投中”为随机事件
知2-讲
知识点
概率的实际应用
2
利用概率可以帮助保险业做出不亏本的决策,先通过试验和分析求出事件的概率,然后运用概率知识,结合不亏本的原则,即可判断出某种保险的收费情况. 运用概率的大小还可以对其他随机事件做出预估或预测,解决一些实际问题.
知2-练
已知袋中有5个红球、18个白球、17个黄球,这些球除颜色外都相同,从中任取1个球,放回,再从中任取1个球,经过多次重复试验,平均多少次才会从中取到1个红球?
例 2
解题秘方:紧扣“概率的含义以及事件A发生的次数的平均值为n×P(A)”即可求解.
知2-练
解:从袋中任取1 个球是红球的概率为=.
设平均n次才会从中取到1个红球,n次共取到n个球,
∴在这n个球中,取到红球的平均次数为n×,
即n×=1.
∴ n=8,即平均8次才会从中取到1个红球.
知2-练
[模拟·南京] 保险公司为了确定人寿保险的价格,需要对一定范围内人的寿命进行调查统计,制作了一张寿命表,某地区的寿命表的部分摘录如下:
例 3
年龄 活到该年龄的人数 在该年龄去世的人数
40 78 106 765
50 69 770 962
知2-练
续表
年龄 活到该年龄的人数 在该年龄去世的人数
60 57 917 1 546
70 38 569 2 391
80 14 474 2 091
90 4 545 385
知2-练
根据上表解答下列问题:
(1)某人今年40 岁, 他当年去世的概率是多少?他活到80 岁的概率是多少?(精确到0.000 1)
解:他当年去世的概率是≈ 0.009 8.
他活到80岁的概率是≈ 0.185 3.
知2-练
(2)如果有20 000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,保险公司怎样收费才能不亏本?(精确到1 元)
知2-练
解:设每年每人收取x元保险费.
根据题意,得20 000x ≥×20 000×100 000,
解得x ≥ 1 379.
答:每年每人至少收取1 379元保险费,保险公司才能
不亏本.
返回
A
1.
[2024海安期末]先后两次抛掷同一枚质地均匀的硬币,则第一次正面向上、第二次反面向上的概率是( )
返回
2.
C
[2024滨海期末]某个事件发生的概率是0.5,这意味着( )
A.在一次试验中没有发生,下次肯定发生
B.在一次试验中已经发生,下次肯定不发生
C.每次试验中事件发生的可能性是50%
D.在两次重复试验中该事件必有一次发生
返回
3.
30
某产品出现次品的概率为0.05,任意抽取这种产品
600件,那么大约有________件是次品.
返回
4.
20
返回
5.
30
[2024南京玄武区校级月考]某航班每次约有200名乘客,一次飞行中飞机失事的概率P=0.000 05,某保险公司为乘客提供保险,承诺飞机一旦失事,向每名乘客赔偿60万元人民币.平均来说,保险公司应该至少向每名乘客收取________元保险费才不亏本.
6.
返回
解:小明的想法不对.理由:因为小明将本次抽奖活动中奖率为50%,一等奖中奖率为10%,理解错了,其中的50%,10%是针对所有的奖券而言,而不是任抽几张,这几张的10%为一等奖,50%都获奖,所抽取的几张,可能都中奖,也可能都没有中奖.
收取多少保险费才合理
收取多少保险
费才合理
概率的含义
事件A发生的次数的
平均值n×P(A)的应用
利用概率解
决保险问题
利用概率解决
转盘获奖问题
谢谢观看!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
