北师大八下6.3中位线

(共29张PPT)
第六章 平行四边形
6.3中位线
北师大版 数学 八年级 下册
学习目标
3.利用三角形中位线定理解决问题.
1.理解并掌握三角形中位线的概念
2.理解并掌握三角形中位线的性质定理及其推导过程
情景导入
1.平行四边形的性质和判定有哪些？
边：
角：
对角线：
B
O
D
A
C
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AB=CD
∠BAD=∠BCD，∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
情景导入
古时候，有位老汉有四个儿子，他有一块三角形的耕地，想分给四个儿子。他们的儿子说必须分成一模一样的四部分才公平。这可难坏了老汉，你能帮帮他吗？
B
C
A
情景导入
小明同学把三角形分成了四个全等的三角形，猜一猜他是怎样做的？
做法:连接每两边的中点.
B
C
A
D·
·E
·
F
核心知识点一：
三角形的中位线及其性质
B
C
A
D·
·E
·
F
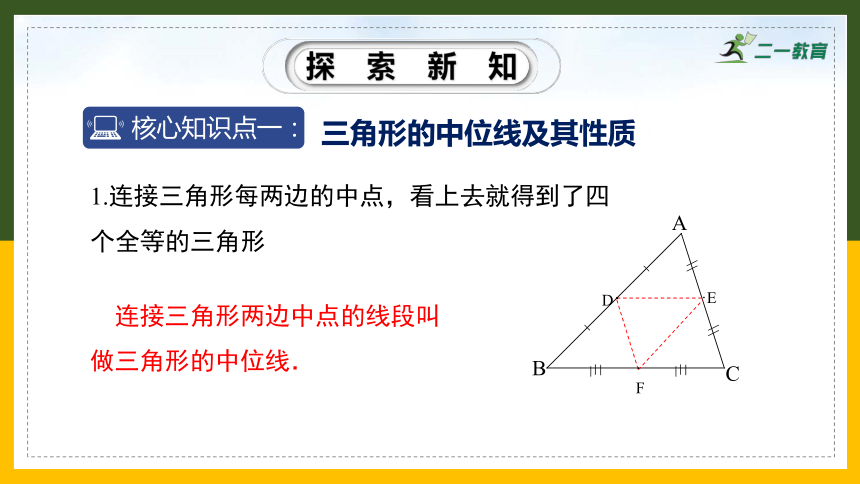
1.连接三角形每两边的中点，看上去就得到了四个全等的三角形
连接三角形两边中点的线段叫做三角形的中位线．
探索新知
2.三角形的中位线定义的两层含义：
（2）∵ DE为△ABC的中位线，
（1）∵D、E分别为AB、AC的中点，
∴DE为△ABC的中位线．
∴ D、E分别为AB、AC的中点．
B
C
A
D·
·E
·
F
探索新知
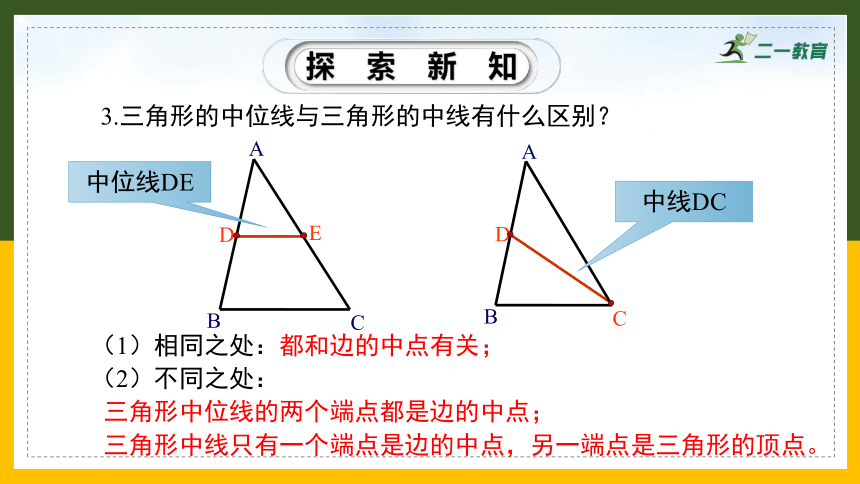
3.三角形的中位线与三角形的中线有什么区别？
（1）相同之处：都和边的中点有关；
（2）不同之处：
三角形中位线的两个端点都是边的中点；
三角形中线只有一个端点是边的中点，另一端点是三角形的顶点。
C
B
A
E
D
C
B
A
D
中线DC
中位线DE
探索新知
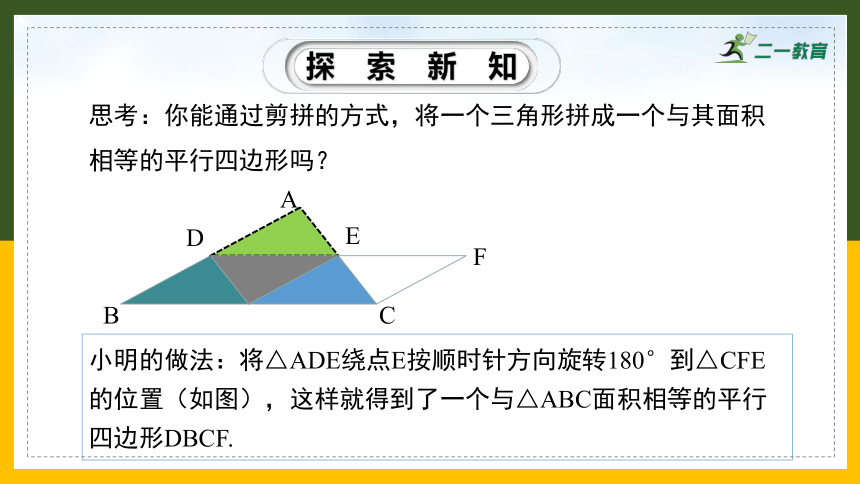
思考：你能通过剪拼的方式，将一个三角形拼成一个与其面积相等的平行四边形吗？
小明的做法：将△ADE绕点E按顺时针方向旋转180°到△CFE的位置（如图），这样就得到了一个与△ABC面积相等的平行四边形DBCF.
A
D
E
F
C
B
探索新知
通过上面的旋转变换，你能猜想出三角形的中位线与第三边有什么关系吗？
A
B
C
D
F
E
DE和边BC关系
数量关系：
位置关系：
DE//BC
DE＝ BC
探索新知
已知：在△ABC中，D、E分别是△ABC的边AB、AC的中点.
求证：DE∥BC,
探索新知
F
∵CF∥AB，
∴∠A=∠ECF
又∵AE=EC，∠AED=∠CEF
∴△ADE≌△CFE（ASA）
∴ AD=FC
又∵DB=AD，
∴DB=FC
∴四边形BCFD是平行四边形．
∴DE// BC 且DE=EF= BC ．
证明1：过点C作CF∥AB交DE的延长线于F
探索新知
F
证明2:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE,∠AED=∠CEF,
∴△ADE≌△CFE(SAS).
∴AD=CF,∠ADE=∠F.
∴BD∥CF.
∵AD=BD,
∴BD=CF.
∴四边形DBCF是平行四边形.
∴DF∥BC,DF=BC.
∴DE∥BC,且DE=EF= BC ．
探索新知
F
B
C
E
D
A
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形．
∴AD=FC，AD∥FC
又∵ AD=BD，
∴DB=FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC ．
证明3：如图，延长DE至F， 使EF=DE，连接CD、AF、CF，
探索新知
归纳总结
三角形中位线定理：
三角形的中位线平行于第三边，并且等于第三边的一半.
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴DE∥BC,
三角形中位线定理有两个结论：
（1）表示位置关系------平行于第三边；
（2）表示数量关系------等于第三边的一半。
探索新知
核心知识点二：
中点四边形
如图，任意画一个四边形，以四边形的中点为顶点组成一个新四边形，这个新四边形的形状有什么特征？请证明你的结论，并与同伴交流.
探索新知
证明：如图，连接AC.
∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴EF∥AC，EF= AC，HG∥AC，HG= AC.
∴EF∥HG，EF=HG.
∴四边形EFGH为平行四边形.
中点四边形的定义：
依次连接任意四边形各边中点所得到的四边形称为中点四边形．
拓展：不管四边形的形状怎样改变，中点四边形始终是平行四边形．
探索新知
任意四边形的中点四边形都是 ；
平行四边形的中点四边形是 ；
矩形的中点四边形是 ；
菱形的中点四边形是 ；
正方形的中点四边形是 。
平行四边形
平行四边形
矩形
菱形
正方形
小组合作探究:
探索新知
归纳总结
实际上，顺次连接四边形各边中点所得到的四边形一定是平行四边形，但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等，与是否互相平分无关.
探索新知
归纳总结
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
探索新知
当堂检测
1.在 中，点 ， 分别是边 ， 的中点， ，
则 ( ) .
C
A．2 B．2.5 C．3 D．3.5
2.顺次连接四边形四边中点所得的四边形一定是( ) .
A
A．平行四边形 B．矩形 C．菱形 D．正方形
当堂检测
3.如图，在 中， ， ，点
为 上一点， ， 于点 ，点
为 的中点，连接 ，则 的长为( ) .
B
A．1 B．2 C．3 D．4
4.如图，要测定被池塘隔开的 ， 两点的距离,可以在 外选一点 ，连接 ， ，并分别找出它们的中
点 ， ，连接 .现测得 ， ，
，则 ( ) .
B
A． B． C． D．
当堂检测
5.如图，在平行四边形 中，对角线 ， 相交于
点 ，点 ， 分别是 ， 的中点，连接 ，若
，则 的长为( ) .
A
A．12 B．6 C．3 D．1.5
6.如图， 的对角线 ， 相交于点 ，点 是
的中点，若 ， 的周长为10，则
的周长为( ) .
B
A．20 B．24 C．28 D．32
当堂检测
7.如图，在 中， ， 是 边上的中
线， 是 的中位线，若 ，则 的长为( ) .
A
A．10 B．5 C．8 D．6
8.如图，在平行四边形 中，对角线 与 相交于点 ， 是边 的中点，连接 .若 ，
，则 _____.
当堂检测
9.如图，在△ABC中，点D在BC上，且CD＝CA，CF平分∠ACB，AE＝EB.求证：EF＝BD.
证明：∵CD＝CA，CF平分∠ACB，
∴F是AD的中点.
∵AE＝EB.
∴E是AB的中点，
∴EF是△ABD的中位线，
∴EF＝BD.
当堂检测
10.如图，在△ABC中，D，E分别是AC，AB的中点，F是CB的延长线上一点，且CF＝3BF，连接DB，EF.
（1）求证：四边形DEFB是平行四边形；
（1）证明：∵D，E分别是AC，AB的中点，
∴DE∥BC， BC＝2DE.
∵CF＝3BF，
∴BC＝2BF，∴DE＝BF，
∴四边形DEFB是平行四边形.
当堂检测
（2）若∠ACB＝90°，AC＝12，DE＝4，求四边形DEFB的周长.
（2）解：∵DE＝4，
∴BC＝2DE＝8，BF＝DE＝4.
∵四边形DEFB是平行四边形，
∴BD＝EF.
∵D是AC的中点，
∴CD＝AC＝6.
∵∠ACB＝90°，
∴BD＝＝10，
∴平行四边形DEFB的周长为2（DE＋BD）＝28.
1.连接三角形两边中点的线段，叫做的中位线.
2.三角形中位线定理 三角形的中位线平行于第三边，且等于第三边的一半 .
3.以任意四边形各边中点为顶点的四边形是平行四边形.
4.过三角形一边的中点，平行于另一边的直线必然平分第三边.
感谢收看