北师大八下6.4.1多边形的内角和与外角和(1)
文档属性
| 名称 | 北师大八下6.4.1多边形的内角和与外角和(1) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 14:23:10 | ||
图片预览




文档简介
(共27张PPT)
第六章 平行四边形
6.4.1多边形的内角和与外角和(1)
北师大版 数学 八年级 下册
学习目标
1.经历探索多边形内角和的过程,掌握多边形内角和公式.
2.灵活运用公式进行内角和的计算 ,并且会计算正多边形的一个内角的度数.
情景导入
1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
2:你知道长方形和正方形的内角和是多少吗?其他四边形的内角和是多少?
(都是360°)
3: 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
(n-3)
(n-2)
4:n边形的对角线一共有 条.
情景导入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?
本节课我们就来学习如何求多边形的内角和.
核心知识点一:
多边形的内角和
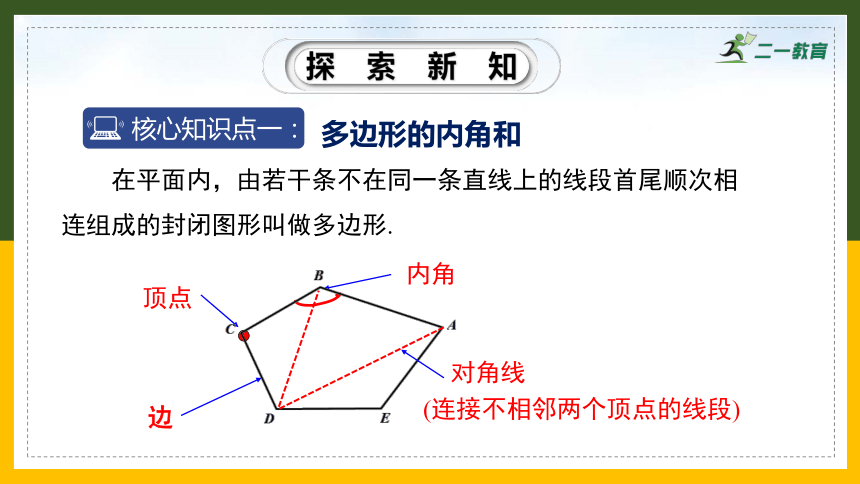
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
探索新知
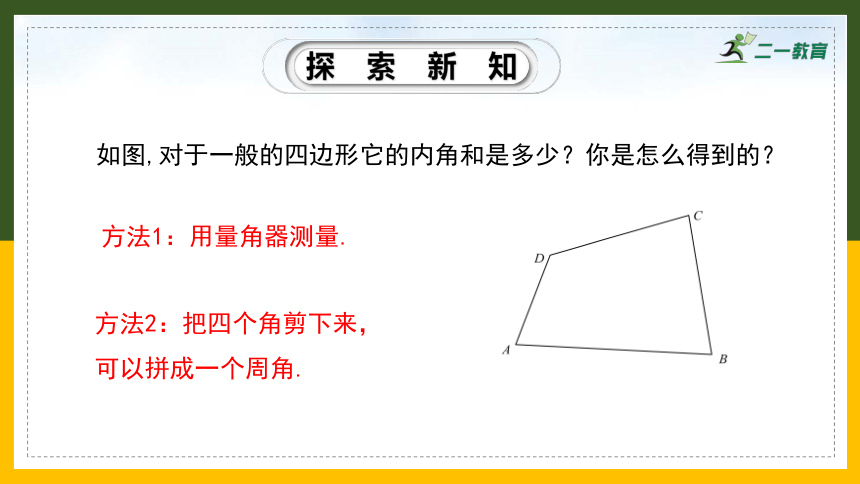
如图,对于一般的四边形它的内角和是多少?你是怎么得到的?
方法2:把四个角剪下来,
可以拼成一个周角.
方法1:用量角器测量.
探索新知
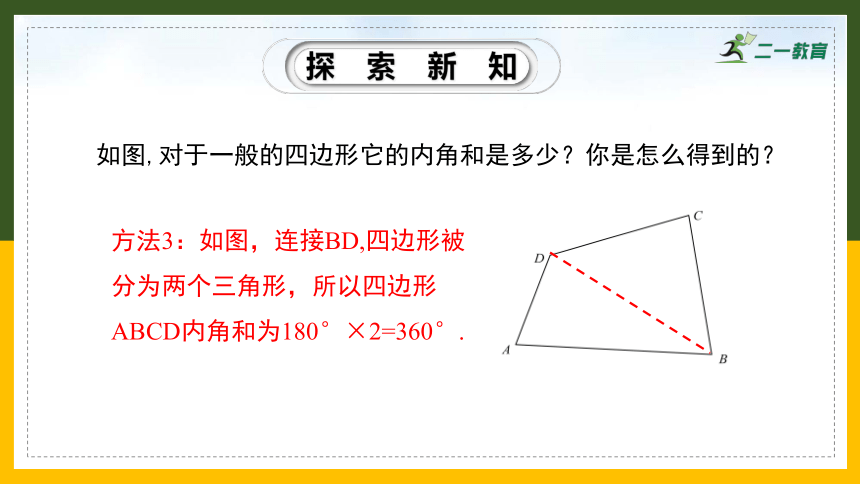
方法3:如图,连接BD,四边形被分为两个三角形,所以四边形ABCD内角和为180°×2=360°.
如图,对于一般的四边形它的内角和是多少?你是怎么得到的?
探索新知
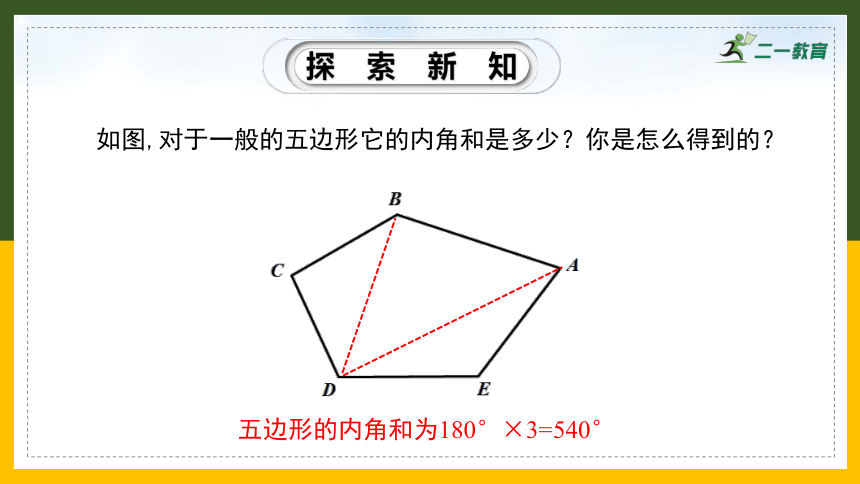
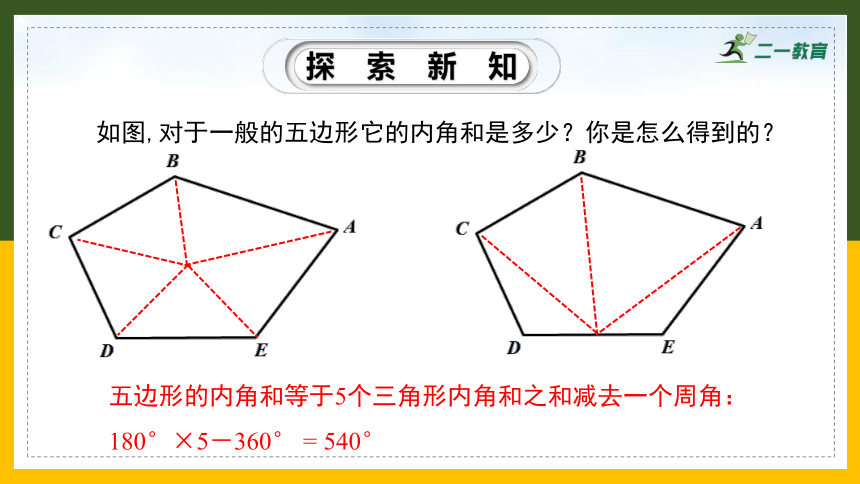
如图,对于一般的五边形它的内角和是多少?你是怎么得到的?
五边形的内角和为180°×3=540°
探索新知
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
如图,对于一般的五边形它的内角和是多少?你是怎么得到的?
探索新知
议一议 明晰结论
(1)五边形可以分割成三个三角形来算.
(2)五边形可以分割成五个三角形来计算.
(3)五边形可以分割成一个三角形和一个四边形来计算.
(4)n边形可以分割成(n-2)个三角形来计算.
探索新知
归纳总结
……
多边形边数 从一个顶点引出的对角线条数 分割成的三角形个数 多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
探索新知
多边形内角和定理:
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
归纳总结
探索新知
例:一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
探索新知
多边形内角和的三点注意
(1)多边形的内角和是指n个内角的度数之和.
(2)多边形的内角和为(n-2)·180°,且内角和为180°的整数倍.
(3)由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
归纳总结
探索新知
核心知识点二:
认识正多边形
观察图中的多边形,它们的边、角有什么特点?
正多边形定义:在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
探索新知
你能求出下列正多边形的每个内角吗?
图形 正多边形 内角和 每个内角
正三角形
正四边形
正五边形
正六边形
正n边形
…
180°
180°(n-2)
360°
540°
720°
90°
60°
120°
108°
180° (n-2)
n
探索新知
归纳总结
正n边形的每个内角度数为:
探索新知
当堂检测
1.以下角度是多边形的内角和的是( )
A.1 900° B.1 800°
C.560° D.270°
2.如图,在四边形ABCD中,∠A=60°,若沿图中虚线截去∠A,则∠1+∠2的和为( )
A.260° B.240°
C.200° D.120°
B
B
当堂检测
3.如图,如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )
A.30° B.15°
C.18° D.20°
C
当堂检测
4.七边形的内角和为( )
A.360° B.540°
C.720° D.900°
5.内角和为720°的多边形是( )
D
D
当堂检测
6.若一个多边形内角和等于1 260°,则该多边形边数是( )
A.8 B.9
C.10 D.11
7.下列角度中,不能成为多边形内角和的是( )
A.540° B.760°
C.900° D.1 080°
B
B
当堂检测
8.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是______度.
540
9.如图所示,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为_____.
9
当堂检测
10.如图,在五边形ABCDE中,∠C=90°,∠D=70°,∠E=130°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解:五边形ABCDE的内角和为(5-2) 180°=540°,
又∵∠C=90°,∠D=70°,∠E=130°,
∴∠EAB+∠ABC=250°.
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB+∠PBA=125°,
∴∠P=180°-125°=55°.
当堂检测
11.若一个n边形的内角和比它的外角和的3倍多180°,
(1)求n的值;
解:(1)设这个多边形的边数为n,则内角和为180°(n-2),
依题意得:
180°(n-2)=360°×3+180°,解得n=9,
答:n=9.
当堂检测
11.若一个n边形的内角和比它的外角和的3倍多180°,
(2)在(1)的条件下,求正(n+1)边形的一个内角度数及对角线条数.
解:(2)由(1)可知,n+1=10.
所以正十边形的一个内角为(10-2)×180°÷10=144°.
从n边形的一个顶点引出对角线,可以引(n-3)条,
则从十边形的一个顶点引出对角线,可以引7条,
所以一共有10×7÷2=35条.
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
正多
边形
内角=
感谢收看
第六章 平行四边形
6.4.1多边形的内角和与外角和(1)
北师大版 数学 八年级 下册
学习目标
1.经历探索多边形内角和的过程,掌握多边形内角和公式.
2.灵活运用公式进行内角和的计算 ,并且会计算正多边形的一个内角的度数.
情景导入
1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
2:你知道长方形和正方形的内角和是多少吗?其他四边形的内角和是多少?
(都是360°)
3: 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
(n-3)
(n-2)
4:n边形的对角线一共有 条.
情景导入
上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?
本节课我们就来学习如何求多边形的内角和.
核心知识点一:
多边形的内角和
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
探索新知
如图,对于一般的四边形它的内角和是多少?你是怎么得到的?
方法2:把四个角剪下来,
可以拼成一个周角.
方法1:用量角器测量.
探索新知
方法3:如图,连接BD,四边形被分为两个三角形,所以四边形ABCD内角和为180°×2=360°.
如图,对于一般的四边形它的内角和是多少?你是怎么得到的?
探索新知
如图,对于一般的五边形它的内角和是多少?你是怎么得到的?
五边形的内角和为180°×3=540°
探索新知
五边形的内角和等于5个三角形内角和之和减去一个周角:
180°×5-360° = 540°
如图,对于一般的五边形它的内角和是多少?你是怎么得到的?
探索新知
议一议 明晰结论
(1)五边形可以分割成三个三角形来算.
(2)五边形可以分割成五个三角形来计算.
(3)五边形可以分割成一个三角形和一个四边形来计算.
(4)n边形可以分割成(n-2)个三角形来计算.
探索新知
归纳总结
……
多边形边数 从一个顶点引出的对角线条数 分割成的三角形个数 多边形内角和
三角形(n=3)
四边形(n=4)
五边形(n=5)
六边形(n=6)
……
n边形
0
1
180°
1
2
360°
2
3
540°
3
4
720°
n-3
n-2
(n-2)·180°
探索新知
多边形内角和定理:
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
归纳总结
探索新知
例:一个多边形的内角和为1440°,则它是几边形?
解:设这个多边形是n边形,则
180°·(n-2)=1440°
∴ n=10
∴ 这个多边形是10边形
探索新知
多边形内角和的三点注意
(1)多边形的内角和是指n个内角的度数之和.
(2)多边形的内角和为(n-2)·180°,且内角和为180°的整数倍.
(3)由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
归纳总结
探索新知
核心知识点二:
认识正多边形
观察图中的多边形,它们的边、角有什么特点?
正多边形定义:在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
探索新知
你能求出下列正多边形的每个内角吗?
图形 正多边形 内角和 每个内角
正三角形
正四边形
正五边形
正六边形
正n边形
…
180°
180°(n-2)
360°
540°
720°
90°
60°
120°
108°
180° (n-2)
n
探索新知
归纳总结
正n边形的每个内角度数为:
探索新知
当堂检测
1.以下角度是多边形的内角和的是( )
A.1 900° B.1 800°
C.560° D.270°
2.如图,在四边形ABCD中,∠A=60°,若沿图中虚线截去∠A,则∠1+∠2的和为( )
A.260° B.240°
C.200° D.120°
B
B
当堂检测
3.如图,如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )
A.30° B.15°
C.18° D.20°
C
当堂检测
4.七边形的内角和为( )
A.360° B.540°
C.720° D.900°
5.内角和为720°的多边形是( )
D
D
当堂检测
6.若一个多边形内角和等于1 260°,则该多边形边数是( )
A.8 B.9
C.10 D.11
7.下列角度中,不能成为多边形内角和的是( )
A.540° B.760°
C.900° D.1 080°
B
B
当堂检测
8.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是______度.
540
9.如图所示,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为_____.
9
当堂检测
10.如图,在五边形ABCDE中,∠C=90°,∠D=70°,∠E=130°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
解:五边形ABCDE的内角和为(5-2) 180°=540°,
又∵∠C=90°,∠D=70°,∠E=130°,
∴∠EAB+∠ABC=250°.
∵AP平分∠EAB,BP平分∠ABC,
∴∠PAB+∠PBA=125°,
∴∠P=180°-125°=55°.
当堂检测
11.若一个n边形的内角和比它的外角和的3倍多180°,
(1)求n的值;
解:(1)设这个多边形的边数为n,则内角和为180°(n-2),
依题意得:
180°(n-2)=360°×3+180°,解得n=9,
答:n=9.
当堂检测
11.若一个n边形的内角和比它的外角和的3倍多180°,
(2)在(1)的条件下,求正(n+1)边形的一个内角度数及对角线条数.
解:(2)由(1)可知,n+1=10.
所以正十边形的一个内角为(10-2)×180°÷10=144°.
从n边形的一个顶点引出对角线,可以引(n-3)条,
则从十边形的一个顶点引出对角线,可以引7条,
所以一共有10×7÷2=35条.
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
正多
边形
内角=
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
