湖南省永州市祁阳县羊角塘镇中心学校2024-2025学年八年级下学期期中检测数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳县羊角塘镇中心学校2024-2025学年八年级下学期期中检测数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 914.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 00:00:00 | ||
图片预览



文档简介
祁阳市羊角塘镇中心学校2025年上期期中检测八年级下册《数学》试卷
一.选择题(共10小题,满分27分)
1.公元2025年是我国农历乙已年,属蛇年,春节期间,大小媒体会呈现大量以蛇为主题的文案,金蛇献瑞、蛇舞新春!下列年画图案中,是中心对称图形的是( )
A.B. C. D.
2.下列满足条件的三角形中,不是直角三角形的是( )
A.三内角的度数之比为3:4:5 B.在△ABC中,a2﹣b2=c2
C.三边长的平方之比为1:2:3
D.三边长分别为a,b,c,且a=n2﹣1,b=2n,c=n2+1(n>1)
3.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
4.矩形具备的性质是( )
A.对角线相等 B.对角线互相垂直
C.邻边相等 D.对角线平分一组对角
5.如图, ABCD中,对角线AC,BD相交于点O,点E是CD的中点,若BC=8,则OE的长为( )
A.6 B.5 C.4 D.3
6.如图,在四边形ABCD中,∠B=90°,AC=10,AB∥CD,AC平分∠DAB.AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A. B. C. D.
7.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为( )
A.5 B.7 C.8 D.
第5题图 第7题图 第8题图 第9题图
8.如图,△ABC中,AB=8cm,AC=6cm,点E是BC的中点,若AD平分∠BAC,CD⊥AD,线段DE的长为( )
A.1cm B.2cm C.3cm D.4cm
9.如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD交于点O.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“∠BAD=90°”,则四边形ABCD是矩形
B.添加“AB∥CD”,则四边形ABCD是菱形
C.添加“OA=OC”,则四边形ABCD是菱形
D.添加“∠ABC=∠BCD=90°”,则四边形ABCD是正方形
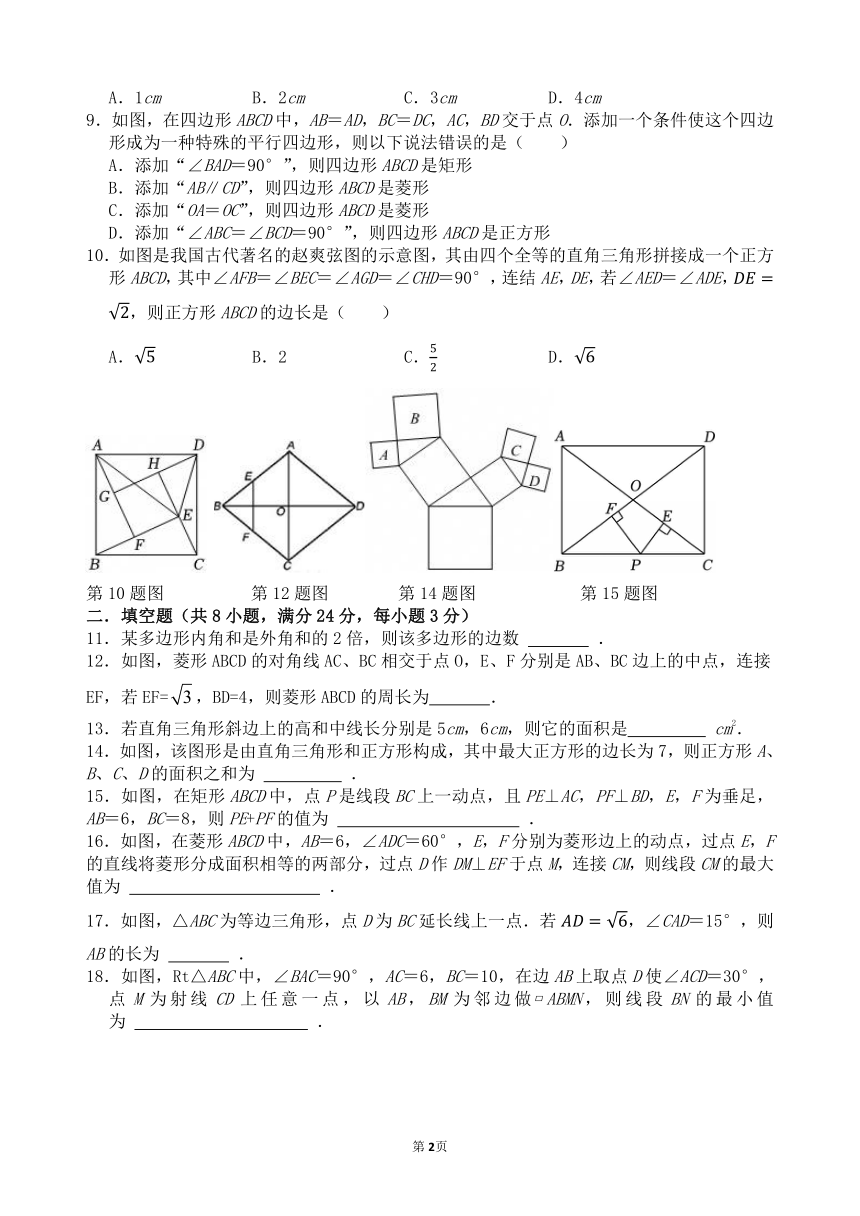
10.如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,其中∠AFB=∠BEC=∠AGD=∠CHD=90°,连结AE,DE,若∠AED=∠ADE,,则正方形ABCD的边长是( )
A. B.2 C. D.
第10题图 第12题图 第14题图 第15题图
二.填空题(共8小题,满分24分,每小题3分)
11.某多边形内角和是外角和的2倍,则该多边形的边数 .
12.如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF,若EF=,BD=4,则菱形ABCD的周长为 .
13.若直角三角形斜边上的高和中线长分别是5cm,6cm,则它的面积是 cm2.
14.如图,该图形是由直角三角形和正方形构成,其中最大正方形的边长为7,则正方形A、B、C、D的面积之和为 .
15.如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,E,F为垂足,AB=6,BC=8,则PE+PF的值为 .
16.如图,在菱形ABCD中,AB=6,∠ADC=60°,E,F分别为菱形边上的动点,过点E,F的直线将菱形分成面积相等的两部分,过点D作DM⊥EF于点M,连接CM,则线段CM的最大值为 .
17.如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 .
18.如图,Rt△ABC中,∠BAC=90°,AC=6,BC=10,在边AB上取点D使∠ACD=30°,点M为射线CD上任意一点,以AB,BM为邻边做 ABMN,则线段BN的最小值为 .
第16题图 第17题图 第18题图
三.解答题(共8小题,满分66分)
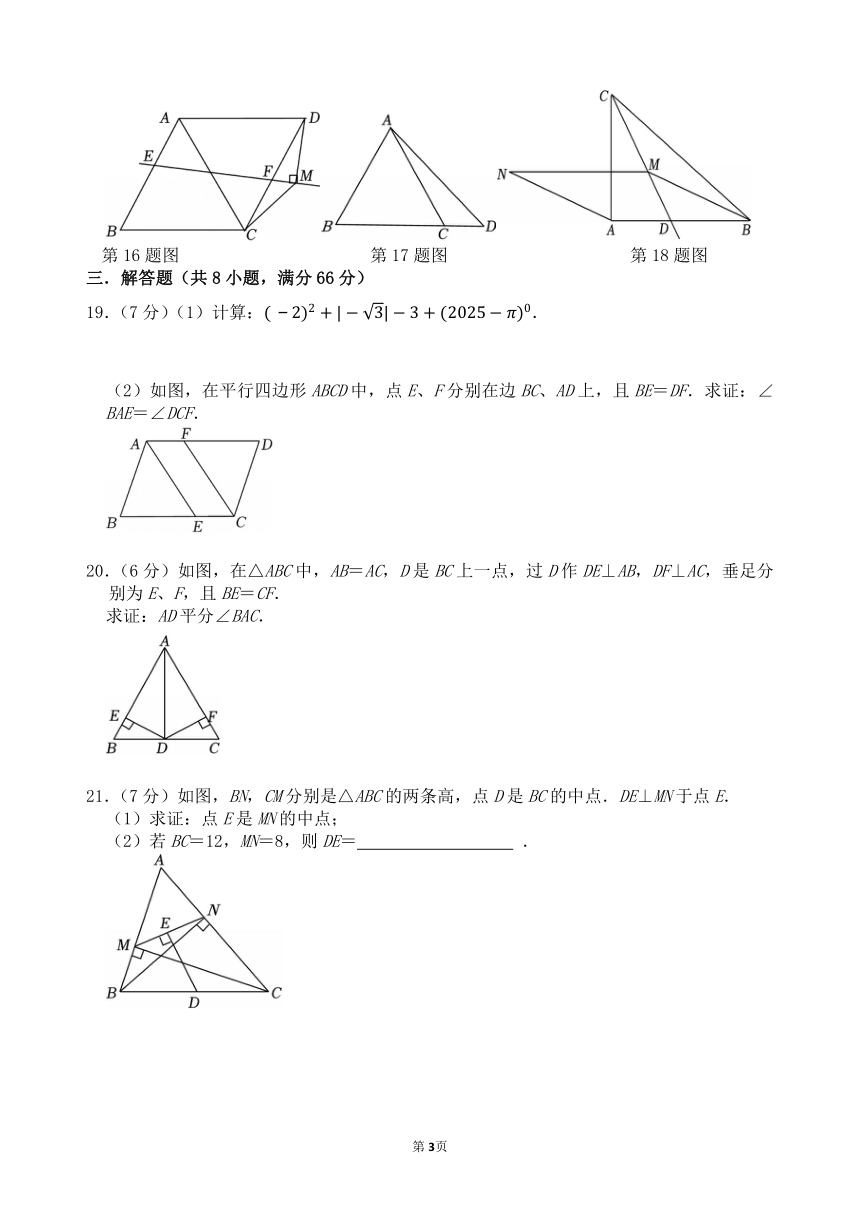
19.(7分)(1)计算:.
(2)如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,且BE=DF.求证:∠BAE=∠DCF.
20.(6分)如图,在△ABC中,AB=AC,D是BC上一点,过D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.
求证:AD平分∠BAC.
21.(7分)如图,BN,CM分别是△ABC的两条高,点D是BC的中点.DE⊥MN于点E.
(1)求证:点E是MN的中点;
(2)若BC=12,MN=8,则DE= .
22.(8分)在平行四边形ABCD中,对角线AC,BD交于点O,E为OA的中点,作OF∥AB,交BE延长于点F,连接AF.
(1)求证:△AEB≌△OEF;
(2)连接DF,当∠BAD= °时,四边形AODF是菱形.
23.(10分)如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(﹣3,4).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与y轴、x轴分别交于点D、F.
(1)BO= ;
(2)求点D的坐标;
(3)若点M在x轴上,则在直线BD上是否存在点N,使得以M、N、A、D为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
24.(8分)如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=10,CD=24,∠ABD=30°,∠BDC=120°,求EF的长.
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
25.(10分)如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点.
(1)求证:△ABE≌△DCE;
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与BC有什么数量关系?请说明理由.
26.(10分)小明学习了特殊的四边形后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是 .
(2)性质探究:通过探究,直接写出垂美四边形ABCD的面积S与两条对角线AC、BD之间的数量关系: .
(3)问题解决:如图2,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BG、CE交于点N,CE交AB于点M,连结GE.
①求证:四边形BCGE为垂美四边形;
②已知AC=4,AB=5,则四边形BCGE的面积为 .
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A C D B A A A
7.解析:如图,过C作CH⊥AB,连接DH;因ABCD是菱形,∠B=60°,可判定△ABC为等边三角形;所以AH=HB=4;再由BP=3,可得HP=1.要使CA′的长度最小,则梯形APQD沿直线PQ折叠后A的对应点A′应落在CH上,且对称轴PQ应满足PQ∥DH;由作图知,DHPQ为平行四边形,可得DQ=HP= 1,CQ=CD-DQ=8-1=7.
8.解析:如图,延长CD交AB于F,
∵AD平分∠BAC,∴∠CAD=∠FAD,∵CD⊥AD,∴∠ADC=∠ADF=90°,在△ADF和△ADC中,,
∴△ADF≌△ADC(ASA),
∴AF=AC,CD=FD,
∴BF=AB﹣AF=8﹣6=2cm,
又∵点E为BC的中点,∴DE是△BCF的中位线,∴.
9.解析:当添加“∠BAD=90°”,无法证明四边形ABCD是矩形,故选项A符合题意;
∵AB=AD,BC=DC,
∴AC垂直平分BD,
当添加:“AB∥CD”,则∠ABD=∠BDC,
∵∠BDC=∠DBC,
∴∠ABO=∠CBO,
又∵BO=BO,∠BOA=∠BOC,
∴△ABO≌△CBO(ASA),
∴BA=BC,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形,故选项B不符合题意;
当添加条件“OA=OC”时,
∵OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故选项C不符合题意;
当添加条件“∠ABC=∠BCD=90°”时,则∠ABC+∠BCD=180°,∴AB∥CD,
由证选项A可知四边形ABCD是菱形,∵∠ABC=90°,
∴四边形ABCD是正方形,故选项D不符合题意;
10.解析:∵四边形ABCD是正方形,
∴AB=AD,
∵∠AED=∠ADE,
∴AE=AD,
∴AB=AE,
∵∠AFB=90°,
∴AF⊥BE,
∴EF=BF,
∵由四个全等的直角三角形拼接成一个正方形ABCD,
∴BE=CH,EF=BF=DH=CE,
∴EF=BE﹣BF=CH﹣CE=EH,
∴EH=DH=CE,
∵∠CHD=90°,DE,
∴DEDH,
∴EH=DH=CE=1,
∴CH=2EH=2,
∴CD,
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
11.6.
12.
13.30.
14.49.
15..
16..解析:如图,连接BD交AC于点O.取OD的中点T,连接TM,TC,
∵直线EF将菱形分成面积相等的两部分,
∴直线EF经过点O,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=6,∠ADC=∠ABC=60°,AC⊥BD,OA=OC,OB=OD,
∴△ABC,△ADC都是等边三角形,
∴AC=AB=6,OA=OC=3,
,
∵,
∴,
∵D M⊥E F,∴∠DMO=90°,∵O T=T D,∴,∴,∴CM的最大值为.
17.2.解析:过点A作AE⊥BC于点E,
∵△ABC是等边三角形,
∴BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,
∴∠BAE=∠CAE=30°,
∵∠CAD=15°,
∴∠EAD=∠CAE+∠CAD=30°+15°=45°,
∴△AED是等腰直角三角形,
设CE=x,
∵∠CAE=30°,AE⊥BC,
∴AC=2CE=2x,
由勾股定理得,AE,
∴DE=AE,
由勾股定理得,AE2+DE2=AD2,
∴,
解得x=1,
∴AC=2x=2,
∴AB=AC=2,
18..解析:连接BN,AM,BN与AM交于点O,取AC的中点E,AD的中点F,作射线EF,过点B作BH⊥EF,垂足为H,如图所示:
在平行四边形ABMN中,OB=ON,AO=MO,
∵点M为射线CD上任意一点,
∴点O在射线EF上,
当OB取得最小值时,BN取得最小值,
即当点O与点H重合时,BN取得最小值,
此时BN=2BH,
∵∠ACD=30°,∠BAC=90°,AC=6,
设AD=x,
则CD=2x,
根据勾股定理,得x2+62=(2x)2,
解得x,
∴AD,
∵E为AC的中点,F为AD的中点,
∴EF为△ADC的中位线,AF,
∴EF∥CD,
∴∠AEF=∠ACD=30°,
∴∠AFE=60°,
∴∠BFH=∠AFE=60°,
∵∠BHF=90°,
∴∠HBF=30°,
∵AC=6,BC=10,∠BAC=90°,
根据勾股定理,得AB8,
∴BF=8,
∴FH,
在Rt△FHB中,根据勾股定理,得BH,
∴BN的最小值为2,
三.解答题(共8小题,满分66分)
19.解:(1)原式=431=2+;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,
在△BAE与△DCF中,
,
∴△BAE≌△DCF(SAS),
∴∠BAE=∠DCF.
20.证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
21.(1)证明:如图,连接DM,DN.∵BN,CM分别是△ABC的两条高,
∴∠BMC=∠CNB=90°.
∵D是BC的中点,
∴,.
∴DM=DN.
∵DE⊥MN,
∴点E是MN的中点.
(2)解;∵BC=12,
∴,
∵点E是MN的中点,MN=8,
∴,
在Rt△DEN,由勾股定理得DN2=DE2+EN2,
∴.
故答案为:2.
22.(1)证明:∵AB∥OF,
∴∠ABF=∠OFB,
∵E为OA的中点,
∴AE=OE,
在△AEB与△OEF中,
,
∴△AEB≌△OEF(AAS),
(2)解:若∠BAD=90°,则四边形AODF是菱形,
证明:在 ABCD中,∠BAD=90°,
∴四边形ABCD是矩形,
∴AC=BD,AOAC,ODBD,
∴AO=OD,
∵△AEB≌△OEF,
∴AB=OF,
∵AB∥OF,
∴四边形ABOF是平行四边形,
∴AF∥OB,AF=OB,
∴AF=OD,
∴四边形AODF是平行四边形,
∵AO=OD,
∴四边形AODF是菱形.
故答案为:90.
23.解:(1)由B(﹣3,4)可得OC=3,BC=4.
∵四边形ABCO是矩形,
∴∠BCO=90°,
由勾股定理可得:BO5,
故答案为:5;
(2)设D(0,t),则由题意可得:∠DEO=90°,DE=DA=4﹣t,BE=BA=3,EO=2.
在Rt△DEO中,由勾股定理可得:OE2+DE2=DO2,
即22+(4﹣t)2=t2,
解得t,
∴D(0,);
(3)存在符合条件的点N(2,)或(8,)或(﹣8,).理由如下:
由(2)知:DE=DA=4﹣b,b,
∴AD=4,
设直线BD的解析式为y=kx+b,
∵B(﹣3,4),D(0,),
∴,
∴,
∴直线BD的解析式为:yx,
∵点M在x轴上,点N在直线BD上,
∴设M(m,0),N(n,n),
又A(0,4),D(0,),
当AM、DN为 ADMN的对角线时,AM与DN的中点重合,
∴,
解得:
∴N(2,);
当AN、DM为 ADNM的对角线时,AN与DM的中点重合,
∴,
解得:,
∴N(8,);
当AD、MN为 AMDN的对角线时,AD与MN的中点重合,
∴,
解得:,
∴N(﹣8,);
∴N(2,)或(8,)或(﹣8,).
24.(1)解:如图,取BD的中点P,连接EP、FP,
∵E,F分别是AD、BC的中点,AB=10,CD=24,
∴PE是△ABD的中位线,PF是△BCD的中位线,
∴PE∥AB,且,且,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=180°﹣120°=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在Rt△EPF中,由勾股定理得:,
即EF的长为13;
(2)证明:由(1)可知,PE是△ABD的中位线,PF是△BCD的中位线,
∴PE∥AB,且,PF∥CD,且,
∴∠EPD=∠ABD,∠DPF=180°﹣∠BDC.
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴,
∴AB2+CD2=4EF2.
25.25.(1)证明:由题意可得ABCD是等腰梯形,∴∠A=∠D,
在△ABE和△DCE中,AE=ED,∠A=∠D, AB=DC,∴△ABE≌△DCE.
(2)四边形EGFH是菱形.证明:∵GF、FH是△EBC的中位线,且由(1)得EB=EC,
∴GF∥EH,GE∥HF,GF=GE,∴四边形EGFH是菱形.
(3)EF⊥BC,且EF=BC.证明:连接EF,∵EFGH是正方形,
∴∠GEH=90°,即△BEC是等腰直角三角形,∴EF⊥BC,且EF=BC.
26.(1)解:∵在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,∴菱形和正方形一定是垂美四边形;故答案为:菱形、正方形;
(2)解:如图1所示:
∵四边形ABCD的面积=△ABC的面积+△ADC的面积AC BOAC DOAC BD;
故答案为:AC BD;
(3)①证明:连接CG、BE,如图2所示:
∵四边形ACFG和四边形ABDE是正方形,∴∠F=∠CAG=∠BAE=90°,FG=AG=AC=CF,AB=AE,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,
∴△GAB≌△CAE (SAS),∴BG=CE,∠ABG=∠AEC,∵∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG十∠BMN=90°,∴∠BNM=90°,∴BG⊥CE,∴四边形BCGE为垂美四边形;②解:∵FG=CF=AC=4,∠ACB=90°,AB=5,
∴BC3,∴BF=BC+CF=7,在Rt△BFG中,
BG,∴CE=BG,∵四边形BCGE为垂美四边形,
∴四边形BCGE的面积BG CE,
第15页
一.选择题(共10小题,满分27分)
1.公元2025年是我国农历乙已年,属蛇年,春节期间,大小媒体会呈现大量以蛇为主题的文案,金蛇献瑞、蛇舞新春!下列年画图案中,是中心对称图形的是( )
A.B. C. D.
2.下列满足条件的三角形中,不是直角三角形的是( )
A.三内角的度数之比为3:4:5 B.在△ABC中,a2﹣b2=c2
C.三边长的平方之比为1:2:3
D.三边长分别为a,b,c,且a=n2﹣1,b=2n,c=n2+1(n>1)
3.在如图所示的图形中,属于多边形的有( )
A.2个 B.3个 C.4个 D.5个
4.矩形具备的性质是( )
A.对角线相等 B.对角线互相垂直
C.邻边相等 D.对角线平分一组对角
5.如图, ABCD中,对角线AC,BD相交于点O,点E是CD的中点,若BC=8,则OE的长为( )
A.6 B.5 C.4 D.3
6.如图,在四边形ABCD中,∠B=90°,AC=10,AB∥CD,AC平分∠DAB.AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A. B. C. D.
7.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为( )
A.5 B.7 C.8 D.
第5题图 第7题图 第8题图 第9题图
8.如图,△ABC中,AB=8cm,AC=6cm,点E是BC的中点,若AD平分∠BAC,CD⊥AD,线段DE的长为( )
A.1cm B.2cm C.3cm D.4cm
9.如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD交于点O.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“∠BAD=90°”,则四边形ABCD是矩形
B.添加“AB∥CD”,则四边形ABCD是菱形
C.添加“OA=OC”,则四边形ABCD是菱形
D.添加“∠ABC=∠BCD=90°”,则四边形ABCD是正方形
10.如图是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,其中∠AFB=∠BEC=∠AGD=∠CHD=90°,连结AE,DE,若∠AED=∠ADE,,则正方形ABCD的边长是( )
A. B.2 C. D.
第10题图 第12题图 第14题图 第15题图
二.填空题(共8小题,满分24分,每小题3分)
11.某多边形内角和是外角和的2倍,则该多边形的边数 .
12.如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF,若EF=,BD=4,则菱形ABCD的周长为 .
13.若直角三角形斜边上的高和中线长分别是5cm,6cm,则它的面积是 cm2.
14.如图,该图形是由直角三角形和正方形构成,其中最大正方形的边长为7,则正方形A、B、C、D的面积之和为 .
15.如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,E,F为垂足,AB=6,BC=8,则PE+PF的值为 .
16.如图,在菱形ABCD中,AB=6,∠ADC=60°,E,F分别为菱形边上的动点,过点E,F的直线将菱形分成面积相等的两部分,过点D作DM⊥EF于点M,连接CM,则线段CM的最大值为 .
17.如图,△ABC为等边三角形,点D为BC延长线上一点.若,∠CAD=15°,则AB的长为 .
18.如图,Rt△ABC中,∠BAC=90°,AC=6,BC=10,在边AB上取点D使∠ACD=30°,点M为射线CD上任意一点,以AB,BM为邻边做 ABMN,则线段BN的最小值为 .
第16题图 第17题图 第18题图
三.解答题(共8小题,满分66分)
19.(7分)(1)计算:.
(2)如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,且BE=DF.求证:∠BAE=∠DCF.
20.(6分)如图,在△ABC中,AB=AC,D是BC上一点,过D作DE⊥AB,DF⊥AC,垂足分别为E、F,且BE=CF.
求证:AD平分∠BAC.
21.(7分)如图,BN,CM分别是△ABC的两条高,点D是BC的中点.DE⊥MN于点E.
(1)求证:点E是MN的中点;
(2)若BC=12,MN=8,则DE= .
22.(8分)在平行四边形ABCD中,对角线AC,BD交于点O,E为OA的中点,作OF∥AB,交BE延长于点F,连接AF.
(1)求证:△AEB≌△OEF;
(2)连接DF,当∠BAD= °时,四边形AODF是菱形.
23.(10分)如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(﹣3,4).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与y轴、x轴分别交于点D、F.
(1)BO= ;
(2)求点D的坐标;
(3)若点M在x轴上,则在直线BD上是否存在点N,使得以M、N、A、D为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
24.(8分)如图,在四边形ABCD中,E,F分别是AD,BC的中点.
(1)若AB=10,CD=24,∠ABD=30°,∠BDC=120°,求EF的长.
(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.
25.(10分)如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点.
(1)求证:△ABE≌△DCE;
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与BC有什么数量关系?请说明理由.
26.(10分)小明学习了特殊的四边形后,对特殊四边形的探究产生了兴趣,发现另外一类特殊四边形,如图1,我们把两条对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是 .
(2)性质探究:通过探究,直接写出垂美四边形ABCD的面积S与两条对角线AC、BD之间的数量关系: .
(3)问题解决:如图2,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BG、CE交于点N,CE交AB于点M,连结GE.
①求证:四边形BCGE为垂美四边形;
②已知AC=4,AB=5,则四边形BCGE的面积为 .
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A C D B A A A
7.解析:如图,过C作CH⊥AB,连接DH;因ABCD是菱形,∠B=60°,可判定△ABC为等边三角形;所以AH=HB=4;再由BP=3,可得HP=1.要使CA′的长度最小,则梯形APQD沿直线PQ折叠后A的对应点A′应落在CH上,且对称轴PQ应满足PQ∥DH;由作图知,DHPQ为平行四边形,可得DQ=HP= 1,CQ=CD-DQ=8-1=7.
8.解析:如图,延长CD交AB于F,
∵AD平分∠BAC,∴∠CAD=∠FAD,∵CD⊥AD,∴∠ADC=∠ADF=90°,在△ADF和△ADC中,,
∴△ADF≌△ADC(ASA),
∴AF=AC,CD=FD,
∴BF=AB﹣AF=8﹣6=2cm,
又∵点E为BC的中点,∴DE是△BCF的中位线,∴.
9.解析:当添加“∠BAD=90°”,无法证明四边形ABCD是矩形,故选项A符合题意;
∵AB=AD,BC=DC,
∴AC垂直平分BD,
当添加:“AB∥CD”,则∠ABD=∠BDC,
∵∠BDC=∠DBC,
∴∠ABO=∠CBO,
又∵BO=BO,∠BOA=∠BOC,
∴△ABO≌△CBO(ASA),
∴BA=BC,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形,故选项B不符合题意;
当添加条件“OA=OC”时,
∵OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故选项C不符合题意;
当添加条件“∠ABC=∠BCD=90°”时,则∠ABC+∠BCD=180°,∴AB∥CD,
由证选项A可知四边形ABCD是菱形,∵∠ABC=90°,
∴四边形ABCD是正方形,故选项D不符合题意;
10.解析:∵四边形ABCD是正方形,
∴AB=AD,
∵∠AED=∠ADE,
∴AE=AD,
∴AB=AE,
∵∠AFB=90°,
∴AF⊥BE,
∴EF=BF,
∵由四个全等的直角三角形拼接成一个正方形ABCD,
∴BE=CH,EF=BF=DH=CE,
∴EF=BE﹣BF=CH﹣CE=EH,
∴EH=DH=CE,
∵∠CHD=90°,DE,
∴DEDH,
∴EH=DH=CE=1,
∴CH=2EH=2,
∴CD,
故选:A.
二.填空题(共8小题,满分24分,每小题3分)
11.6.
12.
13.30.
14.49.
15..
16..解析:如图,连接BD交AC于点O.取OD的中点T,连接TM,TC,
∵直线EF将菱形分成面积相等的两部分,
∴直线EF经过点O,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=6,∠ADC=∠ABC=60°,AC⊥BD,OA=OC,OB=OD,
∴△ABC,△ADC都是等边三角形,
∴AC=AB=6,OA=OC=3,
,
∵,
∴,
∵D M⊥E F,∴∠DMO=90°,∵O T=T D,∴,∴,∴CM的最大值为.
17.2.解析:过点A作AE⊥BC于点E,
∵△ABC是等边三角形,
∴BE=CE,∠BAE=∠CAE,∠BAC=60°,AB=AC,
∴∠BAE=∠CAE=30°,
∵∠CAD=15°,
∴∠EAD=∠CAE+∠CAD=30°+15°=45°,
∴△AED是等腰直角三角形,
设CE=x,
∵∠CAE=30°,AE⊥BC,
∴AC=2CE=2x,
由勾股定理得,AE,
∴DE=AE,
由勾股定理得,AE2+DE2=AD2,
∴,
解得x=1,
∴AC=2x=2,
∴AB=AC=2,
18..解析:连接BN,AM,BN与AM交于点O,取AC的中点E,AD的中点F,作射线EF,过点B作BH⊥EF,垂足为H,如图所示:
在平行四边形ABMN中,OB=ON,AO=MO,
∵点M为射线CD上任意一点,
∴点O在射线EF上,
当OB取得最小值时,BN取得最小值,
即当点O与点H重合时,BN取得最小值,
此时BN=2BH,
∵∠ACD=30°,∠BAC=90°,AC=6,
设AD=x,
则CD=2x,
根据勾股定理,得x2+62=(2x)2,
解得x,
∴AD,
∵E为AC的中点,F为AD的中点,
∴EF为△ADC的中位线,AF,
∴EF∥CD,
∴∠AEF=∠ACD=30°,
∴∠AFE=60°,
∴∠BFH=∠AFE=60°,
∵∠BHF=90°,
∴∠HBF=30°,
∵AC=6,BC=10,∠BAC=90°,
根据勾股定理,得AB8,
∴BF=8,
∴FH,
在Rt△FHB中,根据勾股定理,得BH,
∴BN的最小值为2,
三.解答题(共8小题,满分66分)
19.解:(1)原式=431=2+;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D,
在△BAE与△DCF中,
,
∴△BAE≌△DCF(SAS),
∴∠BAE=∠DCF.
20.证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
21.(1)证明:如图,连接DM,DN.∵BN,CM分别是△ABC的两条高,
∴∠BMC=∠CNB=90°.
∵D是BC的中点,
∴,.
∴DM=DN.
∵DE⊥MN,
∴点E是MN的中点.
(2)解;∵BC=12,
∴,
∵点E是MN的中点,MN=8,
∴,
在Rt△DEN,由勾股定理得DN2=DE2+EN2,
∴.
故答案为:2.
22.(1)证明:∵AB∥OF,
∴∠ABF=∠OFB,
∵E为OA的中点,
∴AE=OE,
在△AEB与△OEF中,
,
∴△AEB≌△OEF(AAS),
(2)解:若∠BAD=90°,则四边形AODF是菱形,
证明:在 ABCD中,∠BAD=90°,
∴四边形ABCD是矩形,
∴AC=BD,AOAC,ODBD,
∴AO=OD,
∵△AEB≌△OEF,
∴AB=OF,
∵AB∥OF,
∴四边形ABOF是平行四边形,
∴AF∥OB,AF=OB,
∴AF=OD,
∴四边形AODF是平行四边形,
∵AO=OD,
∴四边形AODF是菱形.
故答案为:90.
23.解:(1)由B(﹣3,4)可得OC=3,BC=4.
∵四边形ABCO是矩形,
∴∠BCO=90°,
由勾股定理可得:BO5,
故答案为:5;
(2)设D(0,t),则由题意可得:∠DEO=90°,DE=DA=4﹣t,BE=BA=3,EO=2.
在Rt△DEO中,由勾股定理可得:OE2+DE2=DO2,
即22+(4﹣t)2=t2,
解得t,
∴D(0,);
(3)存在符合条件的点N(2,)或(8,)或(﹣8,).理由如下:
由(2)知:DE=DA=4﹣b,b,
∴AD=4,
设直线BD的解析式为y=kx+b,
∵B(﹣3,4),D(0,),
∴,
∴,
∴直线BD的解析式为:yx,
∵点M在x轴上,点N在直线BD上,
∴设M(m,0),N(n,n),
又A(0,4),D(0,),
当AM、DN为 ADMN的对角线时,AM与DN的中点重合,
∴,
解得:
∴N(2,);
当AN、DM为 ADNM的对角线时,AN与DM的中点重合,
∴,
解得:,
∴N(8,);
当AD、MN为 AMDN的对角线时,AD与MN的中点重合,
∴,
解得:,
∴N(﹣8,);
∴N(2,)或(8,)或(﹣8,).
24.(1)解:如图,取BD的中点P,连接EP、FP,
∵E,F分别是AD、BC的中点,AB=10,CD=24,
∴PE是△ABD的中位线,PF是△BCD的中位线,
∴PE∥AB,且,且,
∴∠EPD=∠ABD=30°,∠DPF=180°﹣∠BDC=180°﹣120°=60°,
∴∠EPF=∠EPD+∠DPF=90°,
在Rt△EPF中,由勾股定理得:,
即EF的长为13;
(2)证明:由(1)可知,PE是△ABD的中位线,PF是△BCD的中位线,
∴PE∥AB,且,PF∥CD,且,
∴∠EPD=∠ABD,∠DPF=180°﹣∠BDC.
∵∠BDC﹣∠ABD=90°,
∴∠BDC=90°+∠ABD,
∴∠EPF=∠EPD+∠DPF=∠ABD+180°﹣∠BDC=∠ABD+180°﹣(90°+∠ABD)=90°,
∴,
∴AB2+CD2=4EF2.
25.25.(1)证明:由题意可得ABCD是等腰梯形,∴∠A=∠D,
在△ABE和△DCE中,AE=ED,∠A=∠D, AB=DC,∴△ABE≌△DCE.
(2)四边形EGFH是菱形.证明:∵GF、FH是△EBC的中位线,且由(1)得EB=EC,
∴GF∥EH,GE∥HF,GF=GE,∴四边形EGFH是菱形.
(3)EF⊥BC,且EF=BC.证明:连接EF,∵EFGH是正方形,
∴∠GEH=90°,即△BEC是等腰直角三角形,∴EF⊥BC,且EF=BC.
26.(1)解:∵在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,∴菱形和正方形一定是垂美四边形;故答案为:菱形、正方形;
(2)解:如图1所示:
∵四边形ABCD的面积=△ABC的面积+△ADC的面积AC BOAC DOAC BD;
故答案为:AC BD;
(3)①证明:连接CG、BE,如图2所示:
∵四边形ACFG和四边形ABDE是正方形,∴∠F=∠CAG=∠BAE=90°,FG=AG=AC=CF,AB=AE,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,
∴△GAB≌△CAE (SAS),∴BG=CE,∠ABG=∠AEC,∵∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG十∠BMN=90°,∴∠BNM=90°,∴BG⊥CE,∴四边形BCGE为垂美四边形;②解:∵FG=CF=AC=4,∠ACB=90°,AB=5,
∴BC3,∴BF=BC+CF=7,在Rt△BFG中,
BG,∴CE=BG,∵四边形BCGE为垂美四边形,
∴四边形BCGE的面积BG CE,
第15页
同课章节目录
