2024-2025学年人教版七年级下册月考(5月份)数学试卷(考试范围:第7~10章)(含解析)
文档属性
| 名称 | 2024-2025学年人教版七年级下册月考(5月份)数学试卷(考试范围:第7~10章)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 718.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 08:34:31 | ||
图片预览




文档简介
2024-2025学年七年级下册月考(5月份)数学试卷(考试范围:第7~10章)
一.选择题(共10小题,满分30分,每小题3分)
1.下列命题中,是真命题的是( )
A.相等的角是对顶角
B.同位角互补,两直线平行
C.同位角相等
D.在同一平面内,垂直于同一条直线的两条直线互相平行
2.下列实数:,其中最小的是( )
A. B.0 C. D.
3.若点的坐标满足条件,则点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.如果方程组的解为,那么被“”“”遮住的两个数分别是( )
A., B., C., D.,
5.如图是某运动员在一次山地自行车越野赛中经过的路线,已知第一次的拐角,第三次的拐角,若第三次拐弯后的道路恰好与第一次拐弯前的道路平行,则第二次的拐角的度数为( )
A. B. C. D.
6.在平面直角坐标系中,点与点关于x轴对称,则的值是( )
A. B.2 C. D.
7.若关于,的二元一次方程组的解也是二元一次方程的解,则的值为( )
A. B. C. D.
8.如图,在平面直角坐标系中,将线段平移后得到线段,点和点的对应点分别是点和点.若点,,,则点的坐标为( )
A. B. C. D.
9.在量子物理的研究中,科学家需要精确计算微观粒子的能量、已知某微观粒子的能量可以用公式表示.当,时,该微观粒子的能量的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.8和9之间
10.如图,,则与的数量关系是( )
A. B.
C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.一个正数的两个平方根分别是与,则这个正数是 .
12.如图,与是内错角的是 .
13.已知点和点,且平行于轴,则点坐标为 .
14.如图,已知,,平分,则 .
15.已知是方程组的解,则的值为 .
16.如图,平分,平分,的反向延长线交于点,若,则 .
三.解答题(共8小题,满分72分)
17.(6分)计算:
(1) (2)
18.(6分)解下列方程组:
(1) (2)
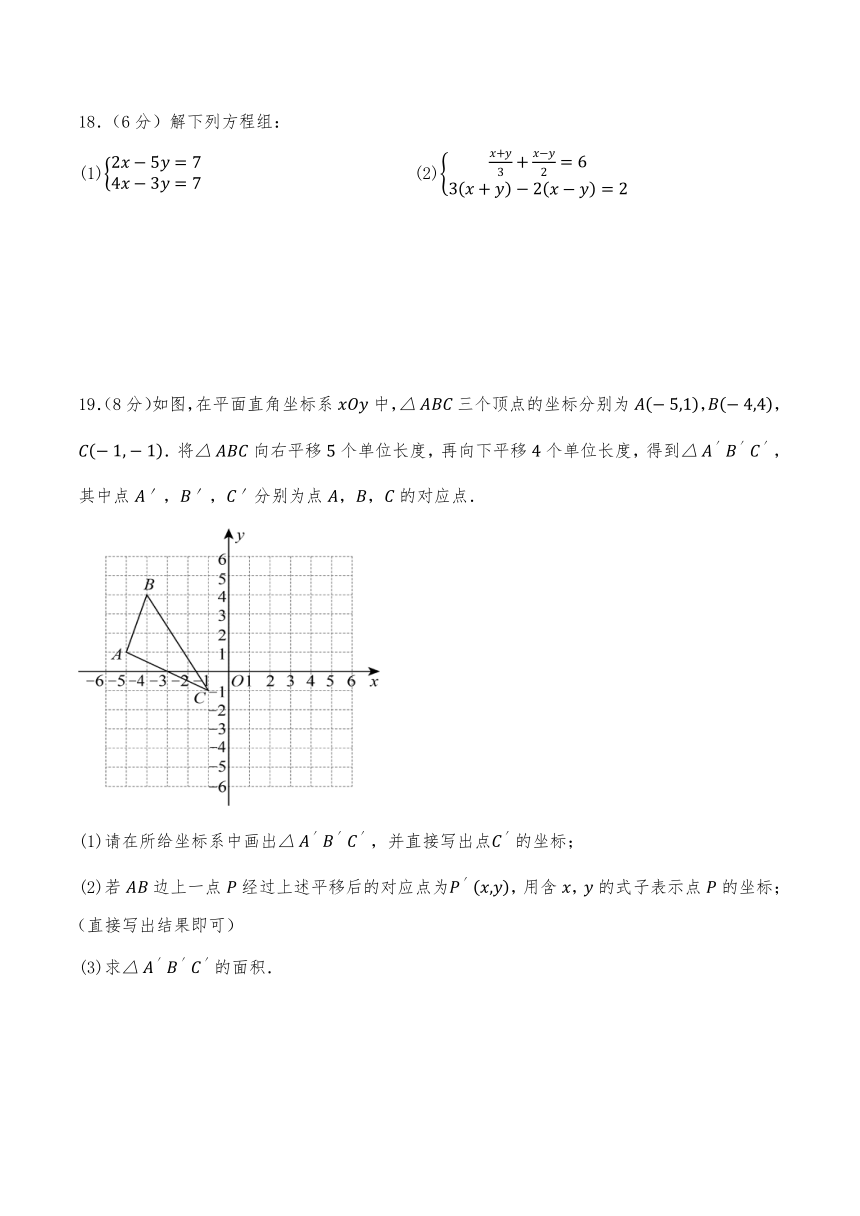
19.(8分)如图,在平面直角坐标系中,三个顶点的坐标分别为,,.将向右平移个单位长度,再向下平移个单位长度,得到,其中点,,分别为点,,的对应点.
(1)请在所给坐标系中画出,并直接写出点的坐标;
(2)若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标;(直接写出结果即可)
(3)求的面积.
20.(8分)如图,已知直线、相交于点O,,点O为垂足,平分.
(1)若,求的度数;
(2)若,求的度数.
21.(10分)已知一个数的两个平方根分别是和,的立方根为,c是的整数部分.
(1)求a,b,c的值.
(2)求的平方根.
22.(10分)读懂下面的推理过程,并填空 (理由或数学式).
中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图1是一个“互”字,如图2是由图1抽象出的几何图形,其中,点E,M,F在同一直线上,点G,H,N在同一条直线上,且,.求证:
证明:如图2,延长交于点 P.
∵(已知)
∴ ( )
又∵( 已知 ),
∴ (等量代换).
∴ ( ).
∴ (两直线平行,同旁内角互补).
又∵ (已知)
∴( )
∴( 同角的补角相等).
23.(12分)【背景】为了激励学习好的学生,班主任去奶茶店购买A、B两种款式的奶茶作为奖品.如图所示.
【素材1】若买3杯A款奶茶,2杯B款奶茶,共需54元;若买2杯A款奶茶,3杯B款奶茶,共需56元.
【素材2】为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完款式后可以自主选择加料一份或者不加料.
【任务1】求A款奶茶和B款奶茶的销售单价各是多少元?
【任务2】在不加料的情况下,购买A、B两种款式的奶茶(两种都要),刚好花220元,请问有几种购买方案?
【任务3】根据【素材2】小华恰好用了260元购买A、B两款奶茶,其中A款不加料的杯数是总杯数的.求B款加料的奶茶买了多少杯?
24.(12分)如图,已知是直线,间的一点,于点,交于点, .
(1) .
(2)如图2,射线从出发,以每秒的速度绕点按逆时针方向旋转,当垂直时,立刻按原速返回至后停止运动;射线从出发,以每秒的速度绕点按逆时针方向旋转至后停止运动,若射线,射线同时开始运动,设运动时间为秒.
①当时,请求出的度数;
②当时,请求出的值.
参考答案
一.选择题
1.D
【分析】本题考查了命题,根据对顶角的定义、平行线的判定和性质逐项判断即可求解,掌握以上知识点是解题的关键.
【详解】解:、相等的角不一定是对顶角,该选项命题是假命题,不合题意;
、同位角相等,两直线平行,该选项命题是假命题,不合题意;
、两直线平行,同位角相等,该选项命题是假命题,不合题意;
、在同一平面内,垂直于同一条直线的两条直线互相平行,该选项命题是真命题,符合题意;
故选:.
2.A
【分析】本题考查了实数的大小比较,根据实数的大小比较方法即可得出答案,掌握实数的大小比较方法是解题的关键.
【详解】解:∵,
∴最小的是,
故选:A.
3.D
【分析】本题考查了平方的非负性、绝对值的非负性、平面直角坐标系中点的坐标.首先根据平方的非负性和绝对值的非负性得到,,从而可得点的坐标为,根据坐标判断点所在原象限.
【详解】解:
又,,
,,
解得:,,
点的坐标为,
点在第四象限.
故选:D.
4.A
【分析】本题考查二元一次方程组的解,把代入先求出,再代入求出.解题的关键是理解方程组解的定义.
【详解】解:∵方程组的解为,
∴分别为方程和的解,
∴,
∴,
∴,
∴,
∴被“”“”遮住的两个数分别是,.
故选:A.
5.A
【分析】本题考查了平行线的判定与性质,过点作直线,根据平行线的性质得到,再得到,得出,即可求解,掌握相关知识是解题的关键.
【详解】解:如解图,过点作直线,
∴,
∵,且,
∴,
∴,
∵,
∴,
∴,
故选:A.
6.D
【分析】本题考查关于x轴对称的点的坐标,立方根,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数,可得m、n的值,再求的立方根即可.
【详解】解:点与点关于x轴对称,
,,
,,
,
故选D.
7.B
【分析】本题考查了解二元一次方程组和解一元一次方程,先解方程组,用含k的代数式表示x、y,再把x、y的值代入二元一次方程中,求出k.
【详解】解:,
,得,
∴,
,得,
∴,
∵二元一次方程组的解也是二元一次方程的解,
∴,
即,
∴.
故选:B.
8.D
【分析】本题考查了平移与坐标,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.根据点、的坐标确定出平移方式,再根据平移方式结合图形解答即可.
【详解】解:点的对应点,
平移规律为向右平移个单位,再向上平移个单位,
向右平移个单位,再向上平移个单位,得到对应点C的坐标为即.
故选:D.
9.C
【分析】本题主要考查了估算无理数大小.首先根据题意可知该微观粒子的能量,结合,易得,即可获得答案.
【详解】解:当,时,
,
∵,
∴,
∴该微观粒子的能量的值在6和7之间.
故选:C.
10.D
【分析】本题考查了平行线的性质,关键是熟练掌握平行线的性质,注意整体思想的运用.过点作,令与交于点,先设角,利用平行线的性质表示出待求角,再利用整体思想即可求解.
【详解】解:设
则,,,
过点作,令与交于点,
∵,
∴,
∴,,,
∴
;
;
∴
故选:D.
二.填空题
11.4
【分析】本题考查平方根的性质,根据正数的平方根互为相反数求出x值是解题的关键.
由正数的平方根互为相反数,可得,即可求得x的值,再根据平方根的概念求解即可.
【详解】解:∵一个正数的两个平方根分别是与,
∴
解得:,
∴
∴这个正数是.
故答案为:4.
12.
【分析】内错角在截线的两侧,在被截线的内侧.
【详解】如图所示,与∠C是内错角的是∠2,∠3;
故答案是:∠2,∠3.
13.
【分析】本题主要考查平行于轴点的坐标特点,熟练掌握平行于轴点的坐标特点是解题的关键.根据平行于轴点的坐标特点得到值相等即可得到答案.
【详解】解: 平行于轴,
,
故,
故答案为:.
14.64°.
【分析】由角平分线的性质和平行线的性质,即可求出答案.
【详解】解:∵AD∥BC,∠B=32°,
∴∠ADB=∠B=32°.
∵DB平分∠ADE,
∴∠ADE=2∠ADB=64°,
∵AD∥BC,
∴∠DEC=∠ADE=64°.
故答案为:64°.
15.2
【分析】本题考查二元一次方程组的解、解二元一次方程组,将代入,将两个方程相加可得答案.
【详解】解:将代入,得:,
得:,
解得,
故答案为:2.
16.96
【分析】本题主要考查平行线和角平分线.熟练掌握平行线的判定和性质,角平分线的定义,角的和差倍分计算,添加辅助线,是解题关键.
过点M作,过点E作,可得,结合角平分线的计算得,结合图形利用各角之间的数量关系得出,由已知条件求解即可得出结果.
【详解】解:如图所示,过点M作,过点E作,
∵,
∴,
∴,,,,
∵ 平分,平分,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故答案为:96.
三.解答题
17.(1)解;
;
(2)解:
.
18.(1)解:,
得:,
解得:,
把代入①得:,
解得:,
∴原方程的解为:;
(2)解:,
原方程组可变为:,
由①得,
把③代入②得:,
解得:,
把代入③得:,
∴原方程组的解为:.
19.(1)解:如图所示:
点的坐标为;
(2) 边上一点经过上述平移后的对应点为,
点;
(3)的面积为:
.
20.(1)解:∵平分,,
∴,
∵,
∴,
∴,
(2)解:∵,
∴可设
∵平分,
∴,
∴,
∵,
∴,
∴
∴x=22.5 °=,
即的度数为.
21.(1)解: ,即,
的整数部分c为3,
一个数的两个平方根分别是和,的立方根是,是的整数部分,
,,,
解得:,,;
(2)解:由(1)可知:,,,
,
的平方根为:.
22.证明:如图2,延长交于点 P.
∵(已知)
∴ (两直线平行,内错角相等)
又∵( 已知 ),
∴(等量代换).
∴ (同位角相等,两直线平行).
∴(两直线平行,同旁内角互补).
又∵(已知)
∴(两直线平行,同旁内角互补)
∴( 同角的补角相等).
23.解:任务1,设A款奶茶的销售单价是x元,B款奶茶的销售单价是y元,由题意得:
,
解得:;
答:A款奶茶的销售单价是10元,B款奶茶的销售单价是12元;
任务2,设购买A种款式的奶茶m杯,购买B种款式的奶茶n杯,由题意得:
,
整理得:,
∵m、n均为正整数,
∴或或,
∴有3种购买方案;
任务3:设小华购买的奶茶中,A款不加料的奶茶买了a杯,A款加料的奶茶和B款不加料的奶茶共买了b杯,
则B款加料的奶茶买了杯,即杯,
由题意得:,
整理得:,
∵a、b、均为正整数,
∴,
∴;
答:B款加料的奶茶买了11杯.
24.(1)解:过点P作,则,
∵,,
∴,,
∴,
∵,
∴;
(2)解:①当在和之间时,如图2,
∵,,
∴,
∴射线运动的时间秒,
∴射线旋转的角度,
又∵,
∴;
当在和之间时,如图3所示,
∵,,
∴,
∴射线ME运动的时间秒,
∴射线旋转的角度,
又∵,
∴;
∴的度数为或;
②当,即时,若,如图,
则,即,
解得:,不合题意,舍去;
当时,若,如图,
则,即,
解得:;
当时,若,如图,
则,即,
解得:;
当时,不存在互相平行的情况;
综上,当时,t的值是或.
一.选择题(共10小题,满分30分,每小题3分)
1.下列命题中,是真命题的是( )
A.相等的角是对顶角
B.同位角互补,两直线平行
C.同位角相等
D.在同一平面内,垂直于同一条直线的两条直线互相平行
2.下列实数:,其中最小的是( )
A. B.0 C. D.
3.若点的坐标满足条件,则点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.如果方程组的解为,那么被“”“”遮住的两个数分别是( )
A., B., C., D.,
5.如图是某运动员在一次山地自行车越野赛中经过的路线,已知第一次的拐角,第三次的拐角,若第三次拐弯后的道路恰好与第一次拐弯前的道路平行,则第二次的拐角的度数为( )
A. B. C. D.
6.在平面直角坐标系中,点与点关于x轴对称,则的值是( )
A. B.2 C. D.
7.若关于,的二元一次方程组的解也是二元一次方程的解,则的值为( )
A. B. C. D.
8.如图,在平面直角坐标系中,将线段平移后得到线段,点和点的对应点分别是点和点.若点,,,则点的坐标为( )
A. B. C. D.
9.在量子物理的研究中,科学家需要精确计算微观粒子的能量、已知某微观粒子的能量可以用公式表示.当,时,该微观粒子的能量的值在( )
A.4和5之间 B.5和6之间 C.6和7之间 D.8和9之间
10.如图,,则与的数量关系是( )
A. B.
C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.一个正数的两个平方根分别是与,则这个正数是 .
12.如图,与是内错角的是 .
13.已知点和点,且平行于轴,则点坐标为 .
14.如图,已知,,平分,则 .
15.已知是方程组的解,则的值为 .
16.如图,平分,平分,的反向延长线交于点,若,则 .
三.解答题(共8小题,满分72分)
17.(6分)计算:
(1) (2)
18.(6分)解下列方程组:
(1) (2)
19.(8分)如图,在平面直角坐标系中,三个顶点的坐标分别为,,.将向右平移个单位长度,再向下平移个单位长度,得到,其中点,,分别为点,,的对应点.
(1)请在所给坐标系中画出,并直接写出点的坐标;
(2)若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标;(直接写出结果即可)
(3)求的面积.
20.(8分)如图,已知直线、相交于点O,,点O为垂足,平分.
(1)若,求的度数;
(2)若,求的度数.
21.(10分)已知一个数的两个平方根分别是和,的立方根为,c是的整数部分.
(1)求a,b,c的值.
(2)求的平方根.
22.(10分)读懂下面的推理过程,并填空 (理由或数学式).
中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图1是一个“互”字,如图2是由图1抽象出的几何图形,其中,点E,M,F在同一直线上,点G,H,N在同一条直线上,且,.求证:
证明:如图2,延长交于点 P.
∵(已知)
∴ ( )
又∵( 已知 ),
∴ (等量代换).
∴ ( ).
∴ (两直线平行,同旁内角互补).
又∵ (已知)
∴( )
∴( 同角的补角相等).
23.(12分)【背景】为了激励学习好的学生,班主任去奶茶店购买A、B两种款式的奶茶作为奖品.如图所示.
【素材1】若买3杯A款奶茶,2杯B款奶茶,共需54元;若买2杯A款奶茶,3杯B款奶茶,共需56元.
【素材2】为了满足市场的需求,奶茶店推出每杯2元的加料服务,顾客在选完款式后可以自主选择加料一份或者不加料.
【任务1】求A款奶茶和B款奶茶的销售单价各是多少元?
【任务2】在不加料的情况下,购买A、B两种款式的奶茶(两种都要),刚好花220元,请问有几种购买方案?
【任务3】根据【素材2】小华恰好用了260元购买A、B两款奶茶,其中A款不加料的杯数是总杯数的.求B款加料的奶茶买了多少杯?
24.(12分)如图,已知是直线,间的一点,于点,交于点, .
(1) .
(2)如图2,射线从出发,以每秒的速度绕点按逆时针方向旋转,当垂直时,立刻按原速返回至后停止运动;射线从出发,以每秒的速度绕点按逆时针方向旋转至后停止运动,若射线,射线同时开始运动,设运动时间为秒.
①当时,请求出的度数;
②当时,请求出的值.
参考答案
一.选择题
1.D
【分析】本题考查了命题,根据对顶角的定义、平行线的判定和性质逐项判断即可求解,掌握以上知识点是解题的关键.
【详解】解:、相等的角不一定是对顶角,该选项命题是假命题,不合题意;
、同位角相等,两直线平行,该选项命题是假命题,不合题意;
、两直线平行,同位角相等,该选项命题是假命题,不合题意;
、在同一平面内,垂直于同一条直线的两条直线互相平行,该选项命题是真命题,符合题意;
故选:.
2.A
【分析】本题考查了实数的大小比较,根据实数的大小比较方法即可得出答案,掌握实数的大小比较方法是解题的关键.
【详解】解:∵,
∴最小的是,
故选:A.
3.D
【分析】本题考查了平方的非负性、绝对值的非负性、平面直角坐标系中点的坐标.首先根据平方的非负性和绝对值的非负性得到,,从而可得点的坐标为,根据坐标判断点所在原象限.
【详解】解:
又,,
,,
解得:,,
点的坐标为,
点在第四象限.
故选:D.
4.A
【分析】本题考查二元一次方程组的解,把代入先求出,再代入求出.解题的关键是理解方程组解的定义.
【详解】解:∵方程组的解为,
∴分别为方程和的解,
∴,
∴,
∴,
∴,
∴被“”“”遮住的两个数分别是,.
故选:A.
5.A
【分析】本题考查了平行线的判定与性质,过点作直线,根据平行线的性质得到,再得到,得出,即可求解,掌握相关知识是解题的关键.
【详解】解:如解图,过点作直线,
∴,
∵,且,
∴,
∴,
∵,
∴,
∴,
故选:A.
6.D
【分析】本题考查关于x轴对称的点的坐标,立方根,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数,可得m、n的值,再求的立方根即可.
【详解】解:点与点关于x轴对称,
,,
,,
,
故选D.
7.B
【分析】本题考查了解二元一次方程组和解一元一次方程,先解方程组,用含k的代数式表示x、y,再把x、y的值代入二元一次方程中,求出k.
【详解】解:,
,得,
∴,
,得,
∴,
∵二元一次方程组的解也是二元一次方程的解,
∴,
即,
∴.
故选:B.
8.D
【分析】本题考查了平移与坐标,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.根据点、的坐标确定出平移方式,再根据平移方式结合图形解答即可.
【详解】解:点的对应点,
平移规律为向右平移个单位,再向上平移个单位,
向右平移个单位,再向上平移个单位,得到对应点C的坐标为即.
故选:D.
9.C
【分析】本题主要考查了估算无理数大小.首先根据题意可知该微观粒子的能量,结合,易得,即可获得答案.
【详解】解:当,时,
,
∵,
∴,
∴该微观粒子的能量的值在6和7之间.
故选:C.
10.D
【分析】本题考查了平行线的性质,关键是熟练掌握平行线的性质,注意整体思想的运用.过点作,令与交于点,先设角,利用平行线的性质表示出待求角,再利用整体思想即可求解.
【详解】解:设
则,,,
过点作,令与交于点,
∵,
∴,
∴,,,
∴
;
;
∴
故选:D.
二.填空题
11.4
【分析】本题考查平方根的性质,根据正数的平方根互为相反数求出x值是解题的关键.
由正数的平方根互为相反数,可得,即可求得x的值,再根据平方根的概念求解即可.
【详解】解:∵一个正数的两个平方根分别是与,
∴
解得:,
∴
∴这个正数是.
故答案为:4.
12.
【分析】内错角在截线的两侧,在被截线的内侧.
【详解】如图所示,与∠C是内错角的是∠2,∠3;
故答案是:∠2,∠3.
13.
【分析】本题主要考查平行于轴点的坐标特点,熟练掌握平行于轴点的坐标特点是解题的关键.根据平行于轴点的坐标特点得到值相等即可得到答案.
【详解】解: 平行于轴,
,
故,
故答案为:.
14.64°.
【分析】由角平分线的性质和平行线的性质,即可求出答案.
【详解】解:∵AD∥BC,∠B=32°,
∴∠ADB=∠B=32°.
∵DB平分∠ADE,
∴∠ADE=2∠ADB=64°,
∵AD∥BC,
∴∠DEC=∠ADE=64°.
故答案为:64°.
15.2
【分析】本题考查二元一次方程组的解、解二元一次方程组,将代入,将两个方程相加可得答案.
【详解】解:将代入,得:,
得:,
解得,
故答案为:2.
16.96
【分析】本题主要考查平行线和角平分线.熟练掌握平行线的判定和性质,角平分线的定义,角的和差倍分计算,添加辅助线,是解题关键.
过点M作,过点E作,可得,结合角平分线的计算得,结合图形利用各角之间的数量关系得出,由已知条件求解即可得出结果.
【详解】解:如图所示,过点M作,过点E作,
∵,
∴,
∴,,,,
∵ 平分,平分,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故答案为:96.
三.解答题
17.(1)解;
;
(2)解:
.
18.(1)解:,
得:,
解得:,
把代入①得:,
解得:,
∴原方程的解为:;
(2)解:,
原方程组可变为:,
由①得,
把③代入②得:,
解得:,
把代入③得:,
∴原方程组的解为:.
19.(1)解:如图所示:
点的坐标为;
(2) 边上一点经过上述平移后的对应点为,
点;
(3)的面积为:
.
20.(1)解:∵平分,,
∴,
∵,
∴,
∴,
(2)解:∵,
∴可设
∵平分,
∴,
∴,
∵,
∴,
∴
∴x=22.5 °=,
即的度数为.
21.(1)解: ,即,
的整数部分c为3,
一个数的两个平方根分别是和,的立方根是,是的整数部分,
,,,
解得:,,;
(2)解:由(1)可知:,,,
,
的平方根为:.
22.证明:如图2,延长交于点 P.
∵(已知)
∴ (两直线平行,内错角相等)
又∵( 已知 ),
∴(等量代换).
∴ (同位角相等,两直线平行).
∴(两直线平行,同旁内角互补).
又∵(已知)
∴(两直线平行,同旁内角互补)
∴( 同角的补角相等).
23.解:任务1,设A款奶茶的销售单价是x元,B款奶茶的销售单价是y元,由题意得:
,
解得:;
答:A款奶茶的销售单价是10元,B款奶茶的销售单价是12元;
任务2,设购买A种款式的奶茶m杯,购买B种款式的奶茶n杯,由题意得:
,
整理得:,
∵m、n均为正整数,
∴或或,
∴有3种购买方案;
任务3:设小华购买的奶茶中,A款不加料的奶茶买了a杯,A款加料的奶茶和B款不加料的奶茶共买了b杯,
则B款加料的奶茶买了杯,即杯,
由题意得:,
整理得:,
∵a、b、均为正整数,
∴,
∴;
答:B款加料的奶茶买了11杯.
24.(1)解:过点P作,则,
∵,,
∴,,
∴,
∵,
∴;
(2)解:①当在和之间时,如图2,
∵,,
∴,
∴射线运动的时间秒,
∴射线旋转的角度,
又∵,
∴;
当在和之间时,如图3所示,
∵,,
∴,
∴射线ME运动的时间秒,
∴射线旋转的角度,
又∵,
∴;
∴的度数为或;
②当,即时,若,如图,
则,即,
解得:,不合题意,舍去;
当时,若,如图,
则,即,
解得:;
当时,若,如图,
则,即,
解得:;
当时,不存在互相平行的情况;
综上,当时,t的值是或.
同课章节目录
