人教版八年级数学下册试题第18章平行四边形综合测试卷(含详解)
文档属性
| 名称 | 人教版八年级数学下册试题第18章平行四边形综合测试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 08:45:17 | ||
图片预览

文档简介
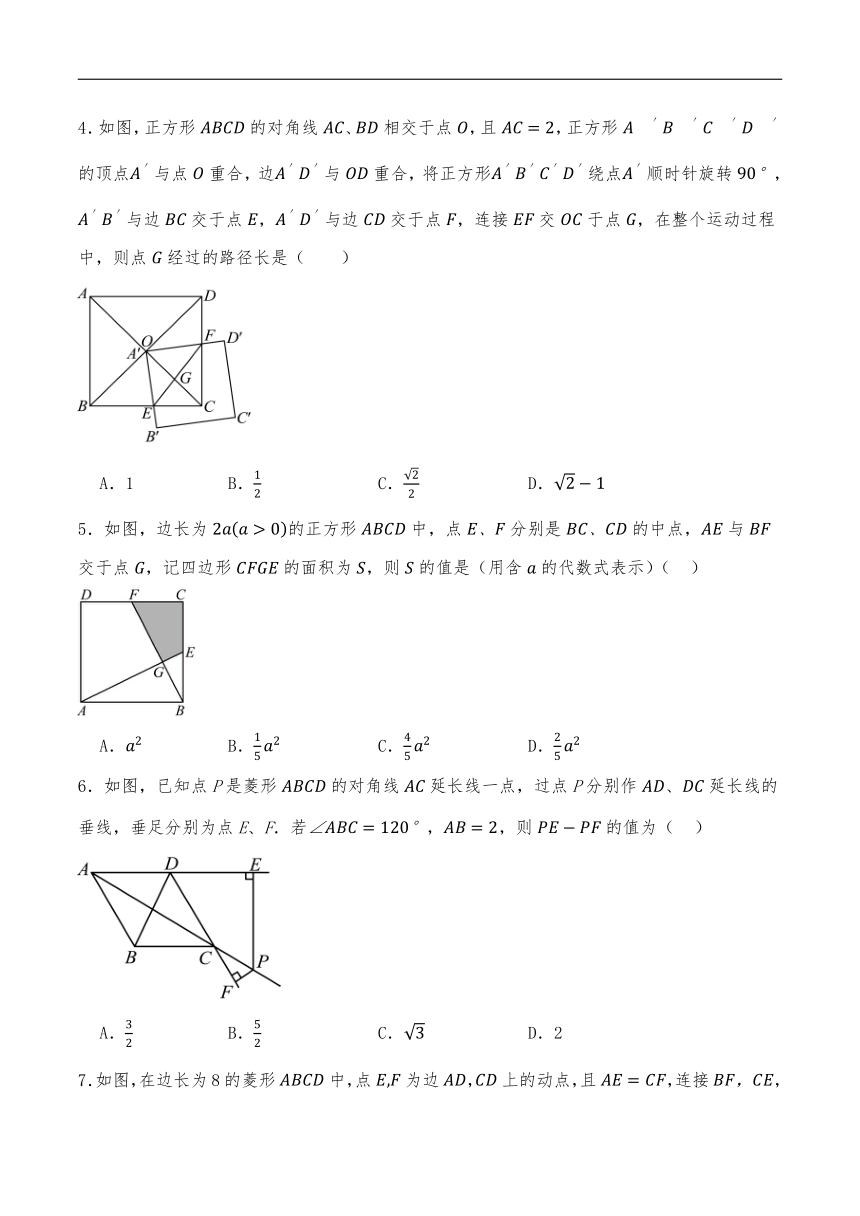
第18章《 平行四边形》综合测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.如图,中,对角线相交于点,,,,则的长为( )
A. B. C. D.
2.如图,为等腰,,,,在一条直线上,且四边形为矩形,若,,,分别为,的中点,连接,则的长为( )
A. B. C. D.
3.在菱形中,,,点在上,,若点是菱形四条边上异于点的一点,,则以下长度中,不可能是的长度的是( )
A. B.4 C. D.
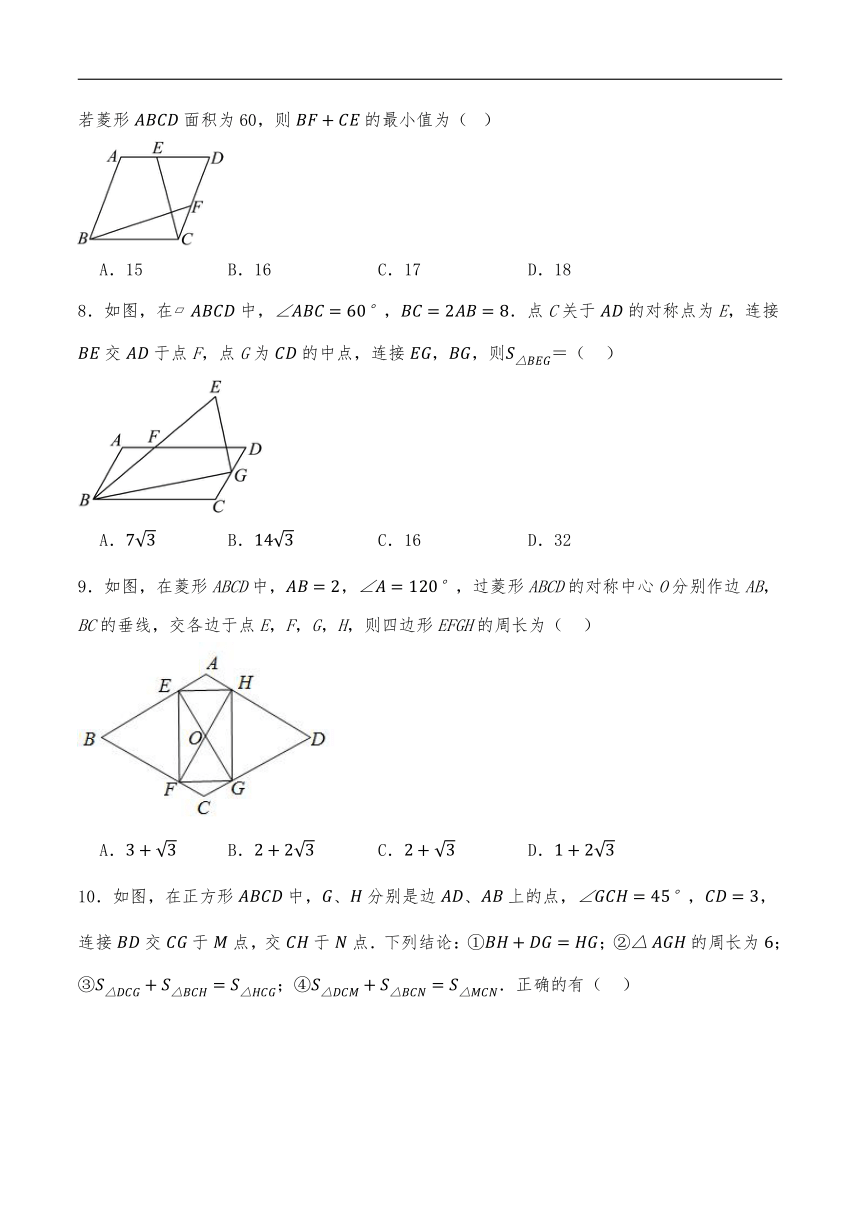
4.如图,正方形的对角线、相交于点,且,正方形的顶点与点重合,边与重合,将正方形绕点顺时针旋转,与边交于点,与边交于点,连接交于点,在整个运动过程中,则点经过的路径长是( )
A.1 B. C. D.
5.如图,边长为的正方形中,点分别是的中点,与交于点,记四边形的面积为,则的值是(用含的代数式表示)( )
A. B. C. D.
6.如图,已知点P是菱形的对角线延长线一点,过点P分别作、延长线的垂线,垂足分别为点E、F.若,,则的值为( )
A. B. C. D.2
7.如图,在边长为8的菱形中,点为边,上的动点,且,连接,若菱形面积为60,则的最小值为( )
A.15 B.16 C.17 D.18
8.如图,在中,,.点C关于的对称点为E,连接交于点F,点G为的中点,连接,,则=( )
A. B. C.16 D.32
9.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
10.如图,在正方形中,、分别是边、上的点,,,连接交于点,交于点.下列结论:①;②的周长为;③;④.正确的有( )
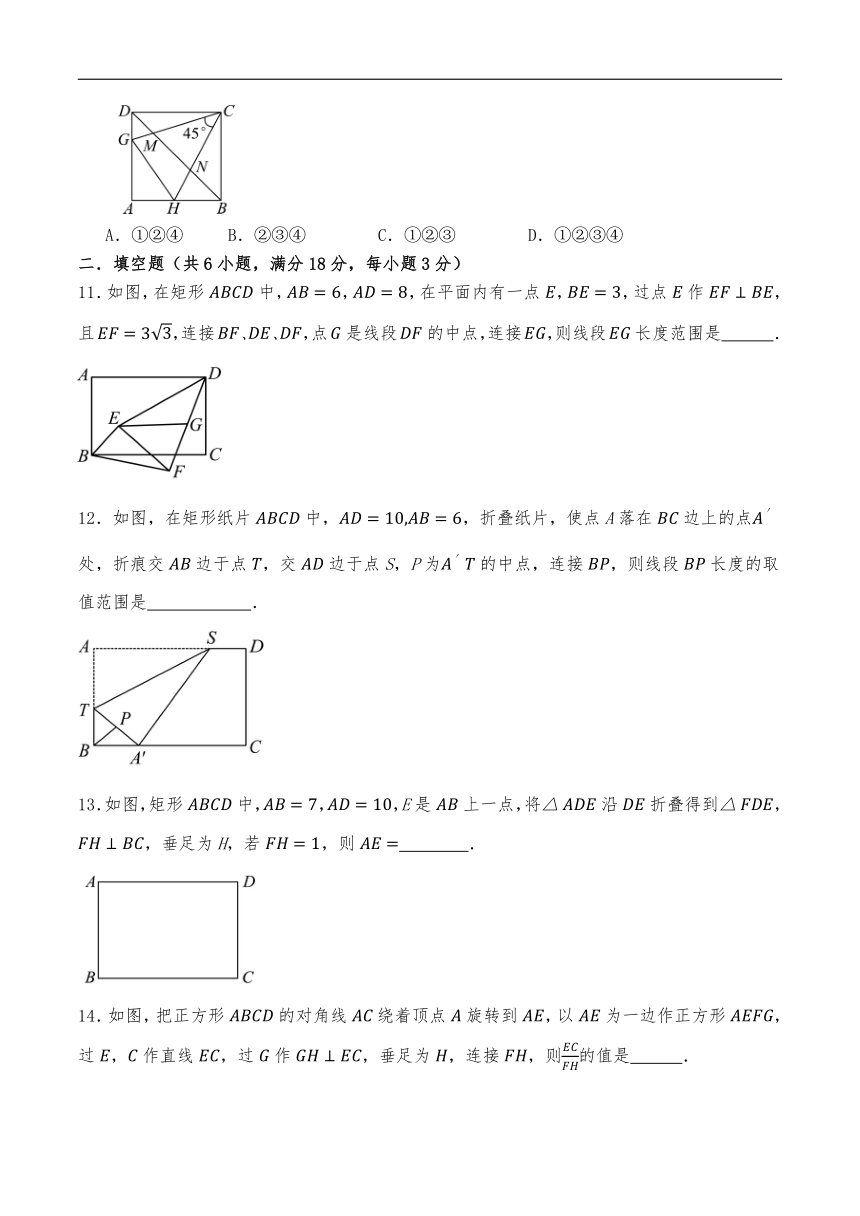
A.①②④ B.②③④ C.①②③ D.①②③④
二.填空题(共6小题,满分18分,每小题3分)
11.如图,在矩形中,,,在平面内有一点,,过点作,且,连接、、,点是线段的中点,连接,则线段长度范围是 .
12.如图,在矩形纸片中,,折叠纸片,使点A落在边上的点处,折痕交边于点,交边于点S,P为的中点,连接,则线段长度的取值范围是 .
13.如图,矩形中,,,E是上一点,将沿折叠得到,,垂足为H,若,则 .
14.如图,把正方形的对角线绕着顶点旋转到,以为一边作正方形,过,作直线,过作,垂足为,连接,则的值是 .
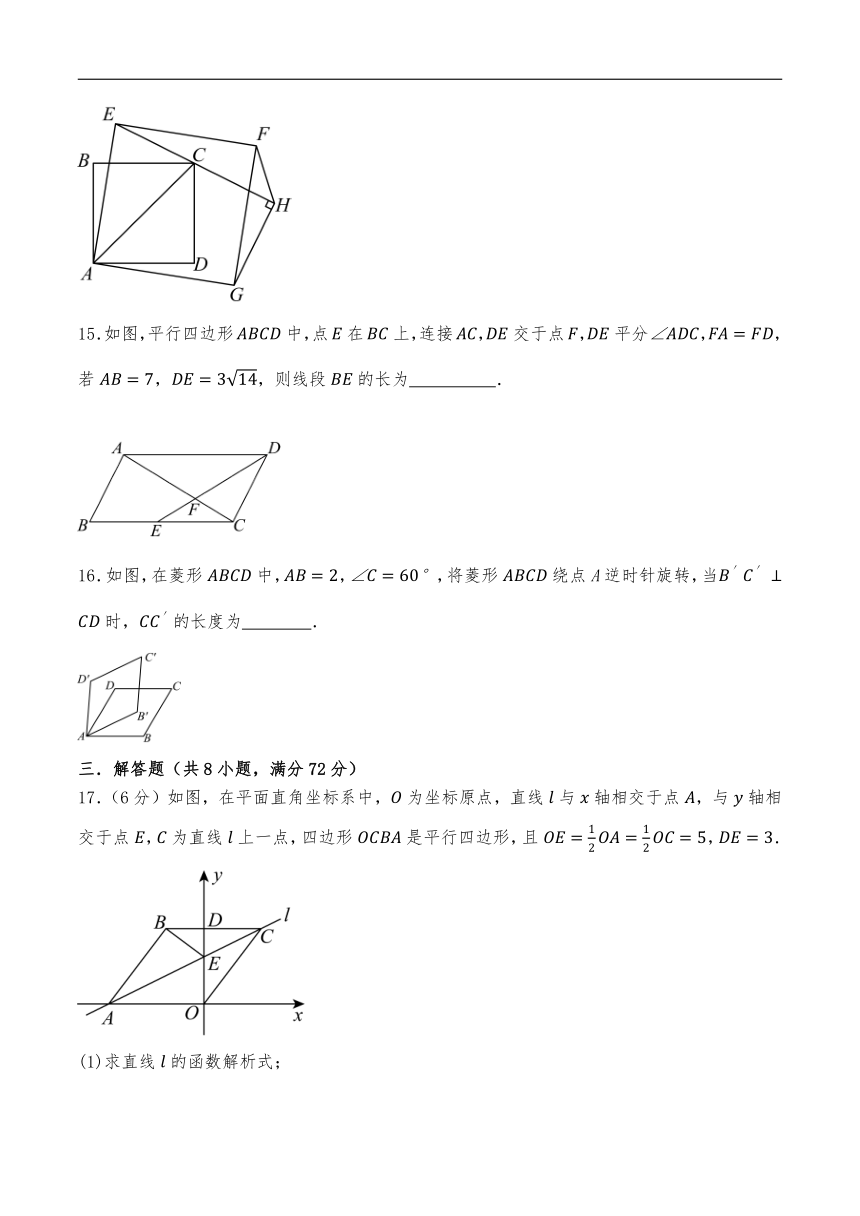
15.如图,平行四边形中,点在上,连接,交于点,平分,,若,,则线段的长为 .
16.如图,在菱形中,,,将菱形绕点A逆时针旋转,当时,的长度为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,在平面直角坐标系中,为坐标原点,直线与轴相交于点,与轴相交于点,为直线上一点,四边形是平行四边形,且,.
(1)求直线的函数解析式;
(2)点从点出发,沿路线以每秒3个单位的速度匀速运动,当点到达点时停止运动,设点运动时间为秒,在运动过程中是否存在点使的面积为,若存在,求出点的坐标,若不存在,请说明理由.
18.(6分)(1)如图1, 在中,与相交于点, 过点的直线交于点, 交于点, 则与的数量关系是 ;
(2)在中,,请仅用无刻度的直尺,按要求完成以下的作图(保留作图痕迹).
①如图2, 点在边上, 且, 作的平分线;
②如图3, 点,分别在边,上,且,连接,过点作的垂线.
19.(8分)如图,在平面直角坐标系中,点,点,点,以、为边作,点为中点,连接、.
(1)分别求出线段和线段所在直线解析式;
(2)点为线段上的一个动点,作点关于点的中心对称点,设点横坐标为,用含的代数式表示点的坐标(不用写出的取值范围);
(3)在(2)的条件下,
①当点移动到的边上时,求点坐标;
②为中点,为中点,连接、.请利用备用图探究,直接写出在点的运动过程中,周长的最小值和此时点的坐标.
20.(8分)已知:如图,在四边形和中,,.点P是边上一点,且,M是延长线上一点,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图1,若,求证:;
(3)如图2,连接,若,求的长.
21.(10分)在四边形中,对角线,相交于点,过点的两条直线,分别交边,,,于点,,,.
【问题发现】
(1)如图1,若四边形是正方形,且,则_____;
【问题探究】
(2)如图2,若四边形是矩形,且满足,设,,,求的长(用含,,的代数式表示);
【问题解决】
(3)如图3,张大伯有一块平行四边形菜地,且米,米,点处是一口水井,且米,是原先就有的一条沟渠,且经过平行四边形菜地的对角线的交点,张大伯准备再修建一条经过点的沟渠,将该菜地分成四个面积相等的部分,并分别种上四种不同的蔬菜,试确定点的位置.
22.(10分)平行四边形在平面直角坐标系中的位置如图①.
(1)写出点C的坐标;
(2)在图①中,连接,得到图②,求与的交点M的坐标;
(3)将图②中的线段向两方延长得到图③,若点 D、E为直线上不与B、C重合的动点,是否存在这样的点D、E,使得四边形为矩形?若存在,请在图中画出矩形,并求出矩形的面积和点 D、E 的坐标,若不存在,请说明理由.
23.(12分)综合与实践
问题情境:如图1,四边形是菱形,过点作于点,过点作于点.
解决问题:
(1)四边形是( )
A. 平行四边形 B. 矩形 C. 正方形
(2)若,,则四边形的面积为 ;
深入探究:
(3)将图1中的绕点逆时针旋转,得到,点的对应点分别为点.
①如图2,当线段经过点时,所在直线分别与线段交于点.猜想线段与的数量关系,并说明理由;
②当直线与直线垂直时,直线直线交于点.若,,则线段的长度为 .
24.(12分)如图1,在平面直角坐标系中,点,点,以为边在右侧作正方形.
(1)当点B在x轴正半轴上运动时,求点C的坐标(用m表示);
(2)当时,如图2,P为上一点,连接,过点P作,过A作,与交于点M,求证:;
(3)在(2)的条件下,如图3,连交于点N,求的值.
参考答案
一.选择题
1.B
【分析】本题考查了平行四边形的性质,等腰直角三角形的性质,勾股定理,过点作于,过点作的延长线于,由可得,由勾股定理得,由平行四边形性质得,,进而得到,,,即可得到,,即得,由勾股定理即可求出的长,正确作出辅助线是解题的关键.
【详解】解:如图,过点作于,过点作的延长线于,则,
∵,
∴,
∴,
∵,,
∴,
∵四边形是平行四边形,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴,,
∴,
∵,
∴为等腰直角三角形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
故选:.
2.A
【分析】延长至,使,连接,根据连接三角形任意两边中点的连线叫中位线,三角形的中位线平行于第三边且等于第三边的一半可得,,推得,根据两边和它们的夹角对应相等的两个三角形全等,全等三角形的对应边相等可得,推得,设,根据矩形的对边相等可得,求得,根据直角三角形两锐角互余得出,根据直角三角形中角所对的边是斜边的一半可得,根据直角三角形两直角边的平方和等于斜边的平方求出的值,即可列出方程,解方程求出的值,即可求解.
【详解】解:如图,延长至,使,连接,
∵为的中点,
∴,
又∵,
∴,,
∵为的中点,
∴,
∴,
在和中,
,
∴,
∴,
∴;
设,
∵四边形为矩形,
∴,
∴,
在中,,
∴,
∴,
由勾股定理得:,
则,
解得:,
∴,
∴.
故选:A.
3.C
【分析】分点位于边上、位于边上、位于边上三种情况讨论,利用含30度角的直角三角形的性质以及勾股定理求解即可.
【详解】解:当点位于边上时,如图所示:
菱形中,,,
,,
;
当点位于边上时,如图所示:
菱形中,,,
是等边三角形,
过点作于点,
,
由勾股定理得,
,
点与点重合,
;
当点位于边上时,
,,,
,
,
由勾股定理得.
综上,的长为或4或.
故选:C.
4.A
【分析】取中点,利用正方形的性质证明,得到,当时,易证此时四边形是正方形,此时,即点G与点H重合,有最小值,利用正方形的性质求出;由点是与的交点,是定线段,得到点G在线段上运动,在整个运动过程中,当边与重合,点G,点E与点C重合,当时,点G与点H重合,当边与重合,点G,点F与点C重合,即点G在整个运动过程中,由点C运动到点H,再由点H运动到点C,即点经过的路径长是,即可得出结果.
【详解】解:如图,取中点,
在正方形中,,
又∵,
∴,
∴,
,
当时,
则,
,,
四边形是正方形,
,即点G与点H重合,
,
;
点是与的交点,是定线段,,
点G在线段上运动,
在整个运动过程中,
当边与重合,点G,点E与点C重合,有最大值,
当时,点G与点H重合,有最小值,
当边与重合,点G,点F与点C重合,有最大值,
点G在整个运动过程中,由点C运动到点H,再由点H运动到点C,
点经过的路径长是,
点经过的路径长是,
故选:A.
5.C
【分析】本题主要考查了全等三角形的判定与性质,勾股定理,正方形的性质等知识点,熟练掌握全等三角形的判定与性质,灵活运用勾股定理和三角形的面积公式进行计算是解决问题的关键,连接,依题意得,证明和全等得,,进而可证明,根据三角形的面积公式求出,则,再由勾股定理得,继而得,,然后根据即可得出答案.
【详解】解:连接,如图所示:
四边形是正方形,边长为,
,,
点分别是的中点,
,
在中,由勾股定理得:,
在和中,
,
,
,,
,
,
,
,
在中,由勾股定理得,
,,
,
故选:C.
6.C
【分析】本题主要考查菱形的性质、勾股定理、含角的直角三角形的性质等知识点,求出、将转换为是解题的关键.
如图:连接交于O,由菱形的性质与勾股定理得到,则,再由,,则即可解答.
【详解】解:如图:连接交于O,
∵四边形是菱形,,,
∴ AD∥BC,AB∥CD ,,,
,
在中,,
,
,
在中,,
,
在中,,
,
.
故选C.
7.C
【分析】本题主要考查了菱形与三角形综合.熟练掌握菱形性质,全等三角形的判定和性质,轴对称性质,勾股定理,是解题的关键.
作点C关于的对称点G,连接交于点H,连接,则,可得,根据,得,得,得,根据菱形性质和,可得,得,得,得取得最小值为17 .
【详解】作点C关于的对称点G,连接交于点H,连接,
则,,,
∵,
∴,
∵,
∴,
∴,
∴,
∵菱形中,,且,
∴,
∴,
∴,
∴当点E在线段上时,取得最小值17.
故选:C.
8.B
【分析】如图,取中点,连接,连接交于,作交的延长线于.构建计算即可
【详解】解:如图,取中点,连接,连接交于,作交的延长线于.
,,,
,
是等边三角形,
,
,
,
,,
,,
,
,,
,,
.
故选B.
9.A
【分析】依次求出OE=OF=OG=OH,利用勾股定理得出EF和OE的长,即可求出该四边形的周长.
【详解】∵HF⊥BC,EG⊥AB,
∴∠BEO=∠BFO=90°,
∵∠A=120°,
∴∠B=60°,
∴∠EOF=120°,∠EOH=60°,
由菱形的对边平行,得HF⊥AD,EG⊥CD,
因为O点是菱形ABCD的对称中心,
∴O点到各边的距离相等,即OE=OF=OG=OH,
∴∠OEF=∠OFE=30°,∠OEH=∠OHE=60°,
∴∠HEF=∠EFG=∠FGH=∠EHG=90°,
所以四边形EFGH是矩形;
设OE=OF=OG=OH=x,
∴EG=HF=2x,,
如图,连接AC,则AC经过点O,
可得三角形ABC是等边三角形,
∴∠BAC=60°,AC=AB=2,
∴OA=1,∠AOE=30°,
∴AE=,
∴x=OE=
∴四边形EFGH的周长为EF+FG+GH+HE=,
故选A.
10.C
【分析】本题主要考查了正方形的性质,全等三角形的性质和判定,旋转的性质等,构造全等三角形是解题的关键.由四边形是正方形得, ,,再将绕点逆时针旋转得到,在上取一点,使,根据旋转的性质及证明 ,然后根据全等三角形的性质判断①②③;再证明 ,可得,,,然后说明 ,最后根据全等三角形的面积相等判断④即可.
【详解】∵四边形是正方形,
∴, ,.
将绕点逆时针旋转得到,则共线,在上取一点,使.
根据旋转的性质可知,,.
∵,,
∴,
∴,
即.
∵,,
∴ ,
∴,
∴的周长 .
故①②③正确;
∵,,,
∴ ,
∴.
∵,,,
∴ ,
∴,
∴.
所以④不正确.
正确的有①②③.
故选:C.
二.填空题
11.
【分析】本题考查了矩形的性质、三角形的中位线定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,利用三角形的中位线定理构造辅助线是解题关键.取的中点,连接,先根据矩形的性质和勾股定理求出,再根据勾股定理可得,根据直角三角形斜边上的中线等于斜边的一半可得,然后根据三角形的三边关系即可得.
【详解】解:如图,取的中点,连接,
∵四边形是矩形,
∴,
∵,,
∴,
∵,,,
∴,
∵,点为的中点,
∴,
又∵点是线段的中点,点为的中点,
∴,
由三角形的三边关系得:(当且仅当点共线时,等号成立),
∴,即,
故答案为:.
12.
【分析】本题是四边形综合题,考查了矩形的性质,折叠的性质,直角三角形的性质,勾股定理等知识,灵活运用这些性质进行推理是本题的关键.
根据题意,由折叠的性质以及直角三角形的性质,知,分以下两种情况当时,最长, 最长;当时,最短,最短,分别讨论,设,则,结合勾股定理即可得出线段长度的取值范围,线段长度的取值范围即可求解.
【详解】由折叠的性质可知:,
在中,P为的中点
,
由题可得:当时,最长,最长值为6,如下图:
当时,最短,如下图:
设,则,
在中,
,,
,
,
在中,由勾股定理得:,
解得:,
,
.
13.或
【分析】分两种情况讨论:当点在上方时,过点作,交于点,交于点,由矩形的性质可得,,,由平行公理的推论可得,由两直线平行同旁内角互补可得,,可证得四边形是矩形,于是可得,可证得四边形是矩形,于是可得,由邻补角互补可得,,进而可证得四边形是矩形,于是可得,,由折叠的性质可得,,在中,根据勾股定理可得,则,设,则,,在中,根据勾股定理可得,即,解方程即可求出的长;当点在下方时,过点作,交的延长线于点,交的延长线于点,推导过程与完全相同,同理可得的长;综上,可得答案.
【详解】解:分两种情况讨论:
当点在上方时,
如图,过点作,交于点,交于点,
,
,
四边形是矩形,
,,,
,
,
,
,
,
四边形是矩形,
,
,
四边形是矩形,
,
,
,
,
四边形是矩形,
,,
由折叠的性质可得:
,,
在中,根据勾股定理可得:
,
,
设,则,,
在中,根据勾股定理可得:
,
即:,
解得:,
;
当点在下方时,
如图,过点作,交的延长线于点,交的延长线于点,
推导过程与完全相同,
同理可得:;
综上,或,
故答案为:或.
14.
【分析】过作于点,过作于点,根据等腰三角形的性质可得,又四边形是正方形,可得,,通过同角的余角相等得,即可证明,根据性质得,过作交于点,设与交于点,再证明,则,由勾股定理得出,最后代入即可求解.
【详解】解:如图,过作于点,过作于点,
∴,
∵,
∴,
∵四边形是正方形,
∴,,
∴,,
∴,
∴,
∴,
过作交于点,
∴,
∴,
∴,
设与交于点,
∵,
∴,
∵,,
∴,
∴,
∴为等腰直角三角形,
∴,
∴,
∴为等腰直角三角形,
∴由勾股定理得:,
∵,
∴,
∴,
故答案为:.
15.4
【分析】本题考查了平行四边形的性质,全等三角形的判定与性质,等腰三角形的性质,平行线的性质,角平分线的性质,长方形的性质,勾股定理,解二元一次方程组等知识点.正确地作出辅助线是解题的关键.
首先利用证明,从而得;然后根据平行四边形的性质,平行线的性质,角平分线的性质,证明;作于点,于点,则有四边形是长方形;最后根据勾股定理列出关于、的二元一次方程组求解即可.
【详解】如图,连结,
四边形是平行四边形,
,,,.
,
,
,
,
,
又 ,
.
.
平分,
,
,
.
作于点,于点,
则有四边形是长方形,
.
设,,则,.
在中,
①;
在中,
②;
联立①②,解得.
则.
故线段的长为4.
16.或
【分析】本题考查了菱形的性质,旋转的性质,勾股定理.分两种情况讨论,作于,延长交于,交于,连接,利用直角三角形性质和勾股定理求得,和的长,在中,求得,利用勾股定理即可求解.
【详解】解:如图,作于,延长交于,交于,连接,
∵在菱形中,,,
∴,,,,
由旋转的性质得,,,
∴,
又∵,
∴,即,
∴,
∴三点共线,
在中,,,
∴,,
∵,
∴四边形是矩形,
∴,
在中,,,
∴,
∴,
∴,
在中,,
∴;
如图,
同理,,,
,
∴;
综上,的长度为或.
故答案为:或.
三.解答题
17.(1)∵,
∴,
∴,
设直线的函数解析式为,
则,解得,
∴直线的函数解析式为;
(2)∵四边形是平行四边形,,,
∴,轴,
∴四边形是菱形,,
∵,
∴,
∴,
当点M在BC上, ,
若存在,则,
即,解得:,
∴,
∴;
当点M在上, ,
∵四边形是菱形,
∴,
∵,
∴,
∴,
∴,
即,解得,
∴,
此时,点M为的中点,
∵,
∴;
综上,存在点M,使的面积为,点的坐标为或.
18.解:(1),理由如下:
四边形是平行四边形
,
在和中
故答案为:
(2)连接,
又
平分
故如图所示,即为所求:
(3)连接、、、,、交于点, 连接延长交与点,连接,
四边形是平行四边形
,
,
四边形是平行四边形
又
平行四边形是菱形
在和中
四边形为平行四边形
故如图所示,即为所求,
19.(1)解:∵,,
∴,
∵四边形为平行四边形,,
∴,
∵点为中点,
∴,
设所在直线的解析式为,
把,代入得:
,解得:,
∴所在直线的解析式为;
设所在直线解析式为,
把点,代入的:
,解得:,
∴所在直线解析式为.
(2)解:∵所在直线的解析式为,点横坐标为,
∴点,
设点,
∵点和点关于点的中心对称点,
∴,
整理得:,
∴;
(3)解:①当点在上时,
∵点在上,
∴,解得,
∴;
当点在上时,
∵,且在上,
∴,解得:,
∴;
综上:或;
②∵,,
∴,
∵为中点,为中点,
∴,
过点作轴于点,
∵,,
∴,
∴,则,
过点作于点,过点作于点,
∵点是点关于点的中心对称点,
∴,
又∵,
∴,
∴,
延长,过点作于点,
∵点是中点,
∴,
∵,
∴,
∴,则,
∵,,
∴,
∵,,
∴设,
在中,根据勾股定理可得:,即,
解得:,
∴,
过点作,
∵,,,
∴,
则点在直线上运动,
作点关于直线的对称点,
根据轴对称的性质以及平行线间的距离处处相等可得,
当点,,在同一条直线上时,,此时周长取最小值,
在中,根据勾股定理可得:,
∴周长最小值为;
∵,,,为中点,为中点,
∴,,
∵,,
∴是的中位线,则点是中点,
∴,
过点作于点,
∵,,
∴,
∴
∵,
∴,即点为中点,
∴,
∵,
∴,解得:,
∴
20.(1)证明:∵,
∴,
∵,
∴,
∴,
∴四边形是平行四边形;
(2)证明:∵,
∴,即,
又∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(3)解:如图,延长到点N,使,连接,
∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∴,
∵,,
∴,
∴,
∴,即,
由(1)可得,四边形是平行四边形,
又∵,
∴四边形是正方形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
又∵,
∴,
∴,
由勾股定理得,,即,
解得,,(舍去),
∴的长为.
21.解:(1)如图1,四边形是正方形,
,,
在与中,
,
,
,
故答案为.
(2)解:如图2,过作于N,于M,
,
,
,
,
,.
,
(3)解:如图3,过作,,则,,
,
,
,
,
,,
,解得米,
米,
当时,能将该菜地分成四个面积相等的部分.
22.(1)解:四边形是平行四边形,
,
、,
;
(2)解:如图②,设所在的直线的解析式为,
直线经过点、,
,
解得:
所在直线的解析式为,
由于直线过原点,
设直线的表达式为,
将点代入,得,
解得:,
直线的表达式为,
联立方程
解得:,
即的坐标是;
(3)解:存在这样的、,使得四边形是矩形.
分别过点、作于点,于点,过、分别作轴的垂线和的垂线,垂足分别为、,
四边形是平行四边形,
,
,
四边形是矩形,且与平行四边形面积相等,
平行四边形的面积为,
矩形的面积为12,即,
,
,
四边形是矩形,
,
,
,
,
,
点的坐标为,
四边形是矩形,四边形是平行四边形,
,,,,
,,
,
,
,
,
,
,
点的坐标为.
23.解:(1),
,
四边形为菱形,
∴,
∴,
,
∴,
四边形为矩形,
故选:B.
(2)∵,,,
∴,,
∵四边形是菱形,
∴,
∴,
∵四边形为矩形,
∴面积为:,
故答案为:;
(3)①.理由如下:
∵四边形为菱形,
,
旋转得到,
,
,
,
,
,
,
.
②解:如图所示,当点N在线段上时,过点A作于P,
∵四边形是菱形,
∴,,
∵,
∴,
,
∴,
由旋转知:,,,
∴,
∵,
∴,
∴,
∴四边形为矩形,
∵,
∴四边形为正方形,
∴,
∵,
∴;
当点N在线段延长线上时,在上,过点A作于K,连接,如图所示:
由旋转知:,,,,
∵,
∴,
∴,,
∵四边形是菱形,
∴,,
∵,
∴,
,
∴,,
∵,
∴ 四边形为矩形,
∵,
∴四边形为正方形,
∴,,
∴,
综上,的长度为1或7,
故答案为:1或7.
24.(1)如图1中,作轴于E.
,
,,
,
,
,
,,
.
(2)如图,在上取点Q,使,连接,
正方形为对角线,
,,,
,
,
①,,
,
,
,
,
,
,
,②
由①②知:,
,
.
(3)如图,过M作交于F.
正方形,
,
∴
,,
四边形是平行四边形,
,,,
,
,
,
,
.
一.选择题(共10小题,满分30分,每小题3分)
1.如图,中,对角线相交于点,,,,则的长为( )
A. B. C. D.
2.如图,为等腰,,,,在一条直线上,且四边形为矩形,若,,,分别为,的中点,连接,则的长为( )
A. B. C. D.
3.在菱形中,,,点在上,,若点是菱形四条边上异于点的一点,,则以下长度中,不可能是的长度的是( )
A. B.4 C. D.
4.如图,正方形的对角线、相交于点,且,正方形的顶点与点重合,边与重合,将正方形绕点顺时针旋转,与边交于点,与边交于点,连接交于点,在整个运动过程中,则点经过的路径长是( )
A.1 B. C. D.
5.如图,边长为的正方形中,点分别是的中点,与交于点,记四边形的面积为,则的值是(用含的代数式表示)( )
A. B. C. D.
6.如图,已知点P是菱形的对角线延长线一点,过点P分别作、延长线的垂线,垂足分别为点E、F.若,,则的值为( )
A. B. C. D.2
7.如图,在边长为8的菱形中,点为边,上的动点,且,连接,若菱形面积为60,则的最小值为( )
A.15 B.16 C.17 D.18
8.如图,在中,,.点C关于的对称点为E,连接交于点F,点G为的中点,连接,,则=( )
A. B. C.16 D.32
9.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
10.如图,在正方形中,、分别是边、上的点,,,连接交于点,交于点.下列结论:①;②的周长为;③;④.正确的有( )
A.①②④ B.②③④ C.①②③ D.①②③④
二.填空题(共6小题,满分18分,每小题3分)
11.如图,在矩形中,,,在平面内有一点,,过点作,且,连接、、,点是线段的中点,连接,则线段长度范围是 .
12.如图,在矩形纸片中,,折叠纸片,使点A落在边上的点处,折痕交边于点,交边于点S,P为的中点,连接,则线段长度的取值范围是 .
13.如图,矩形中,,,E是上一点,将沿折叠得到,,垂足为H,若,则 .
14.如图,把正方形的对角线绕着顶点旋转到,以为一边作正方形,过,作直线,过作,垂足为,连接,则的值是 .
15.如图,平行四边形中,点在上,连接,交于点,平分,,若,,则线段的长为 .
16.如图,在菱形中,,,将菱形绕点A逆时针旋转,当时,的长度为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,在平面直角坐标系中,为坐标原点,直线与轴相交于点,与轴相交于点,为直线上一点,四边形是平行四边形,且,.
(1)求直线的函数解析式;
(2)点从点出发,沿路线以每秒3个单位的速度匀速运动,当点到达点时停止运动,设点运动时间为秒,在运动过程中是否存在点使的面积为,若存在,求出点的坐标,若不存在,请说明理由.
18.(6分)(1)如图1, 在中,与相交于点, 过点的直线交于点, 交于点, 则与的数量关系是 ;
(2)在中,,请仅用无刻度的直尺,按要求完成以下的作图(保留作图痕迹).
①如图2, 点在边上, 且, 作的平分线;
②如图3, 点,分别在边,上,且,连接,过点作的垂线.
19.(8分)如图,在平面直角坐标系中,点,点,点,以、为边作,点为中点,连接、.
(1)分别求出线段和线段所在直线解析式;
(2)点为线段上的一个动点,作点关于点的中心对称点,设点横坐标为,用含的代数式表示点的坐标(不用写出的取值范围);
(3)在(2)的条件下,
①当点移动到的边上时,求点坐标;
②为中点,为中点,连接、.请利用备用图探究,直接写出在点的运动过程中,周长的最小值和此时点的坐标.
20.(8分)已知:如图,在四边形和中,,.点P是边上一点,且,M是延长线上一点,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图1,若,求证:;
(3)如图2,连接,若,求的长.
21.(10分)在四边形中,对角线,相交于点,过点的两条直线,分别交边,,,于点,,,.
【问题发现】
(1)如图1,若四边形是正方形,且,则_____;
【问题探究】
(2)如图2,若四边形是矩形,且满足,设,,,求的长(用含,,的代数式表示);
【问题解决】
(3)如图3,张大伯有一块平行四边形菜地,且米,米,点处是一口水井,且米,是原先就有的一条沟渠,且经过平行四边形菜地的对角线的交点,张大伯准备再修建一条经过点的沟渠,将该菜地分成四个面积相等的部分,并分别种上四种不同的蔬菜,试确定点的位置.
22.(10分)平行四边形在平面直角坐标系中的位置如图①.
(1)写出点C的坐标;
(2)在图①中,连接,得到图②,求与的交点M的坐标;
(3)将图②中的线段向两方延长得到图③,若点 D、E为直线上不与B、C重合的动点,是否存在这样的点D、E,使得四边形为矩形?若存在,请在图中画出矩形,并求出矩形的面积和点 D、E 的坐标,若不存在,请说明理由.
23.(12分)综合与实践
问题情境:如图1,四边形是菱形,过点作于点,过点作于点.
解决问题:
(1)四边形是( )
A. 平行四边形 B. 矩形 C. 正方形
(2)若,,则四边形的面积为 ;
深入探究:
(3)将图1中的绕点逆时针旋转,得到,点的对应点分别为点.
①如图2,当线段经过点时,所在直线分别与线段交于点.猜想线段与的数量关系,并说明理由;
②当直线与直线垂直时,直线直线交于点.若,,则线段的长度为 .
24.(12分)如图1,在平面直角坐标系中,点,点,以为边在右侧作正方形.
(1)当点B在x轴正半轴上运动时,求点C的坐标(用m表示);
(2)当时,如图2,P为上一点,连接,过点P作,过A作,与交于点M,求证:;
(3)在(2)的条件下,如图3,连交于点N,求的值.
参考答案
一.选择题
1.B
【分析】本题考查了平行四边形的性质,等腰直角三角形的性质,勾股定理,过点作于,过点作的延长线于,由可得,由勾股定理得,由平行四边形性质得,,进而得到,,,即可得到,,即得,由勾股定理即可求出的长,正确作出辅助线是解题的关键.
【详解】解:如图,过点作于,过点作的延长线于,则,
∵,
∴,
∴,
∵,,
∴,
∵四边形是平行四边形,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴,,
∴,
∵,
∴为等腰直角三角形,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
故选:.
2.A
【分析】延长至,使,连接,根据连接三角形任意两边中点的连线叫中位线,三角形的中位线平行于第三边且等于第三边的一半可得,,推得,根据两边和它们的夹角对应相等的两个三角形全等,全等三角形的对应边相等可得,推得,设,根据矩形的对边相等可得,求得,根据直角三角形两锐角互余得出,根据直角三角形中角所对的边是斜边的一半可得,根据直角三角形两直角边的平方和等于斜边的平方求出的值,即可列出方程,解方程求出的值,即可求解.
【详解】解:如图,延长至,使,连接,
∵为的中点,
∴,
又∵,
∴,,
∵为的中点,
∴,
∴,
在和中,
,
∴,
∴,
∴;
设,
∵四边形为矩形,
∴,
∴,
在中,,
∴,
∴,
由勾股定理得:,
则,
解得:,
∴,
∴.
故选:A.
3.C
【分析】分点位于边上、位于边上、位于边上三种情况讨论,利用含30度角的直角三角形的性质以及勾股定理求解即可.
【详解】解:当点位于边上时,如图所示:
菱形中,,,
,,
;
当点位于边上时,如图所示:
菱形中,,,
是等边三角形,
过点作于点,
,
由勾股定理得,
,
点与点重合,
;
当点位于边上时,
,,,
,
,
由勾股定理得.
综上,的长为或4或.
故选:C.
4.A
【分析】取中点,利用正方形的性质证明,得到,当时,易证此时四边形是正方形,此时,即点G与点H重合,有最小值,利用正方形的性质求出;由点是与的交点,是定线段,得到点G在线段上运动,在整个运动过程中,当边与重合,点G,点E与点C重合,当时,点G与点H重合,当边与重合,点G,点F与点C重合,即点G在整个运动过程中,由点C运动到点H,再由点H运动到点C,即点经过的路径长是,即可得出结果.
【详解】解:如图,取中点,
在正方形中,,
又∵,
∴,
∴,
,
当时,
则,
,,
四边形是正方形,
,即点G与点H重合,
,
;
点是与的交点,是定线段,,
点G在线段上运动,
在整个运动过程中,
当边与重合,点G,点E与点C重合,有最大值,
当时,点G与点H重合,有最小值,
当边与重合,点G,点F与点C重合,有最大值,
点G在整个运动过程中,由点C运动到点H,再由点H运动到点C,
点经过的路径长是,
点经过的路径长是,
故选:A.
5.C
【分析】本题主要考查了全等三角形的判定与性质,勾股定理,正方形的性质等知识点,熟练掌握全等三角形的判定与性质,灵活运用勾股定理和三角形的面积公式进行计算是解决问题的关键,连接,依题意得,证明和全等得,,进而可证明,根据三角形的面积公式求出,则,再由勾股定理得,继而得,,然后根据即可得出答案.
【详解】解:连接,如图所示:
四边形是正方形,边长为,
,,
点分别是的中点,
,
在中,由勾股定理得:,
在和中,
,
,
,,
,
,
,
,
在中,由勾股定理得,
,,
,
故选:C.
6.C
【分析】本题主要考查菱形的性质、勾股定理、含角的直角三角形的性质等知识点,求出、将转换为是解题的关键.
如图:连接交于O,由菱形的性质与勾股定理得到,则,再由,,则即可解答.
【详解】解:如图:连接交于O,
∵四边形是菱形,,,
∴ AD∥BC,AB∥CD ,,,
,
在中,,
,
,
在中,,
,
在中,,
,
.
故选C.
7.C
【分析】本题主要考查了菱形与三角形综合.熟练掌握菱形性质,全等三角形的判定和性质,轴对称性质,勾股定理,是解题的关键.
作点C关于的对称点G,连接交于点H,连接,则,可得,根据,得,得,得,根据菱形性质和,可得,得,得,得取得最小值为17 .
【详解】作点C关于的对称点G,连接交于点H,连接,
则,,,
∵,
∴,
∵,
∴,
∴,
∴,
∵菱形中,,且,
∴,
∴,
∴,
∴当点E在线段上时,取得最小值17.
故选:C.
8.B
【分析】如图,取中点,连接,连接交于,作交的延长线于.构建计算即可
【详解】解:如图,取中点,连接,连接交于,作交的延长线于.
,,,
,
是等边三角形,
,
,
,
,,
,,
,
,,
,,
.
故选B.
9.A
【分析】依次求出OE=OF=OG=OH,利用勾股定理得出EF和OE的长,即可求出该四边形的周长.
【详解】∵HF⊥BC,EG⊥AB,
∴∠BEO=∠BFO=90°,
∵∠A=120°,
∴∠B=60°,
∴∠EOF=120°,∠EOH=60°,
由菱形的对边平行,得HF⊥AD,EG⊥CD,
因为O点是菱形ABCD的对称中心,
∴O点到各边的距离相等,即OE=OF=OG=OH,
∴∠OEF=∠OFE=30°,∠OEH=∠OHE=60°,
∴∠HEF=∠EFG=∠FGH=∠EHG=90°,
所以四边形EFGH是矩形;
设OE=OF=OG=OH=x,
∴EG=HF=2x,,
如图,连接AC,则AC经过点O,
可得三角形ABC是等边三角形,
∴∠BAC=60°,AC=AB=2,
∴OA=1,∠AOE=30°,
∴AE=,
∴x=OE=
∴四边形EFGH的周长为EF+FG+GH+HE=,
故选A.
10.C
【分析】本题主要考查了正方形的性质,全等三角形的性质和判定,旋转的性质等,构造全等三角形是解题的关键.由四边形是正方形得, ,,再将绕点逆时针旋转得到,在上取一点,使,根据旋转的性质及证明 ,然后根据全等三角形的性质判断①②③;再证明 ,可得,,,然后说明 ,最后根据全等三角形的面积相等判断④即可.
【详解】∵四边形是正方形,
∴, ,.
将绕点逆时针旋转得到,则共线,在上取一点,使.
根据旋转的性质可知,,.
∵,,
∴,
∴,
即.
∵,,
∴ ,
∴,
∴的周长 .
故①②③正确;
∵,,,
∴ ,
∴.
∵,,,
∴ ,
∴,
∴.
所以④不正确.
正确的有①②③.
故选:C.
二.填空题
11.
【分析】本题考查了矩形的性质、三角形的中位线定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,利用三角形的中位线定理构造辅助线是解题关键.取的中点,连接,先根据矩形的性质和勾股定理求出,再根据勾股定理可得,根据直角三角形斜边上的中线等于斜边的一半可得,然后根据三角形的三边关系即可得.
【详解】解:如图,取的中点,连接,
∵四边形是矩形,
∴,
∵,,
∴,
∵,,,
∴,
∵,点为的中点,
∴,
又∵点是线段的中点,点为的中点,
∴,
由三角形的三边关系得:(当且仅当点共线时,等号成立),
∴,即,
故答案为:.
12.
【分析】本题是四边形综合题,考查了矩形的性质,折叠的性质,直角三角形的性质,勾股定理等知识,灵活运用这些性质进行推理是本题的关键.
根据题意,由折叠的性质以及直角三角形的性质,知,分以下两种情况当时,最长, 最长;当时,最短,最短,分别讨论,设,则,结合勾股定理即可得出线段长度的取值范围,线段长度的取值范围即可求解.
【详解】由折叠的性质可知:,
在中,P为的中点
,
由题可得:当时,最长,最长值为6,如下图:
当时,最短,如下图:
设,则,
在中,
,,
,
,
在中,由勾股定理得:,
解得:,
,
.
13.或
【分析】分两种情况讨论:当点在上方时,过点作,交于点,交于点,由矩形的性质可得,,,由平行公理的推论可得,由两直线平行同旁内角互补可得,,可证得四边形是矩形,于是可得,可证得四边形是矩形,于是可得,由邻补角互补可得,,进而可证得四边形是矩形,于是可得,,由折叠的性质可得,,在中,根据勾股定理可得,则,设,则,,在中,根据勾股定理可得,即,解方程即可求出的长;当点在下方时,过点作,交的延长线于点,交的延长线于点,推导过程与完全相同,同理可得的长;综上,可得答案.
【详解】解:分两种情况讨论:
当点在上方时,
如图,过点作,交于点,交于点,
,
,
四边形是矩形,
,,,
,
,
,
,
,
四边形是矩形,
,
,
四边形是矩形,
,
,
,
,
四边形是矩形,
,,
由折叠的性质可得:
,,
在中,根据勾股定理可得:
,
,
设,则,,
在中,根据勾股定理可得:
,
即:,
解得:,
;
当点在下方时,
如图,过点作,交的延长线于点,交的延长线于点,
推导过程与完全相同,
同理可得:;
综上,或,
故答案为:或.
14.
【分析】过作于点,过作于点,根据等腰三角形的性质可得,又四边形是正方形,可得,,通过同角的余角相等得,即可证明,根据性质得,过作交于点,设与交于点,再证明,则,由勾股定理得出,最后代入即可求解.
【详解】解:如图,过作于点,过作于点,
∴,
∵,
∴,
∵四边形是正方形,
∴,,
∴,,
∴,
∴,
∴,
过作交于点,
∴,
∴,
∴,
设与交于点,
∵,
∴,
∵,,
∴,
∴,
∴为等腰直角三角形,
∴,
∴,
∴为等腰直角三角形,
∴由勾股定理得:,
∵,
∴,
∴,
故答案为:.
15.4
【分析】本题考查了平行四边形的性质,全等三角形的判定与性质,等腰三角形的性质,平行线的性质,角平分线的性质,长方形的性质,勾股定理,解二元一次方程组等知识点.正确地作出辅助线是解题的关键.
首先利用证明,从而得;然后根据平行四边形的性质,平行线的性质,角平分线的性质,证明;作于点,于点,则有四边形是长方形;最后根据勾股定理列出关于、的二元一次方程组求解即可.
【详解】如图,连结,
四边形是平行四边形,
,,,.
,
,
,
,
,
又 ,
.
.
平分,
,
,
.
作于点,于点,
则有四边形是长方形,
.
设,,则,.
在中,
①;
在中,
②;
联立①②,解得.
则.
故线段的长为4.
16.或
【分析】本题考查了菱形的性质,旋转的性质,勾股定理.分两种情况讨论,作于,延长交于,交于,连接,利用直角三角形性质和勾股定理求得,和的长,在中,求得,利用勾股定理即可求解.
【详解】解:如图,作于,延长交于,交于,连接,
∵在菱形中,,,
∴,,,,
由旋转的性质得,,,
∴,
又∵,
∴,即,
∴,
∴三点共线,
在中,,,
∴,,
∵,
∴四边形是矩形,
∴,
在中,,,
∴,
∴,
∴,
在中,,
∴;
如图,
同理,,,
,
∴;
综上,的长度为或.
故答案为:或.
三.解答题
17.(1)∵,
∴,
∴,
设直线的函数解析式为,
则,解得,
∴直线的函数解析式为;
(2)∵四边形是平行四边形,,,
∴,轴,
∴四边形是菱形,,
∵,
∴,
∴,
当点M在BC上, ,
若存在,则,
即,解得:,
∴,
∴;
当点M在上, ,
∵四边形是菱形,
∴,
∵,
∴,
∴,
∴,
即,解得,
∴,
此时,点M为的中点,
∵,
∴;
综上,存在点M,使的面积为,点的坐标为或.
18.解:(1),理由如下:
四边形是平行四边形
,
在和中
故答案为:
(2)连接,
又
平分
故如图所示,即为所求:
(3)连接、、、,、交于点, 连接延长交与点,连接,
四边形是平行四边形
,
,
四边形是平行四边形
又
平行四边形是菱形
在和中
四边形为平行四边形
故如图所示,即为所求,
19.(1)解:∵,,
∴,
∵四边形为平行四边形,,
∴,
∵点为中点,
∴,
设所在直线的解析式为,
把,代入得:
,解得:,
∴所在直线的解析式为;
设所在直线解析式为,
把点,代入的:
,解得:,
∴所在直线解析式为.
(2)解:∵所在直线的解析式为,点横坐标为,
∴点,
设点,
∵点和点关于点的中心对称点,
∴,
整理得:,
∴;
(3)解:①当点在上时,
∵点在上,
∴,解得,
∴;
当点在上时,
∵,且在上,
∴,解得:,
∴;
综上:或;
②∵,,
∴,
∵为中点,为中点,
∴,
过点作轴于点,
∵,,
∴,
∴,则,
过点作于点,过点作于点,
∵点是点关于点的中心对称点,
∴,
又∵,
∴,
∴,
延长,过点作于点,
∵点是中点,
∴,
∵,
∴,
∴,则,
∵,,
∴,
∵,,
∴设,
在中,根据勾股定理可得:,即,
解得:,
∴,
过点作,
∵,,,
∴,
则点在直线上运动,
作点关于直线的对称点,
根据轴对称的性质以及平行线间的距离处处相等可得,
当点,,在同一条直线上时,,此时周长取最小值,
在中,根据勾股定理可得:,
∴周长最小值为;
∵,,,为中点,为中点,
∴,,
∵,,
∴是的中位线,则点是中点,
∴,
过点作于点,
∵,,
∴,
∴
∵,
∴,即点为中点,
∴,
∵,
∴,解得:,
∴
20.(1)证明:∵,
∴,
∵,
∴,
∴,
∴四边形是平行四边形;
(2)证明:∵,
∴,即,
又∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∵,
∴;
(3)解:如图,延长到点N,使,连接,
∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∴,
∵,,
∴,
∴,
∴,即,
由(1)可得,四边形是平行四边形,
又∵,
∴四边形是正方形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
又∵,
∴,
∴,
由勾股定理得,,即,
解得,,(舍去),
∴的长为.
21.解:(1)如图1,四边形是正方形,
,,
在与中,
,
,
,
故答案为.
(2)解:如图2,过作于N,于M,
,
,
,
,
,.
,
(3)解:如图3,过作,,则,,
,
,
,
,
,,
,解得米,
米,
当时,能将该菜地分成四个面积相等的部分.
22.(1)解:四边形是平行四边形,
,
、,
;
(2)解:如图②,设所在的直线的解析式为,
直线经过点、,
,
解得:
所在直线的解析式为,
由于直线过原点,
设直线的表达式为,
将点代入,得,
解得:,
直线的表达式为,
联立方程
解得:,
即的坐标是;
(3)解:存在这样的、,使得四边形是矩形.
分别过点、作于点,于点,过、分别作轴的垂线和的垂线,垂足分别为、,
四边形是平行四边形,
,
,
四边形是矩形,且与平行四边形面积相等,
平行四边形的面积为,
矩形的面积为12,即,
,
,
四边形是矩形,
,
,
,
,
,
点的坐标为,
四边形是矩形,四边形是平行四边形,
,,,,
,,
,
,
,
,
,
,
点的坐标为.
23.解:(1),
,
四边形为菱形,
∴,
∴,
,
∴,
四边形为矩形,
故选:B.
(2)∵,,,
∴,,
∵四边形是菱形,
∴,
∴,
∵四边形为矩形,
∴面积为:,
故答案为:;
(3)①.理由如下:
∵四边形为菱形,
,
旋转得到,
,
,
,
,
,
,
.
②解:如图所示,当点N在线段上时,过点A作于P,
∵四边形是菱形,
∴,,
∵,
∴,
,
∴,
由旋转知:,,,
∴,
∵,
∴,
∴,
∴四边形为矩形,
∵,
∴四边形为正方形,
∴,
∵,
∴;
当点N在线段延长线上时,在上,过点A作于K,连接,如图所示:
由旋转知:,,,,
∵,
∴,
∴,,
∵四边形是菱形,
∴,,
∵,
∴,
,
∴,,
∵,
∴ 四边形为矩形,
∵,
∴四边形为正方形,
∴,,
∴,
综上,的长度为1或7,
故答案为:1或7.
24.(1)如图1中,作轴于E.
,
,,
,
,
,
,,
.
(2)如图,在上取点Q,使,连接,
正方形为对角线,
,,,
,
,
①,,
,
,
,
,
,
,
,②
由①②知:,
,
.
(3)如图,过M作交于F.
正方形,
,
∴
,,
四边形是平行四边形,
,,,
,
,
,
,
.
