2009年海南省海口市高中数学优质课评选活动参赛课例----导数的几何意义
文档属性
| 名称 | 2009年海南省海口市高中数学优质课评选活动参赛课例----导数的几何意义 |

|
|
| 格式 | rar | ||
| 文件大小 | 65.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-05 12:38:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题:导数的几何意义
海口市琼山中学 郭小兰
教材:人教A版选修2-2
教学目标:
1、知识与技能 :
理解导数的几何意义;
2、过程与方法:
经历导数几何意义的学习过程,体会用导数的几何意义分析图象上点的变化情况的方法。
3、情感态度与价值观:
体会导数与曲线的联系,初步认识数学的科学价值,发展理性思维能力。
教学重点:
理解导数的几何意义;
教学难点:
理解函数的导数就是在某点处的切线的斜率。
教具准备:多媒体课件,三角板。
教学过程:
一、引入新课
师:在前面的学习中,我们知道函数y=f(x)在x=x0处的导数就是函数y=f(x)在x=x0处的瞬时变化率,这是导数的物理意义,那么导数的几何意义是什么呢?我们本节课就来学习导数的几何意义。
板书课题:导数的几何意义
二.讲授新课
教师引导学生观察右图,回答下面问题:
师: 初中平面几何中我们是如何定义圆的切线和割线的?
生:根据直线和圆的交点个数,有一个交点时,直线是圆的切线;
有两个交点时,直线是圆的割线。
师补充说明
1. 圆的切线在点P附近位于圆的一侧(为一般曲线的切线做准备);
2. 当点Pn趋近于点P时,圆的割线PPn趋近于圆的切线PT。当点Pn与点P重合时,割线变成了切线。
师:对于一般曲线的切线和割线,它们又具有怎样的位置关系呢?
探究一:观察一般曲线y=f(x)割线的变化趋势,教师引导学生给出一般曲线的切线定义。
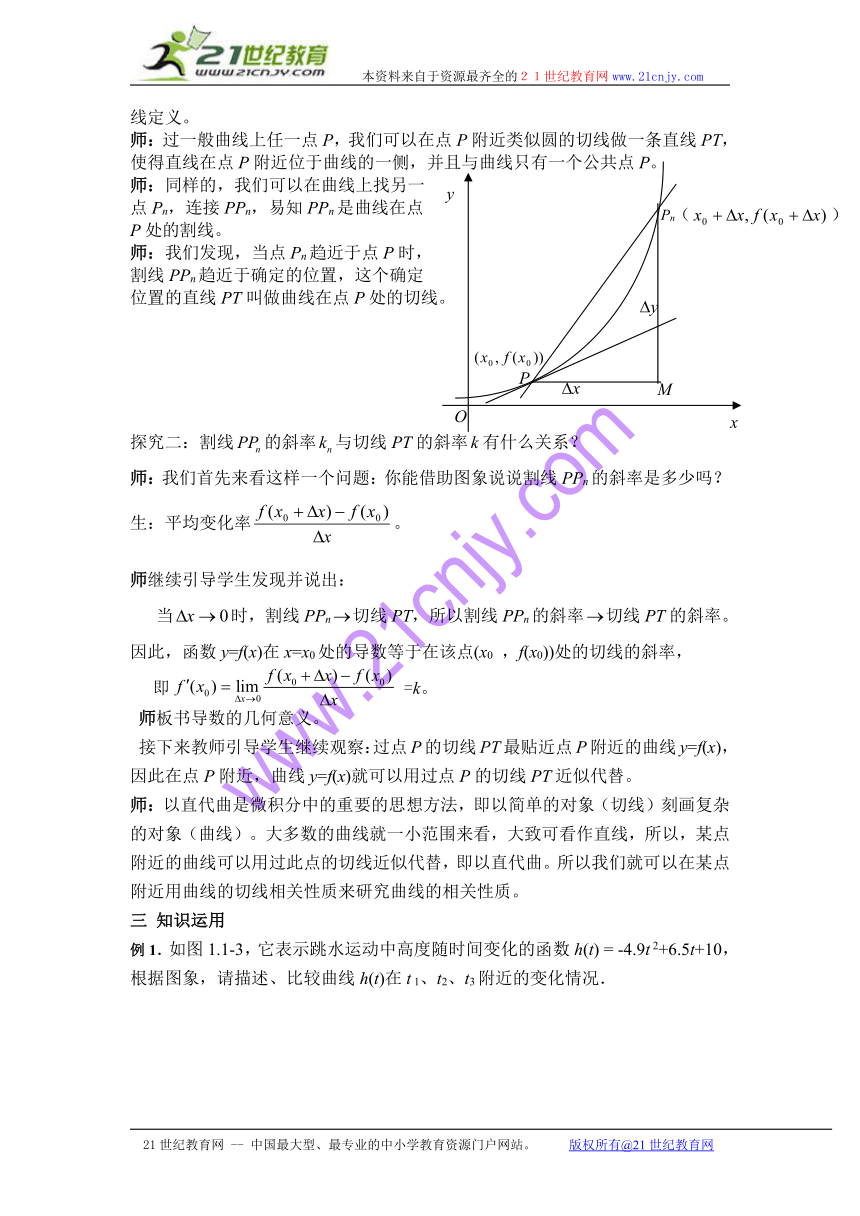
师:过一般曲线上任一点P,我们可以在点P附近类似圆的切线做一条直线PT,使得直线在点P附近位于曲线的一侧,并且与曲线只有一个公共点P。
师:同样的,我们可以在曲线上找另一
点Pn,连接PPn,易知PPn是曲线在点
P处的割线。
师:我们发现,当点Pn趋近于点P时,
割线PPn趋近于确定的位置,这个确定
位置的直线PT叫做曲线在点P处的切线。
探究二:割线的斜率与切线PT的斜率有什么关系?
师:我们首先来看这样一个问题:你能借助图象说说割线PPn的斜率是多少吗?
生:平均变化率。
师继续引导学生发现并说出:
当时,割线PPn切线PT,所以割线PPn的斜率切线PT的斜率。因此,函数y=f(x)在x=x0处的导数等于在该点(x0 ,f(x0))处的切线的斜率,
即 =k。
师板书导数的几何意义。
接下来教师引导学生继续观察:过点P的切线PT最贴近点P附近的曲线y=f(x),因此在点P附近,曲线y=f(x)就可以用过点P的切线PT近似代替。
师:以直代曲是微积分中的重要的思想方法,即以简单的对象(切线)刻画复杂的对象(曲线)。大多数的曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即以直代曲。所以我们就可以在某点附近用曲线的切线相关性质来研究曲线的相关性质。
三 知识运用
例1.如图1.1-3,它表示跳水运动中高度随时间变化的函数h(t) = -4.9t 2+6.5t+10,根据图象,请描述、比较曲线h(t)在t 1、t2、t3附近的变化情况.
解析:借助于几何画板,引导学生运用“以直代曲”的思想由切线斜率的正负得到切线的升降情况,从而得到在切点附近曲线的升降情况。
师引导学生分析题目条件,教师讲解t 1处,然后由学生讲解另两个点的情况。
变式:根据跳水运动中高度随时间变化的函数h(t) = -4.9t 2+6.5t+10图象,估计t=0.4,0.7,1.0时,运动员的瞬时速度(精确到0.1)
师:运动员的瞬时速度,就是高度在此时刻的导数,从图象上看,它表示函数在此点处的切线的斜率。我们可以利用几何画板中的网格估计切线的斜率,从而得到此时刻运动员瞬时速度的近似值。
师进行0.4处瞬时速度的估计运算,做示范,0.7,1.0处的瞬时速度由学生计算。
例2.根据下列条件,分别画出函数图象在这点附近的大致形状。
(1)f(1)=1,f′(1)=-1;
(2)f(-1)=-3,f′(-1)=2;
(3)f(4)=5,f′(4)=0;
师:由导数的几何意义可知,根据题目条件可以画出该点处的切线,从而得到函数图象的大致形状。
师在黑板上画(1)的图象大致形状,做示范,后两个小题由学生相互交流完成。
三.课堂小结
(1)你学到了什么?
(2)你知道了哪些思想方法?
师提问学生,师生共同完成对对本节课内容的归纳总结。并强调“以直代曲”的思想。
四.布置作业
教材10页习题1.1A组第5题,B组第2题。
教学感想
本节课的目标力求使学生体会微积分的基本思想,感受近似与精确的统一,运动和静止的统一,感受量变到质变的转化。在教学过程中,发现了很多不足的地方,这将鞭策我今后不断提高自己,完善自己。
P2
P1
P3
T
C·
EMBED Equation.3
()
Pn
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题:导数的几何意义
海口市琼山中学 郭小兰
教材:人教A版选修2-2
教学目标:
1、知识与技能 :
理解导数的几何意义;
2、过程与方法:
经历导数几何意义的学习过程,体会用导数的几何意义分析图象上点的变化情况的方法。
3、情感态度与价值观:
体会导数与曲线的联系,初步认识数学的科学价值,发展理性思维能力。
教学重点:
理解导数的几何意义;
教学难点:
理解函数的导数就是在某点处的切线的斜率。
教具准备:多媒体课件,三角板。
教学过程:
一、引入新课
师:在前面的学习中,我们知道函数y=f(x)在x=x0处的导数就是函数y=f(x)在x=x0处的瞬时变化率,这是导数的物理意义,那么导数的几何意义是什么呢?我们本节课就来学习导数的几何意义。
板书课题:导数的几何意义
二.讲授新课
教师引导学生观察右图,回答下面问题:
师: 初中平面几何中我们是如何定义圆的切线和割线的?
生:根据直线和圆的交点个数,有一个交点时,直线是圆的切线;
有两个交点时,直线是圆的割线。
师补充说明
1. 圆的切线在点P附近位于圆的一侧(为一般曲线的切线做准备);
2. 当点Pn趋近于点P时,圆的割线PPn趋近于圆的切线PT。当点Pn与点P重合时,割线变成了切线。
师:对于一般曲线的切线和割线,它们又具有怎样的位置关系呢?
探究一:观察一般曲线y=f(x)割线的变化趋势,教师引导学生给出一般曲线的切线定义。
师:过一般曲线上任一点P,我们可以在点P附近类似圆的切线做一条直线PT,使得直线在点P附近位于曲线的一侧,并且与曲线只有一个公共点P。
师:同样的,我们可以在曲线上找另一
点Pn,连接PPn,易知PPn是曲线在点
P处的割线。
师:我们发现,当点Pn趋近于点P时,
割线PPn趋近于确定的位置,这个确定
位置的直线PT叫做曲线在点P处的切线。
探究二:割线的斜率与切线PT的斜率有什么关系?
师:我们首先来看这样一个问题:你能借助图象说说割线PPn的斜率是多少吗?
生:平均变化率。
师继续引导学生发现并说出:
当时,割线PPn切线PT,所以割线PPn的斜率切线PT的斜率。因此,函数y=f(x)在x=x0处的导数等于在该点(x0 ,f(x0))处的切线的斜率,
即 =k。
师板书导数的几何意义。
接下来教师引导学生继续观察:过点P的切线PT最贴近点P附近的曲线y=f(x),因此在点P附近,曲线y=f(x)就可以用过点P的切线PT近似代替。
师:以直代曲是微积分中的重要的思想方法,即以简单的对象(切线)刻画复杂的对象(曲线)。大多数的曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即以直代曲。所以我们就可以在某点附近用曲线的切线相关性质来研究曲线的相关性质。
三 知识运用
例1.如图1.1-3,它表示跳水运动中高度随时间变化的函数h(t) = -4.9t 2+6.5t+10,根据图象,请描述、比较曲线h(t)在t 1、t2、t3附近的变化情况.
解析:借助于几何画板,引导学生运用“以直代曲”的思想由切线斜率的正负得到切线的升降情况,从而得到在切点附近曲线的升降情况。
师引导学生分析题目条件,教师讲解t 1处,然后由学生讲解另两个点的情况。
变式:根据跳水运动中高度随时间变化的函数h(t) = -4.9t 2+6.5t+10图象,估计t=0.4,0.7,1.0时,运动员的瞬时速度(精确到0.1)
师:运动员的瞬时速度,就是高度在此时刻的导数,从图象上看,它表示函数在此点处的切线的斜率。我们可以利用几何画板中的网格估计切线的斜率,从而得到此时刻运动员瞬时速度的近似值。
师进行0.4处瞬时速度的估计运算,做示范,0.7,1.0处的瞬时速度由学生计算。
例2.根据下列条件,分别画出函数图象在这点附近的大致形状。
(1)f(1)=1,f′(1)=-1;
(2)f(-1)=-3,f′(-1)=2;
(3)f(4)=5,f′(4)=0;
师:由导数的几何意义可知,根据题目条件可以画出该点处的切线,从而得到函数图象的大致形状。
师在黑板上画(1)的图象大致形状,做示范,后两个小题由学生相互交流完成。
三.课堂小结
(1)你学到了什么?
(2)你知道了哪些思想方法?
师提问学生,师生共同完成对对本节课内容的归纳总结。并强调“以直代曲”的思想。
四.布置作业
教材10页习题1.1A组第5题,B组第2题。
教学感想
本节课的目标力求使学生体会微积分的基本思想,感受近似与精确的统一,运动和静止的统一,感受量变到质变的转化。在教学过程中,发现了很多不足的地方,这将鞭策我今后不断提高自己,完善自己。
P2
P1
P3
T
C·
EMBED Equation.3
()
Pn
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
