小升初复习精讲精练专题九《解决问题》人教版(复习课件)(共56张PPT)
文档属性
| 名称 | 小升初复习精讲精练专题九《解决问题》人教版(复习课件)(共56张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 13:31:07 | ||
图片预览











文档简介
(共56张PPT)
专题九:解决问题
思维导图
01
归一、归总问题
知识清单
1、归一问题
(1)特征:题中每份的量保持不变,解题时先求出不变的单位量,再求未知量
(2)数量关系:总数量÷份数=单位量 单位量×单位量份数=总数量(正归一)
总数量÷单位量=单位量份数(反归一)
2、归总问题
(1)特征:题中的总量保持不变,解题时先求总量,再求未知量
(2)数量关系:单位量×单位量份数=总数量
02
和差倍问题
知识清单
1、和差问题
(1)特征:已知两个量的和与差,求这两个量
(2)数量关系:(和+差)÷2=较大数 (和-差)÷2=较小数
2、和倍问题
(1)特征:已知两个量的和及两个量的倍数关系,求这两个量
(2)数量关系:和÷(倍数+1)=1倍的量
3、差倍问题
(1)特征:已知两个量的差及两个量的倍数关系,求这两个量
(2)数量关系:差÷(倍数-1)=1倍的量
03
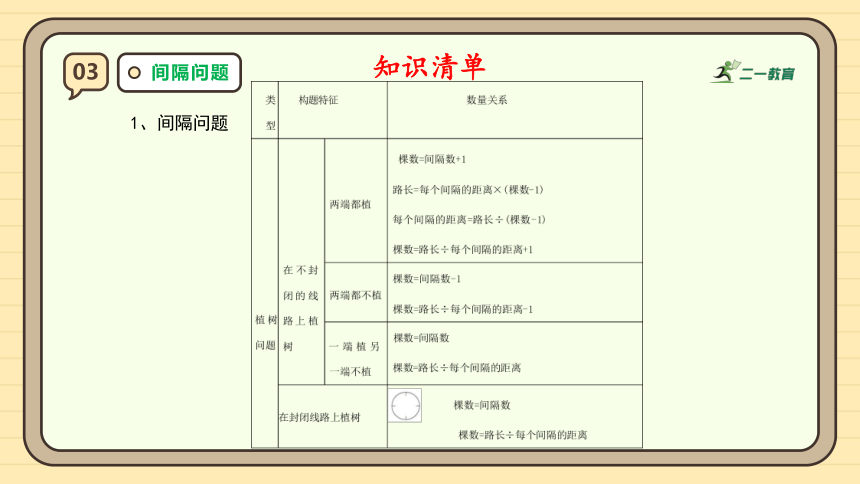
间隔问题
知识清单
1、间隔问题
04
周期问题
知识清单
1、周期问题
(1)周期现象:一组事件或现象按同样的顺序不断重复出现
(2)周期长度:完成这一组事件或现象的时间,一般简称为“周期”
(3)周期问题处理思路:
① 找到重复部分,确定周期长度
② 找到周期现象部分对应的总数
③ 分组:总数÷周期长度=组数……余数
④ 判断所在位置:有余数,余几就代表是组内第几个;无余数,代表是组内最后一个
05
盈亏问题
知识清单
1、盈亏问题
(1)特征:一定数量的物品分成若干份,在不同的分配中,存在有余(盈)、不足(亏)或刚好分完(尽)三种情况
(2)数量关系
⑤ 一盈一尽:盈数÷两次分得之差=份数
⑥ 一亏一尽:亏数÷两次分得之差=份数
⑦ 一盈一亏:(盈数+亏数)÷两次分得之差=份数
⑧ 两次皆亏:(大亏一小亏)÷两次分得之差=份数
⑨ 两次皆盈:(大盈一小盈)÷两次分得之差=份数
06
鸡兔同笼
知识清单
1、鸡兔同笼
(1)特征:已知鸡与兔的总头数和总足数,求鸡与兔各有多少只。 一般可用列表、假设等方法解答
(2)数量关系
① 假设全是鸡,则有:兔的只数=(总足数-2×总头数)÷2
鸡的只数=总头数-兔的只数
② 假设全是兔,则有:鸡的只数=(4×总头数-总足数)÷2
兔的只数=总头数-鸡的只数
07
牛吃草
知识清单
1、牛吃草问题
(1)草的生长速度=(对应的牛头数×吃的较多天数-相应的牛头数×吃的较少天数)÷(吃的较多天数-吃的较少天数)
(2)原有草量=牛头数×吃的天数-草的生长速度×吃的天数
(3)吃的天数=原有草量÷(牛头数-草的生长速度)
(4)牛头数=原有草量÷吃的天数+草的生长速度
08
行程问题
知识清单
1、行程问题
(1)速度×时间=路程
(2)路程÷时间=速度
(3)路程÷速度=时间
09
工程问题
知识清单
1、工程问题
(1)工作效率×工作时间=工作总量
(2)工作总量÷工作时间=工作效率
(3)工作总量÷工作效率=工作时间
10
浓度问题
知识清单
1、浓度问题
(1)溶液=溶质+溶剂
(2)浓度=溶质÷溶液×100%
(3)溶质=溶液×浓度
(4)溶液=溶质÷浓度
11
利率、利税
知识清单
1、利率、利税
(1)收入中应纳税部分×税率剂=应纳税额
(2)利息=本金×利率×存期
(3)本息和=本金+利息
(4)利率=利息÷存期÷本金×100%
(5)税后利息=利息-利息的应纳税额=利息-利息×利息税率=利息×(1-利息税率)
(6)税后利息=本金×利率×时间×(1-利息税率)
12
折扣、利润、购物方案
知识清单
1、折扣问题
(1)现价÷原价=折扣
(2)原价×折扣=现价
(3)现价÷折扣=原价
2、利润问题
(1)售价-成本=利润
(2)售价-利润=成本
(3)成本+利润=售价
12
折扣、利润、购物方案
知识清单
3、价格问题
(1)单价×数量=总价
(2)总价÷数量=单价
(3)总价÷单价=数量
13
分段计费
知识清单
1、分段计费
(1)出租车=起步价+(总路程-起步路程)×单价
(2)水费=第一档量×单价1+第二档量×单价2+……
(3)照相费=拍照定价+加印照片数量×单价
(4)邮费=首重费用+续重费用
14
题型训练
例题精讲
01 归一、归总问题
1.一辆汽车从甲地开往乙地,前3小时行了168千米,照这样的速度,又行了5小时,正好到达乙地。甲、乙两地相距多少千米?
【答案】448千米
【解答】解法一:汽车的速度:168÷3=56千米/时
甲、乙两地相距:56×(3+5)=448千米
解法二:汽车的速度:168÷3=56千米/时
甲、乙两地相距:168+56×5=448千米
答:甲、乙两地相距448千米。
14
题型训练
例题精讲
01 归一、归总问题
2.一个居民小区计划安排40名工人,用两周时间铺设完天然气管道。工人工作了2天后,又增加了20人,若每个工人的工作效率相同,这个小区的居民可以提前几天用上天然气?
【答案】4天
【解答】工作总量:40×7×2=560
完成剩下的工作量还需要的天数:(560-40×2)÷(40+20)=8天
提前时间:14-2-8=4天
答:这个小区的居民可以提前4天用上天然气。
14
题型训练
例题精讲
02 和差倍问题
1.甲站原有车52辆,乙站原有车32辆,若每天从甲站开往乙站28辆,从乙站开往甲站24辆,几天后乙站车辆数是甲站的2倍?
【答案】6天
【解答】(52+32)÷(2+1)=28辆
(52-28)÷(28-24)=6天
答:6天后乙站车辆数是甲站的2倍。
14
题型训练
例题精讲
02 和差倍问题
2.有甲乙丙三袋化肥,甲乙两袋共重34千克,乙丙两袋共重32千克,甲丙两袋共重22千克,求三袋化肥各重多少千克?
【答案】甲袋化肥重12千克,丙袋化肥重10千克,乙袋化肥重22千克
【解答】甲袋:(22+2)÷2=12千克 丙袋:(22-2)÷2=10千克
乙袋:34-12=22千克
答:甲袋化肥重12千克,丙袋化肥重10千克,乙袋化肥重22千克。
14
题型训练
例题精讲
03 间隔问题
1.从南镇到北镇的路的一边共有27根电线杆,相邻两根电线杆之间的距离是30米,现在要重新修改,除两端的2根不动,其余的要拆除,重新在中间竖19根。这时相邻两根电线杆之间的平均距离是多少米?
【答案】39米
【解答】30×(27-1)
=30×26
=780(米)
780÷(19+1)
=780÷20
=39(米)
答:这时相邻两根电线杆之间的平均距离是39米。
14
题型训练
例题精讲
03 间隔问题
2.一个街心花园如下图所示,它由四个大小相等的等边三角形组成,已知从每个小三角形的顶点开始,到下一个顶点均匀栽有10棵花,大三角形边上栽有多少棵花?中间的小三角形边上共栽有多少棵花?
【答案】54棵 27棵
【解答】大三角形边上共栽花:
(10×2-1-1)×3
=18×3
=54(棵)
中间小三角形边上共栽花:
(10-1)×3
=9×3
=27(棵) 答:大三角形边上栽有54棵花,中间小三角形边上共栽有27棵花。
14
题型训练
例题精讲
04 周期问题
1.鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪12种动物依次代表各年,如果公元1年是鸡年,那么公元2025年是什么年?
【答案】蛇年
【解答】2025÷12=168……9
答:公元2025年是蛇年。
14
题型训练
例题精讲
04 周期问题
2.节日的夜景真漂亮,街上的彩灯按照5盏红灯、4盏蓝灯、3盏黄灯,然后又是5盏红灯、4盏蓝灯、3盏黄灯这样排下去。(1)第100盏灯是什么颜色?(2)前150盏灯中有多少盏蓝灯?
【答案】(1)红灯 (2)49盏
【解答】(1)100÷12=8个……4盏
答:第100盏灯是红灯。
(2)150÷12=12个……6盏 12×4=48盏 48+1=49盏
答:前150盏灯中有49盏蓝灯。
14
题型训练
例题精讲
05 盈亏问题
1.妈妈去菜市场买猪肉,买5斤猪肉剩余5元钱,买6斤差3元钱。猪肉每斤多少钱?妈妈带了多少钱?
【答案】猪肉每斤8元,妈妈带了45元
【解答】猪肉价格:(5+3)÷(6-5)=8元
妈妈带了:5×8+5=45元或8×6-3=45元
答:猪肉每斤8元,妈妈带了45元。
14
题型训练
例题精讲
05 盈亏问题
2.饲养员将一堆桃子分给一群猴子。如果每只猴子分10个桃子,则缺24个桃子;如果每只猴子分8个桃子,则缺2个桃子。猴子有多少只?这堆桃子有多少个?
【答案】猴子有11只,这堆桃子有86个
【解答】猴子只数:(24-2)÷(10-8)=11只
桃子个数:11×10-24=86个
答:猴子有11只,这堆桃子有86个。
14
题型训练
例题精讲
06 鸡兔同笼
1.蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀(小翅膀不计)。现有三种动物共18只,共有112条腿和22对翅膀。蜘蛛、蜻蜓、蝉各有多少只?
【答案】蜘蛛2只;蜻蜓6只;蝉10只
【解答】18×6=108(条) 112-108=4(条) 8-6=2(条)
蜘蛛:4÷2=2(只)
18-2=16(只)
16×2=32(对)
32-22=10(对)
2-1=1(对)
蝉:10÷1=10(只)
蜻蜓:16-10=6(只)
答:蜘蛛2只,蜻蜓6只,蝉10只。
14
题型训练
例题精讲
06 鸡兔同笼
2.学校乒乓球室有20张乒乓球台,现在共有54人在打球,那么正在进行乒乓球单打比赛和双打比赛的乒乓球台各有多少张?
【答案】单打13张;双打7张
【解答】20×4=80(人)
80-54=26(人)
4-2=2(人)
单打:26÷2=13(张)
双打:20-13=7(张)
答:乒乓球单打比赛有13张,双打比赛的乒乓球台有7张。
14
题型训练
例题精讲
07 牛吃草问题
1.由于天气逐渐变冷,有一片牧场上的草每天都在匀速地减少,如果12头牛来吃草,8天可以把草地上的草吃光,如果17头牛来吃草6天可以把草地的草吃光,如果现在有27头牛来吃草,几天后可以把牧场上的草吃光?
【答案】4天
【解答】设每天每头牛吃草1份,
(17×6-12×8)÷(8-6)
=6÷2
=3(份)
17×6+6×3
=102+18
=120(份)
120÷(27+3)
=120÷30
=4(天)
答:如果现在有27头牛来吃草,4天后可以把牧场上的草吃光。
14
题型训练
例题精讲
07 牛吃草问题
2.某车站在检票前若干分钟就开始排队,每分钟新来的旅客人数一样多,从开始检票到等候检票的队伍排完,同时开4个检票口需3分钟,同时开5个检票口需2分钟。如果想要在1.5分钟后使等候的队伍排完,需要同时开几个检票口?
【答案】6个
【解答】(4×3-5×2)÷(3-2)
=2÷1
=2
4×3-2×3
=12-6
=6
(6+2×1.5)÷1.5
=9÷1.5
=6(个)
答:需要同时开6个检票口。
14
题型训练
例题精讲
08 行程问题
1.甲、乙两辆汽车同时从东西两城相向开出,甲车每小时行60千米,乙车每小时行56千米,两车在距中点16千米处相遇。东西两城相距多少千米?
【答案】928千米
【解答】(60+56)×[(16×2)÷(60-56)]
=116×(32÷4)
=116×8
=928(千米)
答:东西两城相距928千米。
14
题型训练
例题精讲
08 行程问题
2.甲、乙两地相距360千米,一辆汽车原计划用8小时从甲地到乙地,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生了故障,在途中停留了1小时。如果按照原定的时间到达乙地,汽车在后一半路程上每小时应该行驶多少千米?
【答案】45千米;60千米
【解答】360÷8=45(千米/小时);
360÷2=180(千米)
8÷2=4(小时)
8-(4+1)=3(小时)
180÷3=60(千米/小时)
答:汽车每小时应该行驶45千米,汽车在后一半路程上每小时应该行驶60千米。
14
题型训练
例题精讲
09 工程问题
1.某区为了改善城市风貌,现请来176名工人擦洗各个天桥的护栏,如果在规定时间内平均每人擦洗18米,各个天桥的护栏长度一共是3000米,这些工人能按时完成任务吗?
【答案】能
【解答】176×18=3168(米)
3168米>3000米
答:这些工人能按时完成任务。
14
题型训练
例题精讲
09 工程问题
2.高德工程队维修一条乡村公路,原计划每天修路180米,15天可以完成。因工作需要,要求9天完成,实际平均每天修路多少米?
【答案】300米
【解答】180×15÷9
=2700÷9
=300(米)
答:实际平均每天修路300米。
14
题型训练
例题精讲
10 浓度问题
1.有浓度是20%的盐水溶液若干千克,如果再加入20千克盐,那么盐水的浓度就变为30%,原来的盐水是( )千克。
【答案】140千克
【解答】解:设原来的盐水有x千克。
(x+20)×30%=20%x+20
0.3x+6=0.2x+20
0.3x+6-0.2x=20
0.1x+6=20
0.1x=20-6
0.1x=14
x=14÷0.1
x=140 原来的盐水是140千克。
14
题型训练
例题精讲
10 浓度问题
2.甲容器中有20%的盐水300克,乙容器中有25%的盐水200克。往甲、乙两容器中分别倒入等量的水,使两个容器中的盐水浓度一样。每个容器应倒入水多少克?
【答案】300克
【解答】300×20%=60(克)
200×25%=50(克)
60∶50
=(60÷10)∶(50÷10)
=6∶5
(300-200)÷(6-5)
=100÷1
=100(克)
6×100=600(克) 600-300=300(克) 答:每个容器应倒入水300克。
14
题型训练
例题精讲
11 利率、利税问题
1.某个体粮油经销店年初向赵先生借款500元,年利率为12%。第一年末还280元,第二年末赵先生到经销店购买10千克精制香油(折合成现金作为还款资金),第三年末又还207.20元,全都还清。每千克香油的价钱是多少元?
【答案】12.86元
【解答】第一年末还款后,还剩下款数为
500×(1+12%)-280
=500×1.12-280
=280(元)。
第二年末应还款数为
280×(1+12%)
=280×1.12
=313.6(元)。
第二年末购油后,还剩欠款数
207.20÷(1+12%)
=207.20÷1.12
=185(元)。
10千克香油需要的钱数为313.6-185=128.6(元)。
所以,每千克香油价格为128.6÷10=12.86(元)。
答:每千克香油的价格是12.86元。
14
题型训练
例题精讲
11 利率、利税问题
2.国家规定个人发表文章,出版图书获得稿费的计算方法是:①稿费不高于800元的不纳税;②稿费高于800元又不高于4000元的应缴纳超过800元的那一部分的14%的税;③稿费高于4000元的应缴纳全部稿费的11%的税。今得知丁老师获得一笔稿费,并且依法缴纳个人所得税420元,问丁老师这笔稿费是多少元?又得知马老师获得一笔稿费,并且依法缴纳个人所得税550元,问马老师这笔稿费是多少元?
【答案】丁老师的稿费为3800元,马老师的稿费为5000元
【解答】第一档的不纳税,第二档的要纳税
(4000-800)×14%
=3200×14%
=448(元)
说明丁老师稿费低于4000元。
丁老师的稿费为:
420÷14%+800
=3000+800
=3800(元)。
马老师的所得税高于448元,应该用第三档的来计算。
马老师的稿费为:550÷11%=5000(元)。
答:丁老师的稿费为3800元,马老师的稿费为5000元。
14
题型训练
例题精讲
12 折扣、利润、购物方案
1.某人到商品买红、蓝两种笔,红笔定价5元,蓝笔定价9元.由于买的数量较多,商店就给打折扣.红笔按定价 85%出售,蓝笔按定价 80%出售.结果他付的钱就少了18%.已知他买了蓝笔 30支,问红笔买了几支?
【答案】36支
【解答】相当于把两种折扣的百分数配比,成为1-18%=82%.
(85%-82%)∶(82%-80%)=3∶2.
他买红、蓝两种笔的钱数之比是2∶3.
设买红笔是x支,可列出比例式
5x∶9×30=2∶3
x==36(支)
答:红笔买了 36支。
14
题型训练
例题精讲
12 折扣、利润、购物方案
2.某商店到水果产地去收购橘子,收购价为每千克1.20元。从产地到商店的距离是400千米,运费为每吨货物每运1千米收1.50元。如果在运输及销售过程中的损耗是10%,商店要想实现25%的利润率,零售价应是每千克多少元?
【答案】2.50元
【解答】每千克的运费是1.50×400÷1000=0.60(元)
每千克的成本:
(1.20+0.60)÷(1-10%)
=1.8÷0.9
=2.00(元)
零售价为:2.00×(25%+1)
=2×1.25
=2.50(元) 答:零售价应是每千克2.50元。
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(1)若小明家某月用水18立方米,则小明家该月实际应交水费多少元?
【答案】95.5元
【解答】(1)根据题意得:15×4.5+(18-15)×6+10
=15×4.5+3×6+10
=67.5+18+10
=95.5(元)。
答:小明家该月实际应交水费95.5元;
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(2)已知某户居民某月的实际应交水费为187.5元,则这户居民的该月用水量是多少立方米?
【答案】30立方米
【解答】设这户居民的该月用水量是x立方米,
∵15×4.5+(20-15)×6+10=107.5,107.5<187.5 ∴x>20
根据题意得:15×4.5+(20-15)×6+8(x-20)+10=187.5,
解得:x=30 答:这户居民的该月用水量是30立方米;
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(3)若某户某月实际应交水费平均每立方米6.5元,求该户该月用水量。
【答案】5或35立方米
【解答】设该户该月用水量是y立方米,
当0<y≤15时,4.5y+10=6.5y,解得:y=5;
当15<y≤20时,15×4.5+6(y-15)+10=6.5y,解得:y=﹣25(不符合题意,舍去);
当y>20时,15×4.5+(20-15)×6+8(y-20)+10=6.5y,解得:y=35
答:该户该月用水量是5或35立方米。
14
题型训练
例题精讲
13 分段计费
2.某市出租车规定:
有一天,小红一家三人坐出租车去离家8千米远的动物园玩,动物园每张门票是58元,每人还买了一瓶1.5元的矿泉水。问小红一家共花费了多少元?
【答案】193.5元
【解答】打车费用:8+1.4×(8-3)
=8+1.4×5
=8+7
=15(元)
总费用:58×3+1.5×3+15
=174+4.5+15
=178.5+15
=193.5(元) 答:小红一家共花费了193.5元。
15
专项训练
专项练习
1.陈师傅原来每天最多能加工150个零件。自从工厂引进新设备后,陈师傅每天加工的零件个数在170~200个之间(含200个)。现在陈师傅1个月(按22天计算)最多能加工( )个零件。
2.过年了,同学们要亲手做一些工艺品送给敬老院的老人,开始时艺术小组的同学们先做一天,随后增加15位同学和他们一起又做了两天,恰好完成,假设每位同学的工作效率相同,且一位同学单独完成需要60天,那么艺术小组的同学有 ( )位。
4400
10
15
专项训练
专项练习
3.污水处理厂有600吨污水待处理,且每天新增同样多的污水需要处理,如果每天处理200吨,6天可以处理完。如果每天处理250吨,( )天可以处理完。
4.春节前夕,一个富翁向乞丐帮帮众施舍一笔钱财。一开始他准备给每人100元,结果剩下350元。他决定每人多给20元。这时从其他地方有闻讯赶来了5个乞丐,如果他们每个人拿到的钱也和其他乞丐一样多,富翁还需要再增加550元。富翁原打算施舍( )元。
4
1850
15
专项训练
专项练习
5.在一个庆典晚会上,男女嘉宾共69人。出现了一个非常有趣的情况:每位女士认识的男士的人数各不相同,而且组成连续的自然数,最少的认识16位男士,最多的只有两位男士不认识。这次晚会上,共有女嘉宾( )人。
6.假期将至,超市都在搞打折促销活动,同一品牌原价为50元的洗衣液,甲超市打七折销售,乙超市降价20%销售,丙超市“买三送一”。现在妈妈打算买4瓶洗衣液,在( )超市买更划算。
A.甲 B.乙 C.丙
26
A
15
专项训练
专项练习
7.数学竞赛共10道题,做对一题得8分,做错一题(或不做)倒扣5分,小明得41分,他共做错(或不做)了( )道题。
A.2 B.3 C.4 D.5
8.希望小学学生排成正方形方阵做早操,从前往后数小明排第7个,从后往前数排第13个,从左往右数,从右往左数都排第10个。最外层一共可以排( )个学生。
A.78 B.72 C.76 D.80
B
B
15
专项训练
专项练习
9.下列问题中,能用90-21×3解决的是( )。
①篮球每个90元,垒球每个21元,一个篮球比3个垒球贵多少元?
②工程队翻修一条90千米的路,每天修21千米,3天后还剩多少?
③篮球原价90元,现降价21元。买3个能省多少钱?
④轿车每小时行90千米,卡车每小时比它少行21千米。卡车从甲地到乙地用了3小时,甲乙两地相距多少千米?
A.①② B.③④ C.①②③ D.①②③④
10.小明调制了3杯蜂蜜水,最甜的是( )。
A.用10克蜂蜜配成110克蜂蜜水。
B.蜂蜜与水的比是1:10。
C.蜂蜜占蜂蜜水的10%。
A
C
15
专项训练
专项练习
11.李英和黄明比赛走楼梯,李英走3级楼梯时,黄明能走5级,这幢楼每两层之间有20级楼梯,那么当黄明走到6楼时,李英走到几楼?
李英、黄明的速度比=3∶5
相同时间内。速度和路程成正比
所以,李英和黄明的路程比=3∶5
当黄明走到6楼时,李英走到了:(6-1)÷5×3+1=4楼
答:当黄明走到6楼时,李英走到4楼。
15
专项训练
专项练习
12.标有A、B、C、D、E、F的6盏灯依次排成一行,每盏灯有一个开关。现在A、C、E不亮,其余3盏亮着。军军从灯A开始顺次拉动开关,即从A到F,再从A开始顺次拉动开关,他这样拉动1000次开关后,哪些灯亮着,哪些灯不亮?
1000÷6=166……4,意味着6盏灯从A到F被拉动166个循环后,A、B、C、D又被拉动各一次。因此,灯A,B,C,D各被拉动167次开关,灯E,F各被拉动166次开关。初始状态A、C、E不亮,B、D、F亮着,所以灯A,B,C,D改变了原来状态,灯E,F没改变原来状态。
故当军军拉动1000次后A,C,F亮,而B,D,E没亮。
15
专项训练
专项练习
13.欣欣、希希、望望三人分别在相距18千米的A、B两地同时动身,欣欣、希希二人从A地出发,步行去B地,望望从B地出发向,骑自行车去A地,望望首先在途中与希希相遇,10分钟后又与欣欣相遇,然后继续前进,达到A地后立马掉头返回B地,在AB的中点追上了欣欣,最后与希希同时到达B地。三人每分钟各行多少米?
18÷(1+2)×2
=18÷3×2
=6×2
=12(千米)
12÷3=4(千米)
18-12-4
=6-4
=2(千米)
=2000米
2000÷10=200(米)
200÷(1+3)
=200÷4
=50(米)
50×3=150(米)
150÷2=75(米)
答:欣欣每分钟行50米,希希每分钟行75米,望望每分钟行150米。
15
专项训练
专项练习
14.某汽车公司组织比赛,比赛规则如图所示:维修队有29人(含司机),速度为每分钟1千米(不计掉头时间),则维修队完成比赛最快需多少时间?
10÷1=10(分钟)
10×2=20(分钟)
29=4×6+5
20×6+10
=120+10
=130(分钟)
答:维修队完成比赛最快需130分钟。
15
专项训练
专项练习
15.某学校举办数学夏令营活动,由5名老师带领若干名学生参加,学校联系了两家标价相同的旅行社(每名老师和每名学生的费用也相同)。经过商议后,甲旅行社给出的优惠是:老师的费用按原价,学生的费用打七折;乙旅行社给出的优惠是:老师、学生的费用全部打八折。经过计算,甲旅行社优惠后的总费用比乙旅行社优惠后的总费用便宜10%,那么学生有多少名?
解:设学生有x名,每人100元。
500+100x×70%=100(x+5)×80%×(1-10%)
500+70x=80(x+5)×90%
500+70x=72(x+5)
500+70x=72x+360
72x-70x=500-360
2x=140
x=140÷2
x=70
答:学生有70名。
https://www.21cnjy.com/recruitment/home/fine
专题九:解决问题
思维导图
01
归一、归总问题
知识清单
1、归一问题
(1)特征:题中每份的量保持不变,解题时先求出不变的单位量,再求未知量
(2)数量关系:总数量÷份数=单位量 单位量×单位量份数=总数量(正归一)
总数量÷单位量=单位量份数(反归一)
2、归总问题
(1)特征:题中的总量保持不变,解题时先求总量,再求未知量
(2)数量关系:单位量×单位量份数=总数量
02
和差倍问题
知识清单
1、和差问题
(1)特征:已知两个量的和与差,求这两个量
(2)数量关系:(和+差)÷2=较大数 (和-差)÷2=较小数
2、和倍问题
(1)特征:已知两个量的和及两个量的倍数关系,求这两个量
(2)数量关系:和÷(倍数+1)=1倍的量
3、差倍问题
(1)特征:已知两个量的差及两个量的倍数关系,求这两个量
(2)数量关系:差÷(倍数-1)=1倍的量
03
间隔问题
知识清单
1、间隔问题
04
周期问题
知识清单
1、周期问题
(1)周期现象:一组事件或现象按同样的顺序不断重复出现
(2)周期长度:完成这一组事件或现象的时间,一般简称为“周期”
(3)周期问题处理思路:
① 找到重复部分,确定周期长度
② 找到周期现象部分对应的总数
③ 分组:总数÷周期长度=组数……余数
④ 判断所在位置:有余数,余几就代表是组内第几个;无余数,代表是组内最后一个
05
盈亏问题
知识清单
1、盈亏问题
(1)特征:一定数量的物品分成若干份,在不同的分配中,存在有余(盈)、不足(亏)或刚好分完(尽)三种情况
(2)数量关系
⑤ 一盈一尽:盈数÷两次分得之差=份数
⑥ 一亏一尽:亏数÷两次分得之差=份数
⑦ 一盈一亏:(盈数+亏数)÷两次分得之差=份数
⑧ 两次皆亏:(大亏一小亏)÷两次分得之差=份数
⑨ 两次皆盈:(大盈一小盈)÷两次分得之差=份数
06
鸡兔同笼
知识清单
1、鸡兔同笼
(1)特征:已知鸡与兔的总头数和总足数,求鸡与兔各有多少只。 一般可用列表、假设等方法解答
(2)数量关系
① 假设全是鸡,则有:兔的只数=(总足数-2×总头数)÷2
鸡的只数=总头数-兔的只数
② 假设全是兔,则有:鸡的只数=(4×总头数-总足数)÷2
兔的只数=总头数-鸡的只数
07
牛吃草
知识清单
1、牛吃草问题
(1)草的生长速度=(对应的牛头数×吃的较多天数-相应的牛头数×吃的较少天数)÷(吃的较多天数-吃的较少天数)
(2)原有草量=牛头数×吃的天数-草的生长速度×吃的天数
(3)吃的天数=原有草量÷(牛头数-草的生长速度)
(4)牛头数=原有草量÷吃的天数+草的生长速度
08
行程问题
知识清单
1、行程问题
(1)速度×时间=路程
(2)路程÷时间=速度
(3)路程÷速度=时间
09
工程问题
知识清单
1、工程问题
(1)工作效率×工作时间=工作总量
(2)工作总量÷工作时间=工作效率
(3)工作总量÷工作效率=工作时间
10
浓度问题
知识清单
1、浓度问题
(1)溶液=溶质+溶剂
(2)浓度=溶质÷溶液×100%
(3)溶质=溶液×浓度
(4)溶液=溶质÷浓度
11
利率、利税
知识清单
1、利率、利税
(1)收入中应纳税部分×税率剂=应纳税额
(2)利息=本金×利率×存期
(3)本息和=本金+利息
(4)利率=利息÷存期÷本金×100%
(5)税后利息=利息-利息的应纳税额=利息-利息×利息税率=利息×(1-利息税率)
(6)税后利息=本金×利率×时间×(1-利息税率)
12
折扣、利润、购物方案
知识清单
1、折扣问题
(1)现价÷原价=折扣
(2)原价×折扣=现价
(3)现价÷折扣=原价
2、利润问题
(1)售价-成本=利润
(2)售价-利润=成本
(3)成本+利润=售价
12
折扣、利润、购物方案
知识清单
3、价格问题
(1)单价×数量=总价
(2)总价÷数量=单价
(3)总价÷单价=数量
13
分段计费
知识清单
1、分段计费
(1)出租车=起步价+(总路程-起步路程)×单价
(2)水费=第一档量×单价1+第二档量×单价2+……
(3)照相费=拍照定价+加印照片数量×单价
(4)邮费=首重费用+续重费用
14
题型训练
例题精讲
01 归一、归总问题
1.一辆汽车从甲地开往乙地,前3小时行了168千米,照这样的速度,又行了5小时,正好到达乙地。甲、乙两地相距多少千米?
【答案】448千米
【解答】解法一:汽车的速度:168÷3=56千米/时
甲、乙两地相距:56×(3+5)=448千米
解法二:汽车的速度:168÷3=56千米/时
甲、乙两地相距:168+56×5=448千米
答:甲、乙两地相距448千米。
14
题型训练
例题精讲
01 归一、归总问题
2.一个居民小区计划安排40名工人,用两周时间铺设完天然气管道。工人工作了2天后,又增加了20人,若每个工人的工作效率相同,这个小区的居民可以提前几天用上天然气?
【答案】4天
【解答】工作总量:40×7×2=560
完成剩下的工作量还需要的天数:(560-40×2)÷(40+20)=8天
提前时间:14-2-8=4天
答:这个小区的居民可以提前4天用上天然气。
14
题型训练
例题精讲
02 和差倍问题
1.甲站原有车52辆,乙站原有车32辆,若每天从甲站开往乙站28辆,从乙站开往甲站24辆,几天后乙站车辆数是甲站的2倍?
【答案】6天
【解答】(52+32)÷(2+1)=28辆
(52-28)÷(28-24)=6天
答:6天后乙站车辆数是甲站的2倍。
14
题型训练
例题精讲
02 和差倍问题
2.有甲乙丙三袋化肥,甲乙两袋共重34千克,乙丙两袋共重32千克,甲丙两袋共重22千克,求三袋化肥各重多少千克?
【答案】甲袋化肥重12千克,丙袋化肥重10千克,乙袋化肥重22千克
【解答】甲袋:(22+2)÷2=12千克 丙袋:(22-2)÷2=10千克
乙袋:34-12=22千克
答:甲袋化肥重12千克,丙袋化肥重10千克,乙袋化肥重22千克。
14
题型训练
例题精讲
03 间隔问题
1.从南镇到北镇的路的一边共有27根电线杆,相邻两根电线杆之间的距离是30米,现在要重新修改,除两端的2根不动,其余的要拆除,重新在中间竖19根。这时相邻两根电线杆之间的平均距离是多少米?
【答案】39米
【解答】30×(27-1)
=30×26
=780(米)
780÷(19+1)
=780÷20
=39(米)
答:这时相邻两根电线杆之间的平均距离是39米。
14
题型训练
例题精讲
03 间隔问题
2.一个街心花园如下图所示,它由四个大小相等的等边三角形组成,已知从每个小三角形的顶点开始,到下一个顶点均匀栽有10棵花,大三角形边上栽有多少棵花?中间的小三角形边上共栽有多少棵花?
【答案】54棵 27棵
【解答】大三角形边上共栽花:
(10×2-1-1)×3
=18×3
=54(棵)
中间小三角形边上共栽花:
(10-1)×3
=9×3
=27(棵) 答:大三角形边上栽有54棵花,中间小三角形边上共栽有27棵花。
14
题型训练
例题精讲
04 周期问题
1.鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪12种动物依次代表各年,如果公元1年是鸡年,那么公元2025年是什么年?
【答案】蛇年
【解答】2025÷12=168……9
答:公元2025年是蛇年。
14
题型训练
例题精讲
04 周期问题
2.节日的夜景真漂亮,街上的彩灯按照5盏红灯、4盏蓝灯、3盏黄灯,然后又是5盏红灯、4盏蓝灯、3盏黄灯这样排下去。(1)第100盏灯是什么颜色?(2)前150盏灯中有多少盏蓝灯?
【答案】(1)红灯 (2)49盏
【解答】(1)100÷12=8个……4盏
答:第100盏灯是红灯。
(2)150÷12=12个……6盏 12×4=48盏 48+1=49盏
答:前150盏灯中有49盏蓝灯。
14
题型训练
例题精讲
05 盈亏问题
1.妈妈去菜市场买猪肉,买5斤猪肉剩余5元钱,买6斤差3元钱。猪肉每斤多少钱?妈妈带了多少钱?
【答案】猪肉每斤8元,妈妈带了45元
【解答】猪肉价格:(5+3)÷(6-5)=8元
妈妈带了:5×8+5=45元或8×6-3=45元
答:猪肉每斤8元,妈妈带了45元。
14
题型训练
例题精讲
05 盈亏问题
2.饲养员将一堆桃子分给一群猴子。如果每只猴子分10个桃子,则缺24个桃子;如果每只猴子分8个桃子,则缺2个桃子。猴子有多少只?这堆桃子有多少个?
【答案】猴子有11只,这堆桃子有86个
【解答】猴子只数:(24-2)÷(10-8)=11只
桃子个数:11×10-24=86个
答:猴子有11只,这堆桃子有86个。
14
题型训练
例题精讲
06 鸡兔同笼
1.蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀(小翅膀不计)。现有三种动物共18只,共有112条腿和22对翅膀。蜘蛛、蜻蜓、蝉各有多少只?
【答案】蜘蛛2只;蜻蜓6只;蝉10只
【解答】18×6=108(条) 112-108=4(条) 8-6=2(条)
蜘蛛:4÷2=2(只)
18-2=16(只)
16×2=32(对)
32-22=10(对)
2-1=1(对)
蝉:10÷1=10(只)
蜻蜓:16-10=6(只)
答:蜘蛛2只,蜻蜓6只,蝉10只。
14
题型训练
例题精讲
06 鸡兔同笼
2.学校乒乓球室有20张乒乓球台,现在共有54人在打球,那么正在进行乒乓球单打比赛和双打比赛的乒乓球台各有多少张?
【答案】单打13张;双打7张
【解答】20×4=80(人)
80-54=26(人)
4-2=2(人)
单打:26÷2=13(张)
双打:20-13=7(张)
答:乒乓球单打比赛有13张,双打比赛的乒乓球台有7张。
14
题型训练
例题精讲
07 牛吃草问题
1.由于天气逐渐变冷,有一片牧场上的草每天都在匀速地减少,如果12头牛来吃草,8天可以把草地上的草吃光,如果17头牛来吃草6天可以把草地的草吃光,如果现在有27头牛来吃草,几天后可以把牧场上的草吃光?
【答案】4天
【解答】设每天每头牛吃草1份,
(17×6-12×8)÷(8-6)
=6÷2
=3(份)
17×6+6×3
=102+18
=120(份)
120÷(27+3)
=120÷30
=4(天)
答:如果现在有27头牛来吃草,4天后可以把牧场上的草吃光。
14
题型训练
例题精讲
07 牛吃草问题
2.某车站在检票前若干分钟就开始排队,每分钟新来的旅客人数一样多,从开始检票到等候检票的队伍排完,同时开4个检票口需3分钟,同时开5个检票口需2分钟。如果想要在1.5分钟后使等候的队伍排完,需要同时开几个检票口?
【答案】6个
【解答】(4×3-5×2)÷(3-2)
=2÷1
=2
4×3-2×3
=12-6
=6
(6+2×1.5)÷1.5
=9÷1.5
=6(个)
答:需要同时开6个检票口。
14
题型训练
例题精讲
08 行程问题
1.甲、乙两辆汽车同时从东西两城相向开出,甲车每小时行60千米,乙车每小时行56千米,两车在距中点16千米处相遇。东西两城相距多少千米?
【答案】928千米
【解答】(60+56)×[(16×2)÷(60-56)]
=116×(32÷4)
=116×8
=928(千米)
答:东西两城相距928千米。
14
题型训练
例题精讲
08 行程问题
2.甲、乙两地相距360千米,一辆汽车原计划用8小时从甲地到乙地,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生了故障,在途中停留了1小时。如果按照原定的时间到达乙地,汽车在后一半路程上每小时应该行驶多少千米?
【答案】45千米;60千米
【解答】360÷8=45(千米/小时);
360÷2=180(千米)
8÷2=4(小时)
8-(4+1)=3(小时)
180÷3=60(千米/小时)
答:汽车每小时应该行驶45千米,汽车在后一半路程上每小时应该行驶60千米。
14
题型训练
例题精讲
09 工程问题
1.某区为了改善城市风貌,现请来176名工人擦洗各个天桥的护栏,如果在规定时间内平均每人擦洗18米,各个天桥的护栏长度一共是3000米,这些工人能按时完成任务吗?
【答案】能
【解答】176×18=3168(米)
3168米>3000米
答:这些工人能按时完成任务。
14
题型训练
例题精讲
09 工程问题
2.高德工程队维修一条乡村公路,原计划每天修路180米,15天可以完成。因工作需要,要求9天完成,实际平均每天修路多少米?
【答案】300米
【解答】180×15÷9
=2700÷9
=300(米)
答:实际平均每天修路300米。
14
题型训练
例题精讲
10 浓度问题
1.有浓度是20%的盐水溶液若干千克,如果再加入20千克盐,那么盐水的浓度就变为30%,原来的盐水是( )千克。
【答案】140千克
【解答】解:设原来的盐水有x千克。
(x+20)×30%=20%x+20
0.3x+6=0.2x+20
0.3x+6-0.2x=20
0.1x+6=20
0.1x=20-6
0.1x=14
x=14÷0.1
x=140 原来的盐水是140千克。
14
题型训练
例题精讲
10 浓度问题
2.甲容器中有20%的盐水300克,乙容器中有25%的盐水200克。往甲、乙两容器中分别倒入等量的水,使两个容器中的盐水浓度一样。每个容器应倒入水多少克?
【答案】300克
【解答】300×20%=60(克)
200×25%=50(克)
60∶50
=(60÷10)∶(50÷10)
=6∶5
(300-200)÷(6-5)
=100÷1
=100(克)
6×100=600(克) 600-300=300(克) 答:每个容器应倒入水300克。
14
题型训练
例题精讲
11 利率、利税问题
1.某个体粮油经销店年初向赵先生借款500元,年利率为12%。第一年末还280元,第二年末赵先生到经销店购买10千克精制香油(折合成现金作为还款资金),第三年末又还207.20元,全都还清。每千克香油的价钱是多少元?
【答案】12.86元
【解答】第一年末还款后,还剩下款数为
500×(1+12%)-280
=500×1.12-280
=280(元)。
第二年末应还款数为
280×(1+12%)
=280×1.12
=313.6(元)。
第二年末购油后,还剩欠款数
207.20÷(1+12%)
=207.20÷1.12
=185(元)。
10千克香油需要的钱数为313.6-185=128.6(元)。
所以,每千克香油价格为128.6÷10=12.86(元)。
答:每千克香油的价格是12.86元。
14
题型训练
例题精讲
11 利率、利税问题
2.国家规定个人发表文章,出版图书获得稿费的计算方法是:①稿费不高于800元的不纳税;②稿费高于800元又不高于4000元的应缴纳超过800元的那一部分的14%的税;③稿费高于4000元的应缴纳全部稿费的11%的税。今得知丁老师获得一笔稿费,并且依法缴纳个人所得税420元,问丁老师这笔稿费是多少元?又得知马老师获得一笔稿费,并且依法缴纳个人所得税550元,问马老师这笔稿费是多少元?
【答案】丁老师的稿费为3800元,马老师的稿费为5000元
【解答】第一档的不纳税,第二档的要纳税
(4000-800)×14%
=3200×14%
=448(元)
说明丁老师稿费低于4000元。
丁老师的稿费为:
420÷14%+800
=3000+800
=3800(元)。
马老师的所得税高于448元,应该用第三档的来计算。
马老师的稿费为:550÷11%=5000(元)。
答:丁老师的稿费为3800元,马老师的稿费为5000元。
14
题型训练
例题精讲
12 折扣、利润、购物方案
1.某人到商品买红、蓝两种笔,红笔定价5元,蓝笔定价9元.由于买的数量较多,商店就给打折扣.红笔按定价 85%出售,蓝笔按定价 80%出售.结果他付的钱就少了18%.已知他买了蓝笔 30支,问红笔买了几支?
【答案】36支
【解答】相当于把两种折扣的百分数配比,成为1-18%=82%.
(85%-82%)∶(82%-80%)=3∶2.
他买红、蓝两种笔的钱数之比是2∶3.
设买红笔是x支,可列出比例式
5x∶9×30=2∶3
x==36(支)
答:红笔买了 36支。
14
题型训练
例题精讲
12 折扣、利润、购物方案
2.某商店到水果产地去收购橘子,收购价为每千克1.20元。从产地到商店的距离是400千米,运费为每吨货物每运1千米收1.50元。如果在运输及销售过程中的损耗是10%,商店要想实现25%的利润率,零售价应是每千克多少元?
【答案】2.50元
【解答】每千克的运费是1.50×400÷1000=0.60(元)
每千克的成本:
(1.20+0.60)÷(1-10%)
=1.8÷0.9
=2.00(元)
零售价为:2.00×(25%+1)
=2×1.25
=2.50(元) 答:零售价应是每千克2.50元。
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(1)若小明家某月用水18立方米,则小明家该月实际应交水费多少元?
【答案】95.5元
【解答】(1)根据题意得:15×4.5+(18-15)×6+10
=15×4.5+3×6+10
=67.5+18+10
=95.5(元)。
答:小明家该月实际应交水费95.5元;
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(2)已知某户居民某月的实际应交水费为187.5元,则这户居民的该月用水量是多少立方米?
【答案】30立方米
【解答】设这户居民的该月用水量是x立方米,
∵15×4.5+(20-15)×6+10=107.5,107.5<187.5 ∴x>20
根据题意得:15×4.5+(20-15)×6+8(x-20)+10=187.5,
解得:x=30 答:这户居民的该月用水量是30立方米;
14
题型训练
例题精讲
13 分段计费
1.某城市为倡导全民节水,居民生活用水按户收费,并按阶梯计价,收费标准(户内人口不超过4人)如下表:
注:
①公摊水费:每户每月10元;
②每月实际应交水费=阶梯水费+公摊水费。
(3)若某户某月实际应交水费平均每立方米6.5元,求该户该月用水量。
【答案】5或35立方米
【解答】设该户该月用水量是y立方米,
当0<y≤15时,4.5y+10=6.5y,解得:y=5;
当15<y≤20时,15×4.5+6(y-15)+10=6.5y,解得:y=﹣25(不符合题意,舍去);
当y>20时,15×4.5+(20-15)×6+8(y-20)+10=6.5y,解得:y=35
答:该户该月用水量是5或35立方米。
14
题型训练
例题精讲
13 分段计费
2.某市出租车规定:
有一天,小红一家三人坐出租车去离家8千米远的动物园玩,动物园每张门票是58元,每人还买了一瓶1.5元的矿泉水。问小红一家共花费了多少元?
【答案】193.5元
【解答】打车费用:8+1.4×(8-3)
=8+1.4×5
=8+7
=15(元)
总费用:58×3+1.5×3+15
=174+4.5+15
=178.5+15
=193.5(元) 答:小红一家共花费了193.5元。
15
专项训练
专项练习
1.陈师傅原来每天最多能加工150个零件。自从工厂引进新设备后,陈师傅每天加工的零件个数在170~200个之间(含200个)。现在陈师傅1个月(按22天计算)最多能加工( )个零件。
2.过年了,同学们要亲手做一些工艺品送给敬老院的老人,开始时艺术小组的同学们先做一天,随后增加15位同学和他们一起又做了两天,恰好完成,假设每位同学的工作效率相同,且一位同学单独完成需要60天,那么艺术小组的同学有 ( )位。
4400
10
15
专项训练
专项练习
3.污水处理厂有600吨污水待处理,且每天新增同样多的污水需要处理,如果每天处理200吨,6天可以处理完。如果每天处理250吨,( )天可以处理完。
4.春节前夕,一个富翁向乞丐帮帮众施舍一笔钱财。一开始他准备给每人100元,结果剩下350元。他决定每人多给20元。这时从其他地方有闻讯赶来了5个乞丐,如果他们每个人拿到的钱也和其他乞丐一样多,富翁还需要再增加550元。富翁原打算施舍( )元。
4
1850
15
专项训练
专项练习
5.在一个庆典晚会上,男女嘉宾共69人。出现了一个非常有趣的情况:每位女士认识的男士的人数各不相同,而且组成连续的自然数,最少的认识16位男士,最多的只有两位男士不认识。这次晚会上,共有女嘉宾( )人。
6.假期将至,超市都在搞打折促销活动,同一品牌原价为50元的洗衣液,甲超市打七折销售,乙超市降价20%销售,丙超市“买三送一”。现在妈妈打算买4瓶洗衣液,在( )超市买更划算。
A.甲 B.乙 C.丙
26
A
15
专项训练
专项练习
7.数学竞赛共10道题,做对一题得8分,做错一题(或不做)倒扣5分,小明得41分,他共做错(或不做)了( )道题。
A.2 B.3 C.4 D.5
8.希望小学学生排成正方形方阵做早操,从前往后数小明排第7个,从后往前数排第13个,从左往右数,从右往左数都排第10个。最外层一共可以排( )个学生。
A.78 B.72 C.76 D.80
B
B
15
专项训练
专项练习
9.下列问题中,能用90-21×3解决的是( )。
①篮球每个90元,垒球每个21元,一个篮球比3个垒球贵多少元?
②工程队翻修一条90千米的路,每天修21千米,3天后还剩多少?
③篮球原价90元,现降价21元。买3个能省多少钱?
④轿车每小时行90千米,卡车每小时比它少行21千米。卡车从甲地到乙地用了3小时,甲乙两地相距多少千米?
A.①② B.③④ C.①②③ D.①②③④
10.小明调制了3杯蜂蜜水,最甜的是( )。
A.用10克蜂蜜配成110克蜂蜜水。
B.蜂蜜与水的比是1:10。
C.蜂蜜占蜂蜜水的10%。
A
C
15
专项训练
专项练习
11.李英和黄明比赛走楼梯,李英走3级楼梯时,黄明能走5级,这幢楼每两层之间有20级楼梯,那么当黄明走到6楼时,李英走到几楼?
李英、黄明的速度比=3∶5
相同时间内。速度和路程成正比
所以,李英和黄明的路程比=3∶5
当黄明走到6楼时,李英走到了:(6-1)÷5×3+1=4楼
答:当黄明走到6楼时,李英走到4楼。
15
专项训练
专项练习
12.标有A、B、C、D、E、F的6盏灯依次排成一行,每盏灯有一个开关。现在A、C、E不亮,其余3盏亮着。军军从灯A开始顺次拉动开关,即从A到F,再从A开始顺次拉动开关,他这样拉动1000次开关后,哪些灯亮着,哪些灯不亮?
1000÷6=166……4,意味着6盏灯从A到F被拉动166个循环后,A、B、C、D又被拉动各一次。因此,灯A,B,C,D各被拉动167次开关,灯E,F各被拉动166次开关。初始状态A、C、E不亮,B、D、F亮着,所以灯A,B,C,D改变了原来状态,灯E,F没改变原来状态。
故当军军拉动1000次后A,C,F亮,而B,D,E没亮。
15
专项训练
专项练习
13.欣欣、希希、望望三人分别在相距18千米的A、B两地同时动身,欣欣、希希二人从A地出发,步行去B地,望望从B地出发向,骑自行车去A地,望望首先在途中与希希相遇,10分钟后又与欣欣相遇,然后继续前进,达到A地后立马掉头返回B地,在AB的中点追上了欣欣,最后与希希同时到达B地。三人每分钟各行多少米?
18÷(1+2)×2
=18÷3×2
=6×2
=12(千米)
12÷3=4(千米)
18-12-4
=6-4
=2(千米)
=2000米
2000÷10=200(米)
200÷(1+3)
=200÷4
=50(米)
50×3=150(米)
150÷2=75(米)
答:欣欣每分钟行50米,希希每分钟行75米,望望每分钟行150米。
15
专项训练
专项练习
14.某汽车公司组织比赛,比赛规则如图所示:维修队有29人(含司机),速度为每分钟1千米(不计掉头时间),则维修队完成比赛最快需多少时间?
10÷1=10(分钟)
10×2=20(分钟)
29=4×6+5
20×6+10
=120+10
=130(分钟)
答:维修队完成比赛最快需130分钟。
15
专项训练
专项练习
15.某学校举办数学夏令营活动,由5名老师带领若干名学生参加,学校联系了两家标价相同的旅行社(每名老师和每名学生的费用也相同)。经过商议后,甲旅行社给出的优惠是:老师的费用按原价,学生的费用打七折;乙旅行社给出的优惠是:老师、学生的费用全部打八折。经过计算,甲旅行社优惠后的总费用比乙旅行社优惠后的总费用便宜10%,那么学生有多少名?
解:设学生有x名,每人100元。
500+100x×70%=100(x+5)×80%×(1-10%)
500+70x=80(x+5)×90%
500+70x=72(x+5)
500+70x=72x+360
72x-70x=500-360
2x=140
x=140÷2
x=70
答:学生有70名。
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
