苏科版数学九年级上第1单元一元二次方程单元测试卷(含答案)
文档属性
| 名称 | 苏科版数学九年级上第1单元一元二次方程单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 56.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-03 07:59:49 | ||
图片预览



文档简介
2015-2016学年南京市扬子一中
九年级上数学一元二次方程单元测试卷
班级 姓名
一、选择题
1.若(m+1)xm(m+2﹣1)+2mx﹣1=0是关于x的一元二次方程,则m的值是 .
2.若a+b+c=0,且a≠0,则一元二次方程ax2+bx+c=0必有一个定根,它是 .
3. 2013年国家扶贫开发工作重点县农村 ( http: / / www.21cnjy.com )居民人均纯收入为2027元,2015年增长到3985元.若设年平均增长率为x,则根据题意可列方程为 .
4.如果--8=0,则的值是________.
5.关于x的方程(m2-1)x2+(m-1)x+2m-1=0是一元二次方程的条件是________.
6.关于x的一元二次方程x2-x-3m=0有两个不相等的实数根,则m的取值范围是定______________.
7.x2-5│x│+4=0的所有实数根的和是________.
8.方程x4-5x2+6=0,设y=x2,则原方程变形为___________________,原方程的根为________.
9、以-3和7为根且二次项系数为1的一元二次方程是 。
10、关于的一元二次方程有一个根为零,那的值等于 。
二、选择题
11.用配方法解方程,下列配方正确的是( )
A. B. C. D.
12.已知一元二次方程,下列判断的是( )
A.该方程有两个相等的实数根 B.该方程有两不个相等的实数根
C.该方程无实数根 D.该方程根的情况不确定
13.使分式的值等于零的的值是( )
A.6 B.或6 C. D.
14.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )
A、 B、 C、 D、
15.已知α,β是方程x2+2006x+1=0的两个根,则(1+2008α+α2)(1+2008β+β2)的值为( ).
A.1 B.2 C.3 D.4
16.三角形两边长分别为2和4,第三边是方程x2-6x+8=0的解,则这个三角形的周长是( ).
A.8 B.8或10 C.10 D.8和10
三、用适当的方法解方程
17.(1)2(x+2)2-8=0; (2)x(x-3)=x;
(3)x2=6x-; (4)(x+3)2+3(x+3)-4=0.
四、解答题
18.如果x2-10x+y2-16y+89=0,求的值.
19.阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用___________法达到________的目的,体现了数学的转化思想.
(2)解方程(x2+x)2-4(x2+x)-12=0.
20.山西特产专卖店销售核桃,其进价为每千 ( http: / / www.21cnjy.com )克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
21.一个广告公司制作广告 ( http: / / www.21cnjy.com )的收费标准是:以面积为单位,在不超过规定面积A(m2)的范围内,每张广告收费1 000元,若超过Am2,则除了要交这1 000元的基本广告费以外,超过部分还要按每平方米50A元缴费.下表是该公司对两家用户广告的面积及相应收费情况的记载:
单位 广告的面积(m2) 收费金额(元)
烟草公司 6 1400
食品公司 3 1000
红星公司要制作一张大型公益广告,其材料 ( http: / / www.21cnjy.com )形状是矩形,它的四周是空白,如果上、下各空0.25m,左、右各空0.5m,那么空白部分的面积为6m2.已知矩形材料的长比宽多1m,并且空白部分不收广告费,那么这张广告的费用是多少?
22.设a,b,c是△ABC的三条边,关于x的方程x2+ HYPERLINK "http://" x+c-a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状.
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
23.已知关于x的方程a2x2+( ( http: / / www.21cnjy.com )2a-1)x+1=0有两个不相等的实数根x1,x2.(1)求a的取值范围;(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得△=(2a-1)2-4a2>0,解得a<.
∴当a<0时,方程有两个不相等的实数根.
(2)存在,如果方程的两个实数根x1,x2互为相反数,则x1+x2=-(2a—1)/a.a=0 ①,
解得a=,经检验,a=是方程①的根.
∴当a=时,方程的两个实数根x1与x2互为相反数.
上述解答过程是否有错误?如果有,请指出错误之处,并解答.
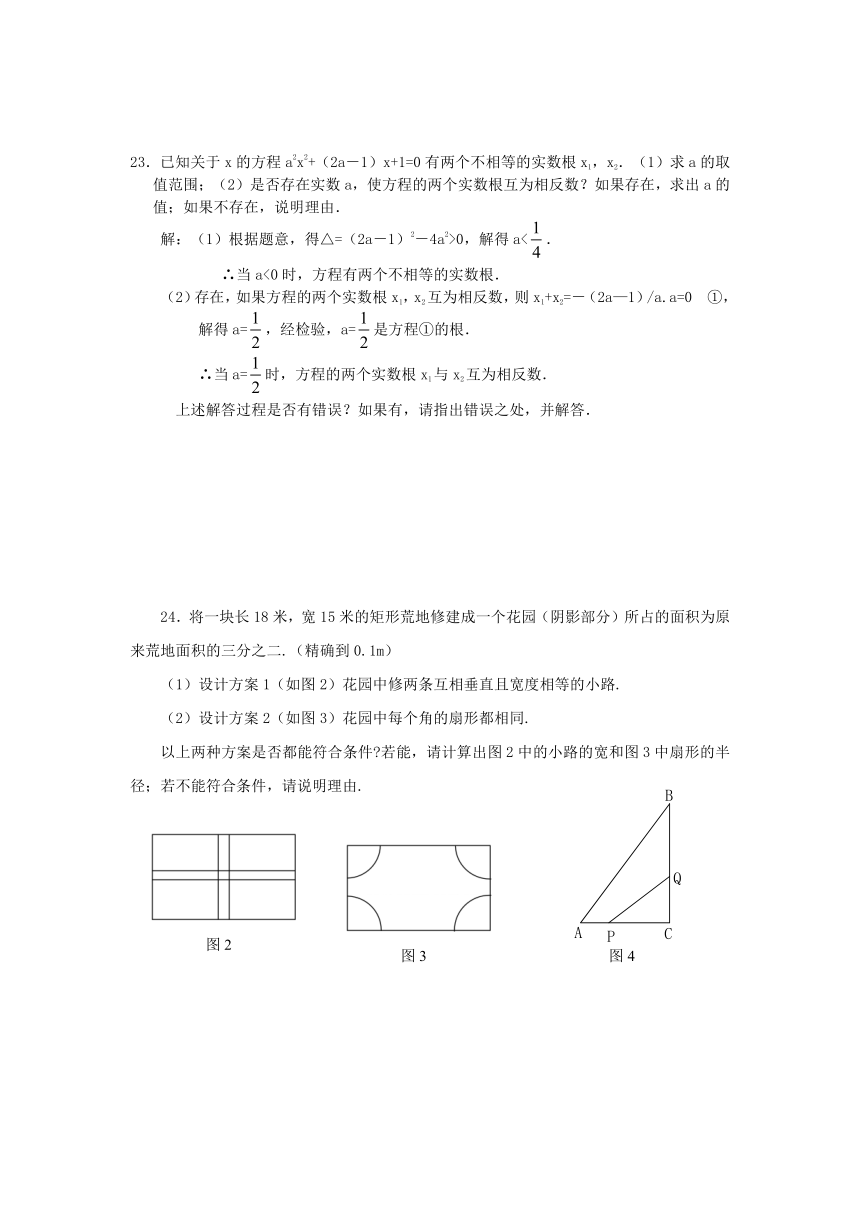
24.将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图2)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图3)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件 若能,请计算出图2中的小路的宽和图3中扇形的半径;若不能符合条件,请说明理由.
25.如图4所示,在△ABC中,∠ ( http: / / www.21cnjy.com )C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
26.如图5所示,我海军基地位于A处,在其正 ( http: / / www.21cnjy.com )南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D恰好位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航.一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送往军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(精确到0.1海里)
参考答案:
一、填空题
1.m=1或m=﹣2
2.1
3.2027(1+x)2=3985.
4.4 -2 点拨:把看做一个整体.
5.m≠±1
6.m>- 点拨:理解定义是关键.
7.0 点拨:绝对值方程的解法要掌握分类讨论的思想.
8.y2-5y+6=0 x1=,x2=-,x3=,x4=-
9. x-4x-21=0
10. -3
二、选择题
11.A 12.B 13.A
14.C 15.D 16.C
三、用适当的方法解方程
17.(1)整理得(x+2)2=4,
即(x+2)=±2,
∴x1=0,x2=-4
(2)x(x-3)-x=0,
x(x-3-1)=0,
x(x-4)=0,
∴x1=0,x2=4.
(3)整理得x2+-6x=0,
x2-2x+1=0,
由求根公式得x1=+,x2= HYPERLINK "http://" -.
(4)设x+3=y,原式可变为y2+3y-4=0,
解得y1=-4,y2=1,
即x+3=-4,x=-7.
由x+3=1,得x=-2.
∴原方程的解为x1=-7,x2=-2.
四、解答题
18.由已知x2-10x+y2-16y+89=0,
得(x-5)2+(y-8)2=0,
∴x=5,y=8,∴=.
19.(1)换元 降次
(2)设x2+x=y,原方程可化为y2-4y-12=0,
解得y1=6,y2=-2.
由x2+x=6,得x1=-3,x2=2.
由x2+x=-2,得方程x2+x+2=0,
b2-4ac=1-4×2=-7<0,此时方程无解.
所以原方程的解为x1=-3,x2=2.
20.(1)解:设每千克核桃应降价x元.
根据题意,得 (60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),.
答:该店应按原售价的九折出售. …10分
21.解:由表可知,3≤A<6,根据题意,得1000+50A(6﹣A)=1400,
解得A1=4,A2=2(舍去),
∴A=4.
设矩形材料的宽为xm,长为(x+1)m,
由题意,得2×0.25(x+1)+2×0.5(x﹣0.25×2)=6,
解得x=4.
所以矩形材料的长为5m,宽为4m,
广告部分的面积为5×4﹣6=14m2,
广告的费用为1000+50×4×(14﹣4)=1000+2000=3000(元).
答:这张广告的费用是3000元.
22.∵x2+x+c-a=0有两个相等的实数根,
∴判别式=()2-4×(c-a)=0,
整理得a+b-2c=0 ①,
又∵3cx+2b=2a的根为x=0,
∴a=b ②.
把②代入①得a=c,
∴a=b=c,∴△ABC为等边三角形.
(2)a,b是方程x2+mx-3m=0的两个根,
所以m2-4×(-3m)=0,即m2+12m=0,
∴m1=0,m2=-12.
当m=0时,原方程的解为x=0(不符合题意,舍去),
∴m=12.
23.上述解答有错误.
(1)若方程有两个不相等实数根,则方程首先满足是一元二次方程,
∴a2≠0且满足(2a-1)2-4a2>0,∴a<且a≠0.
(2)a不可能等于.
∵(1)中求得方程有两个不相等实数根,同时a的取值范围是a<且a≠0,
而a=>(不符合题意)
所以不存在这样的a值,使方程的两个实数根互为相反数.
24.解 都能.(1)设小路宽为x,则18x+16x-x2=×18×15,即x2-34x+180=0,
解这个方程,得x= HYPERLINK "http://" ,即x≈6.6.
(2)设扇形半径为r,则3.14r2=×18×15,即r2≈57.32,所以r≈7.6.
25.解 因为∠C=90°,所以AB===10(cm).
(1)设xs后,可使△PCQ的面积为8cm2,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.
则根据题意,得·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,
得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.
则根据题意,得(6-x)·2x=××6×8.整理,得x2-6x+12=0.
由于此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.
26.解(1)F位于D的正南方向,则DF⊥BC.因为AB⊥BC,D为AC的中点,所以DF=AB=100海里,所以,小岛D与小岛F相距100海里.
(2)设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,EF=AB+BC-(AB+BE)-CF=(300-2x)海里.
在Rt△DEF中,根据勾股定理可得方程x2=1002+(300-2x)2,
整理,得3x2-1200x+100000=0.
解这个方程,得x1=200-≈118.4,x2=200+(不合题意,舍去).所以,相遇时补给船大约航行了118.4海里.
图2
图4
图3
图5
九年级上数学一元二次方程单元测试卷
班级 姓名
一、选择题
1.若(m+1)xm(m+2﹣1)+2mx﹣1=0是关于x的一元二次方程,则m的值是 .
2.若a+b+c=0,且a≠0,则一元二次方程ax2+bx+c=0必有一个定根,它是 .
3. 2013年国家扶贫开发工作重点县农村 ( http: / / www.21cnjy.com )居民人均纯收入为2027元,2015年增长到3985元.若设年平均增长率为x,则根据题意可列方程为 .
4.如果--8=0,则的值是________.
5.关于x的方程(m2-1)x2+(m-1)x+2m-1=0是一元二次方程的条件是________.
6.关于x的一元二次方程x2-x-3m=0有两个不相等的实数根,则m的取值范围是定______________.
7.x2-5│x│+4=0的所有实数根的和是________.
8.方程x4-5x2+6=0,设y=x2,则原方程变形为___________________,原方程的根为________.
9、以-3和7为根且二次项系数为1的一元二次方程是 。
10、关于的一元二次方程有一个根为零,那的值等于 。
二、选择题
11.用配方法解方程,下列配方正确的是( )
A. B. C. D.
12.已知一元二次方程,下列判断的是( )
A.该方程有两个相等的实数根 B.该方程有两不个相等的实数根
C.该方程无实数根 D.该方程根的情况不确定
13.使分式的值等于零的的值是( )
A.6 B.或6 C. D.
14.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )
A、 B、 C、 D、
15.已知α,β是方程x2+2006x+1=0的两个根,则(1+2008α+α2)(1+2008β+β2)的值为( ).
A.1 B.2 C.3 D.4
16.三角形两边长分别为2和4,第三边是方程x2-6x+8=0的解,则这个三角形的周长是( ).
A.8 B.8或10 C.10 D.8和10
三、用适当的方法解方程
17.(1)2(x+2)2-8=0; (2)x(x-3)=x;
(3)x2=6x-; (4)(x+3)2+3(x+3)-4=0.
四、解答题
18.如果x2-10x+y2-16y+89=0,求的值.
19.阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用___________法达到________的目的,体现了数学的转化思想.
(2)解方程(x2+x)2-4(x2+x)-12=0.
20.山西特产专卖店销售核桃,其进价为每千 ( http: / / www.21cnjy.com )克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
21.一个广告公司制作广告 ( http: / / www.21cnjy.com )的收费标准是:以面积为单位,在不超过规定面积A(m2)的范围内,每张广告收费1 000元,若超过Am2,则除了要交这1 000元的基本广告费以外,超过部分还要按每平方米50A元缴费.下表是该公司对两家用户广告的面积及相应收费情况的记载:
单位 广告的面积(m2) 收费金额(元)
烟草公司 6 1400
食品公司 3 1000
红星公司要制作一张大型公益广告,其材料 ( http: / / www.21cnjy.com )形状是矩形,它的四周是空白,如果上、下各空0.25m,左、右各空0.5m,那么空白部分的面积为6m2.已知矩形材料的长比宽多1m,并且空白部分不收广告费,那么这张广告的费用是多少?
22.设a,b,c是△ABC的三条边,关于x的方程x2+ HYPERLINK "http://" x+c-a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状.
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
23.已知关于x的方程a2x2+( ( http: / / www.21cnjy.com )2a-1)x+1=0有两个不相等的实数根x1,x2.(1)求a的取值范围;(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得△=(2a-1)2-4a2>0,解得a<.
∴当a<0时,方程有两个不相等的实数根.
(2)存在,如果方程的两个实数根x1,x2互为相反数,则x1+x2=-(2a—1)/a.a=0 ①,
解得a=,经检验,a=是方程①的根.
∴当a=时,方程的两个实数根x1与x2互为相反数.
上述解答过程是否有错误?如果有,请指出错误之处,并解答.
24.将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图2)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图3)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件 若能,请计算出图2中的小路的宽和图3中扇形的半径;若不能符合条件,请说明理由.
25.如图4所示,在△ABC中,∠ ( http: / / www.21cnjy.com )C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
26.如图5所示,我海军基地位于A处,在其正 ( http: / / www.21cnjy.com )南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D恰好位于AC的中点,岛上有一补给码头;小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航.一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送往军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(精确到0.1海里)
参考答案:
一、填空题
1.m=1或m=﹣2
2.1
3.2027(1+x)2=3985.
4.4 -2 点拨:把看做一个整体.
5.m≠±1
6.m>- 点拨:理解定义是关键.
7.0 点拨:绝对值方程的解法要掌握分类讨论的思想.
8.y2-5y+6=0 x1=,x2=-,x3=,x4=-
9. x-4x-21=0
10. -3
二、选择题
11.A 12.B 13.A
14.C 15.D 16.C
三、用适当的方法解方程
17.(1)整理得(x+2)2=4,
即(x+2)=±2,
∴x1=0,x2=-4
(2)x(x-3)-x=0,
x(x-3-1)=0,
x(x-4)=0,
∴x1=0,x2=4.
(3)整理得x2+-6x=0,
x2-2x+1=0,
由求根公式得x1=+,x2= HYPERLINK "http://" -.
(4)设x+3=y,原式可变为y2+3y-4=0,
解得y1=-4,y2=1,
即x+3=-4,x=-7.
由x+3=1,得x=-2.
∴原方程的解为x1=-7,x2=-2.
四、解答题
18.由已知x2-10x+y2-16y+89=0,
得(x-5)2+(y-8)2=0,
∴x=5,y=8,∴=.
19.(1)换元 降次
(2)设x2+x=y,原方程可化为y2-4y-12=0,
解得y1=6,y2=-2.
由x2+x=6,得x1=-3,x2=2.
由x2+x=-2,得方程x2+x+2=0,
b2-4ac=1-4×2=-7<0,此时方程无解.
所以原方程的解为x1=-3,x2=2.
20.(1)解:设每千克核桃应降价x元.
根据题意,得 (60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),.
答:该店应按原售价的九折出售. …10分
21.解:由表可知,3≤A<6,根据题意,得1000+50A(6﹣A)=1400,
解得A1=4,A2=2(舍去),
∴A=4.
设矩形材料的宽为xm,长为(x+1)m,
由题意,得2×0.25(x+1)+2×0.5(x﹣0.25×2)=6,
解得x=4.
所以矩形材料的长为5m,宽为4m,
广告部分的面积为5×4﹣6=14m2,
广告的费用为1000+50×4×(14﹣4)=1000+2000=3000(元).
答:这张广告的费用是3000元.
22.∵x2+x+c-a=0有两个相等的实数根,
∴判别式=()2-4×(c-a)=0,
整理得a+b-2c=0 ①,
又∵3cx+2b=2a的根为x=0,
∴a=b ②.
把②代入①得a=c,
∴a=b=c,∴△ABC为等边三角形.
(2)a,b是方程x2+mx-3m=0的两个根,
所以m2-4×(-3m)=0,即m2+12m=0,
∴m1=0,m2=-12.
当m=0时,原方程的解为x=0(不符合题意,舍去),
∴m=12.
23.上述解答有错误.
(1)若方程有两个不相等实数根,则方程首先满足是一元二次方程,
∴a2≠0且满足(2a-1)2-4a2>0,∴a<且a≠0.
(2)a不可能等于.
∵(1)中求得方程有两个不相等实数根,同时a的取值范围是a<且a≠0,
而a=>(不符合题意)
所以不存在这样的a值,使方程的两个实数根互为相反数.
24.解 都能.(1)设小路宽为x,则18x+16x-x2=×18×15,即x2-34x+180=0,
解这个方程,得x= HYPERLINK "http://" ,即x≈6.6.
(2)设扇形半径为r,则3.14r2=×18×15,即r2≈57.32,所以r≈7.6.
25.解 因为∠C=90°,所以AB===10(cm).
(1)设xs后,可使△PCQ的面积为8cm2,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.
则根据题意,得·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,
得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.
则根据题意,得(6-x)·2x=××6×8.整理,得x2-6x+12=0.
由于此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.
26.解(1)F位于D的正南方向,则DF⊥BC.因为AB⊥BC,D为AC的中点,所以DF=AB=100海里,所以,小岛D与小岛F相距100海里.
(2)设相遇时补给船航行了x海里,那么DE=x海里,AB+BE=2x海里,EF=AB+BC-(AB+BE)-CF=(300-2x)海里.
在Rt△DEF中,根据勾股定理可得方程x2=1002+(300-2x)2,
整理,得3x2-1200x+100000=0.
解这个方程,得x1=200-≈118.4,x2=200+(不合题意,舍去).所以,相遇时补给船大约航行了118.4海里.
图2
图4
图3
图5
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
