第1-5单元必考题检测卷(含答案)2024-2025学年数学五年级下册苏教版
文档属性
| 名称 | 第1-5单元必考题检测卷(含答案)2024-2025学年数学五年级下册苏教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 521.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 13:31:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-5单元必考题检测卷-2024-2025学年数学五年级下册苏教版
一、选择题
1.等式与方程的关系可以用如图中的( )来表示。
A. B.
C. D.
2.甲、乙两筐苹果,甲筐64千克,乙筐千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程错误的是( )。
A. B. C. D.
3.妈妈从水果店买回了同样多的一家人每天吃4个苹果和3个梨。过了几天,苹果刚好吃完,梨还剩8个。已经吃了( )天。
A.4 B.6 C.8 D.10
4.李师傅和王师傅一起修剪一块草坪,两人修剪草坪的速度相同。一开始两人同时修剪,修剪一段时间后,李师傅有事离开,只留下王师傅一人修剪。在下面四幅图中,图( )能表示修剪时间t和修剪面积S之间的关系。
A. B.
C. D.
5.有两个不是0的自然数,它们之间的关系为,这两个数的最小公倍数是( )。
A. B. C.0.5 D.4
6.把7克糖溶解在100克水中,水占糖水的( )。
A. B. C. D.
7.,变形的依据是( )。
A.加法交换律 B.加法结合律 C.加法交换律和加法结合律 D.以上都不对
8.甲、乙两根绳子同样长,甲绳用去米,乙绳用去后,剩下的绳子相比,( )。
A.甲绳长 B.乙绳长 C.同样长 D.无法确定哪根长
二、填空题
9.,这样计算的依据是( )。
10.某班有的学生喜欢跳绳,的学生喜欢踢毽子,其他学生喜欢球类运动。这个班喜欢球类运动的学生占( )。
11.看图填空。
(1)
( )个番茄和一个萝卜同样重。
(2)
一个苹果和( )个草莓同样重。
12.快、慢两辆汽车分别从甲、乙两地同时相对开出,2小时后在距离中点20千米的地方相遇,快车每小时行驶80千米,慢车的速度是( )千米/时。
13.从0、3、4、5四个数字中任选三个组成三位数,其中能同时被2、3整除的有( )个,能同时被2、3、5整除的有( )。
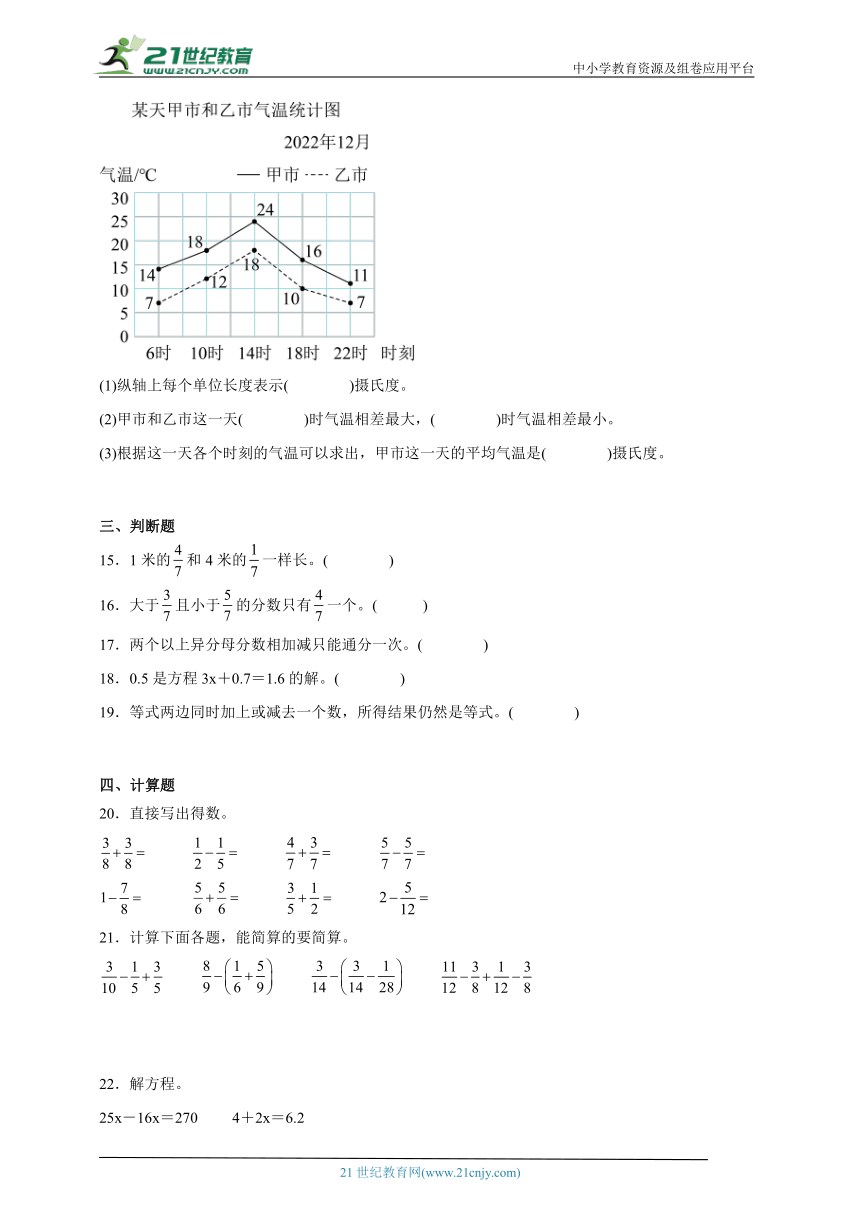
14.看图回答问题。
(1)纵轴上每个单位长度表示( )摄氏度。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )摄氏度。
三、判断题
15.1米的和4米的一样长。( )
16.大于且小于的分数只有一个。( )
17.两个以上异分母分数相加减只能通分一次。( )
18.0.5是方程3x+0.7=1.6的解。( )
19.等式两边同时加上或减去一个数,所得结果仍然是等式。( )
四、计算题
20.直接写出得数。
21.计算下面各题,能简算的要简算。
22.解方程。
25x-16x=270 4+2x=6.2
1.8x÷3=2.4 3×0.9+4x=22.7
五、解答题
23.公路一边共有水杉树52棵,原来每相邻两棵树之间的距离都是8米,现在因树长大了显得较密,要把每相邻两棵树之间的距离改成12米。如果起点的树不移动,那么不需要移动的树还有多少棵?
24.4年前姐姐的年龄是弟弟的2倍,今年姐姐12岁。今年弟弟几岁?(只列方程,不解答)
25.甲、乙两人沿着400米长的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是200米/分,乙的速度是160米/分。经过多少分钟甲第二次追上乙?
26.敏敏参加60米短跑训练,第一周训练时平均每次用时分钟,第二周训练时平均每次用时分钟。第二周比第一周的训练成绩是提高了还是退步了?
27.五(1)班乒乓球组的人数占全班人数的,美术组的人数占全班人数的,没有人同时参加乒乓球组和美术组。
(1)美术组和乒乓球组的人数共占全班人数的几分之几?
(2)乒乓球组的人数比美术组的人数多占全班人数的几分之几?
28.小明选了些饱满的蒜瓣种在两个盆里,分别标注1号盆和2号盆。1号盆放在室外,2号盆放在室内。从第6天开始,每两天一次,测量两盆蒜瓣中长出的最长叶片长,进行记录。下表是前16天记录的数据,请根据记录情况完成问题。
蒜叶生长情况记录表
第6天 第8天 第10天 第12天 第14天 第16天
1号盆最长叶片长/毫米 8 21 42 55 75 100
2号盆最长叶片长/毫米 5 10 22 30 45 60
(1)根据记录的数据完成统计图。
(2)在室外和室内,蒜叶生长变化情况有什么相同点和不同点?
(3)你还能从数据中获得哪些信息?
《第1-5单元必考题检测卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B C C B C C D
1.C
【分析】含有等号的式子叫做等式。含有未知数的等式叫做方程。
方程一定是等式,等式不一定是方程。所以等式包含方程。
【详解】等式与方程的关系可以用下图表示:
故答案为:C
2.B
【分析】用方程解决问题的关键是找到等量关系。从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多(4+4)千克,设乙筐千克,根据甲筐质量-乙筐质量=甲筐比乙筐多的质量,乙筐质量+甲筐比乙筐多的质量=甲筐质量,乙筐质量+甲筐放入乙筐的质量=甲筐质量-甲筐放入乙筐的质量,可以列出方程。
【详解】A.,等量关系:甲筐质量-乙筐质量=甲筐比乙筐多的质量,方程正确;
B.,等量关系:乙筐质量+甲筐放入乙筐的质量≠甲筐质量,方程错误;
C.,等量关系:乙筐质量+甲筐比乙筐多的质量=甲筐质量,方程正确;
D.,等量关系:乙筐质量+甲筐放入乙筐的质量=甲筐质量-甲筐放入乙筐的质量,方程正确。
方程错误的是。
故答案为:B
3.C
【分析】由题意可知,苹果和梨一样多,一家人每天吃4个苹果和3个梨。过了几天,苹果刚好吃完,梨还剩8个。设已经吃了x天,根据苹果吃掉的总数-吃掉梨的总数=8个,列方程计算即可得解。
【详解】解:设已经吃了x天。
4x-3x=8
解得x=8
已经吃了8天。
故答案为:C
4.C
【分析】分析题目,开始时李师傅和王师傅两人一起修剪,根据修剪总面积=单位时间的修剪面积×修剪时间可知,S随着t的增长而增长较快,即直线比较陡峭;后面李师傅离开后,只剩下王师傅一个人修剪,此时S随着t的增长而增长的较慢,即直线比较平缓,据此解答即可。
【详解】
根据分析可知,能表示修剪时间t和修剪面积S之间的关系。
故答案为:C
5.B
【分析】由a÷0.5=b,可得a=0.5b,也就是b=2a,说明b是a的整数倍;求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数为较大的数;由此解答问题即可。
【详解】由a÷0.5=b,可得a=0.5b,则,b=2a,
也就是a和b成倍数关系,a和b的最小公倍数为b。
即,有两个不是0的自然数,它们之间的关系为a÷0.5=b,这两个数的最小公倍数是b。
故答案为:B
6.C
【分析】,要先求出糖水的质量,再根据求一个数是另一个数的几分之几用除法计算,求出水占糖水的几分之几。
【详解】7+100=107(克)
100÷107=
所以水占糖水的。
故答案为:C
7.C
【分析】观察算式,发现有2个分母为12的分数,可以把它们先加,这样计算更简便;根据加法交换律a+b=b+a、加法结合律(a+b)+c=a+(b+c)把算式变成进行简算。
【详解】
所以,,变形的依据是加法交换律和加法结合律。
故答案为:C
8.D
【分析】分别将两根绳子的长度看作单位“1”,因为绳子长度不确定,无法确定乙绳用去的长度,也无法确定两根绳子剩下的长度,因此无法进行比较,举例说明即可。
举例求剩下绳子长度的方法:甲绳:绳子长度-甲绳用的长度=甲绳剩下的长度;乙绳:根据分数的意义,分母表示平均分的份数,分子表示取走的份数,绳子长度÷分母×分子=用去的长度,绳子长度-乙绳用的长度=乙绳剩下的长度。
【详解】假设两根绳子都是1米。
1米的是米,1-=(米)
如果两根绳子都是1米,则剩下的绳子相比,同样长。
假设两根绳子都是2米。
甲:2-=(米)
乙:2÷2×1=1(米)
2-1=1(米)
>1,如果两根绳子都是2米,剩下的绳子相比,甲绳长。
假设两根绳子都是0.8米。
甲:0.8-=0.8-0.5=0.3(米)
乙:0.8÷2×1=0.4(米)
0.8-0.4=0.4(米)
0.3<0.4,如果两根绳子都是0.8米,剩下的绳子相比,乙绳长。
因此无法确定哪根长。
故答案为:D
9.减法的性质
【分析】计算时,可以根据减法的性质a-b-c=a-(b+c)把算式变成进行简算。
【详解】,这样计算的依据是(减法的性质)。
10.
【分析】把全班学生的人数看作单位“1”,根据减法的意义,用“1”减去喜欢跳绳、喜欢踢毽子的学生占全班人数分率之和,即是这个班喜欢球类运动的学生占全班人数的几分之几。
【详解】1-(+)
=1-(+)
=1-
=
这个班喜欢球类运动的学生占。
11.(1)3
(2)8
【分析】(1)从图中可知,两个萝卜的重量=一个萝卜和三个番茄的重量,根据等式的性质1将等式的两边同时减去一个萝卜,等式仍然成立。
(2)一个苹果和2个草莓的质量=10个草莓的质量,则将等式的两边同时减两个草莓等式仍然成立。
【详解】(1)1个萝卜的重量+1个萝卜-1个萝卜=一个萝卜+三个番茄-1个萝卜
则3个番茄和一个萝卜同样重。
(2)一个苹果+2个草莓的质量-2个草莓=10个草莓的质量-2个草莓
一个苹果和8个草莓同样重。
12.60
【分析】因为2小时后在距离中点20千米的地方相遇,这意味着快车超过中点20千米,而慢车距离中点还有20千米。所以在这2小时内,快车比慢车多行驶的路程就是这两个20千米,即20×2=40千米;设慢车的速度是x千米/小时,根据速度差×时间=路程差列方程解答即可。
【详解】解:设慢车的速度是x千米/小时。
(80-x)×2=20×2
(80-x)×2=40
(80-x)×2÷2=40÷2
80-x=20
80-x+x=20+x
20+x=80
20+x-20=80-20
x=60
所以慢车的速度是60千米/小时。
13. 5 540、450
【分析】能被2整除的数:个位数是0、2、4、6、8,即偶数。
能被3整除的数:各位数字之和能被3整除。
能被5整除的数:个位数是0或5。
则同时被2和3整除的三位数:个位是偶数(0或4),且各位数字之和能被3整除。
同时被2、3、5整除的三位数:个位为0,且各位数字之和能被3整除。
【详解】同时被2和3整除的三位数
组合分析:组合0、3、4:无符合条件的三位数。
组合0、3、5:无符合条件的三位数。
组合0、4、5:可组成450(和9)、540(和9)、504(和9),共3个。
组合3、4、5:可组成354(和12)、534(和12),共2个。
则其中能同时被2、3整除的有5个;
同时被2、3、5整除的三位数
组合分析:组合0、4、5:可组成450(和9)、540(和9),共2个。
能同时被2、3、5整除的有450、540;
14.(1)5
(2) 6 22
(3)16.6
【分析】(1)纵轴表示气温,观察纵轴即可确定每个单位长度表示的温度;
(2)分别计算每个时刻的气温差,比较即可;
(3)根据平均数=总数量÷总份数,列式计算即可。
【详解】(1)纵轴上每个单位长度表示5摄氏度。
(2)14-7=7(摄氏度)、18-12=6(摄氏度)、24-18=6(摄氏度)、
16-10=6(摄氏度)、11-7=4(摄氏度)
7>6>4
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(摄氏度)
甲市这一天的平均气温是16.6摄氏度。
15.√
【分析】1米的,表示把1米看作单位“1”,平均分成7份,取其中的4份,即是米;
4米的,表示把4米看作单位“1”,平均分成7份,取其中的1份,即是米;
据此判断。
【详解】1米的和4米的都表示米,所以1米的和4米的一样长。
原题说法正确。
故答案为:√
16.×
【分析】大于而小于的同分母分数有;如果根据分数的基本性质,、的分子、分母都乘2就是、,大于而小于的分数有、、3个分数;、的分子分母都乘3就是、,大于而小于的分数有、、、、5个分数;、的分子、分母都乘4、5、6它们之间的分数有无数个。
【详解】据分析可知,大于且小于的分数有无数个。原题说法错误。
故答案为:×
17.×
【分析】把异分母分数化成和原来分数相等的同分母分数,叫做通分。
异分母分数的加减法,先通分,然后按照同分母分数的加减法进行计算。多个异分母分数相加减时,可以一次通分,也可以多次分步通分。
【详解】如:-+
=-+
=+
=+
=
通分了两次。
所以,两个以上异分母分数相加减可以多次分步通分,也可以一次通分。
原题说法错误。
故答案为:×
18.×
【分析】分析题目,先根据等式的基本性质求出3x+0.7=1.6的解,再判断即可。
【详解】3x+0.7=1.6
解:3x+0.7-0.7=1.6-0.7
3x=0.9
3x÷3=0.9÷3
x=0.3
所以,x=0.3是方程3x+0.7=1.6的解;原说法错误。
故答案为:×
19.×
【分析】根据等式的基本性质,等式两边同时加上或减去同一个数,左右两边仍然相等。
【详解】题目中“一个数”没有说明是同一个数,如1+3=4;1+3-2≠4-1;所以等式两边同时加上或减去一个相同的数,所得结果才是等式。原题干说法错误。
故答案为:×
20.;;1;0;
;;;
【详解】略
21.;;;
【分析】(1)先把三个分数通分成分母是10的分数,再从左往右依次计算;
(2)根据减法的性质,把原式改写为简算;
(3)根据“去括号”的方法,把原式改写为简算;
(4)运用“带着符号搬家”的方法和减法的性质,把原式改写为简算。
【详解】
=
=0+
=
22.x=30;x=1.1
x=4;x=5
【分析】(1)仔细观察方程及数据特点可知,先计算25x减去16x的结果。25x-16x=9x,然后在方程两边同时除以9即可解方程。
(2)仔细观察方程及数据特点可知,方程两边同时减去4先算出2x的值,然后在方程两边同时除以2即可解方程。
(3)仔细观察方程及数据特点可知,方程两边同时乘3先算出1.8x的值,然后在方程两边同时除以1.8即可解方程。
(4)仔细观察方程及数据特点可知,先计算出3乘0.9的结果。3×0.9=2.7,方程两边同时减去2.7算出4x的值,然后在方程两边同时除以4即可解方程。
【详解】25x-16x=270
解:9x=270
9x÷9=270÷9
x=30
4+2x=6.2
解:4+2x-4=6.2-4
2x=2.2
2x÷2=2.2÷2
x=1.1
1.8x÷3=2.4
解:1.8x÷3×3=2.4×3
1.8x=7.2
1.8x÷1.8=7.2÷1.8
x=4
3×0.9+4x=22.7
解:2.7+4x=22.7
2.7+4x-2.7=22.7-2.7
4x=20
4x÷4=20÷4
x=5
23.17棵
【分析】分析题目,先根据52棵树之间有(52-1)个间隔,用间隔数乘8求出公路的总长度,再求出8和12的最小公倍数是24,即每隔24米的长度对应的树是不需要移动的,据此用公路的总长度除以24即可解答。
【详解】(52-1)×8
=51×8
=408(米)
8和12的最小公倍数是24,
408÷24=17(棵)
答:不需要移动的树有17棵。
24.解:设今年弟弟x岁。
2(x-4)=12-4
【分析】求一个数的几倍是多少用乘法,设今年弟弟x岁,根据(今年弟弟的年龄-4)×2=今年姐姐的年龄-4,列出方程即可。
【详解】解:设今年弟弟x岁。
2(x-4)=12-4
2x-8=8
2x-8+8=8+8
2x=16
2x÷2=16÷2
x=8
答:今年弟弟8岁。
25.20分钟
【分析】甲、乙两人沿着环形跑道跑步,他们同时从一地点出发,同向而行,甲第一次追上乙,需要比乙一共多跑整整一圈400米;第二次追上乙要多跑整整两圈,即400×2=800米。也就是两人的路程差相差800米,设经过x分钟甲第二次追上乙;根据路程=速度×时间;用甲每分钟的速度×x分钟,求出甲x分钟跑的路程;用乙每分钟跑的路程×x,求出乙x分钟跑的路程,再用甲跑的路程-乙跑的路程=两人路程差,列方程:200x-160x=400×2,解方程,即可解答。
【详解】解:设经过x分钟甲第二次追上乙。
200x-160x=400×2
200x-160x=800
40x=800
40x÷40=800÷40
x=20
答:经过20分钟甲第二次追上乙。
【点睛】理解在环形跑道追及问题中,若两人同时同向出发,快着第几次追上慢者,就需要比慢者多跑几个全程是解答本题的关键。
26.退步了
【分析】根据题意,比较两周训练时平均每次所用的时间即可,所用时间越短,成绩越好。
异分母分数比较大小,先通分成分母相同的分数,再按照同分母分数的比较方法比较大小。据此解答。
【详解】=
=
<,则<。
答:第二周比第一周的训练成绩退步了。
27.(1)
(2)
【分析】(1)用加法求出乒乓球组、美术组的人数占全班人数的分率之和,即是美术组和乒乓球组的人数共占全班人数的几分之几。
(2)用乒乓球组的人数占全班人数的分率减去美术组的人数占全班人数的分率,即是乒乓球组的人数比美术组的人数多占全班人数的几分之几。
【详解】(1)
答:美术组和乒乓球组的人数共占全班人数的。
(2)
答:乒乓球组的人数比美术组的人数多占全班人数的。
28.(1)见详解
(2)相同点:蒜叶中的最长叶片的长度都在逐渐变长;不同点:在室外生长的蒜叶长得快一些
(3)第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米
【分析】(1)根据统计表中的数据将折线统计图补充完整即可。
(2)由统计图可知,表示两个盆蒜叶生长情况的折线一直在上升,说明两个盆中的蒜叶一直在生长;而1号盆对应的折线更陡一些,说明1号盆蒜叶生长快一些,2号盆蒜叶生长慢一些。
(3)根据统计表和统计图获取相关的数学信息即可。如:第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米
【详解】
(1)
(2)答:相同点:蒜叶中的最长叶片的长度都在逐渐变长;不同点:在室外生长的蒜叶长得快一些。
(3)答:第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-5单元必考题检测卷-2024-2025学年数学五年级下册苏教版
一、选择题
1.等式与方程的关系可以用如图中的( )来表示。
A. B.
C. D.
2.甲、乙两筐苹果,甲筐64千克,乙筐千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程错误的是( )。
A. B. C. D.
3.妈妈从水果店买回了同样多的一家人每天吃4个苹果和3个梨。过了几天,苹果刚好吃完,梨还剩8个。已经吃了( )天。
A.4 B.6 C.8 D.10
4.李师傅和王师傅一起修剪一块草坪,两人修剪草坪的速度相同。一开始两人同时修剪,修剪一段时间后,李师傅有事离开,只留下王师傅一人修剪。在下面四幅图中,图( )能表示修剪时间t和修剪面积S之间的关系。
A. B.
C. D.
5.有两个不是0的自然数,它们之间的关系为,这两个数的最小公倍数是( )。
A. B. C.0.5 D.4
6.把7克糖溶解在100克水中,水占糖水的( )。
A. B. C. D.
7.,变形的依据是( )。
A.加法交换律 B.加法结合律 C.加法交换律和加法结合律 D.以上都不对
8.甲、乙两根绳子同样长,甲绳用去米,乙绳用去后,剩下的绳子相比,( )。
A.甲绳长 B.乙绳长 C.同样长 D.无法确定哪根长
二、填空题
9.,这样计算的依据是( )。
10.某班有的学生喜欢跳绳,的学生喜欢踢毽子,其他学生喜欢球类运动。这个班喜欢球类运动的学生占( )。
11.看图填空。
(1)
( )个番茄和一个萝卜同样重。
(2)
一个苹果和( )个草莓同样重。
12.快、慢两辆汽车分别从甲、乙两地同时相对开出,2小时后在距离中点20千米的地方相遇,快车每小时行驶80千米,慢车的速度是( )千米/时。
13.从0、3、4、5四个数字中任选三个组成三位数,其中能同时被2、3整除的有( )个,能同时被2、3、5整除的有( )。
14.看图回答问题。
(1)纵轴上每个单位长度表示( )摄氏度。
(2)甲市和乙市这一天( )时气温相差最大,( )时气温相差最小。
(3)根据这一天各个时刻的气温可以求出,甲市这一天的平均气温是( )摄氏度。
三、判断题
15.1米的和4米的一样长。( )
16.大于且小于的分数只有一个。( )
17.两个以上异分母分数相加减只能通分一次。( )
18.0.5是方程3x+0.7=1.6的解。( )
19.等式两边同时加上或减去一个数,所得结果仍然是等式。( )
四、计算题
20.直接写出得数。
21.计算下面各题,能简算的要简算。
22.解方程。
25x-16x=270 4+2x=6.2
1.8x÷3=2.4 3×0.9+4x=22.7
五、解答题
23.公路一边共有水杉树52棵,原来每相邻两棵树之间的距离都是8米,现在因树长大了显得较密,要把每相邻两棵树之间的距离改成12米。如果起点的树不移动,那么不需要移动的树还有多少棵?
24.4年前姐姐的年龄是弟弟的2倍,今年姐姐12岁。今年弟弟几岁?(只列方程,不解答)
25.甲、乙两人沿着400米长的环形跑道跑步,他们同时从同一地点出发,同向而行。甲的速度是200米/分,乙的速度是160米/分。经过多少分钟甲第二次追上乙?
26.敏敏参加60米短跑训练,第一周训练时平均每次用时分钟,第二周训练时平均每次用时分钟。第二周比第一周的训练成绩是提高了还是退步了?
27.五(1)班乒乓球组的人数占全班人数的,美术组的人数占全班人数的,没有人同时参加乒乓球组和美术组。
(1)美术组和乒乓球组的人数共占全班人数的几分之几?
(2)乒乓球组的人数比美术组的人数多占全班人数的几分之几?
28.小明选了些饱满的蒜瓣种在两个盆里,分别标注1号盆和2号盆。1号盆放在室外,2号盆放在室内。从第6天开始,每两天一次,测量两盆蒜瓣中长出的最长叶片长,进行记录。下表是前16天记录的数据,请根据记录情况完成问题。
蒜叶生长情况记录表
第6天 第8天 第10天 第12天 第14天 第16天
1号盆最长叶片长/毫米 8 21 42 55 75 100
2号盆最长叶片长/毫米 5 10 22 30 45 60
(1)根据记录的数据完成统计图。
(2)在室外和室内,蒜叶生长变化情况有什么相同点和不同点?
(3)你还能从数据中获得哪些信息?
《第1-5单元必考题检测卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B C C B C C D
1.C
【分析】含有等号的式子叫做等式。含有未知数的等式叫做方程。
方程一定是等式,等式不一定是方程。所以等式包含方程。
【详解】等式与方程的关系可以用下图表示:
故答案为:C
2.B
【分析】用方程解决问题的关键是找到等量关系。从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多(4+4)千克,设乙筐千克,根据甲筐质量-乙筐质量=甲筐比乙筐多的质量,乙筐质量+甲筐比乙筐多的质量=甲筐质量,乙筐质量+甲筐放入乙筐的质量=甲筐质量-甲筐放入乙筐的质量,可以列出方程。
【详解】A.,等量关系:甲筐质量-乙筐质量=甲筐比乙筐多的质量,方程正确;
B.,等量关系:乙筐质量+甲筐放入乙筐的质量≠甲筐质量,方程错误;
C.,等量关系:乙筐质量+甲筐比乙筐多的质量=甲筐质量,方程正确;
D.,等量关系:乙筐质量+甲筐放入乙筐的质量=甲筐质量-甲筐放入乙筐的质量,方程正确。
方程错误的是。
故答案为:B
3.C
【分析】由题意可知,苹果和梨一样多,一家人每天吃4个苹果和3个梨。过了几天,苹果刚好吃完,梨还剩8个。设已经吃了x天,根据苹果吃掉的总数-吃掉梨的总数=8个,列方程计算即可得解。
【详解】解:设已经吃了x天。
4x-3x=8
解得x=8
已经吃了8天。
故答案为:C
4.C
【分析】分析题目,开始时李师傅和王师傅两人一起修剪,根据修剪总面积=单位时间的修剪面积×修剪时间可知,S随着t的增长而增长较快,即直线比较陡峭;后面李师傅离开后,只剩下王师傅一个人修剪,此时S随着t的增长而增长的较慢,即直线比较平缓,据此解答即可。
【详解】
根据分析可知,能表示修剪时间t和修剪面积S之间的关系。
故答案为:C
5.B
【分析】由a÷0.5=b,可得a=0.5b,也就是b=2a,说明b是a的整数倍;求两个数为倍数关系时的最小公倍数:两个数为倍数关系,最小公倍数为较大的数;由此解答问题即可。
【详解】由a÷0.5=b,可得a=0.5b,则,b=2a,
也就是a和b成倍数关系,a和b的最小公倍数为b。
即,有两个不是0的自然数,它们之间的关系为a÷0.5=b,这两个数的最小公倍数是b。
故答案为:B
6.C
【分析】,要先求出糖水的质量,再根据求一个数是另一个数的几分之几用除法计算,求出水占糖水的几分之几。
【详解】7+100=107(克)
100÷107=
所以水占糖水的。
故答案为:C
7.C
【分析】观察算式,发现有2个分母为12的分数,可以把它们先加,这样计算更简便;根据加法交换律a+b=b+a、加法结合律(a+b)+c=a+(b+c)把算式变成进行简算。
【详解】
所以,,变形的依据是加法交换律和加法结合律。
故答案为:C
8.D
【分析】分别将两根绳子的长度看作单位“1”,因为绳子长度不确定,无法确定乙绳用去的长度,也无法确定两根绳子剩下的长度,因此无法进行比较,举例说明即可。
举例求剩下绳子长度的方法:甲绳:绳子长度-甲绳用的长度=甲绳剩下的长度;乙绳:根据分数的意义,分母表示平均分的份数,分子表示取走的份数,绳子长度÷分母×分子=用去的长度,绳子长度-乙绳用的长度=乙绳剩下的长度。
【详解】假设两根绳子都是1米。
1米的是米,1-=(米)
如果两根绳子都是1米,则剩下的绳子相比,同样长。
假设两根绳子都是2米。
甲:2-=(米)
乙:2÷2×1=1(米)
2-1=1(米)
>1,如果两根绳子都是2米,剩下的绳子相比,甲绳长。
假设两根绳子都是0.8米。
甲:0.8-=0.8-0.5=0.3(米)
乙:0.8÷2×1=0.4(米)
0.8-0.4=0.4(米)
0.3<0.4,如果两根绳子都是0.8米,剩下的绳子相比,乙绳长。
因此无法确定哪根长。
故答案为:D
9.减法的性质
【分析】计算时,可以根据减法的性质a-b-c=a-(b+c)把算式变成进行简算。
【详解】,这样计算的依据是(减法的性质)。
10.
【分析】把全班学生的人数看作单位“1”,根据减法的意义,用“1”减去喜欢跳绳、喜欢踢毽子的学生占全班人数分率之和,即是这个班喜欢球类运动的学生占全班人数的几分之几。
【详解】1-(+)
=1-(+)
=1-
=
这个班喜欢球类运动的学生占。
11.(1)3
(2)8
【分析】(1)从图中可知,两个萝卜的重量=一个萝卜和三个番茄的重量,根据等式的性质1将等式的两边同时减去一个萝卜,等式仍然成立。
(2)一个苹果和2个草莓的质量=10个草莓的质量,则将等式的两边同时减两个草莓等式仍然成立。
【详解】(1)1个萝卜的重量+1个萝卜-1个萝卜=一个萝卜+三个番茄-1个萝卜
则3个番茄和一个萝卜同样重。
(2)一个苹果+2个草莓的质量-2个草莓=10个草莓的质量-2个草莓
一个苹果和8个草莓同样重。
12.60
【分析】因为2小时后在距离中点20千米的地方相遇,这意味着快车超过中点20千米,而慢车距离中点还有20千米。所以在这2小时内,快车比慢车多行驶的路程就是这两个20千米,即20×2=40千米;设慢车的速度是x千米/小时,根据速度差×时间=路程差列方程解答即可。
【详解】解:设慢车的速度是x千米/小时。
(80-x)×2=20×2
(80-x)×2=40
(80-x)×2÷2=40÷2
80-x=20
80-x+x=20+x
20+x=80
20+x-20=80-20
x=60
所以慢车的速度是60千米/小时。
13. 5 540、450
【分析】能被2整除的数:个位数是0、2、4、6、8,即偶数。
能被3整除的数:各位数字之和能被3整除。
能被5整除的数:个位数是0或5。
则同时被2和3整除的三位数:个位是偶数(0或4),且各位数字之和能被3整除。
同时被2、3、5整除的三位数:个位为0,且各位数字之和能被3整除。
【详解】同时被2和3整除的三位数
组合分析:组合0、3、4:无符合条件的三位数。
组合0、3、5:无符合条件的三位数。
组合0、4、5:可组成450(和9)、540(和9)、504(和9),共3个。
组合3、4、5:可组成354(和12)、534(和12),共2个。
则其中能同时被2、3整除的有5个;
同时被2、3、5整除的三位数
组合分析:组合0、4、5:可组成450(和9)、540(和9),共2个。
能同时被2、3、5整除的有450、540;
14.(1)5
(2) 6 22
(3)16.6
【分析】(1)纵轴表示气温,观察纵轴即可确定每个单位长度表示的温度;
(2)分别计算每个时刻的气温差,比较即可;
(3)根据平均数=总数量÷总份数,列式计算即可。
【详解】(1)纵轴上每个单位长度表示5摄氏度。
(2)14-7=7(摄氏度)、18-12=6(摄氏度)、24-18=6(摄氏度)、
16-10=6(摄氏度)、11-7=4(摄氏度)
7>6>4
甲市和乙市这一天6时气温相差最大,22时气温相差最小。
(3)(14+18+24+16+11)÷5
=83÷5
=16.6(摄氏度)
甲市这一天的平均气温是16.6摄氏度。
15.√
【分析】1米的,表示把1米看作单位“1”,平均分成7份,取其中的4份,即是米;
4米的,表示把4米看作单位“1”,平均分成7份,取其中的1份,即是米;
据此判断。
【详解】1米的和4米的都表示米,所以1米的和4米的一样长。
原题说法正确。
故答案为:√
16.×
【分析】大于而小于的同分母分数有;如果根据分数的基本性质,、的分子、分母都乘2就是、,大于而小于的分数有、、3个分数;、的分子分母都乘3就是、,大于而小于的分数有、、、、5个分数;、的分子、分母都乘4、5、6它们之间的分数有无数个。
【详解】据分析可知,大于且小于的分数有无数个。原题说法错误。
故答案为:×
17.×
【分析】把异分母分数化成和原来分数相等的同分母分数,叫做通分。
异分母分数的加减法,先通分,然后按照同分母分数的加减法进行计算。多个异分母分数相加减时,可以一次通分,也可以多次分步通分。
【详解】如:-+
=-+
=+
=+
=
通分了两次。
所以,两个以上异分母分数相加减可以多次分步通分,也可以一次通分。
原题说法错误。
故答案为:×
18.×
【分析】分析题目,先根据等式的基本性质求出3x+0.7=1.6的解,再判断即可。
【详解】3x+0.7=1.6
解:3x+0.7-0.7=1.6-0.7
3x=0.9
3x÷3=0.9÷3
x=0.3
所以,x=0.3是方程3x+0.7=1.6的解;原说法错误。
故答案为:×
19.×
【分析】根据等式的基本性质,等式两边同时加上或减去同一个数,左右两边仍然相等。
【详解】题目中“一个数”没有说明是同一个数,如1+3=4;1+3-2≠4-1;所以等式两边同时加上或减去一个相同的数,所得结果才是等式。原题干说法错误。
故答案为:×
20.;;1;0;
;;;
【详解】略
21.;;;
【分析】(1)先把三个分数通分成分母是10的分数,再从左往右依次计算;
(2)根据减法的性质,把原式改写为简算;
(3)根据“去括号”的方法,把原式改写为简算;
(4)运用“带着符号搬家”的方法和减法的性质,把原式改写为简算。
【详解】
=
=0+
=
22.x=30;x=1.1
x=4;x=5
【分析】(1)仔细观察方程及数据特点可知,先计算25x减去16x的结果。25x-16x=9x,然后在方程两边同时除以9即可解方程。
(2)仔细观察方程及数据特点可知,方程两边同时减去4先算出2x的值,然后在方程两边同时除以2即可解方程。
(3)仔细观察方程及数据特点可知,方程两边同时乘3先算出1.8x的值,然后在方程两边同时除以1.8即可解方程。
(4)仔细观察方程及数据特点可知,先计算出3乘0.9的结果。3×0.9=2.7,方程两边同时减去2.7算出4x的值,然后在方程两边同时除以4即可解方程。
【详解】25x-16x=270
解:9x=270
9x÷9=270÷9
x=30
4+2x=6.2
解:4+2x-4=6.2-4
2x=2.2
2x÷2=2.2÷2
x=1.1
1.8x÷3=2.4
解:1.8x÷3×3=2.4×3
1.8x=7.2
1.8x÷1.8=7.2÷1.8
x=4
3×0.9+4x=22.7
解:2.7+4x=22.7
2.7+4x-2.7=22.7-2.7
4x=20
4x÷4=20÷4
x=5
23.17棵
【分析】分析题目,先根据52棵树之间有(52-1)个间隔,用间隔数乘8求出公路的总长度,再求出8和12的最小公倍数是24,即每隔24米的长度对应的树是不需要移动的,据此用公路的总长度除以24即可解答。
【详解】(52-1)×8
=51×8
=408(米)
8和12的最小公倍数是24,
408÷24=17(棵)
答:不需要移动的树有17棵。
24.解:设今年弟弟x岁。
2(x-4)=12-4
【分析】求一个数的几倍是多少用乘法,设今年弟弟x岁,根据(今年弟弟的年龄-4)×2=今年姐姐的年龄-4,列出方程即可。
【详解】解:设今年弟弟x岁。
2(x-4)=12-4
2x-8=8
2x-8+8=8+8
2x=16
2x÷2=16÷2
x=8
答:今年弟弟8岁。
25.20分钟
【分析】甲、乙两人沿着环形跑道跑步,他们同时从一地点出发,同向而行,甲第一次追上乙,需要比乙一共多跑整整一圈400米;第二次追上乙要多跑整整两圈,即400×2=800米。也就是两人的路程差相差800米,设经过x分钟甲第二次追上乙;根据路程=速度×时间;用甲每分钟的速度×x分钟,求出甲x分钟跑的路程;用乙每分钟跑的路程×x,求出乙x分钟跑的路程,再用甲跑的路程-乙跑的路程=两人路程差,列方程:200x-160x=400×2,解方程,即可解答。
【详解】解:设经过x分钟甲第二次追上乙。
200x-160x=400×2
200x-160x=800
40x=800
40x÷40=800÷40
x=20
答:经过20分钟甲第二次追上乙。
【点睛】理解在环形跑道追及问题中,若两人同时同向出发,快着第几次追上慢者,就需要比慢者多跑几个全程是解答本题的关键。
26.退步了
【分析】根据题意,比较两周训练时平均每次所用的时间即可,所用时间越短,成绩越好。
异分母分数比较大小,先通分成分母相同的分数,再按照同分母分数的比较方法比较大小。据此解答。
【详解】=
=
<,则<。
答:第二周比第一周的训练成绩退步了。
27.(1)
(2)
【分析】(1)用加法求出乒乓球组、美术组的人数占全班人数的分率之和,即是美术组和乒乓球组的人数共占全班人数的几分之几。
(2)用乒乓球组的人数占全班人数的分率减去美术组的人数占全班人数的分率,即是乒乓球组的人数比美术组的人数多占全班人数的几分之几。
【详解】(1)
答:美术组和乒乓球组的人数共占全班人数的。
(2)
答:乒乓球组的人数比美术组的人数多占全班人数的。
28.(1)见详解
(2)相同点:蒜叶中的最长叶片的长度都在逐渐变长;不同点:在室外生长的蒜叶长得快一些
(3)第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米
【分析】(1)根据统计表中的数据将折线统计图补充完整即可。
(2)由统计图可知,表示两个盆蒜叶生长情况的折线一直在上升,说明两个盆中的蒜叶一直在生长;而1号盆对应的折线更陡一些,说明1号盆蒜叶生长快一些,2号盆蒜叶生长慢一些。
(3)根据统计表和统计图获取相关的数学信息即可。如:第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米
【详解】
(1)
(2)答:相同点:蒜叶中的最长叶片的长度都在逐渐变长;不同点:在室外生长的蒜叶长得快一些。
(3)答:第16天时,1号盆蒜叶中的最长叶片是100毫米,2号盆蒜叶中的最长叶片是60毫米。(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
