2024-2025学年北京市朝阳区青苗学校高二下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年北京市朝阳区青苗学校高二下学期期中考试数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 21:15:37 | ||
图片预览


文档简介
2024-2025学年北京市朝阳区青苗学校高二下学期期中考试
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某女生有件不同颜色的衬衣,件不同花样的裙子,另有套不同样式的连衣裙,“五一”节选择一套服装参加歌舞演出,则不同的选择方式有( )
A. 种 B. 种 C. 种 D. 种
2.已知函数,则的导函数为( )
A. B.
C. D.
3.名学生报名参加数学、计算机、航模兴趣小组,若每个项目都有人报名,每人限报个项目,则不同的报名方式有种
A. B. C. D.
4.函数的单调递增区间是( )
A. B.
C. D. 和
5.设,为两个事件,若,,则等于( )
A. B. C. D.
6.已知随机变量的分布规律为,则( )
A. B. C. D.
7.二项式的展开式中的常数项为( )
A. B. C. D.
8.已知小明射箭命中靶心的概率为,且每次射击互不影响,则小明在射击次后,恰好命中两次的概率是( )
A. B. C. D.
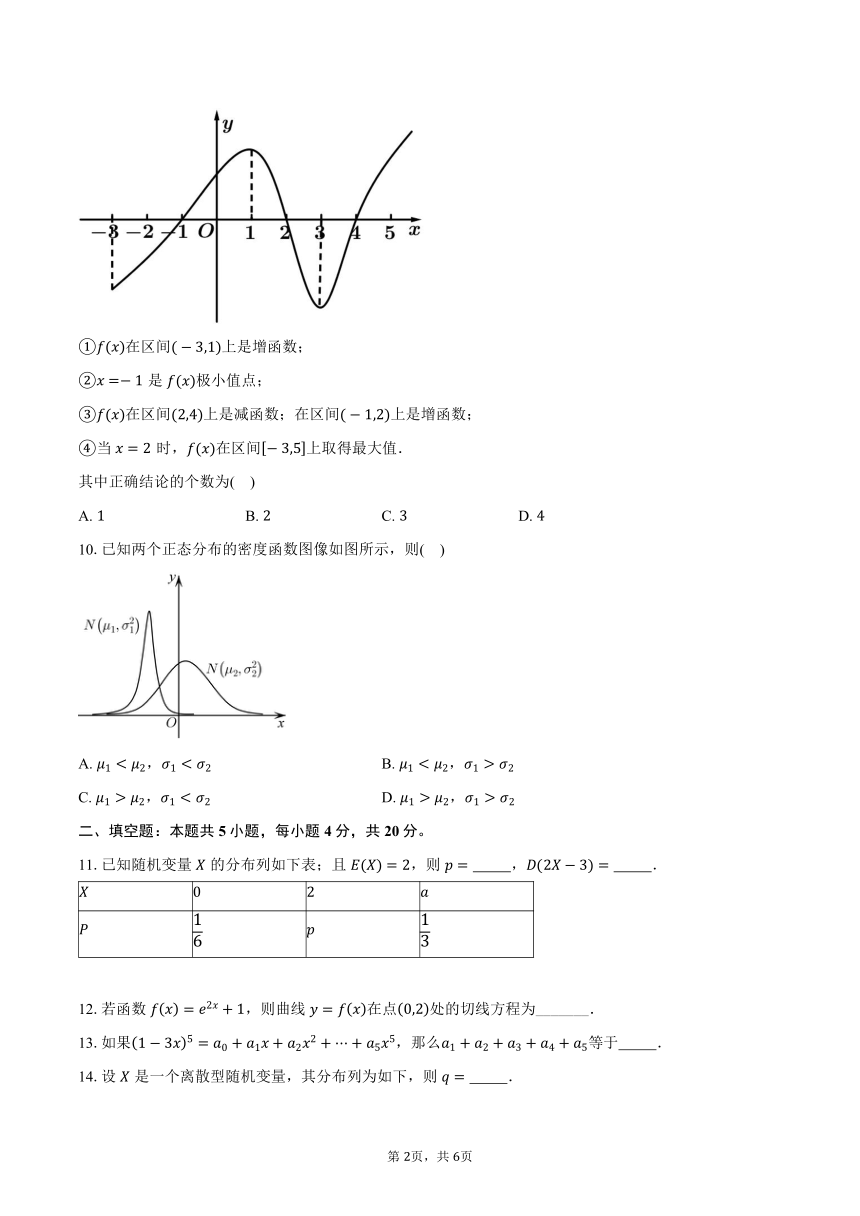
9.如图所示是的导函数的图象,下列个结论:
在区间上是增函数;
是极小值点;
在区间上是减函数;在区间上是增函数;
当时,在区间上取得最大值.
其中正确结论的个数为( )
A. B. C. D.
10.已知两个正态分布的密度函数图像如图所示,则( )
A. , B. ,
C. , D. ,
二、填空题:本题共5小题,每小题4分,共20分。
11.已知随机变量的分布列如下表;且,则 , .
12.若函数,则曲线在点处的切线方程为_______.
13.如果,那么等于 .
14.设是一个离散型随机变量,其分布列为如下,则 .
15.将一枚均匀的硬币连续抛掷次,以表示没有出现连续次正面的概率给出下列四个结论:
;
;
当时,;
.
其中,所有正确结论的序号是 .
三、解答题:本题共4小题,共40分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知函数的图象在点处的切线方程是
求函数的解析式
求函数的单调区间与极值.
17.本小题分
抽样检查是日常检测中常用的方法.某商场进了一种商品件,其中有件次品,若从中抽取件.
抽出的商品中无次品的抽法有多少种?
抽出的商品中全是次品的抽法有多少种?
抽出的商品中至多有件次品的抽法有多少种?
18.本小题分
已知,.
求的值;
求的值;
19.本小题分
某工厂生产一种产品,产品等级分为一等品、二等品、普通品,为了解各等级产品的比例,检测员从流水线上随机抽取件产品进行等级检测,检测结果如下表所示.
产品等级 一等品 二等品 普通品
样本数量件
若从流水线上随机抽取一件产品,估计该产品为一等品的概率;
从该流水线上随机抽取件产品,记其中一等品的件数为,用频率估计概率,求随机变量的分布列和数学期望;
为拓宽市场,工厂决定对抽取的件样本产品进行让利销售,每件产品的销售价格均降低了元.设降价前后这件样本产品的利润的方差分别为,,比较,的大小.请直接写出结论
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.由题意可知,
由,则,
已知函数图像在处的切线方程是,即,
所以,
解得,
的解析式为:,
综上所述,的解析式为;
由可知,的解析式为
则,
令,解得或,
令,解得或,
则函数在和上单调递增
令,解得,则函数在上单调递减,
所以函数在处取得极大值,;在处取得极小值,,
综上所述的单调增区间为和,的单调减区间为,
极大值为,极小值为.
17.由题意,共有件非次品,则抽出的商品中无次品的抽法有种;
由题意,抽出的商品中全是次品的抽法有种;
由题意,抽出的商品中至多有件次品的抽法有种
18.因为,,
令得,.
因为,,
令得,,
令得,,
上述两个等式相减得,故.
19.解:Ⅰ根据题意,样本共有件,其中一等品有件,
则其概率;
Ⅱ根据题意,,
则,
,
,
;
其分布列为:
则有,
Ⅲ根据题意,每件产品的销售价格均降低了元,产品的平均售价也降低了元,
则.
第1页,共1页
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某女生有件不同颜色的衬衣,件不同花样的裙子,另有套不同样式的连衣裙,“五一”节选择一套服装参加歌舞演出,则不同的选择方式有( )
A. 种 B. 种 C. 种 D. 种
2.已知函数,则的导函数为( )
A. B.
C. D.
3.名学生报名参加数学、计算机、航模兴趣小组,若每个项目都有人报名,每人限报个项目,则不同的报名方式有种
A. B. C. D.
4.函数的单调递增区间是( )
A. B.
C. D. 和
5.设,为两个事件,若,,则等于( )
A. B. C. D.
6.已知随机变量的分布规律为,则( )
A. B. C. D.
7.二项式的展开式中的常数项为( )
A. B. C. D.
8.已知小明射箭命中靶心的概率为,且每次射击互不影响,则小明在射击次后,恰好命中两次的概率是( )
A. B. C. D.
9.如图所示是的导函数的图象,下列个结论:
在区间上是增函数;
是极小值点;
在区间上是减函数;在区间上是增函数;
当时,在区间上取得最大值.
其中正确结论的个数为( )
A. B. C. D.
10.已知两个正态分布的密度函数图像如图所示,则( )
A. , B. ,
C. , D. ,
二、填空题:本题共5小题,每小题4分,共20分。
11.已知随机变量的分布列如下表;且,则 , .
12.若函数,则曲线在点处的切线方程为_______.
13.如果,那么等于 .
14.设是一个离散型随机变量,其分布列为如下,则 .
15.将一枚均匀的硬币连续抛掷次,以表示没有出现连续次正面的概率给出下列四个结论:
;
;
当时,;
.
其中,所有正确结论的序号是 .
三、解答题:本题共4小题,共40分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知函数的图象在点处的切线方程是
求函数的解析式
求函数的单调区间与极值.
17.本小题分
抽样检查是日常检测中常用的方法.某商场进了一种商品件,其中有件次品,若从中抽取件.
抽出的商品中无次品的抽法有多少种?
抽出的商品中全是次品的抽法有多少种?
抽出的商品中至多有件次品的抽法有多少种?
18.本小题分
已知,.
求的值;
求的值;
19.本小题分
某工厂生产一种产品,产品等级分为一等品、二等品、普通品,为了解各等级产品的比例,检测员从流水线上随机抽取件产品进行等级检测,检测结果如下表所示.
产品等级 一等品 二等品 普通品
样本数量件
若从流水线上随机抽取一件产品,估计该产品为一等品的概率;
从该流水线上随机抽取件产品,记其中一等品的件数为,用频率估计概率,求随机变量的分布列和数学期望;
为拓宽市场,工厂决定对抽取的件样本产品进行让利销售,每件产品的销售价格均降低了元.设降价前后这件样本产品的利润的方差分别为,,比较,的大小.请直接写出结论
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.由题意可知,
由,则,
已知函数图像在处的切线方程是,即,
所以,
解得,
的解析式为:,
综上所述,的解析式为;
由可知,的解析式为
则,
令,解得或,
令,解得或,
则函数在和上单调递增
令,解得,则函数在上单调递减,
所以函数在处取得极大值,;在处取得极小值,,
综上所述的单调增区间为和,的单调减区间为,
极大值为,极小值为.
17.由题意,共有件非次品,则抽出的商品中无次品的抽法有种;
由题意,抽出的商品中全是次品的抽法有种;
由题意,抽出的商品中至多有件次品的抽法有种
18.因为,,
令得,.
因为,,
令得,,
令得,,
上述两个等式相减得,故.
19.解:Ⅰ根据题意,样本共有件,其中一等品有件,
则其概率;
Ⅱ根据题意,,
则,
,
,
;
其分布列为:
则有,
Ⅲ根据题意,每件产品的销售价格均降低了元,产品的平均售价也降低了元,
则.
第1页,共1页
同课章节目录
