北师大版六年级数学下册第四单元正比例和反比例高频易错题检测卷一(含解析)
文档属性
| 名称 | 北师大版六年级数学下册第四单元正比例和反比例高频易错题检测卷一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 303.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 15:50:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版六年级数学下册第四单元正比例和反比例高频易错题检测卷一
一、填空题(共20分)
1.(2分)测量小组的同学测得一棵大树的影长是7.2米,同时把2米长的竹竿直立在地上,测得它的影长1.8米,这棵树高( )米。
2.(2分)某厂要生产一批豆浆机,平均每天产量和所需时间如下表:
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成( )比例。(填“正”或“反”)
(2)现要在20天内完成生产任务,平均每天产量至少要达到( )台。
3.(2分)给一间教室铺地砖,如采用0.3平方米的地砖,需要400块;如改用0.8平方米的地砖,需要( )块。
4.(2分)如果x和y是两个相关联的量,且,那么x和y成( )比例关系。
5.(2分)如果(m,n均不为0),那么m与n成( )比例,=( )。
6.(2分)表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填( );如果A和B成反比例关系,那么应填( )。
A 3 6
B 7
7.(2分)判断下题中的两个量是否成比例,成什么比例,在括号里填一填。
(1)平行四边形的面积一定,平行四边形的底和高。( )
(2)圆的直径和周长。( )
8.(2分)下图是两个相互咬合的齿轮,大齿轮的半径是3dm,小齿轮的半径是3cm,如果大齿轮转动100周,小齿轮要转动( )周。
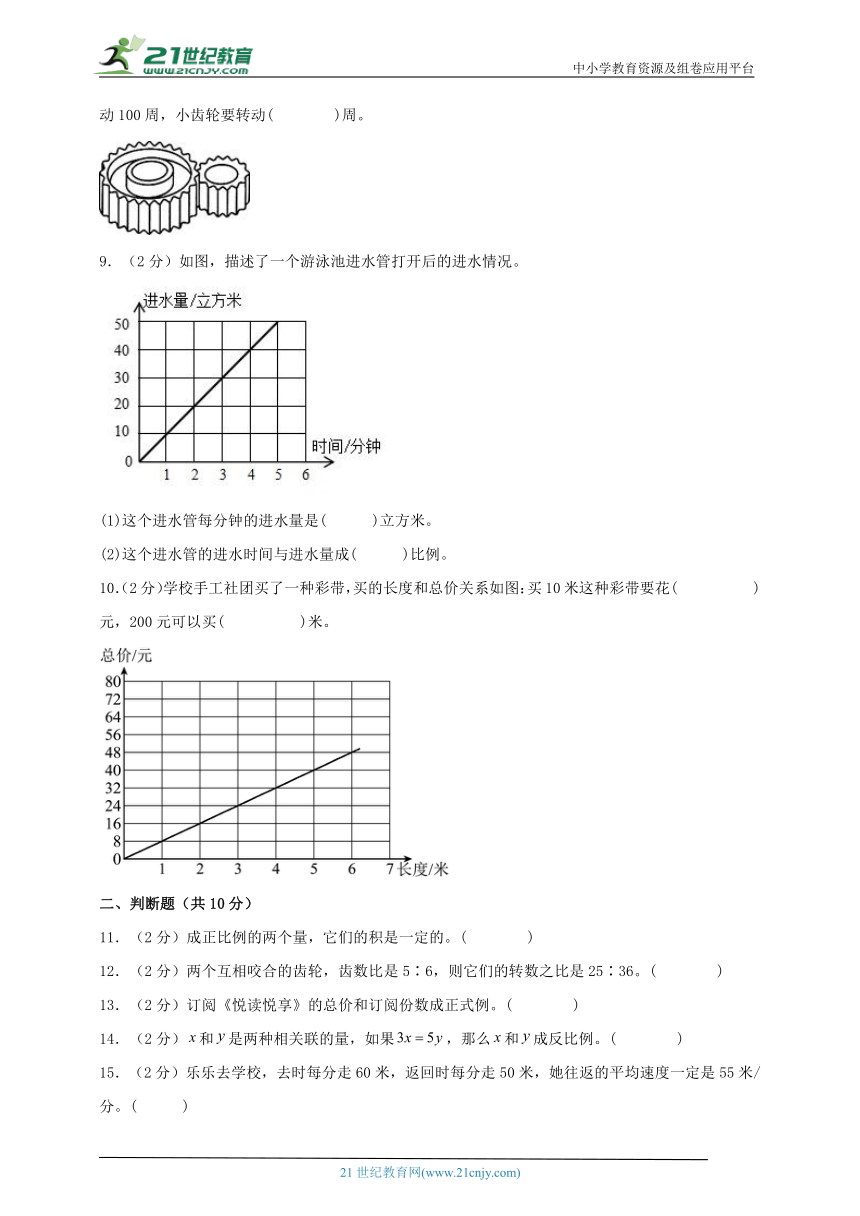
9.(2分)如图,描述了一个游泳池进水管打开后的进水情况。
(1)这个进水管每分钟的进水量是( )立方米。
(2)这个进水管的进水时间与进水量成( )比例。
10.(2分)学校手工社团买了一种彩带,买的长度和总价关系如图:买10米这种彩带要花( )元,200元可以买( )米。
二、判断题(共10分)
11.(2分)成正比例的两个量,它们的积是一定的。( )
12.(2分)两个互相咬合的齿轮,齿数比是5∶6,则它们的转数之比是25∶36。( )
13.(2分)订阅《悦读悦享》的总价和订阅份数成正式例。( )
14.(2分)和是两种相关联的量,如果,那么和成反比例。( )
15.(2分)乐乐去学校,去时每分走60米,返回时每分走50米,她往返的平均速度一定是55米/分。( )
三、选择题(共10分)
16.(2分)一列火车,4小时行320千米。照这样的速度,从甲城到乙城有420千米,( )小时可以到达?如果火车速度提高5%,( )小时就可以到达。( )
A.2.25;2 B.8.25;8 C.5.25;5 D.6.25;4
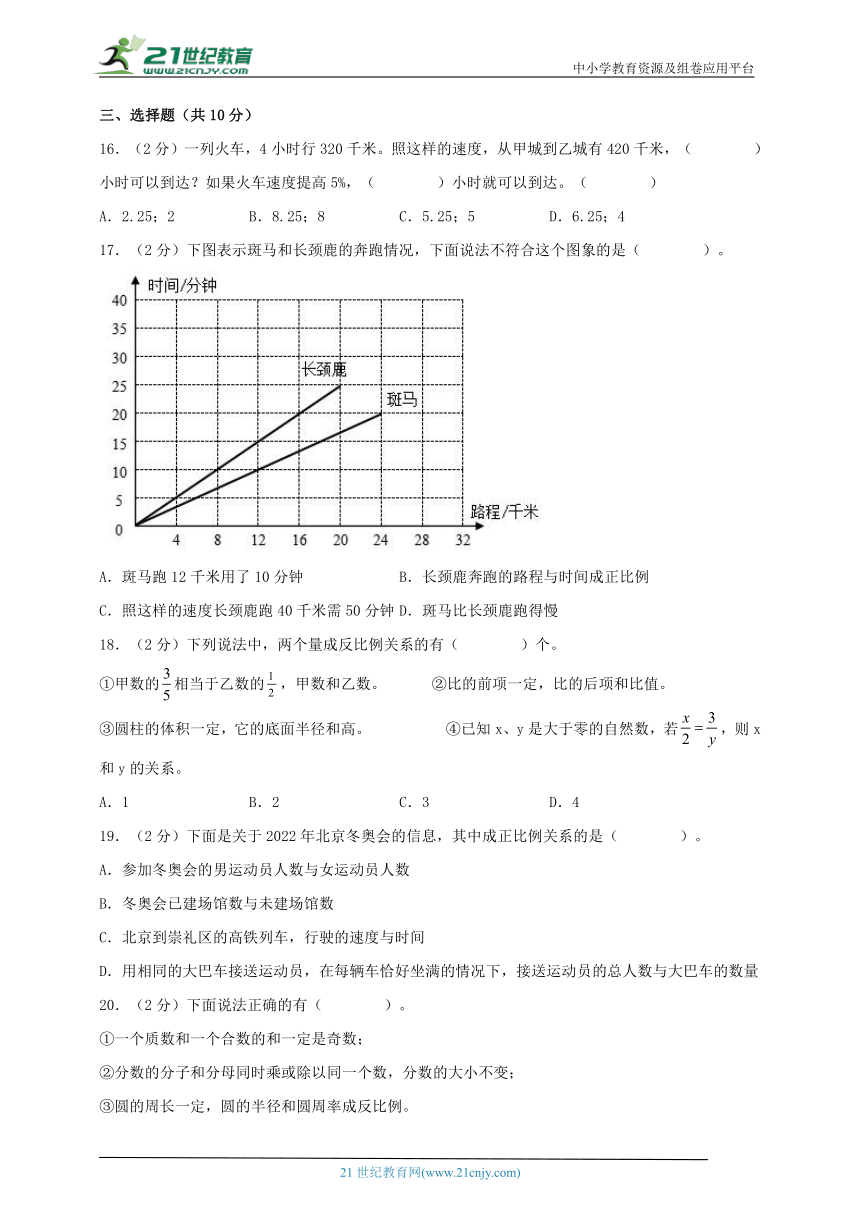
17.(2分)下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是( )。
A.斑马跑12千米用了10分钟 B.长颈鹿奔跑的路程与时间成正比例
C.照这样的速度长颈鹿跑40千米需50分钟 D.斑马比长颈鹿跑得慢
18.(2分)下列说法中,两个量成反比例关系的有( )个。
①甲数的相当于乙数的,甲数和乙数。 ②比的前项一定,比的后项和比值。
③圆柱的体积一定,它的底面半径和高。 ④已知x、y是大于零的自然数,若,则x和y的关系。
A.1 B.2 C.3 D.4
19.(2分)下面是关于2022年北京冬奥会的信息,其中成正比例关系的是( )。
A.参加冬奥会的男运动员人数与女运动员人数
B.冬奥会已建场馆数与未建场馆数
C.北京到崇礼区的高铁列车,行驶的速度与时间
D.用相同的大巴车接送运动员,在每辆车恰好坐满的情况下,接送运动员的总人数与大巴车的数量
20.(2分)下面说法正确的有( )。
①一个质数和一个合数的和一定是奇数;
②分数的分子和分母同时乘或除以同一个数,分数的大小不变;
③圆的周长一定,圆的半径和圆周率成反比例。
A.0个 B.1个 C.2个 D.3个
四、作图题(共6分)
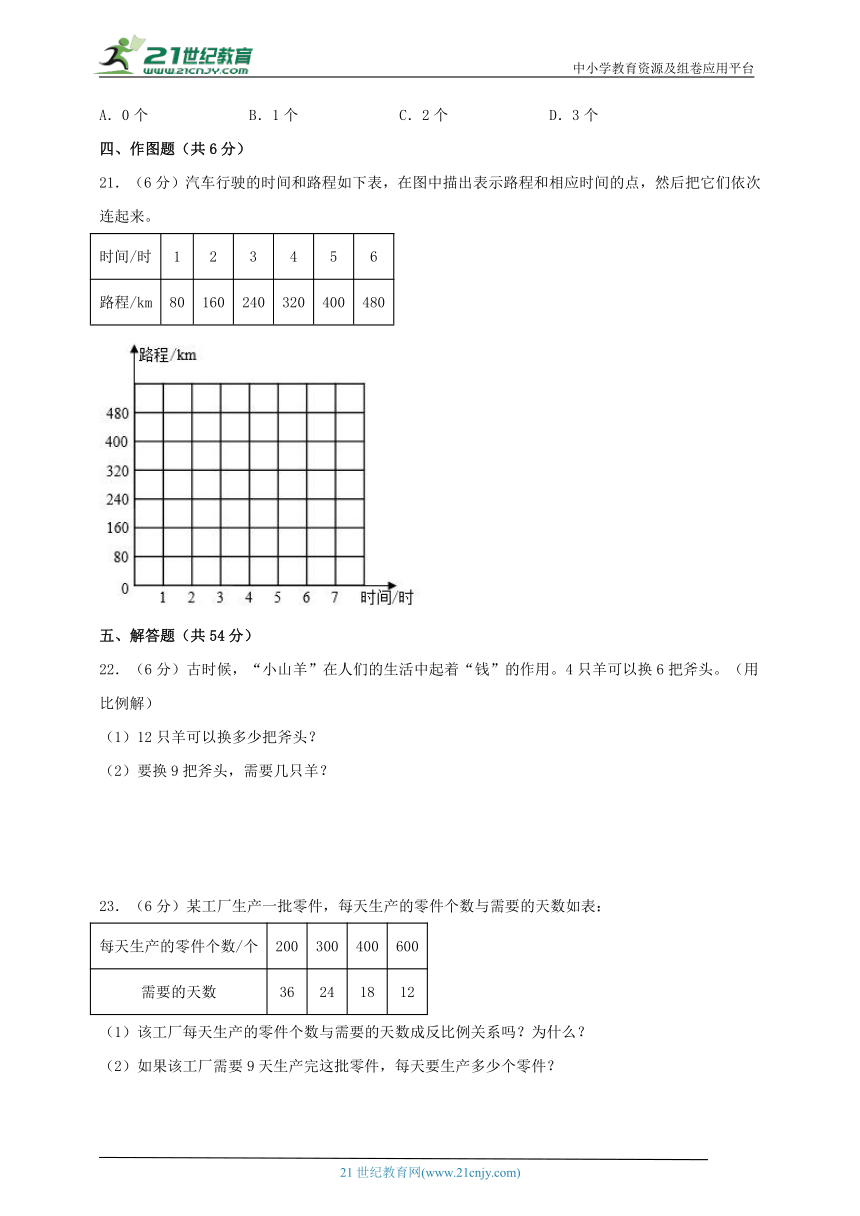
21.(6分)汽车行驶的时间和路程如下表,在图中描出表示路程和相应时间的点,然后把它们依次连起来。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
五、解答题(共54分)
22.(6分)古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
23.(6分)某工厂生产一批零件,每天生产的零件个数与需要的天数如表:
每天生产的零件个数/个 200 300 400 600
需要的天数 36 24 18 12
(1)该工厂每天生产的零件个数与需要的天数成反比例关系吗?为什么?
(2)如果该工厂需要9天生产完这批零件,每天要生产多少个零件?
24.(6分)随着科技的发展和人们网络购物次数的增长,越来越多的购物平台用智能机器人来处理客户订单,已知1台智能机器人30分钟能处理40个订单,照这样的速度,1台智能机器人12小时能处理多少个订单?(用比例解答)
25.(12分)一辆小汽车每时行驶60千米。
时间/时 1 2 3 4 5 6 …
路程/km 60 …
①把表填写完整。
②根据表中数据,在如图中描出时间和路程的对应点,再按顺序连线。
③时间和路程成( )比例。
26.(12分)购买一种丝带的长度和应付金额如下表。
长度 0 1 2 3 4 5 …
应付金额元 0 4 8 12 16 20 …
(1)判断应付金额与长度是否成正比例关系,说明理由。
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接。
(3)购买7.5米丝带需要( )元;76元最多可以购买( )长的丝带。
27.(12分)某喷泉的喷水量与喷水天数情况如表。
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 ( ) ( ) ( )
(1)将上表填写完整。
(2)判断喷水量与喷水天数是否成正比例,并说明理由。
(3)把喷水量与喷水天数所对应的点在图中描出来,并连线。
(4)利用图像估计一下,3.5天的喷水量是( )m3;40万m3的喷水量需要喷( )天。
参考答案
1.8
【分析】根据题意可知,实际长度和影子的长度的比值一定,它们成正比例关系,据此设这棵树高x米,列比例为x∶7.2=2∶1.8,然后解出比例即可。
【详解】解:设这棵树高x米。
x∶7.2=2∶1.8
1.8x=7.2×2
1.8x=14.4
x=14.4÷1.8
x=8
这棵树高8米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
2.(1)反
(2)750
【分析】(1)两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)用统计表中平均每天产量乘对应的天数求出这批生产任务的总台数,再除以20即可解答。
【详解】(1)200×75=15000(台)
300×50=15000(台)
500×30=15000(台)
平均每天产量×所需时间=总台数(一定),平均每天产量和所需时间的乘积一定,则平均每天产量和所需时间成反比例。
(2)15000÷20=750(台),则平均每天产量至少要达到750台。
【点睛】本题考查反比例的辨认和应用。掌握正比例和反比例的意义是解题的关键。
3.150
【分析】设如改用0.8平方米的地砖,需要x块。因为一间教室的地面面积不变,那么,一块地砖的面积×需要的地砖块数=这间教室的面积(一定),所以一块地砖的面积和需要的地砖块数成反比例关系,据此可列比例:0.3×400=0.8x,再算出结果即可求解。
【详解】解:设如改用0.8平方米的地砖,需要x块。
0.8x=400×0.3
0.8x=120
x=120÷0.8
x=150
所以如改用0.8平方米的地砖,需要150块。
【点睛】本题考查反比例的应用,注意:需先判断一块地砖的面积和需要的地砖块数成反比例关系。
4.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5∶x=y∶9,所以xy=5×9;
xy=45(一定),x和y成反比例。
如果x和y是两个相关联的量,且5∶x=y∶9,那么x和y成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
5. 正
【分析】根据比例的基本性质:内项积=外项积,即m∶n=3∶7,由于3∶7=3÷7=,所以m和n的比值一定,根据正比例的判定方法:当两个相关联的量比值一定,则成正比例关系,据此即可填空。
【详解】由于m∶n=3∶7
则m∶n=3÷7=,即=
如果7m=3n(m,n均不为0),那么m与n成正比例,=。
【点睛】本题主要考查比例的基本性质以及正比例的意义,熟练掌握正比例的意义是解题的关键。
6. 14 3.5
【分析】如果A和B成正比例关系,则3与7的比等于6与方框内数的比;如果A和B成反比例关系,则3与7的积等于6与方框内数的积。
【详解】解:设方框内的数为x。
如果A和B成正比例关系,则
3:7=6:x
3x=7×6
3x÷3=42÷3
x=14
表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填14;
如果A和B成反比例关系,则
6x=3×7
6x÷6=21÷6
x=3.5
如果A和B成反比例关系,那么应填3.5。
【点睛】两种相关联的量,若其成正比例关系,则其比值一定;若其成反比例关系,则其乘积一定。
7.(1)反比例
(2)正比例
【分析】判断两个相关联的量成什么比例,就可这两种相关量的量中对应的是比值一定还是乘积一定,如果比值一定,成正比例关系;如果乘积一定,成反比例关系,据此解答。
【详解】(1)平行四边形面积=底×高(一定);底和高成反比例。
(2)圆的周长=π×直径;圆的周长÷直径=π(一定);圆的周长和直径成正比例。
【点睛】根据正比例意义和辨别、反比例意义和辨别进行解答。
8.1000
【分析】因为两个是相互交合的齿轮,即转动齿数相等,所以转动的周数和每周齿数成反比,由此列出比例解决问题。
【详解】3dm=30cm
解:设小齿轮要转动x周。
100×3.14×2×30=3.14×2×3×x
100×2×30=2×3×x
100×30=3×x
3000=3x
x=1000
【点睛】答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例,另外还要注意单位的统一。
9.(1)10
(2)正
【分析】(1)时间从0到5小时,共进水50立方米,用进水量除以时间即可;
(2)由图象可以发现,进水量除以时间是一个定值,符合正比例的判定。
(1)
50÷(5-0)
=50÷5
=10(立方米/分钟)
这个进水管每分钟进水量是10立方米。
(2)
由图象可以发现,进水量除以时间是一个定值,符合正比例的判定;这个进水管的进水量与时间成正比例关系。
【点睛】本题属于辨识两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
10. 80 25
【分析】从图中可以看出总价和买的长度成正比例关系,8元对应的是1米,所以每米需要8元,那么10米就需要(8×10)元,200可以买(200÷8)米。
【详解】8×10=80(元)
200÷8=25(米)
所以买10米这种彩带要花80元,200元可以买25米。
【点睛】此题考查了学生对正比例关系的辨识及应用。
11.×
【分析】根据正比例的意义进行解答,成正比例的两个量中,相对应的两个数的比值是一定的。
【详解】成正比例的两个量,它们的积是一定的。原题说法错误。
故答案为:×
【点睛】此题考查了正比例的意义。要求熟练掌握并灵活运用。
12.×
【分析】根据互相咬合齿轮的转数与齿轮的齿数成反比,即可得出答案。
【详解】因为互相咬合齿轮的转数与齿轮的齿数成反比,所以齿数比是5∶6,则它们的转数之比是6∶5。
故答案为:×
【点睛】解答本题要掌握:齿轮的齿数×转数=转过的总齿数(一定),所以齿轮的转数与齿数成反比例。
13.√
【分析】根据公式:总价÷订阅份数=单价,由于每本《悦读悦享》的价格是固定的,所以单价一定;当两个相关联的量的比值一定,则成正比例关系,据此即可判断。
【详解】由分析可知:
总价÷订阅份数=单价(一定),则订阅《悦读悦享》的总价和订阅份数成正式例。原题说法正确。
故答案为:√
【点睛】本题主要考查正比例的判定方法,熟练掌握它的意义是解题的关键。
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是乘积一定,如果比值一定,就成正比例,如果乘积一定,则成反比例,据此解答。
【详解】3x=5y,所以x∶y=5∶3=(一定),x和y成正比例。
x和y是两种相关联的量,如果3x=5y,那么x和y成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨别,反比例意义和辨别是解答本题的关键。
15.×
【分析】首先根据速度×时间=路程,可得路程一定时,时间和速度成反比,据此求出去时和返回用的时间的比是多少;然后根据路程÷时间=速度,用往返的路程除以往返用的总时间,求出她往返的平均速度是每分钟走多少米即可。
【详解】乐乐去时和返回用的时间的比是:50∶60=5∶6,
设去时用的时间是5t,则返回用的时间是6t,
(60×5t×2)÷(5t+6t)
=600t÷11t
=600÷11
=54(米/分)
故答案为:×
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
16.C
【分析】根据题意可知,路程÷时间=速度(一定),则路程和时间的比值一定,它们成正比例关系,据此设从甲城到乙城有420千米,x小时可以到达,列比例为420∶x=320∶4,然后解出比例即可;先用320÷4求出火车的速度,如果火车速度提高5%,则把原来火车的速度看作单位“1”,现在火车的速度是原来的(1+5%),根据百分数乘法的意义,用原来的速度乘(1+5%)即可求出现在的速度,然后用420千米除以现在火车的速度,即可求出如果火车速度提高5%,几小时就可以到达。
【详解】解:设从甲城到乙城有420千米,x小时可以到达。
420∶x=320∶4
320x=420×4
320x=1680
x=1680÷320
x=5.25
320÷4=80(千米/小时)
80×(1+5%)
=80×1.05
=84(千米/小时)
420÷84=5(小时)
从甲城到乙城有420千米,5.25小时可以到达;如果火车速度提高5%,5小时就可以到达。
故答案为:C
【点睛】本题主要考查了正比例的应用,掌握速度、时间、路程三者之间的关系是解答本题的关键。
17.D
【分析】根据统计图可知,在10分钟的时候,斑马跑了12千米,A选项据此判断;
长颈鹿的奔跑的路程和时间的商一定,也就是速度一定,可以判断长颈鹿奔跑的路程与时间是否成正比例,B选项据此解答;
根据速度=路程÷时间,先计算出长颈鹿的速度,再根据路程=速度×时间,求出长颈鹿50分钟跑的路程,C选项据此判断;
计算出斑马和长颈鹿的速度,再进行比较,即可判断谁跑的快,谁慢,D选项据此解答。
【详解】A.观察统计图可知,斑马跑12千米用了10分钟,原题干说法正确;
B.观察图形可知,长颈鹿奔跑的速度不变,根据路程÷时间=速度(一定),长颈鹿奔跑的路程与时间成正比例,原题干说法正确;
C.20÷25×50
=0.8×50
=40(千米)
照这样的速度长颈鹿跑40千米需50分钟,原题干说法正确;
D.斑马速度:24÷20=1.2(千米)
长颈鹿速度:20÷25=0.8(千米)
1.2千米>0.8千米,长颈鹿跑得慢。
原题干说法错误。
下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是斑马比长颈鹿跑得慢。
故答案为:D
【点睛】本题考查了对成正比例关系图像的认识,根据图像,按要求找出有用的信息进行计算解答本题。
18.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
①根据分数乘法的意义,可知甲数×=乙数×;再根据比例的基本性质:两外项之积等于两内项之积,可知甲数∶乙数=∶,求比值用比的前项除以后项即可;据此可知甲数和乙数的比值一定,则它们成正比例;
②根据比各部分的关系,可知比的后项×比值=比的前项(一定),比的后项和比值的乘积一定,则它们成反比例;
③圆柱的体积公式:S=πr2h,体积一定,底面半径的平方和高的乘积一定,则它们成反比例,但是底面半径和高不成比例;
④根据比和分数的关系,可知x∶2=3∶y,再根据比例的基本性质,可知xy=2×3,x和y的乘积一定,则它们成反比例。
【详解】①甲数的相当于乙数的,甲数和乙数成正比例;
②比的前项一定,比的后项和比值成反比例;
③圆柱的体积一定,它的底面半径和高不成比例;
④已知x、y是大于零的自然数,若,则x和y成反比例。
两个量成反比例关系的有2个,也就是②④。
故答案为:B
【点睛】本题考查了正比例、反比例的意义和辨识,掌握相关判别方法是解答本题的关键。
19.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。据此解答。
【详解】A.男运动员人数+女运动员人数=运动员总人数,参加冬奥会的男运动员人数与女运动员人数的和一定,不成比例;
B.已建场馆数+未建场馆数=冬奥会场馆总数,冬奥会已建场馆数与未建场馆数的和一定,不成比例;
C.速度×时间=路程,北京到崇礼区的路程一定,则高铁列车行驶的速度与时间的积一定,但是比值或商一定,那么行驶的速度与时间不成正比例关系;
D.接送运动员的总人数÷大巴车的数量=每辆大巴车的载客量(一定),则接送运动员的总人数与大巴车数量的商一定,则接送运动员的总人数与大巴车的数量成正比例关系。
故答案为:D
20.A
【分析】只有1和它本身两个因数的数叫做质数;一个数如果除了1和它本身还有别的因数,这样的数叫做合数;整数中,不是2的倍数的数叫做奇数。
分数的基本性质:分子和分母同时乘(或除以)同一个数(0除外),分数大小不变。
圆的周长.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就成反比例关系。
【详解】①×,,6是偶数不是奇数。
②×,分数的分子和分母同时乘或除以同一个数(0除外),分数大小不变。
③×,,周长一定,半径和圆周率都不变,不成比例。
所以说法正确的个数为0个。
故答案为:A
【点睛】考查了质数、合数、奇数的含义;分数的基本性质以及圆的周长公式、反比例的辨别,熟练掌握基础知识是关键。
21.见详解
【分析】根据表格中时间和路程的对应关系,找出相应的点,然后把它们按顺序连起来即可。
【详解】画图如下:
【点睛】此题考查了正比例的意义,即相关联的两种量,如果它们的比值一定,那么这两种量成正比例关系。
22.(1)18把
(2)6只
【分析】(1)由题可知:羊和斧头成正比例关系,设12只羊可以换x把斧头,4与6的比等于12与x的比,据此解答。
(2)设要换9把斧头,需要x只羊,4与6的比等于x与9的比,据此解答。
【详解】(1)解:设12只羊可以换x把斧头。
4∶6=12∶x
4x=6×12
4x=72
4x÷4=72÷4
x=18
答:12只羊可以换18把斧头。
(2)解:设要换9把斧头,需要x只羊。
4∶6=x∶9
6x=4×9
6x=36
x=6
答:需要6只羊。
【点睛】本题主要考查正比例的应用,同时要熟练掌握解比例的方法。
23.(1)该工厂每天生产的零件个数与需要的天数成反比例关系,理由如下:
因为200×36=300×24=400×18=600×12=7200,即每天生产的零件个数×需要的天数=零件总个数(一定),所以每天生产的辆数和所需的天数成反比例关系。
(2)800个
【分析】(1)根据表中数据求出每天生产的零件个数和所需的天数的乘积,再进一步判断即可。
(2)求平均每天要生产多少个零件,用总零件个数(200×36)除以时间9天即可。
【详解】(1)该工厂每天生产的零件个数与需要的天数成反比例关系,理由如下:
因为200×36=300×24=400×18=600×12=7200,即每天生产的零件个数×需要的天数=零件总个数(一定),所以每天生产的辆数和所需的天数成反比例关系。
(2)200×36÷9
=7200÷9
=800(个)
答:平均每天要生产800个零件。
【点睛】此题属于辨识成正、反比例的量以及利用反比例的意义解决实际问题。
24.960个
【分析】设1台智能机器人12小时能处理x份订单,工作效率一定,工作总量和工作时间成正比例,据此列比例解答即可。
【详解】30分钟小时
解:设1台智能机器人12小时能处理x个订单。
0.5x=40×12
0.5x=480
0.5x÷0.5=480÷0.5
答:1台智能机器人12小时能处理960个订单。
25.①见详解
②见详解
③正
【分析】①根据“路程=速度×时间”,代入数据求出路程即可;
②在图中描出各点,再连线即可;
③两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例;时间与路程的比值一定,可知时间与路程成正比例。
【详解】①
60×2=120(千米)
60×3=180(千米)
60×4=240(千米)
60×5=300(千米)
60×6=360(千米)
时间/时 1 2 3 4 5 6 …
路程/km 60 120 180 240 300 360 …
②
③1÷60=2÷120=3÷180=4÷240=5÷300=6÷360=(一定),时间与路程成正比例。
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
26.(1)见详解
(2)见详解
(3)30;19
【分析】(1)如果两个相关联的量的比值一定,那么这两个相关联的量成正比例关系,据此解答即可;
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接即可;
(3)根据1米丝带的价格是4元,用单价×数量=总价,可求出购买7.5米丝带需要多少元;用总价÷单价=数量,可求得76元最多可以购买多长的丝带。
【详解】(1)应付金额与长度成正比例关系。
因为(一定),所以应付金额与长度成正比例关系。
(2)
(3)(元)
(米)
购买7.5米丝带需要30元;76元最多可以购买19长的丝带。
【点睛】熟练掌握正比例关系的定义,是解答此题的关键。
27.(1)48万;64万;80万;
(2)正比例;理由见详解
(3)见详解;
(4)56万立方米;2.5天
【分析】(1)根据喷水天数与喷水量之间的观察完成表格;
(2)计算出表格中喷水量与喷水天数的比值,看比值是否相等;
(3)根据表格中的数据在图中描点、连线。
(4)结合图像进行计算。
【详解】(1)
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 48万 64万 80万
(2)16÷1=32÷2=48÷3=64÷4=80÷5=16(一定)
因为喷水量和喷水天数的比值一定,所以喷水量与喷水天数成正比例;
(3)
(4)3.5×16=56(万立方米)
40÷16=2.5(天)
3.5天的喷水量是56万立方米;40万立方米的喷水量需要喷2.5天。
【点睛】本题考查了成正比例关系的判定、统计表及统计图的填补、从统计表或统计图中读出信息、分析数据、解决问题的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版六年级数学下册第四单元正比例和反比例高频易错题检测卷一
一、填空题(共20分)
1.(2分)测量小组的同学测得一棵大树的影长是7.2米,同时把2米长的竹竿直立在地上,测得它的影长1.8米,这棵树高( )米。
2.(2分)某厂要生产一批豆浆机,平均每天产量和所需时间如下表:
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成( )比例。(填“正”或“反”)
(2)现要在20天内完成生产任务,平均每天产量至少要达到( )台。
3.(2分)给一间教室铺地砖,如采用0.3平方米的地砖,需要400块;如改用0.8平方米的地砖,需要( )块。
4.(2分)如果x和y是两个相关联的量,且,那么x和y成( )比例关系。
5.(2分)如果(m,n均不为0),那么m与n成( )比例,=( )。
6.(2分)表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填( );如果A和B成反比例关系,那么应填( )。
A 3 6
B 7
7.(2分)判断下题中的两个量是否成比例,成什么比例,在括号里填一填。
(1)平行四边形的面积一定,平行四边形的底和高。( )
(2)圆的直径和周长。( )
8.(2分)下图是两个相互咬合的齿轮,大齿轮的半径是3dm,小齿轮的半径是3cm,如果大齿轮转动100周,小齿轮要转动( )周。
9.(2分)如图,描述了一个游泳池进水管打开后的进水情况。
(1)这个进水管每分钟的进水量是( )立方米。
(2)这个进水管的进水时间与进水量成( )比例。
10.(2分)学校手工社团买了一种彩带,买的长度和总价关系如图:买10米这种彩带要花( )元,200元可以买( )米。
二、判断题(共10分)
11.(2分)成正比例的两个量,它们的积是一定的。( )
12.(2分)两个互相咬合的齿轮,齿数比是5∶6,则它们的转数之比是25∶36。( )
13.(2分)订阅《悦读悦享》的总价和订阅份数成正式例。( )
14.(2分)和是两种相关联的量,如果,那么和成反比例。( )
15.(2分)乐乐去学校,去时每分走60米,返回时每分走50米,她往返的平均速度一定是55米/分。( )
三、选择题(共10分)
16.(2分)一列火车,4小时行320千米。照这样的速度,从甲城到乙城有420千米,( )小时可以到达?如果火车速度提高5%,( )小时就可以到达。( )
A.2.25;2 B.8.25;8 C.5.25;5 D.6.25;4
17.(2分)下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是( )。
A.斑马跑12千米用了10分钟 B.长颈鹿奔跑的路程与时间成正比例
C.照这样的速度长颈鹿跑40千米需50分钟 D.斑马比长颈鹿跑得慢
18.(2分)下列说法中,两个量成反比例关系的有( )个。
①甲数的相当于乙数的,甲数和乙数。 ②比的前项一定,比的后项和比值。
③圆柱的体积一定,它的底面半径和高。 ④已知x、y是大于零的自然数,若,则x和y的关系。
A.1 B.2 C.3 D.4
19.(2分)下面是关于2022年北京冬奥会的信息,其中成正比例关系的是( )。
A.参加冬奥会的男运动员人数与女运动员人数
B.冬奥会已建场馆数与未建场馆数
C.北京到崇礼区的高铁列车,行驶的速度与时间
D.用相同的大巴车接送运动员,在每辆车恰好坐满的情况下,接送运动员的总人数与大巴车的数量
20.(2分)下面说法正确的有( )。
①一个质数和一个合数的和一定是奇数;
②分数的分子和分母同时乘或除以同一个数,分数的大小不变;
③圆的周长一定,圆的半径和圆周率成反比例。
A.0个 B.1个 C.2个 D.3个
四、作图题(共6分)
21.(6分)汽车行驶的时间和路程如下表,在图中描出表示路程和相应时间的点,然后把它们依次连起来。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
五、解答题(共54分)
22.(6分)古时候,“小山羊”在人们的生活中起着“钱”的作用。4只羊可以换6把斧头。(用比例解)
(1)12只羊可以换多少把斧头?
(2)要换9把斧头,需要几只羊?
23.(6分)某工厂生产一批零件,每天生产的零件个数与需要的天数如表:
每天生产的零件个数/个 200 300 400 600
需要的天数 36 24 18 12
(1)该工厂每天生产的零件个数与需要的天数成反比例关系吗?为什么?
(2)如果该工厂需要9天生产完这批零件,每天要生产多少个零件?
24.(6分)随着科技的发展和人们网络购物次数的增长,越来越多的购物平台用智能机器人来处理客户订单,已知1台智能机器人30分钟能处理40个订单,照这样的速度,1台智能机器人12小时能处理多少个订单?(用比例解答)
25.(12分)一辆小汽车每时行驶60千米。
时间/时 1 2 3 4 5 6 …
路程/km 60 …
①把表填写完整。
②根据表中数据,在如图中描出时间和路程的对应点,再按顺序连线。
③时间和路程成( )比例。
26.(12分)购买一种丝带的长度和应付金额如下表。
长度 0 1 2 3 4 5 …
应付金额元 0 4 8 12 16 20 …
(1)判断应付金额与长度是否成正比例关系,说明理由。
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接。
(3)购买7.5米丝带需要( )元;76元最多可以购买( )长的丝带。
27.(12分)某喷泉的喷水量与喷水天数情况如表。
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 ( ) ( ) ( )
(1)将上表填写完整。
(2)判断喷水量与喷水天数是否成正比例,并说明理由。
(3)把喷水量与喷水天数所对应的点在图中描出来,并连线。
(4)利用图像估计一下,3.5天的喷水量是( )m3;40万m3的喷水量需要喷( )天。
参考答案
1.8
【分析】根据题意可知,实际长度和影子的长度的比值一定,它们成正比例关系,据此设这棵树高x米,列比例为x∶7.2=2∶1.8,然后解出比例即可。
【详解】解:设这棵树高x米。
x∶7.2=2∶1.8
1.8x=7.2×2
1.8x=14.4
x=14.4÷1.8
x=8
这棵树高8米。
【点睛】本题主要考查了正比例的应用,判断相关的量是正比例还是反比例是解答本题的关键。
2.(1)反
(2)750
【分析】(1)两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
(2)用统计表中平均每天产量乘对应的天数求出这批生产任务的总台数,再除以20即可解答。
【详解】(1)200×75=15000(台)
300×50=15000(台)
500×30=15000(台)
平均每天产量×所需时间=总台数(一定),平均每天产量和所需时间的乘积一定,则平均每天产量和所需时间成反比例。
(2)15000÷20=750(台),则平均每天产量至少要达到750台。
【点睛】本题考查反比例的辨认和应用。掌握正比例和反比例的意义是解题的关键。
3.150
【分析】设如改用0.8平方米的地砖,需要x块。因为一间教室的地面面积不变,那么,一块地砖的面积×需要的地砖块数=这间教室的面积(一定),所以一块地砖的面积和需要的地砖块数成反比例关系,据此可列比例:0.3×400=0.8x,再算出结果即可求解。
【详解】解:设如改用0.8平方米的地砖,需要x块。
0.8x=400×0.3
0.8x=120
x=120÷0.8
x=150
所以如改用0.8平方米的地砖,需要150块。
【点睛】本题考查反比例的应用,注意:需先判断一块地砖的面积和需要的地砖块数成反比例关系。
4.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5∶x=y∶9,所以xy=5×9;
xy=45(一定),x和y成反比例。
如果x和y是两个相关联的量,且5∶x=y∶9,那么x和y成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
5. 正
【分析】根据比例的基本性质:内项积=外项积,即m∶n=3∶7,由于3∶7=3÷7=,所以m和n的比值一定,根据正比例的判定方法:当两个相关联的量比值一定,则成正比例关系,据此即可填空。
【详解】由于m∶n=3∶7
则m∶n=3÷7=,即=
如果7m=3n(m,n均不为0),那么m与n成正比例,=。
【点睛】本题主要考查比例的基本性质以及正比例的意义,熟练掌握正比例的意义是解题的关键。
6. 14 3.5
【分析】如果A和B成正比例关系,则3与7的比等于6与方框内数的比;如果A和B成反比例关系,则3与7的积等于6与方框内数的积。
【详解】解:设方框内的数为x。
如果A和B成正比例关系,则
3:7=6:x
3x=7×6
3x÷3=42÷3
x=14
表中A、B是两个相关联的量,如果A和B成正比例关系,那么应填14;
如果A和B成反比例关系,则
6x=3×7
6x÷6=21÷6
x=3.5
如果A和B成反比例关系,那么应填3.5。
【点睛】两种相关联的量,若其成正比例关系,则其比值一定;若其成反比例关系,则其乘积一定。
7.(1)反比例
(2)正比例
【分析】判断两个相关联的量成什么比例,就可这两种相关量的量中对应的是比值一定还是乘积一定,如果比值一定,成正比例关系;如果乘积一定,成反比例关系,据此解答。
【详解】(1)平行四边形面积=底×高(一定);底和高成反比例。
(2)圆的周长=π×直径;圆的周长÷直径=π(一定);圆的周长和直径成正比例。
【点睛】根据正比例意义和辨别、反比例意义和辨别进行解答。
8.1000
【分析】因为两个是相互交合的齿轮,即转动齿数相等,所以转动的周数和每周齿数成反比,由此列出比例解决问题。
【详解】3dm=30cm
解:设小齿轮要转动x周。
100×3.14×2×30=3.14×2×3×x
100×2×30=2×3×x
100×30=3×x
3000=3x
x=1000
【点睛】答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例,另外还要注意单位的统一。
9.(1)10
(2)正
【分析】(1)时间从0到5小时,共进水50立方米,用进水量除以时间即可;
(2)由图象可以发现,进水量除以时间是一个定值,符合正比例的判定。
(1)
50÷(5-0)
=50÷5
=10(立方米/分钟)
这个进水管每分钟进水量是10立方米。
(2)
由图象可以发现,进水量除以时间是一个定值,符合正比例的判定;这个进水管的进水量与时间成正比例关系。
【点睛】本题属于辨识两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
10. 80 25
【分析】从图中可以看出总价和买的长度成正比例关系,8元对应的是1米,所以每米需要8元,那么10米就需要(8×10)元,200可以买(200÷8)米。
【详解】8×10=80(元)
200÷8=25(米)
所以买10米这种彩带要花80元,200元可以买25米。
【点睛】此题考查了学生对正比例关系的辨识及应用。
11.×
【分析】根据正比例的意义进行解答,成正比例的两个量中,相对应的两个数的比值是一定的。
【详解】成正比例的两个量,它们的积是一定的。原题说法错误。
故答案为:×
【点睛】此题考查了正比例的意义。要求熟练掌握并灵活运用。
12.×
【分析】根据互相咬合齿轮的转数与齿轮的齿数成反比,即可得出答案。
【详解】因为互相咬合齿轮的转数与齿轮的齿数成反比,所以齿数比是5∶6,则它们的转数之比是6∶5。
故答案为:×
【点睛】解答本题要掌握:齿轮的齿数×转数=转过的总齿数(一定),所以齿轮的转数与齿数成反比例。
13.√
【分析】根据公式:总价÷订阅份数=单价,由于每本《悦读悦享》的价格是固定的,所以单价一定;当两个相关联的量的比值一定,则成正比例关系,据此即可判断。
【详解】由分析可知:
总价÷订阅份数=单价(一定),则订阅《悦读悦享》的总价和订阅份数成正式例。原题说法正确。
故答案为:√
【点睛】本题主要考查正比例的判定方法,熟练掌握它的意义是解题的关键。
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量之间对应的比值一定,还是乘积一定,如果比值一定,就成正比例,如果乘积一定,则成反比例,据此解答。
【详解】3x=5y,所以x∶y=5∶3=(一定),x和y成正比例。
x和y是两种相关联的量,如果3x=5y,那么x和y成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨别,反比例意义和辨别是解答本题的关键。
15.×
【分析】首先根据速度×时间=路程,可得路程一定时,时间和速度成反比,据此求出去时和返回用的时间的比是多少;然后根据路程÷时间=速度,用往返的路程除以往返用的总时间,求出她往返的平均速度是每分钟走多少米即可。
【详解】乐乐去时和返回用的时间的比是:50∶60=5∶6,
设去时用的时间是5t,则返回用的时间是6t,
(60×5t×2)÷(5t+6t)
=600t÷11t
=600÷11
=54(米/分)
故答案为:×
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
16.C
【分析】根据题意可知,路程÷时间=速度(一定),则路程和时间的比值一定,它们成正比例关系,据此设从甲城到乙城有420千米,x小时可以到达,列比例为420∶x=320∶4,然后解出比例即可;先用320÷4求出火车的速度,如果火车速度提高5%,则把原来火车的速度看作单位“1”,现在火车的速度是原来的(1+5%),根据百分数乘法的意义,用原来的速度乘(1+5%)即可求出现在的速度,然后用420千米除以现在火车的速度,即可求出如果火车速度提高5%,几小时就可以到达。
【详解】解:设从甲城到乙城有420千米,x小时可以到达。
420∶x=320∶4
320x=420×4
320x=1680
x=1680÷320
x=5.25
320÷4=80(千米/小时)
80×(1+5%)
=80×1.05
=84(千米/小时)
420÷84=5(小时)
从甲城到乙城有420千米,5.25小时可以到达;如果火车速度提高5%,5小时就可以到达。
故答案为:C
【点睛】本题主要考查了正比例的应用,掌握速度、时间、路程三者之间的关系是解答本题的关键。
17.D
【分析】根据统计图可知,在10分钟的时候,斑马跑了12千米,A选项据此判断;
长颈鹿的奔跑的路程和时间的商一定,也就是速度一定,可以判断长颈鹿奔跑的路程与时间是否成正比例,B选项据此解答;
根据速度=路程÷时间,先计算出长颈鹿的速度,再根据路程=速度×时间,求出长颈鹿50分钟跑的路程,C选项据此判断;
计算出斑马和长颈鹿的速度,再进行比较,即可判断谁跑的快,谁慢,D选项据此解答。
【详解】A.观察统计图可知,斑马跑12千米用了10分钟,原题干说法正确;
B.观察图形可知,长颈鹿奔跑的速度不变,根据路程÷时间=速度(一定),长颈鹿奔跑的路程与时间成正比例,原题干说法正确;
C.20÷25×50
=0.8×50
=40(千米)
照这样的速度长颈鹿跑40千米需50分钟,原题干说法正确;
D.斑马速度:24÷20=1.2(千米)
长颈鹿速度:20÷25=0.8(千米)
1.2千米>0.8千米,长颈鹿跑得慢。
原题干说法错误。
下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是斑马比长颈鹿跑得慢。
故答案为:D
【点睛】本题考查了对成正比例关系图像的认识,根据图像,按要求找出有用的信息进行计算解答本题。
18.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
①根据分数乘法的意义,可知甲数×=乙数×;再根据比例的基本性质:两外项之积等于两内项之积,可知甲数∶乙数=∶,求比值用比的前项除以后项即可;据此可知甲数和乙数的比值一定,则它们成正比例;
②根据比各部分的关系,可知比的后项×比值=比的前项(一定),比的后项和比值的乘积一定,则它们成反比例;
③圆柱的体积公式:S=πr2h,体积一定,底面半径的平方和高的乘积一定,则它们成反比例,但是底面半径和高不成比例;
④根据比和分数的关系,可知x∶2=3∶y,再根据比例的基本性质,可知xy=2×3,x和y的乘积一定,则它们成反比例。
【详解】①甲数的相当于乙数的,甲数和乙数成正比例;
②比的前项一定,比的后项和比值成反比例;
③圆柱的体积一定,它的底面半径和高不成比例;
④已知x、y是大于零的自然数,若,则x和y成反比例。
两个量成反比例关系的有2个,也就是②④。
故答案为:B
【点睛】本题考查了正比例、反比例的意义和辨识,掌握相关判别方法是解答本题的关键。
19.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。据此解答。
【详解】A.男运动员人数+女运动员人数=运动员总人数,参加冬奥会的男运动员人数与女运动员人数的和一定,不成比例;
B.已建场馆数+未建场馆数=冬奥会场馆总数,冬奥会已建场馆数与未建场馆数的和一定,不成比例;
C.速度×时间=路程,北京到崇礼区的路程一定,则高铁列车行驶的速度与时间的积一定,但是比值或商一定,那么行驶的速度与时间不成正比例关系;
D.接送运动员的总人数÷大巴车的数量=每辆大巴车的载客量(一定),则接送运动员的总人数与大巴车数量的商一定,则接送运动员的总人数与大巴车的数量成正比例关系。
故答案为:D
20.A
【分析】只有1和它本身两个因数的数叫做质数;一个数如果除了1和它本身还有别的因数,这样的数叫做合数;整数中,不是2的倍数的数叫做奇数。
分数的基本性质:分子和分母同时乘(或除以)同一个数(0除外),分数大小不变。
圆的周长.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就成反比例关系。
【详解】①×,,6是偶数不是奇数。
②×,分数的分子和分母同时乘或除以同一个数(0除外),分数大小不变。
③×,,周长一定,半径和圆周率都不变,不成比例。
所以说法正确的个数为0个。
故答案为:A
【点睛】考查了质数、合数、奇数的含义;分数的基本性质以及圆的周长公式、反比例的辨别,熟练掌握基础知识是关键。
21.见详解
【分析】根据表格中时间和路程的对应关系,找出相应的点,然后把它们按顺序连起来即可。
【详解】画图如下:
【点睛】此题考查了正比例的意义,即相关联的两种量,如果它们的比值一定,那么这两种量成正比例关系。
22.(1)18把
(2)6只
【分析】(1)由题可知:羊和斧头成正比例关系,设12只羊可以换x把斧头,4与6的比等于12与x的比,据此解答。
(2)设要换9把斧头,需要x只羊,4与6的比等于x与9的比,据此解答。
【详解】(1)解:设12只羊可以换x把斧头。
4∶6=12∶x
4x=6×12
4x=72
4x÷4=72÷4
x=18
答:12只羊可以换18把斧头。
(2)解:设要换9把斧头,需要x只羊。
4∶6=x∶9
6x=4×9
6x=36
x=6
答:需要6只羊。
【点睛】本题主要考查正比例的应用,同时要熟练掌握解比例的方法。
23.(1)该工厂每天生产的零件个数与需要的天数成反比例关系,理由如下:
因为200×36=300×24=400×18=600×12=7200,即每天生产的零件个数×需要的天数=零件总个数(一定),所以每天生产的辆数和所需的天数成反比例关系。
(2)800个
【分析】(1)根据表中数据求出每天生产的零件个数和所需的天数的乘积,再进一步判断即可。
(2)求平均每天要生产多少个零件,用总零件个数(200×36)除以时间9天即可。
【详解】(1)该工厂每天生产的零件个数与需要的天数成反比例关系,理由如下:
因为200×36=300×24=400×18=600×12=7200,即每天生产的零件个数×需要的天数=零件总个数(一定),所以每天生产的辆数和所需的天数成反比例关系。
(2)200×36÷9
=7200÷9
=800(个)
答:平均每天要生产800个零件。
【点睛】此题属于辨识成正、反比例的量以及利用反比例的意义解决实际问题。
24.960个
【分析】设1台智能机器人12小时能处理x份订单,工作效率一定,工作总量和工作时间成正比例,据此列比例解答即可。
【详解】30分钟小时
解:设1台智能机器人12小时能处理x个订单。
0.5x=40×12
0.5x=480
0.5x÷0.5=480÷0.5
答:1台智能机器人12小时能处理960个订单。
25.①见详解
②见详解
③正
【分析】①根据“路程=速度×时间”,代入数据求出路程即可;
②在图中描出各点,再连线即可;
③两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例;时间与路程的比值一定,可知时间与路程成正比例。
【详解】①
60×2=120(千米)
60×3=180(千米)
60×4=240(千米)
60×5=300(千米)
60×6=360(千米)
时间/时 1 2 3 4 5 6 …
路程/km 60 120 180 240 300 360 …
②
③1÷60=2÷120=3÷180=4÷240=5÷300=6÷360=(一定),时间与路程成正比例。
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
26.(1)见详解
(2)见详解
(3)30;19
【分析】(1)如果两个相关联的量的比值一定,那么这两个相关联的量成正比例关系,据此解答即可;
(2)将应付金额和长度对应的点描在方格纸上,再顺次连接即可;
(3)根据1米丝带的价格是4元,用单价×数量=总价,可求出购买7.5米丝带需要多少元;用总价÷单价=数量,可求得76元最多可以购买多长的丝带。
【详解】(1)应付金额与长度成正比例关系。
因为(一定),所以应付金额与长度成正比例关系。
(2)
(3)(元)
(米)
购买7.5米丝带需要30元;76元最多可以购买19长的丝带。
【点睛】熟练掌握正比例关系的定义,是解答此题的关键。
27.(1)48万;64万;80万;
(2)正比例;理由见详解
(3)见详解;
(4)56万立方米;2.5天
【分析】(1)根据喷水天数与喷水量之间的观察完成表格;
(2)计算出表格中喷水量与喷水天数的比值,看比值是否相等;
(3)根据表格中的数据在图中描点、连线。
(4)结合图像进行计算。
【详解】(1)
喷水天数/天 0 1 2 3 4 5
喷水量/m3 0 16万 32万 48万 64万 80万
(2)16÷1=32÷2=48÷3=64÷4=80÷5=16(一定)
因为喷水量和喷水天数的比值一定,所以喷水量与喷水天数成正比例;
(3)
(4)3.5×16=56(万立方米)
40÷16=2.5(天)
3.5天的喷水量是56万立方米;40万立方米的喷水量需要喷2.5天。
【点睛】本题考查了成正比例关系的判定、统计表及统计图的填补、从统计表或统计图中读出信息、分析数据、解决问题的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
