人教版六年级数学下册第四单元比例高频易错题检测卷一(含解析)
文档属性
| 名称 | 人教版六年级数学下册第四单元比例高频易错题检测卷一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 511.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 15:55:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版六年级数学下册第四单元比例高频易错题检测卷一
一、填空题(共20分)
1.(2分)从12的因数中选4个数组成一个比例,并写出来:( )。
2.(2分)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是( )。
3.(2分)甲,乙两种商品的价格比为6∶3,如果它们的价格分别下降12元,其价格比则变为8∶3,那么甲商品原价是( )元,乙商品原价是( )元。
4.(2分)亮亮把一个圆形铁片按照1∶2画在图纸上,直径是8厘米。圆形铁片的实际面积是( )平方厘米。
5.(2分)填表。
比例尺 图上距离 实际距离
1∶50000 ( )cm 3.2km
( ) 2.6cm 104km
6.(2分)一个半径是3厘米的圆,按2∶1放大,得到的图形的面积是( )平方厘米。
7.(2分)大小齿轮的齿数比是,大齿轮有35个齿,小齿轮有( )个齿。
8.(2分)《中华人民共和国国旗法》规定,我国国旗的长与宽之比为3∶2,有一面国旗的长是150cm,它的宽是( )cm。
9.(2分)如果(m、n都不为0),那么( ),m和n成( )比例。
10.(2分)为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
二、判断题(共10分)
11.(2分)比例尺的前项表示图上距离,它一定是1。( )
12.(2分)6.2∶3.1=2是一个比例。( )
13.(2分)如果图上距离1厘米表示实际距离200米,那么这幅图的比例尺是1∶200。( )
14.(2分)小敏每天步行上学,她的步行平均速度与上学路上所花时间成反比例。( )
15.(2分)在比例中,两个外项互为倒数,则两个内项也互为倒数。( )
三、选择题(共10分)
16.(2分)盒子里有黑、白两种棋子,先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5。如果放入的黑棋子和白棋子的数量比是3∶7,那么原来盒子中黑、白棋子的数量之比是( )。
A.6∶5 B.5∶6 C.4∶3 D.3∶4
17.(2分)一张图纸上,用1cm的线段表示实际长1mm,这张图纸的比例尺是( )。
A.1∶10 B.1∶100 C.100∶1 D.10∶1
18.(2分)下面表示a和b成正比例关系的式子是( )。
A.ab=6;6b=a B.6÷a=b;6a=b C.6a=b;6b=a D.6b=a;6÷a=b
19.(2分)下列说法中,正确的是( )。
①2022年是平年,全年共有365天
②圆的面积和圆的半径成正比例
③1m的与5m的同样长
④一个质数加上1,所得的和一定是合数
A.①② B.②③ C.③④ D.①③
20.(2分)小强和小华分别画出学校花坛的平面图(如图)。小强是按1∶50的比例尺画的,那么小华是按( )的比例尺画的。
A.1∶2 B.1∶10 C.1∶25 D.1∶100
四、计算题(共6分)
21.(6分)解比例。
五、作图题(共6分)
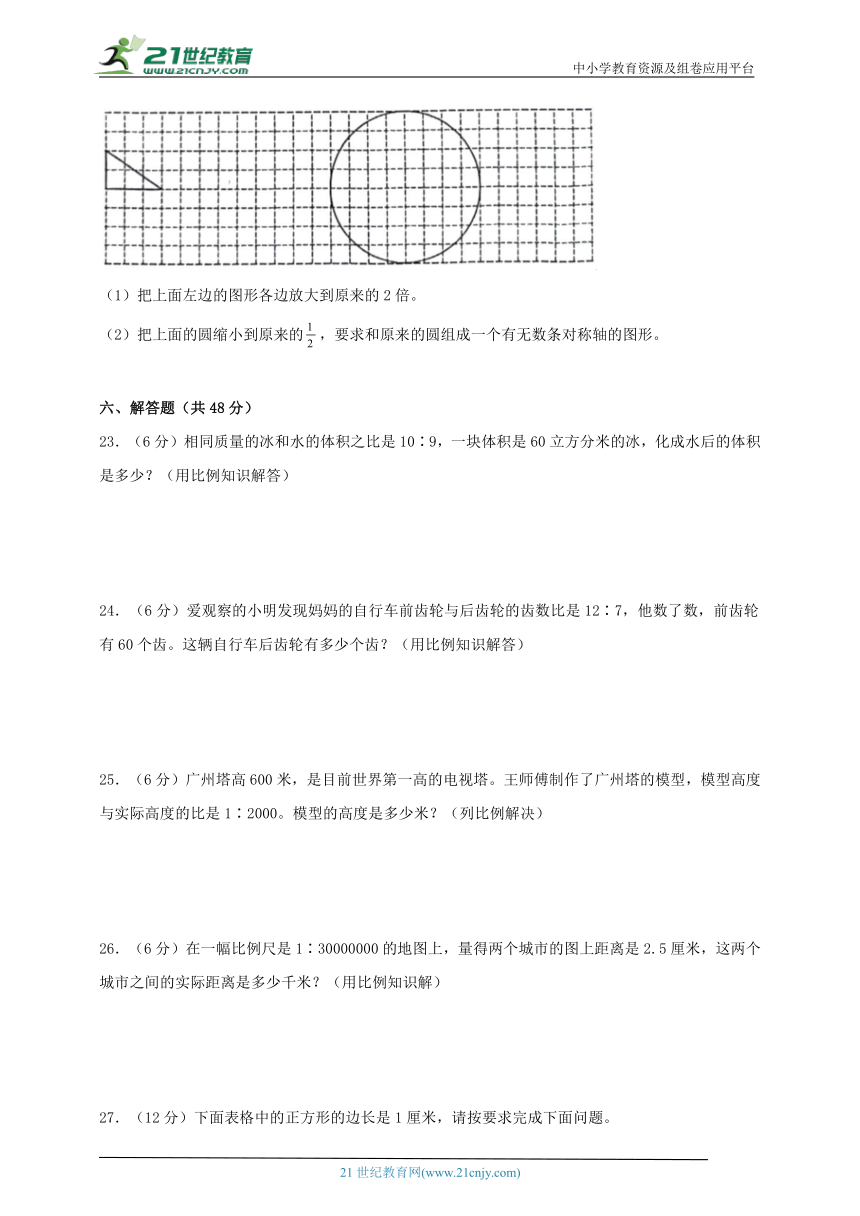
22.(6分)在方格纸上按要求画图。
(1)把上面左边的图形各边放大到原来的2倍。
(2)把上面的圆缩小到原来的,要求和原来的圆组成一个有无数条对称轴的图形。
六、解答题(共48分)
23.(6分)相同质量的冰和水的体积之比是10∶9,一块体积是60立方分米的冰,化成水后的体积是多少?(用比例知识解答)
24.(6分)爱观察的小明发现妈妈的自行车前齿轮与后齿轮的齿数比是12∶7,他数了数,前齿轮有60个齿。这辆自行车后齿轮有多少个齿?(用比例知识解答)
25.(6分)广州塔高600米,是目前世界第一高的电视塔。王师傅制作了广州塔的模型,模型高度与实际高度的比是1∶2000。模型的高度是多少米?(列比例解决)
26.(6分)在一幅比例尺是1∶30000000的地图上,量得两个城市的图上距离是2.5厘米,这两个城市之间的实际距离是多少千米?(用比例知识解)
27.(12分)下面表格中的正方形的边长是1厘米,请按要求完成下面问题。
(1)在方格纸中作一个长为3厘米、宽为2厘米的长方形。
(2)画出上面图形按2∶1放大的图形。
(3)原图的面积是( )平方厘米,放大后的图形的面积是( )平方厘米。
(4)观察上面的数据,可以看出把图形放大到原来的n倍,则周长扩大到原来的( )倍,面积扩大到原来的( )倍。
28.(12分)给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积/平方米 0.1 0.2 0.3 0.5 0.6 …
所需地砖的数量/块 300 150 100 60 50 …
(1)每块地砖的面积和所需地砖的数量有什么关系?
(2)如果每块地砖的面积是0.4平方米,铺这一地面需要多少块地砖?
(3)铺这一地面用了200块地砖,所用的地砖每块面积是多大?
参考答案
1.1∶2=6∶12
【分析】列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
表示两个比相等的式子叫做比例。
先列举出12所有的因数,再根据比例的意义,找出比值相等的两个比组成比例即可。
【详解】12的因数:1,2,3,4,6,12;
1∶2=1÷2=
6∶12=6÷12=
1∶2和6∶12的比值相等,可以组成一个比例:
1∶2=6∶12
(答案不唯一)
【点睛】本题考查找一个数的因数的方法、比例的意义及应用。
2.2.5/
【分析】根据比例的性质“在比例里,两个外项的积等于两个内项的积”,根据倒数的意义,两个外项互为倒数即两外项的乘积是1,故两内向的乘积也是1,据此可计算出另一个内项。
【详解】由分析可知,0.4乘另一个内项等于1,求另一个内项;
1÷0.4=2.5
所以另一个内项是2.5。
3. 60 30
【分析】由题意可得:设这两种商品的价格原来分别是6x和3x,则后来的价格分别为(6x-12)和(3x-12),再据后来的价格比为8∶3,即可列比例求解。
【详解】解:设甲商品原价是6x元,乙商品的原价为3x元。
(6x-12)∶(3x-12)=8∶3
(3x-12)×8=(6x-12)×3
24x-96=18x-36
24x-96+96=18x-36+96
24x=18x+60
24x-18x =18x+60-18x
6x=60
6x÷6=60÷6
x=10
10×6=60(元)
10×3=30(元)
则甲商品原价是60元,乙商品原价是30元。
【点睛】解答此题的关键是弄清楚原来的价格和现在的价格的比,列比例求解即可。
4.200.96
【分析】要求圆形铁片的实际面积,根据“图上距离÷比例尺=实际距离”,求出实际直径的长;然后根据圆的面积=πr2计算出实际面积即可。
【详解】8÷
=8×2
=16(厘米)
3.14×(16÷2)2
=3.14×82
=3.14×64
=200.96(平方厘米)
圆形铁片的实际面积是200.96平方厘米。
5.6.4;1∶4000000
【分析】根据比例尺=图上距离∶实际距离,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,代入数据解答即可。
【详解】3.2km=320000cm
320000×=6.4(cm)
2.6cm∶104km
=2.6cm∶10400000cm
=(2.6×10÷26)∶(10400000×10÷26)
=1∶4000000
比例尺 图上距离 实际距离
1∶50000 6.4cm 3.2km
1∶4000000 2.6cm 104km
6.113.04
【分析】一个半径是3厘米的圆,按2∶1放大,则此时的半径为3×2=6厘米,再根据圆的面积公式:S=πr2,据此进行计算即可。
【详解】3×2=6(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
则得到的图形的面积是113.04平方厘米。
【点睛】本题考查图形的放大,结合圆的面积的计算方法是解题的关键。
7.20
【分析】设小齿轮有x个齿,根据大齿轮齿数∶小齿轮齿数=7∶4,列出比例解答即可。
【详解】解:设小齿轮有x个齿。
35∶x=7∶4
7x=35×4
7x=140
7x÷7=140÷7
x=20
小齿轮有20个齿。
【点睛】用比例解决问题只要比例两边的比统一即可。
8.100
【分析】由题意可知,我国国旗的长与宽之比为3∶2,有一面国旗的长是150cm,设它的宽是xcm,据此列比例解答即可。
【详解】解:设它的宽是xcm。
150∶x=3∶2
3x=150×2
3x=300
3x÷3=300÷3
x=100
则它的宽是100cm。
【点睛】本题考查比例的应用,明确等量关系是解题的关键。
9. 正
【分析】根据题意,可先将改写成7m=5n,然后等式两边同时除以7,除以n,即可通过转化得出m和n的比。或根据比例的基本性质直接得到。根据x÷y=k(一定),x和y成正比例关系,即可确定m和n的比例关系。
【详解】由可得7m=5n
7m÷7÷n=5n÷7÷n
m÷n=5÷7=
所以,m∶n=5∶7,m和n成正比例关系。
10.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
11.×
【详解】比例尺是表示图上一条线段的长度与实际长度之比。比例尺的前项表示图上距离,缩小比例尺的前项一般是1,而扩大比例尺的后项一般是1,例如比例尺20∶1的前项不一定是1,所以原题说法错误。
故答案为:×
12.×
【分析】比值相等的两个比,可以组成比例。据此判断。
【详解】6.2∶3.1是一个比,2是一个值,6.2∶3.1=2不是一个比例。6.2∶3.1=2∶1是一个比例。
故答案为:×
13.×
【分析】根据“比例尺=图上距离∶实际距离”以及进率“1米=100厘米”,即可求出这幅图的比例尺。
【详解】1厘米∶200米
=1厘米∶(200×100)厘米
=1∶20000
这幅图的比例尺是1∶20000。
原题说法错误。
故答案为:×
14.√
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】步行的平均速度×上学路上所花时间=上学的路程(一定)
乘积一定,则她的步行平均速度与上学路上所花时间成反比例。
原题说法正确。
故答案为:√
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
15.√
【分析】根据比例的基本性质,内项积等于外项积;互为倒数的两个数的乘积为1,据此判断即可。
【详解】由分析可知:
在比例中,两个外项互为倒数,则两个内项也互为倒数。原题干说法正确。
故答案为:√
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
16.D
【分析】设原来有黑棋子x个,白棋子y个。先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,黑棋子没有发生改变,则现在的白棋子是黑棋子的,则白棋子有个,则放进白棋子的的数量=现在白棋子的数量-原来白棋子的数量=个。然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5,白棋子的数量没有发生改变,现在黑棋子的数量是白棋子的,则现在黑棋子的数量为个,那么放进去的黑棋子的数量=现在黑棋子的数量-原来黑棋子的数量=个。根据放入的黑棋子和白棋子的数量比是3∶7列出比例,再根据比例的基本性质化简比例得出,根据比例的基本性子,x∶y=3∶4。
【详解】设:原来有黑棋子x个,白棋子y个。
x∶y=3∶4
原来盒子中黑、白棋子的数量之比是3∶4
故答案为:D
17.D
【分析】根据图上距离∶实际距离=比例尺,据此进行计算即可。
【详解】1cm∶1mm
=10mm∶1mm
=10∶1
这张图纸的比例尺是10∶1。
故答案为:D
18.C
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】A.ab=6,积一定,则a和b成反比例关系;不符合题意;
B.6÷a=b,即ab=6,积一定,则a和b成反比例关系;不符合题意;
C.6a=b,即b÷a=6,商一定,则a和b成正比例关系;
6b=a,则a÷b=6,商一定,则a和b成正比例关系,符合题意;
D.6b=a,即a÷b=6,商一定,则a和b成正比例关系;
6÷a=b,即ab=6,积一定,则a和b成反比例关系;不符合题意。
故答案为:C
19.D
【分析】①平年一年有365天,闰年一年有366天,再结合公历年份是4的倍数的一般都是闰年,但年份是100的倍数时,必须是400的倍数才是闰年,据此判断即可;
②两个相关联的量,若它们的比值一定,则它们成正比例,据此判断即可;
③根据求一个数的几分之几是多少,用乘法计算,据此分别求出1m的与5m的,再进行对比即可;
④一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数;据此举例判断即可。
【详解】①2022÷4=505 2
则2022年是平年,全年共有365天,原说法正确;
②由S=πr2可知,S∶r2=π(一定),比值一定,圆的面积与半径的平方成正比例;原说法错误;
③1×=(m)
5×=(m)
则1m的与5m的同样长,原说法正确;
④如:质数2,2+1=3,3不是合数,所以原说法错误。
则正确的是①③。
故答案为:D
20.C
【分析】小强是按1∶50的比例尺画的,1∶50表示图上1厘米代表实际距离50厘米,小强画的一条边的图上距离是5厘米,用50乘5即可求出花坛这条边的实际长度。图上距离∶实际距离=比例尺,据此用10比上求出的这条边的实际长度,即可求出小华的比例尺。
【详解】50×5=250(厘米)
10∶250=1∶25
则小华是按1∶25的比例尺画的。
故答案为:C
21.x=0.6;x=20;x=130
【分析】(1)根据比例的基本性质,把比例式化为乘积式4x=0.8×3,再根据等式的性质,在方程两边同时除以4即可;
(2)根据比例的基本性质,把比例式化为乘积式2x=25×1.6,再根据等式的性质,在方程两边同时除以2即可;
(3)根据比例的基本性质,把比例式化为乘积式,再根据等式的性质,在方程两边同时除以即可。
【详解】
解:4x=0.8×3
4x=2.4
4x÷4=2.4÷4
x=0.6
解:2x=25×1.6
2x=40
2x÷2=40÷2
x=20
解:
x=130
22.见详解
【分析】(1)图中三角形的底是3,高是2,把它的各边放大到原来的2倍,则原来三角形的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
(2)图中圆的半径是4,把它缩小到原来的,则原来圆的半径除以2,即是缩小后圆的半径。
要求和原来的圆组成一个有无数条对称轴的图形,根据轴对称图形的意义,缩小后的圆与原来的圆必须是同心圆,据此画出缩小后的圆。
一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】(1)放大后的三角形的底:3×2=6
放大后的三角形的高:2×2=4
画一个底是6,高是4的三角形,如下图。
(2)缩小后圆的半径:8÷2=4
画一个半径为4的同心圆,即可和原来的圆组成一个有无数条对称轴的图形。
如图:
【点睛】本题考查作放大和缩小后图形的作图方法以及轴对称图形,明确放大或缩小图形,只改变图形的大小,不改变图形的形状。
23.54立方分米
【分析】根据题意,冰和水的体积之比是10∶9,即它们的体积比值不变,设体积是60立方分米的冰,化成水后的体积是x立方分米,列比例:10∶9=60∶x,解比例,即可解答。
【详解】设化成水后的体积是x立方分米。
10∶9=60∶x
10x=9×60
10x=540
x=540÷10
x=54
答:化成水后的体积是54立方分米。
【点睛】本题主要考查根据比例的基本性质列出比例,再进行解比例的能力。
24.35个
【分析】根据题意可知“前齿轮的齿数∶后齿轮的齿数=12∶7”,已知前齿轮有60个齿,如果设这辆自行车后齿轮有x个齿,则可以列出比例60∶x=12∶7。再根据比例的基本性质解比例即可。
【详解】解:设这辆自行车后齿轮有x个齿。
60∶x=12∶7
12x=60×7
x=
x=35
答:这辆自行车后齿轮有35个齿。
【点睛】此题考查了运用比例的知识解决问题。解决此题的关键是理解比例的意义、解比例的意义及掌握解比例的方法。
25.0.3米
【分析】由题意可知,设模型的高度是x米,再根据模型的高度与实际的高度比是1∶2000,列出比例解比例即可。
【详解】解:设模型的高度是x米。
x∶600=1∶2000
2000x=600×1
2000x=600
2000x÷2000=600÷2000
x=0.3
答:模型的高度是0.3米。
26.
750千米
【分析】已知一幅地图的比例尺和两个城市的图上距离,可根据图上距离∶实际距离=比例尺,列出比例方程解答即可。
【详解】解:设两个城市之间的实际距离是x厘米。
1∶30000000=2.5∶x
x=75000000
75000000厘米=750千米
答:这两个城市之间的实际距离是750千米。
【点睛】本题考查列比例方程解答问题,解答本题的关键是掌握列比例方程解答问题的方法。
27.(1)见详解
(2)见详解
(3)6;24
(4)n;n2
【分析】(1)根据长方形的特征,画出一个长为3厘米、宽为2厘米的长方形。
(2)长方形按2∶1放大,原来长方形的长和宽都乘2,即是放大后长方形的长和宽,据此画出放大后的长方形。
(3)根据长方形的面积=长×宽,分别求出原长方形和放大后的长方形的面积。
(4)长方形按2∶1放大,那么长方形的每一条边都扩大到原来的2倍;
原来长方形的周长是10厘米,放大后长方形的周长是20厘米,周长扩大到原来的2倍;
原来长方形的面积是6平方厘米,放大后长方形的面积是24平方厘米,面积扩大到原来的4倍;据此得出规律。
【详解】(1)长为3厘米、宽为2厘米的长方形如下图。
(2)放大后长方形的长是:3×2=6(厘米)
放大后长方形的宽是:2×2=4(厘米)
放大后的长方形如下图。
(3)原长方形的面积:3×2=6(平方厘米)
放大后长方形的面积:6×4=24(平方厘米)
原图的面积是6平方厘米,放大后的图形的面积是24平方厘米。
(4)观察上面的数据,可以看出把图形放大到原来的n倍,则周长扩大到原来的n倍,面积扩大到原来的n2倍。
【点睛】本题考查长方形的画法、作放大后的图形、长方形面积公式的运用以及图形放大后,图形的周长、面积的变化规律。
28.(1)反比例;(2)75块;(3)0.15平方米
【分析】(1)根据题意可知,每块地砖的面积×所需地砖的数量=总面积(一定),每块地砖的面积和所需地砖的数量的乘积一定,则它们成反比例关系;
(2)根据总面积÷每块地砖的面积=所需地砖的数量,用总面积除以0.4平方米,即可求出所需地砖的块数;
(3)根据总面积÷所需地砖的数量=每块地砖的面积,用总面积除以200块,即可求出每块地砖的面积。
【详解】(1)0.1×300=30(平方米)
0.2×150=30(平方米)
0.3×100=30(平方米)
0.5×60=30(平方米)
0.6×50=30(平方米)
每块地砖的面积和所需地砖的数量的乘积一定,则它们成反比例关系;
(2)30÷0.4=75(块)
答:如果每块地砖的面积是0.4平方米,铺这一地面需要75块地砖。
(3)300÷200=1.5(平方米)
答:铺这一地面用了200块地砖,所用的地砖每块面积是1.5平方米。
【点睛】本题考查了反比例的意义和应用,判断相关量是正比例还是反比例是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级数学下册第四单元比例高频易错题检测卷一
一、填空题(共20分)
1.(2分)从12的因数中选4个数组成一个比例,并写出来:( )。
2.(2分)一个比例的两个外项互为倒数,如果其中一个内项为0.4,另一个内项是( )。
3.(2分)甲,乙两种商品的价格比为6∶3,如果它们的价格分别下降12元,其价格比则变为8∶3,那么甲商品原价是( )元,乙商品原价是( )元。
4.(2分)亮亮把一个圆形铁片按照1∶2画在图纸上,直径是8厘米。圆形铁片的实际面积是( )平方厘米。
5.(2分)填表。
比例尺 图上距离 实际距离
1∶50000 ( )cm 3.2km
( ) 2.6cm 104km
6.(2分)一个半径是3厘米的圆,按2∶1放大,得到的图形的面积是( )平方厘米。
7.(2分)大小齿轮的齿数比是,大齿轮有35个齿,小齿轮有( )个齿。
8.(2分)《中华人民共和国国旗法》规定,我国国旗的长与宽之比为3∶2,有一面国旗的长是150cm,它的宽是( )cm。
9.(2分)如果(m、n都不为0),那么( ),m和n成( )比例。
10.(2分)为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
二、判断题(共10分)
11.(2分)比例尺的前项表示图上距离,它一定是1。( )
12.(2分)6.2∶3.1=2是一个比例。( )
13.(2分)如果图上距离1厘米表示实际距离200米,那么这幅图的比例尺是1∶200。( )
14.(2分)小敏每天步行上学,她的步行平均速度与上学路上所花时间成反比例。( )
15.(2分)在比例中,两个外项互为倒数,则两个内项也互为倒数。( )
三、选择题(共10分)
16.(2分)盒子里有黑、白两种棋子,先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5。如果放入的黑棋子和白棋子的数量比是3∶7,那么原来盒子中黑、白棋子的数量之比是( )。
A.6∶5 B.5∶6 C.4∶3 D.3∶4
17.(2分)一张图纸上,用1cm的线段表示实际长1mm,这张图纸的比例尺是( )。
A.1∶10 B.1∶100 C.100∶1 D.10∶1
18.(2分)下面表示a和b成正比例关系的式子是( )。
A.ab=6;6b=a B.6÷a=b;6a=b C.6a=b;6b=a D.6b=a;6÷a=b
19.(2分)下列说法中,正确的是( )。
①2022年是平年,全年共有365天
②圆的面积和圆的半径成正比例
③1m的与5m的同样长
④一个质数加上1,所得的和一定是合数
A.①② B.②③ C.③④ D.①③
20.(2分)小强和小华分别画出学校花坛的平面图(如图)。小强是按1∶50的比例尺画的,那么小华是按( )的比例尺画的。
A.1∶2 B.1∶10 C.1∶25 D.1∶100
四、计算题(共6分)
21.(6分)解比例。
五、作图题(共6分)
22.(6分)在方格纸上按要求画图。
(1)把上面左边的图形各边放大到原来的2倍。
(2)把上面的圆缩小到原来的,要求和原来的圆组成一个有无数条对称轴的图形。
六、解答题(共48分)
23.(6分)相同质量的冰和水的体积之比是10∶9,一块体积是60立方分米的冰,化成水后的体积是多少?(用比例知识解答)
24.(6分)爱观察的小明发现妈妈的自行车前齿轮与后齿轮的齿数比是12∶7,他数了数,前齿轮有60个齿。这辆自行车后齿轮有多少个齿?(用比例知识解答)
25.(6分)广州塔高600米,是目前世界第一高的电视塔。王师傅制作了广州塔的模型,模型高度与实际高度的比是1∶2000。模型的高度是多少米?(列比例解决)
26.(6分)在一幅比例尺是1∶30000000的地图上,量得两个城市的图上距离是2.5厘米,这两个城市之间的实际距离是多少千米?(用比例知识解)
27.(12分)下面表格中的正方形的边长是1厘米,请按要求完成下面问题。
(1)在方格纸中作一个长为3厘米、宽为2厘米的长方形。
(2)画出上面图形按2∶1放大的图形。
(3)原图的面积是( )平方厘米,放大后的图形的面积是( )平方厘米。
(4)观察上面的数据,可以看出把图形放大到原来的n倍,则周长扩大到原来的( )倍,面积扩大到原来的( )倍。
28.(12分)给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积/平方米 0.1 0.2 0.3 0.5 0.6 …
所需地砖的数量/块 300 150 100 60 50 …
(1)每块地砖的面积和所需地砖的数量有什么关系?
(2)如果每块地砖的面积是0.4平方米,铺这一地面需要多少块地砖?
(3)铺这一地面用了200块地砖,所用的地砖每块面积是多大?
参考答案
1.1∶2=6∶12
【分析】列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
表示两个比相等的式子叫做比例。
先列举出12所有的因数,再根据比例的意义,找出比值相等的两个比组成比例即可。
【详解】12的因数:1,2,3,4,6,12;
1∶2=1÷2=
6∶12=6÷12=
1∶2和6∶12的比值相等,可以组成一个比例:
1∶2=6∶12
(答案不唯一)
【点睛】本题考查找一个数的因数的方法、比例的意义及应用。
2.2.5/
【分析】根据比例的性质“在比例里,两个外项的积等于两个内项的积”,根据倒数的意义,两个外项互为倒数即两外项的乘积是1,故两内向的乘积也是1,据此可计算出另一个内项。
【详解】由分析可知,0.4乘另一个内项等于1,求另一个内项;
1÷0.4=2.5
所以另一个内项是2.5。
3. 60 30
【分析】由题意可得:设这两种商品的价格原来分别是6x和3x,则后来的价格分别为(6x-12)和(3x-12),再据后来的价格比为8∶3,即可列比例求解。
【详解】解:设甲商品原价是6x元,乙商品的原价为3x元。
(6x-12)∶(3x-12)=8∶3
(3x-12)×8=(6x-12)×3
24x-96=18x-36
24x-96+96=18x-36+96
24x=18x+60
24x-18x =18x+60-18x
6x=60
6x÷6=60÷6
x=10
10×6=60(元)
10×3=30(元)
则甲商品原价是60元,乙商品原价是30元。
【点睛】解答此题的关键是弄清楚原来的价格和现在的价格的比,列比例求解即可。
4.200.96
【分析】要求圆形铁片的实际面积,根据“图上距离÷比例尺=实际距离”,求出实际直径的长;然后根据圆的面积=πr2计算出实际面积即可。
【详解】8÷
=8×2
=16(厘米)
3.14×(16÷2)2
=3.14×82
=3.14×64
=200.96(平方厘米)
圆形铁片的实际面积是200.96平方厘米。
5.6.4;1∶4000000
【分析】根据比例尺=图上距离∶实际距离,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,代入数据解答即可。
【详解】3.2km=320000cm
320000×=6.4(cm)
2.6cm∶104km
=2.6cm∶10400000cm
=(2.6×10÷26)∶(10400000×10÷26)
=1∶4000000
比例尺 图上距离 实际距离
1∶50000 6.4cm 3.2km
1∶4000000 2.6cm 104km
6.113.04
【分析】一个半径是3厘米的圆,按2∶1放大,则此时的半径为3×2=6厘米,再根据圆的面积公式:S=πr2,据此进行计算即可。
【详解】3×2=6(厘米)
3.14×62
=3.14×36
=113.04(平方厘米)
则得到的图形的面积是113.04平方厘米。
【点睛】本题考查图形的放大,结合圆的面积的计算方法是解题的关键。
7.20
【分析】设小齿轮有x个齿,根据大齿轮齿数∶小齿轮齿数=7∶4,列出比例解答即可。
【详解】解:设小齿轮有x个齿。
35∶x=7∶4
7x=35×4
7x=140
7x÷7=140÷7
x=20
小齿轮有20个齿。
【点睛】用比例解决问题只要比例两边的比统一即可。
8.100
【分析】由题意可知,我国国旗的长与宽之比为3∶2,有一面国旗的长是150cm,设它的宽是xcm,据此列比例解答即可。
【详解】解:设它的宽是xcm。
150∶x=3∶2
3x=150×2
3x=300
3x÷3=300÷3
x=100
则它的宽是100cm。
【点睛】本题考查比例的应用,明确等量关系是解题的关键。
9. 正
【分析】根据题意,可先将改写成7m=5n,然后等式两边同时除以7,除以n,即可通过转化得出m和n的比。或根据比例的基本性质直接得到。根据x÷y=k(一定),x和y成正比例关系,即可确定m和n的比例关系。
【详解】由可得7m=5n
7m÷7÷n=5n÷7÷n
m÷n=5÷7=
所以,m∶n=5∶7,m和n成正比例关系。
10.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
11.×
【详解】比例尺是表示图上一条线段的长度与实际长度之比。比例尺的前项表示图上距离,缩小比例尺的前项一般是1,而扩大比例尺的后项一般是1,例如比例尺20∶1的前项不一定是1,所以原题说法错误。
故答案为:×
12.×
【分析】比值相等的两个比,可以组成比例。据此判断。
【详解】6.2∶3.1是一个比,2是一个值,6.2∶3.1=2不是一个比例。6.2∶3.1=2∶1是一个比例。
故答案为:×
13.×
【分析】根据“比例尺=图上距离∶实际距离”以及进率“1米=100厘米”,即可求出这幅图的比例尺。
【详解】1厘米∶200米
=1厘米∶(200×100)厘米
=1∶20000
这幅图的比例尺是1∶20000。
原题说法错误。
故答案为:×
14.√
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】步行的平均速度×上学路上所花时间=上学的路程(一定)
乘积一定,则她的步行平均速度与上学路上所花时间成反比例。
原题说法正确。
故答案为:√
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
15.√
【分析】根据比例的基本性质,内项积等于外项积;互为倒数的两个数的乘积为1,据此判断即可。
【详解】由分析可知:
在比例中,两个外项互为倒数,则两个内项也互为倒数。原题干说法正确。
故答案为:√
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
16.D
【分析】设原来有黑棋子x个,白棋子y个。先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,黑棋子没有发生改变,则现在的白棋子是黑棋子的,则白棋子有个,则放进白棋子的的数量=现在白棋子的数量-原来白棋子的数量=个。然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5,白棋子的数量没有发生改变,现在黑棋子的数量是白棋子的,则现在黑棋子的数量为个,那么放进去的黑棋子的数量=现在黑棋子的数量-原来黑棋子的数量=个。根据放入的黑棋子和白棋子的数量比是3∶7列出比例,再根据比例的基本性质化简比例得出,根据比例的基本性子,x∶y=3∶4。
【详解】设:原来有黑棋子x个,白棋子y个。
x∶y=3∶4
原来盒子中黑、白棋子的数量之比是3∶4
故答案为:D
17.D
【分析】根据图上距离∶实际距离=比例尺,据此进行计算即可。
【详解】1cm∶1mm
=10mm∶1mm
=10∶1
这张图纸的比例尺是10∶1。
故答案为:D
18.C
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】A.ab=6,积一定,则a和b成反比例关系;不符合题意;
B.6÷a=b,即ab=6,积一定,则a和b成反比例关系;不符合题意;
C.6a=b,即b÷a=6,商一定,则a和b成正比例关系;
6b=a,则a÷b=6,商一定,则a和b成正比例关系,符合题意;
D.6b=a,即a÷b=6,商一定,则a和b成正比例关系;
6÷a=b,即ab=6,积一定,则a和b成反比例关系;不符合题意。
故答案为:C
19.D
【分析】①平年一年有365天,闰年一年有366天,再结合公历年份是4的倍数的一般都是闰年,但年份是100的倍数时,必须是400的倍数才是闰年,据此判断即可;
②两个相关联的量,若它们的比值一定,则它们成正比例,据此判断即可;
③根据求一个数的几分之几是多少,用乘法计算,据此分别求出1m的与5m的,再进行对比即可;
④一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;一个自然数如果除了1和它本身还有其它的因数,那么这个自然数叫做合数;据此举例判断即可。
【详解】①2022÷4=505 2
则2022年是平年,全年共有365天,原说法正确;
②由S=πr2可知,S∶r2=π(一定),比值一定,圆的面积与半径的平方成正比例;原说法错误;
③1×=(m)
5×=(m)
则1m的与5m的同样长,原说法正确;
④如:质数2,2+1=3,3不是合数,所以原说法错误。
则正确的是①③。
故答案为:D
20.C
【分析】小强是按1∶50的比例尺画的,1∶50表示图上1厘米代表实际距离50厘米,小强画的一条边的图上距离是5厘米,用50乘5即可求出花坛这条边的实际长度。图上距离∶实际距离=比例尺,据此用10比上求出的这条边的实际长度,即可求出小华的比例尺。
【详解】50×5=250(厘米)
10∶250=1∶25
则小华是按1∶25的比例尺画的。
故答案为:C
21.x=0.6;x=20;x=130
【分析】(1)根据比例的基本性质,把比例式化为乘积式4x=0.8×3,再根据等式的性质,在方程两边同时除以4即可;
(2)根据比例的基本性质,把比例式化为乘积式2x=25×1.6,再根据等式的性质,在方程两边同时除以2即可;
(3)根据比例的基本性质,把比例式化为乘积式,再根据等式的性质,在方程两边同时除以即可。
【详解】
解:4x=0.8×3
4x=2.4
4x÷4=2.4÷4
x=0.6
解:2x=25×1.6
2x=40
2x÷2=40÷2
x=20
解:
x=130
22.见详解
【分析】(1)图中三角形的底是3,高是2,把它的各边放大到原来的2倍,则原来三角形的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
(2)图中圆的半径是4,把它缩小到原来的,则原来圆的半径除以2,即是缩小后圆的半径。
要求和原来的圆组成一个有无数条对称轴的图形,根据轴对称图形的意义,缩小后的圆与原来的圆必须是同心圆,据此画出缩小后的圆。
一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】(1)放大后的三角形的底:3×2=6
放大后的三角形的高:2×2=4
画一个底是6,高是4的三角形,如下图。
(2)缩小后圆的半径:8÷2=4
画一个半径为4的同心圆,即可和原来的圆组成一个有无数条对称轴的图形。
如图:
【点睛】本题考查作放大和缩小后图形的作图方法以及轴对称图形,明确放大或缩小图形,只改变图形的大小,不改变图形的形状。
23.54立方分米
【分析】根据题意,冰和水的体积之比是10∶9,即它们的体积比值不变,设体积是60立方分米的冰,化成水后的体积是x立方分米,列比例:10∶9=60∶x,解比例,即可解答。
【详解】设化成水后的体积是x立方分米。
10∶9=60∶x
10x=9×60
10x=540
x=540÷10
x=54
答:化成水后的体积是54立方分米。
【点睛】本题主要考查根据比例的基本性质列出比例,再进行解比例的能力。
24.35个
【分析】根据题意可知“前齿轮的齿数∶后齿轮的齿数=12∶7”,已知前齿轮有60个齿,如果设这辆自行车后齿轮有x个齿,则可以列出比例60∶x=12∶7。再根据比例的基本性质解比例即可。
【详解】解:设这辆自行车后齿轮有x个齿。
60∶x=12∶7
12x=60×7
x=
x=35
答:这辆自行车后齿轮有35个齿。
【点睛】此题考查了运用比例的知识解决问题。解决此题的关键是理解比例的意义、解比例的意义及掌握解比例的方法。
25.0.3米
【分析】由题意可知,设模型的高度是x米,再根据模型的高度与实际的高度比是1∶2000,列出比例解比例即可。
【详解】解:设模型的高度是x米。
x∶600=1∶2000
2000x=600×1
2000x=600
2000x÷2000=600÷2000
x=0.3
答:模型的高度是0.3米。
26.
750千米
【分析】已知一幅地图的比例尺和两个城市的图上距离,可根据图上距离∶实际距离=比例尺,列出比例方程解答即可。
【详解】解:设两个城市之间的实际距离是x厘米。
1∶30000000=2.5∶x
x=75000000
75000000厘米=750千米
答:这两个城市之间的实际距离是750千米。
【点睛】本题考查列比例方程解答问题,解答本题的关键是掌握列比例方程解答问题的方法。
27.(1)见详解
(2)见详解
(3)6;24
(4)n;n2
【分析】(1)根据长方形的特征,画出一个长为3厘米、宽为2厘米的长方形。
(2)长方形按2∶1放大,原来长方形的长和宽都乘2,即是放大后长方形的长和宽,据此画出放大后的长方形。
(3)根据长方形的面积=长×宽,分别求出原长方形和放大后的长方形的面积。
(4)长方形按2∶1放大,那么长方形的每一条边都扩大到原来的2倍;
原来长方形的周长是10厘米,放大后长方形的周长是20厘米,周长扩大到原来的2倍;
原来长方形的面积是6平方厘米,放大后长方形的面积是24平方厘米,面积扩大到原来的4倍;据此得出规律。
【详解】(1)长为3厘米、宽为2厘米的长方形如下图。
(2)放大后长方形的长是:3×2=6(厘米)
放大后长方形的宽是:2×2=4(厘米)
放大后的长方形如下图。
(3)原长方形的面积:3×2=6(平方厘米)
放大后长方形的面积:6×4=24(平方厘米)
原图的面积是6平方厘米,放大后的图形的面积是24平方厘米。
(4)观察上面的数据,可以看出把图形放大到原来的n倍,则周长扩大到原来的n倍,面积扩大到原来的n2倍。
【点睛】本题考查长方形的画法、作放大后的图形、长方形面积公式的运用以及图形放大后,图形的周长、面积的变化规律。
28.(1)反比例;(2)75块;(3)0.15平方米
【分析】(1)根据题意可知,每块地砖的面积×所需地砖的数量=总面积(一定),每块地砖的面积和所需地砖的数量的乘积一定,则它们成反比例关系;
(2)根据总面积÷每块地砖的面积=所需地砖的数量,用总面积除以0.4平方米,即可求出所需地砖的块数;
(3)根据总面积÷所需地砖的数量=每块地砖的面积,用总面积除以200块,即可求出每块地砖的面积。
【详解】(1)0.1×300=30(平方米)
0.2×150=30(平方米)
0.3×100=30(平方米)
0.5×60=30(平方米)
0.6×50=30(平方米)
每块地砖的面积和所需地砖的数量的乘积一定,则它们成反比例关系;
(2)30÷0.4=75(块)
答:如果每块地砖的面积是0.4平方米,铺这一地面需要75块地砖。
(3)300÷200=1.5(平方米)
答:铺这一地面用了200块地砖,所用的地砖每块面积是1.5平方米。
【点睛】本题考查了反比例的意义和应用,判断相关量是正比例还是反比例是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
