小升初数学仿真模拟卷二(试题)2024-2025学年数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初数学仿真模拟卷二(试题)2024-2025学年数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 15:59:07 | ||
图片预览




文档简介
/ 让教学更有效 高效备课
2024-2025学年数学六年级下册人教版
小升初数学仿真模拟卷二(试题)
一、填空题(满分20分,每小题2分)
1.(2分)某小学统计六年级学生的身高,得到的数据如下表:
身高(米) 1.40 1.43 1.46 1.48
人数 2 19 35 24
则六年级学生的平均身高为( )米(得数保留两位小数)。
2.(2分)如图是一个圆柱形饮料罐,沿着虚线把侧面商标纸剪开,展开后得到一个高为10cm,面积为188.4cm2的平行四边形,那么这个饮料罐的底面周长是( )cm,它的体积是( )cm3。
3.(2分)如图是一个轴对称图形,已知∠1∶∠2=3∶4,∠2∶∠4=2∶1,∠4的度数是( )。
4.(2分)小明时走了千米,平均每小时走了( )千米,平均每千米用( )小时。
5.(2分)0.6立方米=( )立方分米 2小时15分=( )小时
6.(2分)小北和小仑进行百米赛跑,他们同时从起点开跑(如图),当小北跑到终点时,小仑跑到了A点,小北与小仑跑步的速度比是( )∶( )。照这样的速度,假设小北退到B点开始起跑,就能和小仑同时跑到终点,则B点的位置可以表示为( )m。
7.(2分)A=2×3×n,B=3×5×n,如果A和B两数的最大公因数是27,那么n是( ),A和B的最小公倍数是( )。
8.(2分)乒乓球从高空落下,约能弹起的高度是落下高度的。如果第一次从10m的高度落下,弹起后再落下,这样,第三次它弹起高度是( )m。
9.(2分)2021年5月11日,第七次全国人口普查结果公布:全国人口共141178万人,改写成用“亿人”作单位是( )亿人,精确到个位大约是( )亿人。
10.(2分)如图每格表示100米,笑笑刚开始的位置在自己家。如果笑笑向东走100米记作“﹢100米”,则她向西走400米可记作( )米。“﹣500米”表示笑笑走到的位置是( )。
二、判断题(满分10分,每小题2分)
11.(2分)一种彩票的中奖率是1%,小明买了100张,他一定会中奖。( )
12.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
13.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
14.(2分)一个圆柱的底面半径扩大到原来的5倍,高不变,这个圆柱的体积会扩大到原来的10倍。( )
15.(2分)完成一项工程,甲队独做需要8小时,乙队独做需要6小时,则甲、乙两队工作效率之比为4∶3。( )
三、选择题(满分10分,每小题2分)
16.(2分)六(1)班共有48名学生,期末推选一名优秀毕业生,投票选举结果如下表。下方各图中,能大致表示出这个结果的是( )。
姓名 小红 小刚 小芳 小军
票数 24 12 4 8
A.B.C.D.
17.(2分)有4名同学进行200米赛跑,都要经过一个半圆形弯道,每条跑道宽1.4米,那么相邻两道的弯道相差( )米。
A.1.4 B.π C.1.4+π D.1.4π
18.(2分)下面x和y成正比例关系的是( ),成反比例关系的是( )。
①y=x+2024②x+y=2024③x=2024y④xy=2024
A.①;③ B.②;③ C.①;② D.③;④
19.(2分)水果大卖场的香蕉比桔子多4箱,比苹果少6箱。如果桔子有m箱,苹果有( )箱。
A.m+2 B.m-4 C.m+10 D.m+6
20.(2分)下面说法正确的有( )个。
①0.6米可以改写成60%米。
②我们没学圆锥表面积是因为它没有表面。
③商品打七五折销售,“七五折”表示现价是原价的75%。
④张旭家每月收入4000元,支出2500元,这是两个具有相反意义的量。
A.1 B.2 C.3 D.4
四、计算题(共22分)
21.(8分)脱式计算。(能简算的要简算)
22.(8分)求未知数x。
(1)3x+22.9=32.5 (2)
(3)(5x-5.4)÷0.5=21 (4)
23.(6分)直接写出得数。
(1)8.8+0.12= (2) (3)
(4)32÷1000= (5) (6)
五、作图题(共6分)
24.(6分)在方格纸上按要求画图。
(1)画出图形①向右平移5格后的图形。
(2)画出图形②绕点O顺时针旋转90°后的图形。
六、解答题(共32分)
25.(4分)在一幅比例尺是1∶5000000的地图上,量的A、B两地的距离是4厘米,甲乙两车分别从A、B两地同时出发相向而行,甲、乙两车的速度为每小时30千米和每小时20千米,问两车经过几小时相遇?
26.(4分)张大爷有10000元钱,现在某银行推出一年期的理财方式,年收益率为5%,每年到期后还可以连本带息继续购买下一年的这个理财产品。请问三年后,张大爷连本带息一共能得到多少元钱?
27.(4分)刘师傅去执行“抗疫物资运输”任务,第一小时行了全程的,第二小时行了全程的,还剩16千米没有行。这次“抗疫物资运输”任务全程长多少千米?
28.(5分)某游泳馆推出两种付费方式:方式一,单次卡,每次收费30元;方式二,办理会员年卡,一次缴纳240元会员费,每次游泳另外收费14元(一年内有效)。
(1)李叔叔游泳锻炼的计划是一年,每月两次。他选择哪种方式更划算?
(2)一年内游泳达到几次时,两种付费方式所用钱数相等?
29.(5分)学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
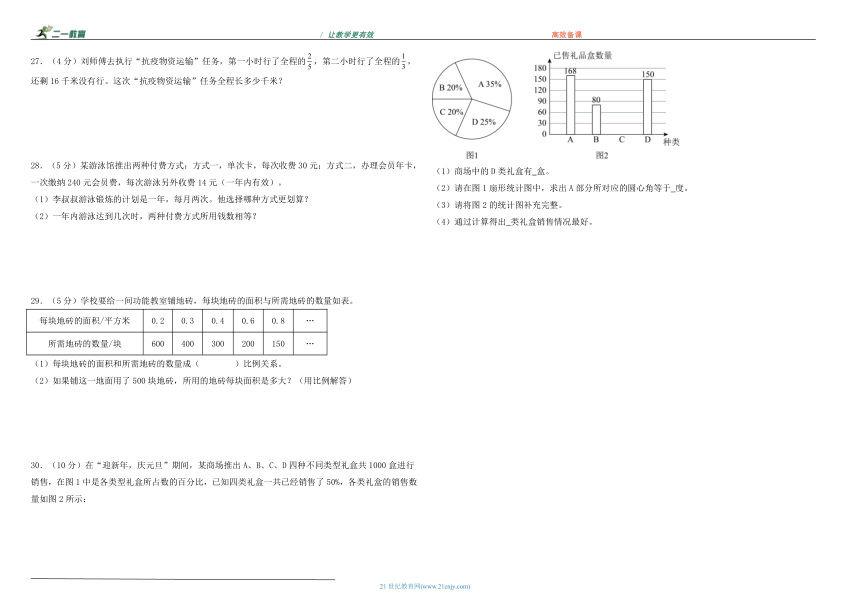
30.(10分)在“迎新年,庆元旦”期间,某商场推出A、B、C、D四种不同类型礼盒共1000盒进行销售,在图1中是各类型礼盒所占数的百分比,已知四类礼盒一共已经销售了50%,各类礼盒的销售数量如图2所示:
(1)商场中的D类礼盒有 盒。
(2)请在图1扇形统计图中,求出A部分所对应的圆心角等于 度。
(3)请将图2的统计图补充完整。
(4)通过计算得出 类礼盒销售情况最好。
参考答案
1.1.46
【分析】先把身高和对应的人数相乘,再用求出的四个数值加起来的和除以总人数,即可算出答案。
【详解】1.40×2+1.43×19+1.46×35+1.48×24
=2.80+27.17+51.1+35.52
=29.97+51.1+35.52
=80.07+35.52
=116.59(米)
总人数:2+19+35+24=80(人)
六年级学生平均身高:116.59÷80≈1.46(米)
【点睛】此题考查了学生对平均数和小数乘法的熟练掌握程度。
2.18.84 282.6
【分析】把一个圆柱形饮料罐,沿着虚线把侧面商标纸剪开,展开后得到的是平行四边形,平行四边形的底是圆柱底面周长,高是圆柱的高,圆柱的侧面积等于底面周长乘高,用侧面积除以高即可求饮料罐的底面周长,根据r=C÷π÷2求出底面半径,再根据V=πr2h求它的体积进行解答。
【详解】188.4÷10=18.84(cm)
18.84÷3.14÷2=3(cm)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(cm3)
故底面周长是18.84cm,它的体积是282.6cm3。
3.60°/60度
【分析】分析题目,根据这个四边形是轴对称图形可知:∠1=∠3,再根据求连比的方法求出∠1∶∠2∶∠4,并结合∠1=∠3写出∠1∶∠2∶∠3∶∠4,最后根据四边形的内角和是360°,用360°乘∠4占四边形内角和的几分之几即可解答。
【详解】∠2∶∠4=2∶1=(2×2)∶(1×2)=4∶2
∠1∶∠2∶∠4=3∶4∶2
因为图形是一个轴对称图形,所以∠1=∠3,所以∠1∶∠2∶∠3∶∠4=3∶4∶3∶2。
∠4=360°×=360°×=60°
如图是一个轴对称图形,已知∠1∶∠2=3∶4,∠2∶∠4=2∶1,∠4的度数是60°。
4.
【分析】求出平均每小时走的速度,根据速度=路程÷时间,用÷解答。求平均每千米用的时间,用÷解答。
【详解】÷
=×
=(千米)
÷
=×
=(小时)
小明时走了千米,平均每小时走了千米,平均每千米用小时。
5.600 2.25
【分析】根据1立方米=1000立方分米,1时=60分,单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数。
【详解】立方米化为立方分米要乘1000,
0.6立方米=600立方分米
分化为小时要除以60,
15分=0.25小时
2小时15分=2.25小时
6.5 4 ﹣25
【分析】根据题意,小北跑了100m时,小仓跑了80m,由于他们跑的时间相同,所以他们的路程比等于两人的速度比,根据比的意义得出两人的速度比,并化简比。
由上一问可知,小北与小仑跑步的速度比是5∶4,可以把小北的速度看作5份,则小仑的速度看作4份;用小仓跑的路程除以4乘5,即可算出当小仓跑到100m时,小北跑的路程;
再用小北跑的路程减去100,得出B点到起点的距离,由于B点在起点的左面,根据正负数的意义,B点的位置需用负数表示。
【详解】100∶80=(100÷20)∶(80÷20)=5∶4
小北与小仓跑步的速度比是5∶4。
当小仓跑到100m时,小北跑了:
100÷4×5
=25×5
=125(m)
B点距离起点:125-100=25(m)
B点在起点的左面,则B点的位置可以表示为﹣25m。
填空如下:
小北与小仑跑步的速度比是(5)∶(4),B点的位置可以表示为(﹣25)m。
7.9 270
【分析】根据A、B两数的分解质因数,把公有的相同质因数乘起来即是它们的最大公因数3n,已知最大公因数是27,即3n=27,据此求出n的值;
把公有的质因数与每个数独有质因数乘起来,就是它们的最小公倍数30n,据n的值代入式子中,计算出结果即可。
【详解】A=2×3×n
B=3×5×n
A和B的最大公因数是3n=27;
3n=27
n=27÷3
n=9
A和B的最小公倍数是2×3×n×5=30n;
当n=9时,30n=30×9=270
所以,n是(9),A和B的最小公倍数是(270)。
8./0.64
【分析】将第一次下落高度看作单位“1”,第一次下落高度×=第二次下落高度,再将第二次下落高度看作单位“1”,第二次下落高度×=第三次下落高度,再将第三次下落高度看作单位“1”,第三次下落高度×=第三次弹起高度。
【详解】10×××
=4××
=×
=(m)
第三次它弹起高度是m。
9.14.1178 14
【分析】改写时,如果不是整万或整亿的数,要在万位或亿位的后边,点上小数点,去掉小数点末尾的0,并加上一个“万”或“亿”字;
通过四舍五入法求小数的近似数,精确到个位要对十分位上的数进行四舍五入,若小于5则直接舍去,若大于或等于5,则向前进一位,并加上“万”或“亿”。
【详解】141178万=14.1178亿
141178万≈14亿
所以改写成用“亿人”作单位是14.1178亿人,精确到个位大约是14亿人。
10.﹣400 商场
【分析】根据负数的意义:表示具有意义相反的两种量:笑笑家为0点,向东记为正,则从笑笑家向西就记为负,直接得出结论即可。
【详解】向西走400米记作﹣400米;
500÷100=5(格)
﹣500米表示笑笑走到的位置是商场。
每格表示100米,笑笑刚开始的位置在自己家。如果笑笑向东走100米记作“﹢100米”,则她向西走400米可记作﹣400米。“﹣500米”表示笑笑走到的位置是商场。
11.×
【分析】根据概率的意义,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小的,机会大也不一定发生,概率小也可能发生,中奖率是1%,只能说明可能性的大小,并不能确定一定能中奖,据此解答。
【详解】这是一个随机事件,买彩票,中奖或不中奖都有可能,但是先无法预料,所以他可能中奖,但不是一定中奖,原题一种彩票的中奖率是1%,小明买了100张,他一定会中奖,说法错误。
故答案为:×
【点睛】本题考查可能性大小问题,解决本题的关键是知道中奖率指的是中奖的可能性,而不是说100张里一定会中一张。
12.×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【详解】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
13.√
【分析】将图形按顺时针方向旋转90°,即将图形中的每一部分都按顺时针方向旋转90°,即可得到旋转后的图形,再进行判断即可。
【详解】
根据旋转的方法可知,将按顺时针方向旋转90°,得到的图形是;原说法正确。
故答案为:√
14.×
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为V,扩大后的体积为V1,则扩大后的半径为5r,代入圆柱的体积公式,从而可以求出它的体积扩大到原来的几倍。
【详解】设圆柱底面半径为r,高为h
原来的体积:V=πr2h
扩大后的体积:
V1=π(5r)2h
=π×5r×5r×h
=25πr2h
25πr2h÷πr2h=25
一个圆柱的底面半径扩大到原来的5倍,高不变,这个圆柱的体积会扩大到原来的25倍。原题干说法错误。
故答案为:×
15.×
【分析】根据工作量÷工作时间=工作效率分别求出甲乙两队的工作效率比,再化成最简整数比。
【详解】1÷8=
1÷6=
∶
=(×24)∶(×24)
=3∶4
甲、乙两队工作效率之比为3∶4,所以原题说法错误。
故答案为:×
16.A
【分析】先分别计算四位学生所得票数占48的百分之几,再观察四个选项中的扇形统计图,找出能大致表示出这个结果的扇形统计图。
【详解】小红:24÷48=50%
小刚:12÷48=25%
小芳:4÷48≈8.3%
小军:8÷48≈16.7%
50%是整个圆的一半;25%是整个圆的;16.7%和8.3%一共占整个圆的,且8票是4票的2倍。
A.如左图,A选项正确。
B.中没有扇形占整个圆的50%,B选项错误。
C.中没有扇形占整个圆的25%,C选项错误。
D.中16.7%和8.3%一共占整个圆的,但没有体现8票是4票的2倍,D选项错误。
故答案为:A
17.D
【分析】根据题意可知,进行200米赛跑,要经过一个弯道,相邻两道的弯道差也就是外圆与内圆周长一半的差,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】设弯道内圆的半径为r米,则外圆的半径是(r+1.4)米。
π(r+1.4)-πr
=πr+1.4π-πr
=1.4π(米)
相邻两道的弯道相差1.4π米。
故答案为:D
18.D
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是比值或乘积一定,就不成比例。
【详解】①y=x+2024,则y-x=2024,x和y不成比例;
②x+y=2024,x和y不成比例;
③x=2024y,x∶y=2024,比值一定,所以y和x成正比例;
④xy=2024,乘积一定,所以x和y成反比例。
所以x和y成正比例关系的是③,成反比例关系的是④。
故答案为:D
19.C
【分析】分析题目,先用桔子的箱数加上4求出香蕉的箱数,再用香蕉的箱数加上6即可得到苹果的箱数。
【详解】m+4+6=(m+10)箱
水果大卖场的香蕉比桔子多4箱,比苹果少6箱。如果桔子有m箱,苹果有(m+10)箱。
故答案为:C
20.B
【分析】①百分数(又叫作百分率或百分比)与分数的意义截然不同。百分数表示一个数是另一个数的百分之几,它只能表示两数之间的倍比关系,不能表示具体的量,因此,百分数后面不能带单位名称,分数后面可以带单位名称;
②立体图形的所有面的面积之和叫作表面积;
③商店有时降价出售商品,叫作打折扣销售,俗称“打折”,几折就表示十分之几,也就是百分之几十,如:打九折出售,就是按原价的90%出售,八五折就是原价的85%;
④正负数主要用来表示具有相反意义的两种量,如果规定其中一个为正,那么相反的量就用负表示,收入可以表示为“﹢”,那么支出可以表示为“﹣”,据此解答。
【详解】①分析可知,0.6米不能改写成60%米,所以题目说法错误;
②圆锥属于立体图形,那么圆锥有表面积,所以题目说法错误;
③分析可知,商品打七五折销售,“七五折”表示现价是原价的75%,所以题目说法正确;
④收入可以用“﹢”表示,支出可以用“﹣”表示,收入4000元(﹢4000)和支出2500元(﹣2500)是两个具有相反意义的量,所以题目说法正确。
综上所述,说法正确的有③④,一共2个。
故答案为:B
21.24990;11;
38;
【分析】(1)先把拆成,然后根据乘法分配律(a+b)×c=a×c+b×c把变成,再按顺序计算;
(2)先交换“”和“”的位置,然后根据减法的性质a-b-c=a-(b+c)把变成,再按顺序计算;
(3)根据乘法分配律(a+b)×c=a×c+b×c把变成,再按顺序计算;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
(4)
22.(1)x=3.2;(2)x=;
(3)x=3.18;(4)x=0.6
【分析】(1)根据等式的性质,方程的两边同时减去22.9,然后方程的两边同时除以3求解;
(2)根据比例的基本性质,把原式化为x=×,然后根据等式的性质,方程的两边同时除以求解;
(3)根据等式的性质,方程的两边同时乘0.5,方程的两边同时加上5.4,然后方程的两边同时除以5求解;
(4)根据比例的基本性质,把原式化为5x×4=2.4×5,再把方程化为20x=12,最后根据等式的性质,方程的两边同时除以20求解。
【详解】(1)3x+22.9=32.5
解:3x+22.9-22.9=32.5-22.9
3x=9.6
3x÷3=9.6÷3
x=3.2
(2)
解:x=×
x=
x÷=÷
x=×12
x=
(3)(5x-5.4)÷0.5=21
解:(5x-5.4)÷0.5×0.5=21×0.5
5x-5.4=10.5
5x-5.4+5.4=10.5+5.4
5x=15.9
5x÷5=15.9÷5
x=3.18
(4)
解:5x×4=2.4×5
20x=12
20x÷20=12÷20
x=0.6
23.(1)8.92;(2);(3);
(4)0.032;(5);(6)
24.见详解
【分析】(1)根据平移的特征,将图形①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图形②绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】如图:
25.4小时
【分析】已知图上距离÷比例尺=实际距离,求出实际距离,再根据“路程和÷速度和=相遇时间”,代入数据即可求出乙车的速度。
【详解】4÷
=4×5000000
=20000000(厘米)
20000000厘米=200千米
200÷(30+20)
=200÷50
=4(小时)
答:两车经过4小时相遇。
26.11576.25元
【分析】根据题意,我们知道张大爷的本金是10000元,年收益率是5%,所以我们可以根据本息和=本金×存期×(1+利率),先计算出第一年的本息和,然后再用这个结果去计算第二年的本息和,最后再用第二年的结果去计算第三年的本息和,据此解答即可。
【详解】10000×(1+5%)×(1+5%)×(1+5%)
=10000×1.05×1.05×1.05
=10500××1.05×1.05
=11025×1.05
=11576.25(元)
答:三年后,张大爷连本带息一共能得到11576.25元钱。
27.60千米
【分析】把全程看作单位“1”,用1减去前面两个小时所行驶路程对应的分率,得出剩下未行驶路程对应的分率,再根据已知一个数的几分之几是多少,求这个数,用除法求解即可。
【详解】
=
=
=60(千米)
答:这次“抗疫物资运输”任务全程长60千米。
【点睛】本题主要考查的是分数除法的应用,求出剩余路程对应的分率是解题的关键。
28.(1)方式二
(2)15次
【分析】(1)分别计算出两种方式的实际钱数,比较即可。一年有12个月,方式一:单价×数量=总价,每月次数×月数=总次数,单价×总次数=实际钱数;方式二:每次另外收费钱数×总次数,然后再加上240元的会员费是实际钱数。
(2)两种方式,游泳次数相同,每次相差16元,240元里面有几个16元,就有几次。
【详解】(1)方式一:30×(12×2)
=30×24
=720(元)
方式二:240+14×(12×2)
=240+14×24
=240+336
=576(元)
720>576
答:他选择方式二更划算。
(2)240÷(30-14)
=240÷16
=15(次)
答:一年内游泳达到15次时,两种付费方式所用钱数相等。
29.(1)反
(2)0.24平方米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
(2)因为功能教室地面的总面积是一定的,所以每块地砖的面积和所需地砖的数量成反比例关系,我们可以据此列比例式来求解;设所用的地砖每块面积是x平方米。因为地面总面积一定,每块地砖面积和所需地砖数量成反比例,所以可列方程500x= 0.2×600。
【详解】(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=…=120(一定),乘积一定,所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)如果铺这一地面用了500块地砖,设所用的地砖每块面积是x平方米。
500x=0.2×600
500x=120
x=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
30.(1)250
(2)126
(3)见详解
(4)A
【分析】(1)已知四种不同类型礼盒共1000盒,从图1可知D类礼盒所占百分比为25%。
根据“部分数量=整体数量×部分所占百分比”,可得D类礼盒数量;
(2)在扇形统计图中,圆心角的度数=该部分所占百分比×360°。从图1可知A类礼盒所占百分比为35%,据此代入数据解答;
(3)已知四类礼盒一共已经销售了50%,则已销售礼盒总数为1000×50%=500盒。从图2可知A类已售168盒,B类已售80盒,D类已售150盒。那么C类已售数量为已销售礼盒总数减去A、B、D类已售数量,即500-168-80-150=332-80-150=252-150=102盒。据此可在图2中补充C类礼盒已售数量的条形图。
(4)从图2可知,A类礼盒已售168盒,B类礼盒已售80盒,C类礼盒已售102盒,D类礼盒已售150盒,用各类礼盒的销量除以总量,求出它们各自销售的百分比,再进行比较即可。
【详解】(1)1000×25%=250(盒)
所以商场中的D类礼盒有250盒。
(2)360×35%=126(度)
所以A部分所对应的圆心角等于126度。
(3)500-168-80-150
=332-80-150
=252-150
=102(盒)
(4)从图2可知,A类礼盒已售168盒,B类礼盒已售80盒,C类礼盒已售102盒,D类礼盒已售150盒。
168÷500×100%=0.336×100%=33.6%
80÷500×100%=0.16×100%=16%
102÷500×100%=0.204×100%=20.4%
150÷500×100%=0.3×100%=30%
因为33.6%>30%>20.4%>16%,所以A类礼盒销售情况最好。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年数学六年级下册人教版
小升初数学仿真模拟卷二(试题)
一、填空题(满分20分,每小题2分)
1.(2分)某小学统计六年级学生的身高,得到的数据如下表:
身高(米) 1.40 1.43 1.46 1.48
人数 2 19 35 24
则六年级学生的平均身高为( )米(得数保留两位小数)。
2.(2分)如图是一个圆柱形饮料罐,沿着虚线把侧面商标纸剪开,展开后得到一个高为10cm,面积为188.4cm2的平行四边形,那么这个饮料罐的底面周长是( )cm,它的体积是( )cm3。
3.(2分)如图是一个轴对称图形,已知∠1∶∠2=3∶4,∠2∶∠4=2∶1,∠4的度数是( )。
4.(2分)小明时走了千米,平均每小时走了( )千米,平均每千米用( )小时。
5.(2分)0.6立方米=( )立方分米 2小时15分=( )小时
6.(2分)小北和小仑进行百米赛跑,他们同时从起点开跑(如图),当小北跑到终点时,小仑跑到了A点,小北与小仑跑步的速度比是( )∶( )。照这样的速度,假设小北退到B点开始起跑,就能和小仑同时跑到终点,则B点的位置可以表示为( )m。
7.(2分)A=2×3×n,B=3×5×n,如果A和B两数的最大公因数是27,那么n是( ),A和B的最小公倍数是( )。
8.(2分)乒乓球从高空落下,约能弹起的高度是落下高度的。如果第一次从10m的高度落下,弹起后再落下,这样,第三次它弹起高度是( )m。
9.(2分)2021年5月11日,第七次全国人口普查结果公布:全国人口共141178万人,改写成用“亿人”作单位是( )亿人,精确到个位大约是( )亿人。
10.(2分)如图每格表示100米,笑笑刚开始的位置在自己家。如果笑笑向东走100米记作“﹢100米”,则她向西走400米可记作( )米。“﹣500米”表示笑笑走到的位置是( )。
二、判断题(满分10分,每小题2分)
11.(2分)一种彩票的中奖率是1%,小明买了100张,他一定会中奖。( )
12.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
13.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
14.(2分)一个圆柱的底面半径扩大到原来的5倍,高不变,这个圆柱的体积会扩大到原来的10倍。( )
15.(2分)完成一项工程,甲队独做需要8小时,乙队独做需要6小时,则甲、乙两队工作效率之比为4∶3。( )
三、选择题(满分10分,每小题2分)
16.(2分)六(1)班共有48名学生,期末推选一名优秀毕业生,投票选举结果如下表。下方各图中,能大致表示出这个结果的是( )。
姓名 小红 小刚 小芳 小军
票数 24 12 4 8
A.B.C.D.
17.(2分)有4名同学进行200米赛跑,都要经过一个半圆形弯道,每条跑道宽1.4米,那么相邻两道的弯道相差( )米。
A.1.4 B.π C.1.4+π D.1.4π
18.(2分)下面x和y成正比例关系的是( ),成反比例关系的是( )。
①y=x+2024②x+y=2024③x=2024y④xy=2024
A.①;③ B.②;③ C.①;② D.③;④
19.(2分)水果大卖场的香蕉比桔子多4箱,比苹果少6箱。如果桔子有m箱,苹果有( )箱。
A.m+2 B.m-4 C.m+10 D.m+6
20.(2分)下面说法正确的有( )个。
①0.6米可以改写成60%米。
②我们没学圆锥表面积是因为它没有表面。
③商品打七五折销售,“七五折”表示现价是原价的75%。
④张旭家每月收入4000元,支出2500元,这是两个具有相反意义的量。
A.1 B.2 C.3 D.4
四、计算题(共22分)
21.(8分)脱式计算。(能简算的要简算)
22.(8分)求未知数x。
(1)3x+22.9=32.5 (2)
(3)(5x-5.4)÷0.5=21 (4)
23.(6分)直接写出得数。
(1)8.8+0.12= (2) (3)
(4)32÷1000= (5) (6)
五、作图题(共6分)
24.(6分)在方格纸上按要求画图。
(1)画出图形①向右平移5格后的图形。
(2)画出图形②绕点O顺时针旋转90°后的图形。
六、解答题(共32分)
25.(4分)在一幅比例尺是1∶5000000的地图上,量的A、B两地的距离是4厘米,甲乙两车分别从A、B两地同时出发相向而行,甲、乙两车的速度为每小时30千米和每小时20千米,问两车经过几小时相遇?
26.(4分)张大爷有10000元钱,现在某银行推出一年期的理财方式,年收益率为5%,每年到期后还可以连本带息继续购买下一年的这个理财产品。请问三年后,张大爷连本带息一共能得到多少元钱?
27.(4分)刘师傅去执行“抗疫物资运输”任务,第一小时行了全程的,第二小时行了全程的,还剩16千米没有行。这次“抗疫物资运输”任务全程长多少千米?
28.(5分)某游泳馆推出两种付费方式:方式一,单次卡,每次收费30元;方式二,办理会员年卡,一次缴纳240元会员费,每次游泳另外收费14元(一年内有效)。
(1)李叔叔游泳锻炼的计划是一年,每月两次。他选择哪种方式更划算?
(2)一年内游泳达到几次时,两种付费方式所用钱数相等?
29.(5分)学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
30.(10分)在“迎新年,庆元旦”期间,某商场推出A、B、C、D四种不同类型礼盒共1000盒进行销售,在图1中是各类型礼盒所占数的百分比,已知四类礼盒一共已经销售了50%,各类礼盒的销售数量如图2所示:
(1)商场中的D类礼盒有 盒。
(2)请在图1扇形统计图中,求出A部分所对应的圆心角等于 度。
(3)请将图2的统计图补充完整。
(4)通过计算得出 类礼盒销售情况最好。
参考答案
1.1.46
【分析】先把身高和对应的人数相乘,再用求出的四个数值加起来的和除以总人数,即可算出答案。
【详解】1.40×2+1.43×19+1.46×35+1.48×24
=2.80+27.17+51.1+35.52
=29.97+51.1+35.52
=80.07+35.52
=116.59(米)
总人数:2+19+35+24=80(人)
六年级学生平均身高:116.59÷80≈1.46(米)
【点睛】此题考查了学生对平均数和小数乘法的熟练掌握程度。
2.18.84 282.6
【分析】把一个圆柱形饮料罐,沿着虚线把侧面商标纸剪开,展开后得到的是平行四边形,平行四边形的底是圆柱底面周长,高是圆柱的高,圆柱的侧面积等于底面周长乘高,用侧面积除以高即可求饮料罐的底面周长,根据r=C÷π÷2求出底面半径,再根据V=πr2h求它的体积进行解答。
【详解】188.4÷10=18.84(cm)
18.84÷3.14÷2=3(cm)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(cm3)
故底面周长是18.84cm,它的体积是282.6cm3。
3.60°/60度
【分析】分析题目,根据这个四边形是轴对称图形可知:∠1=∠3,再根据求连比的方法求出∠1∶∠2∶∠4,并结合∠1=∠3写出∠1∶∠2∶∠3∶∠4,最后根据四边形的内角和是360°,用360°乘∠4占四边形内角和的几分之几即可解答。
【详解】∠2∶∠4=2∶1=(2×2)∶(1×2)=4∶2
∠1∶∠2∶∠4=3∶4∶2
因为图形是一个轴对称图形,所以∠1=∠3,所以∠1∶∠2∶∠3∶∠4=3∶4∶3∶2。
∠4=360°×=360°×=60°
如图是一个轴对称图形,已知∠1∶∠2=3∶4,∠2∶∠4=2∶1,∠4的度数是60°。
4.
【分析】求出平均每小时走的速度,根据速度=路程÷时间,用÷解答。求平均每千米用的时间,用÷解答。
【详解】÷
=×
=(千米)
÷
=×
=(小时)
小明时走了千米,平均每小时走了千米,平均每千米用小时。
5.600 2.25
【分析】根据1立方米=1000立方分米,1时=60分,单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数。
【详解】立方米化为立方分米要乘1000,
0.6立方米=600立方分米
分化为小时要除以60,
15分=0.25小时
2小时15分=2.25小时
6.5 4 ﹣25
【分析】根据题意,小北跑了100m时,小仓跑了80m,由于他们跑的时间相同,所以他们的路程比等于两人的速度比,根据比的意义得出两人的速度比,并化简比。
由上一问可知,小北与小仑跑步的速度比是5∶4,可以把小北的速度看作5份,则小仑的速度看作4份;用小仓跑的路程除以4乘5,即可算出当小仓跑到100m时,小北跑的路程;
再用小北跑的路程减去100,得出B点到起点的距离,由于B点在起点的左面,根据正负数的意义,B点的位置需用负数表示。
【详解】100∶80=(100÷20)∶(80÷20)=5∶4
小北与小仓跑步的速度比是5∶4。
当小仓跑到100m时,小北跑了:
100÷4×5
=25×5
=125(m)
B点距离起点:125-100=25(m)
B点在起点的左面,则B点的位置可以表示为﹣25m。
填空如下:
小北与小仑跑步的速度比是(5)∶(4),B点的位置可以表示为(﹣25)m。
7.9 270
【分析】根据A、B两数的分解质因数,把公有的相同质因数乘起来即是它们的最大公因数3n,已知最大公因数是27,即3n=27,据此求出n的值;
把公有的质因数与每个数独有质因数乘起来,就是它们的最小公倍数30n,据n的值代入式子中,计算出结果即可。
【详解】A=2×3×n
B=3×5×n
A和B的最大公因数是3n=27;
3n=27
n=27÷3
n=9
A和B的最小公倍数是2×3×n×5=30n;
当n=9时,30n=30×9=270
所以,n是(9),A和B的最小公倍数是(270)。
8./0.64
【分析】将第一次下落高度看作单位“1”,第一次下落高度×=第二次下落高度,再将第二次下落高度看作单位“1”,第二次下落高度×=第三次下落高度,再将第三次下落高度看作单位“1”,第三次下落高度×=第三次弹起高度。
【详解】10×××
=4××
=×
=(m)
第三次它弹起高度是m。
9.14.1178 14
【分析】改写时,如果不是整万或整亿的数,要在万位或亿位的后边,点上小数点,去掉小数点末尾的0,并加上一个“万”或“亿”字;
通过四舍五入法求小数的近似数,精确到个位要对十分位上的数进行四舍五入,若小于5则直接舍去,若大于或等于5,则向前进一位,并加上“万”或“亿”。
【详解】141178万=14.1178亿
141178万≈14亿
所以改写成用“亿人”作单位是14.1178亿人,精确到个位大约是14亿人。
10.﹣400 商场
【分析】根据负数的意义:表示具有意义相反的两种量:笑笑家为0点,向东记为正,则从笑笑家向西就记为负,直接得出结论即可。
【详解】向西走400米记作﹣400米;
500÷100=5(格)
﹣500米表示笑笑走到的位置是商场。
每格表示100米,笑笑刚开始的位置在自己家。如果笑笑向东走100米记作“﹢100米”,则她向西走400米可记作﹣400米。“﹣500米”表示笑笑走到的位置是商场。
11.×
【分析】根据概率的意义,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小的,机会大也不一定发生,概率小也可能发生,中奖率是1%,只能说明可能性的大小,并不能确定一定能中奖,据此解答。
【详解】这是一个随机事件,买彩票,中奖或不中奖都有可能,但是先无法预料,所以他可能中奖,但不是一定中奖,原题一种彩票的中奖率是1%,小明买了100张,他一定会中奖,说法错误。
故答案为:×
【点睛】本题考查可能性大小问题,解决本题的关键是知道中奖率指的是中奖的可能性,而不是说100张里一定会中一张。
12.×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【详解】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
13.√
【分析】将图形按顺时针方向旋转90°,即将图形中的每一部分都按顺时针方向旋转90°,即可得到旋转后的图形,再进行判断即可。
【详解】
根据旋转的方法可知,将按顺时针方向旋转90°,得到的图形是;原说法正确。
故答案为:√
14.×
【分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为V,扩大后的体积为V1,则扩大后的半径为5r,代入圆柱的体积公式,从而可以求出它的体积扩大到原来的几倍。
【详解】设圆柱底面半径为r,高为h
原来的体积:V=πr2h
扩大后的体积:
V1=π(5r)2h
=π×5r×5r×h
=25πr2h
25πr2h÷πr2h=25
一个圆柱的底面半径扩大到原来的5倍,高不变,这个圆柱的体积会扩大到原来的25倍。原题干说法错误。
故答案为:×
15.×
【分析】根据工作量÷工作时间=工作效率分别求出甲乙两队的工作效率比,再化成最简整数比。
【详解】1÷8=
1÷6=
∶
=(×24)∶(×24)
=3∶4
甲、乙两队工作效率之比为3∶4,所以原题说法错误。
故答案为:×
16.A
【分析】先分别计算四位学生所得票数占48的百分之几,再观察四个选项中的扇形统计图,找出能大致表示出这个结果的扇形统计图。
【详解】小红:24÷48=50%
小刚:12÷48=25%
小芳:4÷48≈8.3%
小军:8÷48≈16.7%
50%是整个圆的一半;25%是整个圆的;16.7%和8.3%一共占整个圆的,且8票是4票的2倍。
A.如左图,A选项正确。
B.中没有扇形占整个圆的50%,B选项错误。
C.中没有扇形占整个圆的25%,C选项错误。
D.中16.7%和8.3%一共占整个圆的,但没有体现8票是4票的2倍,D选项错误。
故答案为:A
17.D
【分析】根据题意可知,进行200米赛跑,要经过一个弯道,相邻两道的弯道差也就是外圆与内圆周长一半的差,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】设弯道内圆的半径为r米,则外圆的半径是(r+1.4)米。
π(r+1.4)-πr
=πr+1.4π-πr
=1.4π(米)
相邻两道的弯道相差1.4π米。
故答案为:D
18.D
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是比值或乘积一定,就不成比例。
【详解】①y=x+2024,则y-x=2024,x和y不成比例;
②x+y=2024,x和y不成比例;
③x=2024y,x∶y=2024,比值一定,所以y和x成正比例;
④xy=2024,乘积一定,所以x和y成反比例。
所以x和y成正比例关系的是③,成反比例关系的是④。
故答案为:D
19.C
【分析】分析题目,先用桔子的箱数加上4求出香蕉的箱数,再用香蕉的箱数加上6即可得到苹果的箱数。
【详解】m+4+6=(m+10)箱
水果大卖场的香蕉比桔子多4箱,比苹果少6箱。如果桔子有m箱,苹果有(m+10)箱。
故答案为:C
20.B
【分析】①百分数(又叫作百分率或百分比)与分数的意义截然不同。百分数表示一个数是另一个数的百分之几,它只能表示两数之间的倍比关系,不能表示具体的量,因此,百分数后面不能带单位名称,分数后面可以带单位名称;
②立体图形的所有面的面积之和叫作表面积;
③商店有时降价出售商品,叫作打折扣销售,俗称“打折”,几折就表示十分之几,也就是百分之几十,如:打九折出售,就是按原价的90%出售,八五折就是原价的85%;
④正负数主要用来表示具有相反意义的两种量,如果规定其中一个为正,那么相反的量就用负表示,收入可以表示为“﹢”,那么支出可以表示为“﹣”,据此解答。
【详解】①分析可知,0.6米不能改写成60%米,所以题目说法错误;
②圆锥属于立体图形,那么圆锥有表面积,所以题目说法错误;
③分析可知,商品打七五折销售,“七五折”表示现价是原价的75%,所以题目说法正确;
④收入可以用“﹢”表示,支出可以用“﹣”表示,收入4000元(﹢4000)和支出2500元(﹣2500)是两个具有相反意义的量,所以题目说法正确。
综上所述,说法正确的有③④,一共2个。
故答案为:B
21.24990;11;
38;
【分析】(1)先把拆成,然后根据乘法分配律(a+b)×c=a×c+b×c把变成,再按顺序计算;
(2)先交换“”和“”的位置,然后根据减法的性质a-b-c=a-(b+c)把变成,再按顺序计算;
(3)根据乘法分配律(a+b)×c=a×c+b×c把变成,再按顺序计算;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
(4)
22.(1)x=3.2;(2)x=;
(3)x=3.18;(4)x=0.6
【分析】(1)根据等式的性质,方程的两边同时减去22.9,然后方程的两边同时除以3求解;
(2)根据比例的基本性质,把原式化为x=×,然后根据等式的性质,方程的两边同时除以求解;
(3)根据等式的性质,方程的两边同时乘0.5,方程的两边同时加上5.4,然后方程的两边同时除以5求解;
(4)根据比例的基本性质,把原式化为5x×4=2.4×5,再把方程化为20x=12,最后根据等式的性质,方程的两边同时除以20求解。
【详解】(1)3x+22.9=32.5
解:3x+22.9-22.9=32.5-22.9
3x=9.6
3x÷3=9.6÷3
x=3.2
(2)
解:x=×
x=
x÷=÷
x=×12
x=
(3)(5x-5.4)÷0.5=21
解:(5x-5.4)÷0.5×0.5=21×0.5
5x-5.4=10.5
5x-5.4+5.4=10.5+5.4
5x=15.9
5x÷5=15.9÷5
x=3.18
(4)
解:5x×4=2.4×5
20x=12
20x÷20=12÷20
x=0.6
23.(1)8.92;(2);(3);
(4)0.032;(5);(6)
24.见详解
【分析】(1)根据平移的特征,将图形①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图形②绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】如图:
25.4小时
【分析】已知图上距离÷比例尺=实际距离,求出实际距离,再根据“路程和÷速度和=相遇时间”,代入数据即可求出乙车的速度。
【详解】4÷
=4×5000000
=20000000(厘米)
20000000厘米=200千米
200÷(30+20)
=200÷50
=4(小时)
答:两车经过4小时相遇。
26.11576.25元
【分析】根据题意,我们知道张大爷的本金是10000元,年收益率是5%,所以我们可以根据本息和=本金×存期×(1+利率),先计算出第一年的本息和,然后再用这个结果去计算第二年的本息和,最后再用第二年的结果去计算第三年的本息和,据此解答即可。
【详解】10000×(1+5%)×(1+5%)×(1+5%)
=10000×1.05×1.05×1.05
=10500××1.05×1.05
=11025×1.05
=11576.25(元)
答:三年后,张大爷连本带息一共能得到11576.25元钱。
27.60千米
【分析】把全程看作单位“1”,用1减去前面两个小时所行驶路程对应的分率,得出剩下未行驶路程对应的分率,再根据已知一个数的几分之几是多少,求这个数,用除法求解即可。
【详解】
=
=
=60(千米)
答:这次“抗疫物资运输”任务全程长60千米。
【点睛】本题主要考查的是分数除法的应用,求出剩余路程对应的分率是解题的关键。
28.(1)方式二
(2)15次
【分析】(1)分别计算出两种方式的实际钱数,比较即可。一年有12个月,方式一:单价×数量=总价,每月次数×月数=总次数,单价×总次数=实际钱数;方式二:每次另外收费钱数×总次数,然后再加上240元的会员费是实际钱数。
(2)两种方式,游泳次数相同,每次相差16元,240元里面有几个16元,就有几次。
【详解】(1)方式一:30×(12×2)
=30×24
=720(元)
方式二:240+14×(12×2)
=240+14×24
=240+336
=576(元)
720>576
答:他选择方式二更划算。
(2)240÷(30-14)
=240÷16
=15(次)
答:一年内游泳达到15次时,两种付费方式所用钱数相等。
29.(1)反
(2)0.24平方米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
(2)因为功能教室地面的总面积是一定的,所以每块地砖的面积和所需地砖的数量成反比例关系,我们可以据此列比例式来求解;设所用的地砖每块面积是x平方米。因为地面总面积一定,每块地砖面积和所需地砖数量成反比例,所以可列方程500x= 0.2×600。
【详解】(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=…=120(一定),乘积一定,所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)如果铺这一地面用了500块地砖,设所用的地砖每块面积是x平方米。
500x=0.2×600
500x=120
x=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
30.(1)250
(2)126
(3)见详解
(4)A
【分析】(1)已知四种不同类型礼盒共1000盒,从图1可知D类礼盒所占百分比为25%。
根据“部分数量=整体数量×部分所占百分比”,可得D类礼盒数量;
(2)在扇形统计图中,圆心角的度数=该部分所占百分比×360°。从图1可知A类礼盒所占百分比为35%,据此代入数据解答;
(3)已知四类礼盒一共已经销售了50%,则已销售礼盒总数为1000×50%=500盒。从图2可知A类已售168盒,B类已售80盒,D类已售150盒。那么C类已售数量为已销售礼盒总数减去A、B、D类已售数量,即500-168-80-150=332-80-150=252-150=102盒。据此可在图2中补充C类礼盒已售数量的条形图。
(4)从图2可知,A类礼盒已售168盒,B类礼盒已售80盒,C类礼盒已售102盒,D类礼盒已售150盒,用各类礼盒的销量除以总量,求出它们各自销售的百分比,再进行比较即可。
【详解】(1)1000×25%=250(盒)
所以商场中的D类礼盒有250盒。
(2)360×35%=126(度)
所以A部分所对应的圆心角等于126度。
(3)500-168-80-150
=332-80-150
=252-150
=102(盒)
(4)从图2可知,A类礼盒已售168盒,B类礼盒已售80盒,C类礼盒已售102盒,D类礼盒已售150盒。
168÷500×100%=0.336×100%=33.6%
80÷500×100%=0.16×100%=16%
102÷500×100%=0.204×100%=20.4%
150÷500×100%=0.3×100%=30%
因为33.6%>30%>20.4%>16%,所以A类礼盒销售情况最好。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
