沪科版七下(2024版)9.2.2 分式的加减(1) 课件
文档属性
| 名称 | 沪科版七下(2024版)9.2.2 分式的加减(1) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 16:37:19 | ||
图片预览








文档简介
(共24张PPT)
第9章 分式
9.2.2 分式的加减(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能准确描述最简公分母的定义,熟练运用因式分解确定最简公分母,并完成分式通分。
01
通过类比分数通分、自主推导最简公分母的确定方法,培养逻辑推理与运算能力。
02
在规范运算中体会数学的严谨性,通过解决实际问题感受数学的应用价值。
03
02
新知导入
乘法法则:两个分式相乘,用分子的积作积的分子,用分母的积作积的分母.
除法法则:两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示= , =
分式乘方的法则:分式乘方等于把分子、分母分别乘方.
02
新知导入
分数的加减:
相同分母:如果分母相同,只需将分子相加或相减,分母保持不变。
不同分母:如果分母不同,首先需要通分,将分数转换为相同的分母,然后再进行加减运算。
通分:找到两个分母的最小公倍数,转换成同分母的加减法。
注意:确保结果是最简分数形式,即分子和分母没有公因数,无法再约分。
03
新知探究
1.下面再来复习分数的加减运算:
(1)+=_______; (2)=_______;
(3)()+()=_______; (4)()()=_______.
2.类比分数的加减运算,下面分式的加减运算如何进行?
(1);(2);(3)(4)
2
1
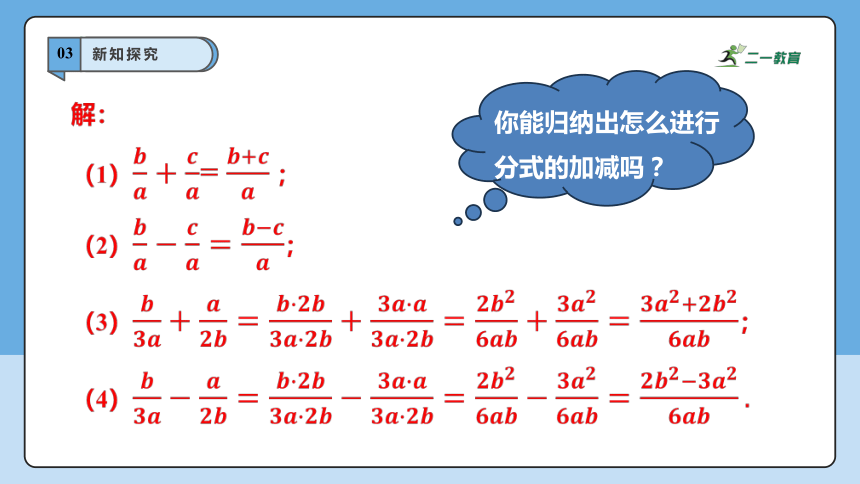
解:
(1)= ;
(2);
(3);
(4)
03
新知探究
你能归纳出怎么进行分式的加减吗?
归纳
同分母分式相加减:同分母分式相加减,分母不变,把分子相加减,即= .
异分母分式相加减:异分母分式相加减,先通分,变为同分母分式,再加减,即.
03
新知探究
通分的概念 :
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减。化异分母的分式为同分母的分式的过程,叫作分式的通分。
03
新知探究
最简公分母的概念 :
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
03
新知探究
例3
通分:(1),,;
解: (1) 3,4,12ab中系数的最小公倍数为12,字母a的最高次幂为,字母b的最高次幂为,故公分母为12,
通分后分别为:=, =,.
如果各分母的系数都是整数时,通常取它们系数的最小公倍数作为最简公分母的系数。
03
新知探究
例3
通分:(2),,.
解: (2) x2y2=(xy)(x+y),x2+2xy+y2=(x+y) 2,x2+xy=x(x+y),
故公分母为x(x+y)2(xy).
通分后分别为:===.
当分母是多项式时,一般应先分解因式.
04
课堂练习
【知识技能类作业】必做题:
1.把分式通分时,这三个分式的分子分母依次乘 、
、 .
2.分式、的最简公分母是 ,通分为 .
04
课堂练习
【知识技能类作业】必做题:
3.填空:① ,②,括号内依次填入 , .
04
课堂练习
【知识技能类作业】选做题:
4.分式的分母经过通分后变成,那么分子应变为 .
5.当时, .
6.分式与通分后的结果是 .
,
04
课堂练习
【综合拓展类作业】
7.求出下列各组分式的最简公分母.
(1); (2);
(3); (4).
(1)解:和的最简公分母是;
(2)解:的最简公分母是;
04
课堂练习
【综合拓展类作业】
(3); (4).
(3)解:的最简公分母是;
(4)解:的最简公分母是.
05
课堂小结
如何确定分式的最简公分母:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
06
作业布置
【知识技能类作业】
1.在计算通分时,分母确定为( )
A. B. C. D.
2.只把分式中的m,n同时扩大为原来的3倍后,分式的值也不会变,则此时a的值可以是下列中的( )
A.2 B.mn C.m D.m2
B
C
06
作业布置
【知识技能类作业】
3.把分式,,通分,下列结论错误的是( )
A.最简公分母是(x-2)(x+1)2
B. =
C. =
D. =
D
06
作业布置
【综合拓展类作业】
4.甲完成一项工作需要天,乙完成这项工作要比甲多8天,设工作总量为1,写出表示甲、乙两人工作效率的式子,若两式的分母不同,则将两个式子进行通分.
解:甲的工作效率为,乙的工作效率为.
,
.
07
板书设计
同分母:
异分母:
通分:
最简公分母:
9.2.2 分式的加减(1)
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第9章 分式
9.2.2 分式的加减(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能准确描述最简公分母的定义,熟练运用因式分解确定最简公分母,并完成分式通分。
01
通过类比分数通分、自主推导最简公分母的确定方法,培养逻辑推理与运算能力。
02
在规范运算中体会数学的严谨性,通过解决实际问题感受数学的应用价值。
03
02
新知导入
乘法法则:两个分式相乘,用分子的积作积的分子,用分母的积作积的分母.
除法法则:两个分式相除,将除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示= , =
分式乘方的法则:分式乘方等于把分子、分母分别乘方.
02
新知导入
分数的加减:
相同分母:如果分母相同,只需将分子相加或相减,分母保持不变。
不同分母:如果分母不同,首先需要通分,将分数转换为相同的分母,然后再进行加减运算。
通分:找到两个分母的最小公倍数,转换成同分母的加减法。
注意:确保结果是最简分数形式,即分子和分母没有公因数,无法再约分。
03
新知探究
1.下面再来复习分数的加减运算:
(1)+=_______; (2)=_______;
(3)()+()=_______; (4)()()=_______.
2.类比分数的加减运算,下面分式的加减运算如何进行?
(1);(2);(3)(4)
2
1
解:
(1)= ;
(2);
(3);
(4)
03
新知探究
你能归纳出怎么进行分式的加减吗?
归纳
同分母分式相加减:同分母分式相加减,分母不变,把分子相加减,即= .
异分母分式相加减:异分母分式相加减,先通分,变为同分母分式,再加减,即.
03
新知探究
通分的概念 :
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减。化异分母的分式为同分母的分式的过程,叫作分式的通分。
03
新知探究
最简公分母的概念 :
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
03
新知探究
例3
通分:(1),,;
解: (1) 3,4,12ab中系数的最小公倍数为12,字母a的最高次幂为,字母b的最高次幂为,故公分母为12,
通分后分别为:=, =,.
如果各分母的系数都是整数时,通常取它们系数的最小公倍数作为最简公分母的系数。
03
新知探究
例3
通分:(2),,.
解: (2) x2y2=(xy)(x+y),x2+2xy+y2=(x+y) 2,x2+xy=x(x+y),
故公分母为x(x+y)2(xy).
通分后分别为:===.
当分母是多项式时,一般应先分解因式.
04
课堂练习
【知识技能类作业】必做题:
1.把分式通分时,这三个分式的分子分母依次乘 、
、 .
2.分式、的最简公分母是 ,通分为 .
04
课堂练习
【知识技能类作业】必做题:
3.填空:① ,②,括号内依次填入 , .
04
课堂练习
【知识技能类作业】选做题:
4.分式的分母经过通分后变成,那么分子应变为 .
5.当时, .
6.分式与通分后的结果是 .
,
04
课堂练习
【综合拓展类作业】
7.求出下列各组分式的最简公分母.
(1); (2);
(3); (4).
(1)解:和的最简公分母是;
(2)解:的最简公分母是;
04
课堂练习
【综合拓展类作业】
(3); (4).
(3)解:的最简公分母是;
(4)解:的最简公分母是.
05
课堂小结
如何确定分式的最简公分母:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
06
作业布置
【知识技能类作业】
1.在计算通分时,分母确定为( )
A. B. C. D.
2.只把分式中的m,n同时扩大为原来的3倍后,分式的值也不会变,则此时a的值可以是下列中的( )
A.2 B.mn C.m D.m2
B
C
06
作业布置
【知识技能类作业】
3.把分式,,通分,下列结论错误的是( )
A.最简公分母是(x-2)(x+1)2
B. =
C. =
D. =
D
06
作业布置
【综合拓展类作业】
4.甲完成一项工作需要天,乙完成这项工作要比甲多8天,设工作总量为1,写出表示甲、乙两人工作效率的式子,若两式的分母不同,则将两个式子进行通分.
解:甲的工作效率为,乙的工作效率为.
,
.
07
板书设计
同分母:
异分母:
通分:
最简公分母:
9.2.2 分式的加减(1)
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
