2024--2025学年小学毕业会考数学综合模拟试卷(2)
文档属性
| 名称 | 2024--2025学年小学毕业会考数学综合模拟试卷(2) |

|
|
| 格式 | docx | ||
| 文件大小 | 566.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024--2025学年小学毕业会考数学综合模拟试卷(2)
一、选择题
1.下面各数中,读两个零的是( )。
A.3003030 B.3030300 C.3003003 D.3300300
2.睡鼠是冬眠时间最长的动物,一般每年有5~6个月的时间处于冬眠状态。动物学家跟踪研究的一只睡鼠从2023年10月21日开始冬眠,直到2024年4月3日才出洞,这只睡鼠冬眠了( )天。
A.163 B.164 C.165 D.166
3.羚羊是世界上跑得较快的动物之一。如图表示藏羚羊的速度和叉角羚羊的速度之间的关系。已知藏羚羊的速度约是110千米/时,求叉角羚羊的速度的正确列式是( )。
A.110× B.110
C.110× D.110
4.一本书,李老师第一天读了总页数的,第二天读了余下的。哪天读得多?( )
A.第一天 B.第二天 C.一样多 D.无法确定
5.如图是一个透明的密封容器,水深6厘米。如果把它的右面作为底面平放在桌上,这时水的高度是( )厘米。
A.4 B.8 C.6 D.10
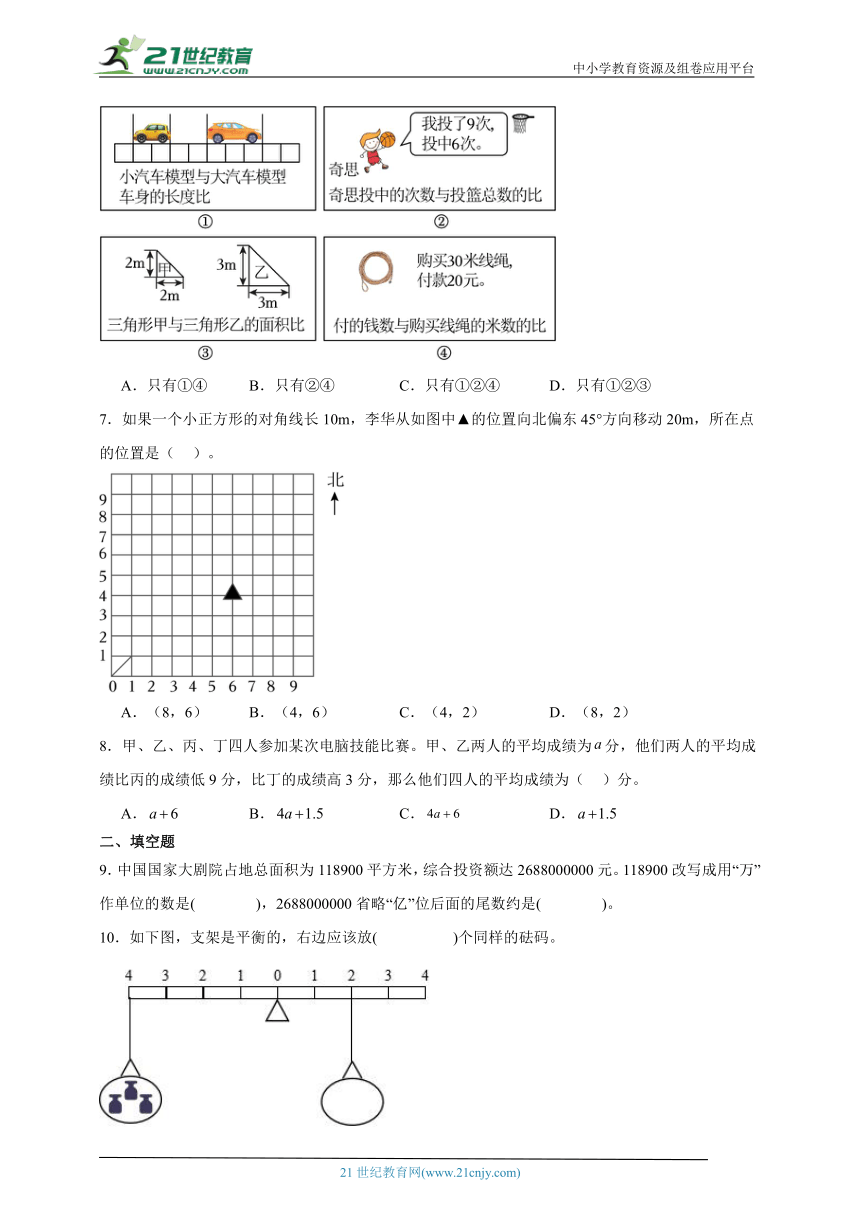
6.如图四个情境中,两个量之比可以用2∶3表示的( )。
A.只有①④ B.只有②④ C.只有①②④ D.只有①②③
7.如果一个小正方形的对角线长10m,李华从如图中▲的位置向北偏东45°方向移动20m,所在点的位置是( )。
A.(8,6) B.(4,6) C.(4,2) D.(8,2)
8.甲、乙、丙、丁四人参加某次电脑技能比赛。甲、乙两人的平均成绩为分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为( )分。
A. B. C. D.
二、填空题
9.中国国家大剧院占地总面积为118900平方米,综合投资额达2688000000元。118900改写成用“万”作单位的数是( ),2688000000省略“亿”位后面的尾数约是( )。
10.如下图,支架是平衡的,右边应该放( )个同样的砝码。
11.如果a=4b(a、b均不为0),a和b的最小公倍数是( ),a和b的最大公因数是( )。
12.3.8公顷=( )平方千米=( )平方米 时=( )分
13.“美团”被网民戏称为“国民级保姆”,这里的酒店预订简单直接。据统计,2024年五一期间与2022年同期比较“线上酒店预定超三倍,游客增加四成”,把横线上的两条信息用百分数表示分别是( )和( )。
14.张谦老师编写了一本《数学童话》,得到稿费4800元。按规定,一次稿费超过800元的部分,应该以14%的税率纳税。张老师应该缴纳税款( )元,他实际得到稿费( )元。
15.一个三角形的三条边长度和为42cm,三条边长度之比是2∶3∶2,这个三角形最长边是( )cm。按边分类,它是( )三角形。
16.外语小学制作宣传栏表彰“阅读小达人”,下图是一位同学的二寸照片尺寸,老师想按比例放大后装进宣传栏,放大后照片的宽是22cm,长是( )cm。
17.“母亲节”这天,张楠亲手为妈妈做了一个形状近似圆柱的蛋糕。蛋糕直径10cm,高8cm,这个蛋糕的体积是( )cm3。张楠想用包装纸制作一个长方体蛋糕盒,正好可以把蛋糕放进去,她至少需要准备( )cm2包装纸。(接头损耗忽略不计)
18.一辆小汽车的牌照是豫M8L○□Δ,已知○+○=□,○+□+□+5=15,Δ+Δ=○,那么牌照号码的后三位数是( )。
三、计算题
19.直接写得数。
1÷80%= 3.14×52×4= = 3.8÷10%×0.01=
= = = 3.68-0.82-0.18=
= = = =
20.脱式计算,能简算的要简算。
21.求未知数。
3.5+4.6×2=16.2 =
四、作图题
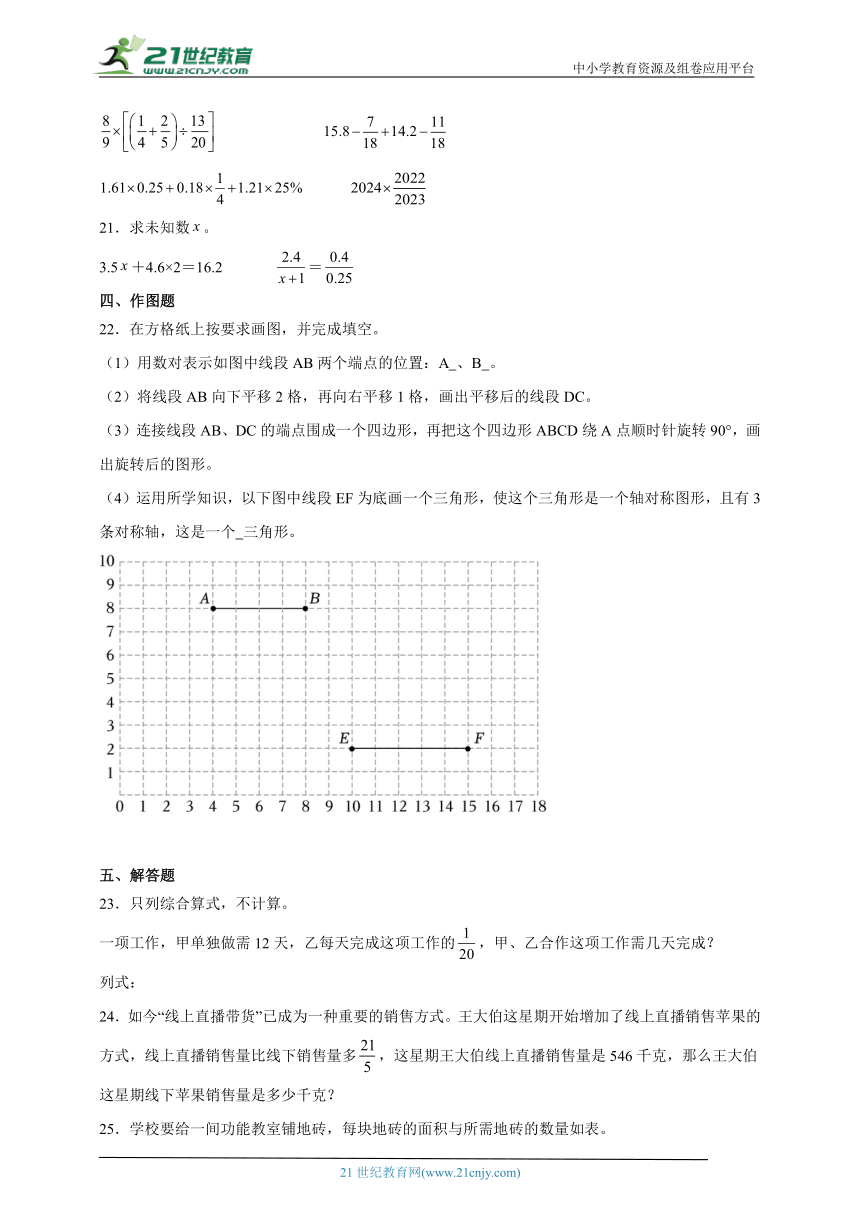
22.在方格纸上按要求画图,并完成填空。
(1)用数对表示如图中线段AB两个端点的位置:A 、B 。
(2)将线段AB向下平移2格,再向右平移1格,画出平移后的线段DC。
(3)连接线段AB、DC的端点围成一个四边形,再把这个四边形ABCD绕A点顺时针旋转90°,画出旋转后的图形。
(4)运用所学知识,以下图中线段EF为底画一个三角形,使这个三角形是一个轴对称图形,且有3条对称轴,这是一个 三角形。
五、解答题
23.只列综合算式,不计算。
一项工作,甲单独做需12天,乙每天完成这项工作的,甲、乙合作这项工作需几天完成?
列式:
24.如今“线上直播带货”已成为一种重要的销售方式。王大伯这星期开始增加了线上直播销售苹果的方式,线上直播销售量比线下销售量多,这星期王大伯线上直播销售量是546千克,那么王大伯这星期线下苹果销售量是多少千克?
25.学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
26.爸爸在网上买一件上衣,两家网店的原价都是280元。爸爸选择哪家店买更省钱?请计算说明。
A店:每满100元减30元 B店:七五折酬宾
27.一辆轿车从甲地开往乙地需要5小时,3小时后在服务区加了汽油,接着又行驶了48千米,这时轿车所行路程与剩下路程的比是7∶3,甲乙两地相距多少千米?(先画出线段图再解答)
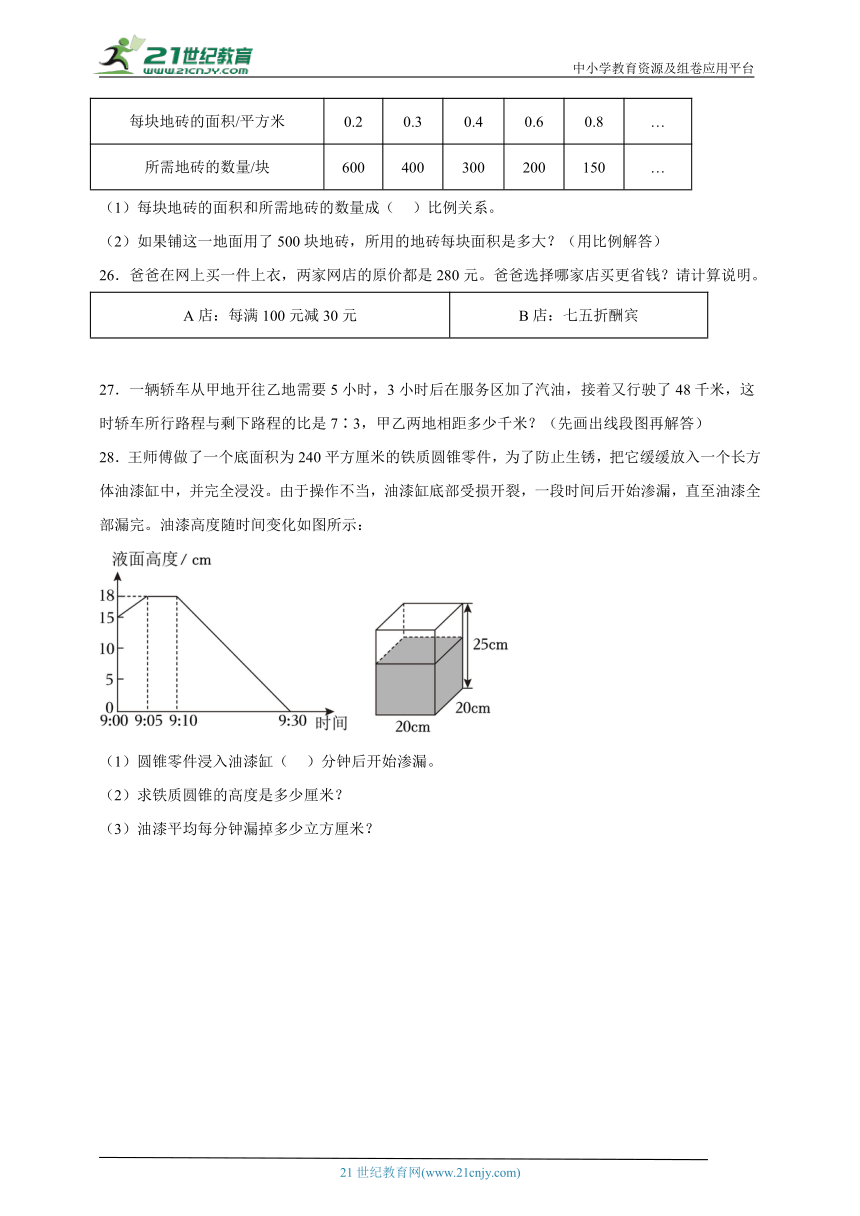
28.王师傅做了一个底面积为240平方厘米的铁质圆锥零件,为了防止生锈,把它缓缓放入一个长方体油漆缸中,并完全浸没。由于操作不当,油漆缸底部受损开裂,一段时间后开始渗漏,直至油漆全部漏完。油漆高度随时间变化如图所示:
(1)圆锥零件浸入油漆缸( )分钟后开始渗漏。
(2)求铁质圆锥的高度是多少厘米?
(3)油漆平均每分钟漏掉多少立方厘米?
参考答案
1.B
根据整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,即可读出此数,解答此题。
A.3003030读作:三百万三千零三十,读一个零,不符合题意;
B.3030300读作:三百零三万零三百,读两个零,符合题意;
C.3003003读作:三百万三千零三,读一个零,不符合题意;
D.3300300读作:三百三十万零三百,读一个零,不符合题意。
故答案为:B
2.C
一年一共有12个月,其中1月、3月、5月、7月、8月、10月、12月是大月,每个月有31天,4月、6月、9月、11月是小月,每个月有30天,公历年份是4的倍数的一般都是闰年,但公历年份是100的倍数时,必须是400的倍数才是闰年,闰年的2月有29天,平年的2月有28天,开始冬眠那一天需要计算在内,出洞那一天不属于冬眠时间需要去掉,据此解答。
2024÷4=506
则2024年是闰年,2月有29天。
31-21+1+30+31+31+29+31+(3-1)
=31-21+1+30+31+31+29+31+2
=11+30+31+31+29+31+2
=41+31+31+29+31+2
=72+31+29+31+2
=103+29+31+2
=132+31+2
=163+2
=165(天)
所以,这只睡鼠冬眠了165天。
故答案为:C
3.C
由题意可知,把藏羚羊的速度看作单位“1”,角羚羊的速度是藏羚羊的,根据求一个数的几分之几是多少,用乘法计算,据此解答。
110×(1-)
(千米/时)
叉角羚羊的速度的正确列式是110×(1-)。
故答案为:C
4.C
由题意可知,是把总页数看作单位“1”,第一天读后余下的是总页数的,是把余下的页数看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,可用求第二天看了总页数的几分之几,再比较大小,即可得解。
(1-)×
=×
=
=
两天读得一样多。
故答案为:C
5.A
根据长方体体积公式:体积=长×宽×高,代入数据,求出长是8厘米,宽是4厘米,高是6厘米水的体积;由于体积不变,再用水的体积除以长是12厘米,宽是4厘米的面的面积,即可解答。
8×4×6÷(12×4)
=8×4×6÷48
=32×6÷48
=192÷48
=4(厘米)
水深6厘米。如果把它的右面作为底面平放在桌上,这时水的高度是4厘米。
故答案为:A
6.C
①图中小汽车模型的身长是2,大汽车模型的身长是3,根据比的意义写出两车的车身长度比。
②奇思投了9次,投中6次,根据比的意义写出投中的次数与投篮总数的比,并化简比。
③根据三角形的面积=底×高÷2,求出三角形甲、乙的面积,根据比的意义写出甲、乙的面积比。
④已知购买30米线绳,付了20元,根据比的意义写出付的钱数与购买线绳的米数的比,并化简比。
从中找出两个量之比可以用2∶3表示的情境。
①小汽车模型与大汽车模型身长的比是2∶3;
②奇思投中次数与投篮总数的比是6∶9=(6÷3)∶(9÷3)=2∶3;
③三角形甲与三角形乙的面积比是(2×2÷2)∶(3×3÷2)=4∶9;
④付的钱数与购买线绳的米数的比是20∶30=(20÷10)∶(30÷10)=2∶3;
综上所述,两个量之比可以用2∶3表示的是①②④。
故答案为:C
7.A
根据小正方形对角线长度和移动距离确定移动的格数,再结合方向(北偏东45°)和数对的知识(第一个数字表示列,第二个数字表示行)来确定位置。
如图:
如果一个小正方形的对角线长10m,李华从如图中▲的位置向北偏东45°方向移动20m,所在点的位置是(8,6)。
故答案为:A
8.D
由已知条件先求出丙的成绩为,再求出丁的成绩,求出四人成绩和,用所得和除以4,结果即为总平均数。
丙:
丁:
四人成绩和:
四人平均成绩:
故答案为:D
本题的关键是根据总的平均成绩=总成绩÷总人数,进行解答。
9. 11.89万 27亿/2700000000
改写成用“万”作单位的数,就是在万位的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;省略亿位后面的尾数,就是四舍五入到亿位,看千万位上的数进行四舍五入,再在数的后面写上“亿”字,据此解答。
118900=11.89万
2688000000≈2700000000=27亿
故118900改写成用“万”作单位的数是11.89万,2688000000省略“亿”位后面的尾数约是27亿。
10.6
根据左边砝码数量×砝码位置到中间的距离=右边砝码数量×砝码位置到中间的距离;左边3个砝码,到中间的距离是4,右边到中间的距离是2,求出砝码数量,列反比例,进行解答。
解:设右边应放x个同样的砝码。
2x=3×4
2x=12
x=12÷2
x=6
解答本题的关键是先判断题中的两种相关联的量成哪种比例,然后找准对应量,列式解答即可。
11. a b
求两数的最大公因数和最小公倍数,先看两个数之间的关系,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积;两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
由a=4b,得:a÷b=4,即a和b是倍数关系,所以a和b的最小公倍数是a,最大公因数是b。
熟练掌握求两个数的最大公因数和最小公倍数的方法是解题的关键。
12. 0.038 38000 105
本题考查单位换算,1平方千米=100公顷,1公顷=10000平方米,1时=60分,大单位换算为小单位乘进率;小单位换算为大单位除以进率,分别根据进率关系推导即可。
①公顷换算为平方千米,小单位换算为大单位除以进率100,3.8÷100=0.038,所以3.8公顷=0.038平方千米;
②公顷换算为平方米,大单位换算为小单位乘进率10000,3.8×10000=38000,所以3.8公顷=38000平方米;
③时换算为分,大单位换算为小单位乘进率60,×60=×60=105,所以时=105分。
13. 300% 40%
倍数表示一个数是另一个数的几倍,可以转化为比例关系用百分数的形式表示;
成数表示一个数是另一个数的十分之几,几成即十分之几、百分之几十。
根据倍数关系可知,三倍意味着是原来的3倍,将其转化为百分数,把倍数关系转化为比例关系,用3÷1×100%=300%,所以三倍用百分数表示是300%;
根据成数的含义可知:四成即十分之四,也就是百分之四十,用百分数表示就是40%。
14. 560 4240
本题考查百分数的应用,税率问题。首先要确定需要纳税的部分:稿费超过800元的部分才纳税,张老师的稿费是4800元,超过800元的部分是4800-800=4000元,然后根据“税款=应纳税部分×税率”计算出应缴纳的税款,最后用总的稿费减去缴纳的税款,就是实际得到的稿费。
4800-800=4000(元)
4000×14%=560(元)
张老师应该缴纳税款560元。
4800-560=4240(元)
所以张老师实际得到稿费4240元。
15. 18 等腰
已知三角形的三条边长度和为42cm,三条边长度之比是2∶3∶2,那么最长的边占三条边长度和的,根据求一个数的几分之几是多少,用三条边的长度和乘,求出这个三角形的最长边;再根据三角形按边的分类,确定这个三角形的类型。
42×
=42×
=18(cm)
因为三条边长度之比是2∶3∶2可知,这个三角形有两条边相等,所以它是等腰三角形。
填空如下:
这个三角形最长边是(18)cm。按边分类,它是(等腰)三角形。
16.32
因为照片按比例放大,所以放大前后长和宽的比值是相等的,我们可以据此列出比例,再根据比例的基本性质(两个内项之积等于两个外项之积)来求解。
解:设放大后照片的长是x厘米。
所以放大后照片的长是32厘米。
17. 628 520
①由题可知:蛋糕形状近似圆柱,求蛋糕的体积就是计算圆柱的体积,已知底面直径10厘米计算出半径,根据公式计算体积即可;
②要让长方体蛋糕盒正好装下圆柱蛋糕,长方体的长和宽得和圆柱底面直径一样,是10厘米,高得和圆柱的高一样,是8厘米,计算包装纸的大小就是计算长方体的表面积,根据公式长方体的表面积=(长×宽+长×高+宽×高)×2计算出表面积即可;
①3.14×(10÷2)2×8
=3.14×25×8
=78.5×8
=628(立方厘米)
所以这个蛋糕的体积是628立方厘米。
②(10×10+10×8+10×8)×2
=(100+80+80)×2
=260×2
=520(平方厘米)
所以至少需要520平方厘米的包装纸。
18.241
已知○+○=□,把○+□+□+5=15中的□用2个○代替,则算式变成5○+5=15,进而求出○的值;
把○的值代入○+○=□中,求出□的值;把○的值代入Δ+Δ=○中,求出Δ的值;
据此得出牌照“豫M8L○□Δ”后面的三位数。
因为○+○=□,那么:
○+□+□+5=15
○+○+○+○+○+5=15
5○+5=15
5○=15-5
5○=10
○=10÷5
○=2
□=○+○=2+2=4
Δ+Δ=○,则Δ=○÷2=2÷2=1
所以,牌照是豫M8L○□Δ的后三位数是241。
19.1.25;314;;0.38;
;;;2.68;
1;2;0;49
略
20.;29;
0.75;
(1)先算小括号里面的加法,再算中括号里面的除法,最后算中括号外面的乘法;
(2)先交换“”和“”的位置,然后根据加法减法的性质a-b-c=a-(b+c)把变成,再按顺序计算;
(3)先把、25%变成0.25,然后根据乘法分配律a×c+b×c=(a+b)×c把变成,再按顺序计算;
(4)先把2024拆成2023+1,然后根据乘法分配律计算(a+b)×c=a×c+b×c把变成,再按顺序计算。
(1)
=
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=
(4)
=
=
=
=
21.=2;=
(1)先把方程化简成3.5+9.2=16.2,然后根据等式的性质解方程,方程两边先同时减去9.2,再同时除以3.5,求出方程的解;
(2)先根据比例的基本性质把比例方程改写成0.4(+1)=2.4×0.25,然后把方程化简成0.4+0.4=0.6,再根据等式的性质解方程,方程两边先同时减去0.4,再同时除以0.4,求出方程的解。
(1)3.5+4.6×2=16.2
解:3.5+9.2=16.2
3.5+9.2-9.2=16.2-9.2
3.5=7
3.5÷3.5=7÷3.5
=2
(2)=
解:0.4(+1)=2.4×0.25
0.4+0.4=0.6
0.4+0.4-0.4=0.6-0.4
0.4=0.2
0.4÷0.4=0.2÷0.4
=
22.(1)(4,8);(8,8)
(2)见详解
(3)见详解
(4)图见详解;等边
(1)在方格纸中,数对的前一个数表示列,后一个数表示行。据此数出A、B两点分别在第几列、第几行即可解答;
(2)将线段AB的A点和B点分别向下平移2格再向右平移1格,得到新的点C和D,然后连接DC,完成线段的平移;
(3)根据旋转的特征,A点不动,梯形ABCD绕点A顺时针方向旋转90°,据此画图即可;
(4)以线段EF为底,要画出一个有3条对称轴的轴对称图形,这个三角形是等边三角形。因为等边三角形有3条对称轴。
(1)用数对表示如图中线段AB两个端点的位置:A (4,8)、B (8,8)。
(2)将线段AB向下平移2格,再向右平移1格,画出平移后的线段DC。如图:
(3)连接线段AB、DC的端点围成一个四边形,再把这个四边形ABCD绕A点顺时针旋转90°,画出旋转后的图形。如图:
(4)运用所学知识,以下图中线段EF为底画一个三角形,使这个三角形是一个轴对称图形,且有3条对称轴,这是一个等边三角形。如图:
23.1÷()
把这项工作看作单位“1”,甲单独做12天完成,每天完成这项工作的;甲乙合作一天就可以完成这项工作的(),根据工作时间=工作总量÷工作效率,即可列式解答。
根据分析可得:
1÷()
=1÷
=1×
=7.5(天)
答:甲、乙合作这项工作需7.5天完成。
24.105千克
把线下销售量看作单位“1”,线上直播销售量比线下销售量多,则线上直播销售量是线下销售量的(1+),根据已知一个数比另一个数多几分之几是多少,求这个数,用除法计算,据此解答。
546÷(1+)
=546÷
=546×
=105(千克)
答:王大伯这星期线下苹果销售量是105千克。
25.(1)反
(2)0.24平方米
(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
(2)因为功能教室地面的总面积是一定的,所以每块地砖的面积和所需地砖的数量成反比例关系,我们可以据此列比例式来求解;设所用的地砖每块面积是x平方米。因为地面总面积一定,每块地砖面积和所需地砖数量成反比例,所以可列方程500x= 0.2×600。
(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=…=120(一定),乘积一定,所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)如果铺这一地面用了500块地砖,设所用的地砖每块面积是x平方米。
500x=0.2×600
500x=120
x=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
26.B店;计算见详解
A店每满100元减30元,用除法求出280里面有几个100,即可减几个30元,求出实际花的钱数;B店打七五折销售,即按原价的75%出售,根据百分数乘法的意义:求一个数的百分之几是多少,用乘法解答,据此用乘法求出打折后的价钱;再比较即可。
A店:280÷100=2(个)……80(元)
280-30×2
=280-60
=220(元)
B点:280×75%=210(元)
220>210
答:爸爸选择B店买更省钱。
27.线段图见详解;480千米
这道题可把全程看成单位“1”,轿车从甲地开往乙地需要5小时,可知每小时行驶了全程的,3小时则行驶了全程的;又行驶了48千米,这时轿车所行路程与剩下路程的比是7∶3,可知这时已行驶了全程的,用可算出48千米所对应的分率,即可算出全程。
(千米)
答:甲乙两地相距480千米。
28.(1)10
(2)15厘米
(3)300立方厘米
(1)从液面高度与时间的关系图中可知,9:00开始往长方体油漆缸里放入圆锥零件,9:00~9:05,液面高度上升;9:05~9:10,液面高度不变;9:10~9:30,液面高度下降。
由此可知,9:10液面开始渗漏,用开始渗漏的时刻减去放入圆锥零件的时刻,即可求出圆锥零件浸入油漆缸几分钟后开始渗漏。
(2)把一个铁质圆锥零件完全浸没在长方体油漆缸中,液面高度由15厘米上升到18厘米,上升了(18-15)厘米;液面上升部分的体积就是这个圆锥零件的体积;
先根据长方体的体积=长×宽×高,求出液面上升部分的体积,即圆锥零件的体积;
再根据圆锥的体积公式V=Sh可知,圆锥的高h=3V÷S,据此求出圆锥零件的高度。
(3)从图中可知,9:10油漆开始渗漏,9:30油漆全部漏完,用时20分钟;
长方体油漆缸长20厘米、宽20厘米、液面高15厘米,根据长方体的体积(容积)=长×宽×高,求出油漆的体积;
用油漆的体积除以渗漏的时间,即可求出油漆平均每分钟漏掉的体积。
(1)9时10分-9时=10(分钟)
圆锥零件浸入油漆缸(10)分钟后开始渗漏。
(2)液面上升部分的体积:
20×20×(18-15)
=20×20×3
=1200(立方厘米)
圆锥的高:
1200×3÷240
=3600÷240
=15(厘米)
答:铁质圆锥的高度是15厘米。
(3)9时30分-9时10分=20(分钟)
20×20×15
=400×15
=6000(立方厘米)
6000÷20=300(立方厘米)
答:油漆平均每分钟漏掉300立方厘米。
从液面高度与时间的关系图中获取信息,如:放入圆锥零件后液面上升的高,每段时间液面的变化情况等;灵活运用长方体的体积公式、圆锥的体积公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年小学毕业会考数学综合模拟试卷(2)
一、选择题
1.下面各数中,读两个零的是( )。
A.3003030 B.3030300 C.3003003 D.3300300
2.睡鼠是冬眠时间最长的动物,一般每年有5~6个月的时间处于冬眠状态。动物学家跟踪研究的一只睡鼠从2023年10月21日开始冬眠,直到2024年4月3日才出洞,这只睡鼠冬眠了( )天。
A.163 B.164 C.165 D.166
3.羚羊是世界上跑得较快的动物之一。如图表示藏羚羊的速度和叉角羚羊的速度之间的关系。已知藏羚羊的速度约是110千米/时,求叉角羚羊的速度的正确列式是( )。
A.110× B.110
C.110× D.110
4.一本书,李老师第一天读了总页数的,第二天读了余下的。哪天读得多?( )
A.第一天 B.第二天 C.一样多 D.无法确定
5.如图是一个透明的密封容器,水深6厘米。如果把它的右面作为底面平放在桌上,这时水的高度是( )厘米。
A.4 B.8 C.6 D.10
6.如图四个情境中,两个量之比可以用2∶3表示的( )。
A.只有①④ B.只有②④ C.只有①②④ D.只有①②③
7.如果一个小正方形的对角线长10m,李华从如图中▲的位置向北偏东45°方向移动20m,所在点的位置是( )。
A.(8,6) B.(4,6) C.(4,2) D.(8,2)
8.甲、乙、丙、丁四人参加某次电脑技能比赛。甲、乙两人的平均成绩为分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为( )分。
A. B. C. D.
二、填空题
9.中国国家大剧院占地总面积为118900平方米,综合投资额达2688000000元。118900改写成用“万”作单位的数是( ),2688000000省略“亿”位后面的尾数约是( )。
10.如下图,支架是平衡的,右边应该放( )个同样的砝码。
11.如果a=4b(a、b均不为0),a和b的最小公倍数是( ),a和b的最大公因数是( )。
12.3.8公顷=( )平方千米=( )平方米 时=( )分
13.“美团”被网民戏称为“国民级保姆”,这里的酒店预订简单直接。据统计,2024年五一期间与2022年同期比较“线上酒店预定超三倍,游客增加四成”,把横线上的两条信息用百分数表示分别是( )和( )。
14.张谦老师编写了一本《数学童话》,得到稿费4800元。按规定,一次稿费超过800元的部分,应该以14%的税率纳税。张老师应该缴纳税款( )元,他实际得到稿费( )元。
15.一个三角形的三条边长度和为42cm,三条边长度之比是2∶3∶2,这个三角形最长边是( )cm。按边分类,它是( )三角形。
16.外语小学制作宣传栏表彰“阅读小达人”,下图是一位同学的二寸照片尺寸,老师想按比例放大后装进宣传栏,放大后照片的宽是22cm,长是( )cm。
17.“母亲节”这天,张楠亲手为妈妈做了一个形状近似圆柱的蛋糕。蛋糕直径10cm,高8cm,这个蛋糕的体积是( )cm3。张楠想用包装纸制作一个长方体蛋糕盒,正好可以把蛋糕放进去,她至少需要准备( )cm2包装纸。(接头损耗忽略不计)
18.一辆小汽车的牌照是豫M8L○□Δ,已知○+○=□,○+□+□+5=15,Δ+Δ=○,那么牌照号码的后三位数是( )。
三、计算题
19.直接写得数。
1÷80%= 3.14×52×4= = 3.8÷10%×0.01=
= = = 3.68-0.82-0.18=
= = = =
20.脱式计算,能简算的要简算。
21.求未知数。
3.5+4.6×2=16.2 =
四、作图题
22.在方格纸上按要求画图,并完成填空。
(1)用数对表示如图中线段AB两个端点的位置:A 、B 。
(2)将线段AB向下平移2格,再向右平移1格,画出平移后的线段DC。
(3)连接线段AB、DC的端点围成一个四边形,再把这个四边形ABCD绕A点顺时针旋转90°,画出旋转后的图形。
(4)运用所学知识,以下图中线段EF为底画一个三角形,使这个三角形是一个轴对称图形,且有3条对称轴,这是一个 三角形。
五、解答题
23.只列综合算式,不计算。
一项工作,甲单独做需12天,乙每天完成这项工作的,甲、乙合作这项工作需几天完成?
列式:
24.如今“线上直播带货”已成为一种重要的销售方式。王大伯这星期开始增加了线上直播销售苹果的方式,线上直播销售量比线下销售量多,这星期王大伯线上直播销售量是546千克,那么王大伯这星期线下苹果销售量是多少千克?
25.学校要给一间功能教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/平方米 0.2 0.3 0.4 0.6 0.8 …
所需地砖的数量/块 600 400 300 200 150 …
(1)每块地砖的面积和所需地砖的数量成( )比例关系。
(2)如果铺这一地面用了500块地砖,所用的地砖每块面积是多大?(用比例解答)
26.爸爸在网上买一件上衣,两家网店的原价都是280元。爸爸选择哪家店买更省钱?请计算说明。
A店:每满100元减30元 B店:七五折酬宾
27.一辆轿车从甲地开往乙地需要5小时,3小时后在服务区加了汽油,接着又行驶了48千米,这时轿车所行路程与剩下路程的比是7∶3,甲乙两地相距多少千米?(先画出线段图再解答)
28.王师傅做了一个底面积为240平方厘米的铁质圆锥零件,为了防止生锈,把它缓缓放入一个长方体油漆缸中,并完全浸没。由于操作不当,油漆缸底部受损开裂,一段时间后开始渗漏,直至油漆全部漏完。油漆高度随时间变化如图所示:
(1)圆锥零件浸入油漆缸( )分钟后开始渗漏。
(2)求铁质圆锥的高度是多少厘米?
(3)油漆平均每分钟漏掉多少立方厘米?
参考答案
1.B
根据整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,即可读出此数,解答此题。
A.3003030读作:三百万三千零三十,读一个零,不符合题意;
B.3030300读作:三百零三万零三百,读两个零,符合题意;
C.3003003读作:三百万三千零三,读一个零,不符合题意;
D.3300300读作:三百三十万零三百,读一个零,不符合题意。
故答案为:B
2.C
一年一共有12个月,其中1月、3月、5月、7月、8月、10月、12月是大月,每个月有31天,4月、6月、9月、11月是小月,每个月有30天,公历年份是4的倍数的一般都是闰年,但公历年份是100的倍数时,必须是400的倍数才是闰年,闰年的2月有29天,平年的2月有28天,开始冬眠那一天需要计算在内,出洞那一天不属于冬眠时间需要去掉,据此解答。
2024÷4=506
则2024年是闰年,2月有29天。
31-21+1+30+31+31+29+31+(3-1)
=31-21+1+30+31+31+29+31+2
=11+30+31+31+29+31+2
=41+31+31+29+31+2
=72+31+29+31+2
=103+29+31+2
=132+31+2
=163+2
=165(天)
所以,这只睡鼠冬眠了165天。
故答案为:C
3.C
由题意可知,把藏羚羊的速度看作单位“1”,角羚羊的速度是藏羚羊的,根据求一个数的几分之几是多少,用乘法计算,据此解答。
110×(1-)
(千米/时)
叉角羚羊的速度的正确列式是110×(1-)。
故答案为:C
4.C
由题意可知,是把总页数看作单位“1”,第一天读后余下的是总页数的,是把余下的页数看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,可用求第二天看了总页数的几分之几,再比较大小,即可得解。
(1-)×
=×
=
=
两天读得一样多。
故答案为:C
5.A
根据长方体体积公式:体积=长×宽×高,代入数据,求出长是8厘米,宽是4厘米,高是6厘米水的体积;由于体积不变,再用水的体积除以长是12厘米,宽是4厘米的面的面积,即可解答。
8×4×6÷(12×4)
=8×4×6÷48
=32×6÷48
=192÷48
=4(厘米)
水深6厘米。如果把它的右面作为底面平放在桌上,这时水的高度是4厘米。
故答案为:A
6.C
①图中小汽车模型的身长是2,大汽车模型的身长是3,根据比的意义写出两车的车身长度比。
②奇思投了9次,投中6次,根据比的意义写出投中的次数与投篮总数的比,并化简比。
③根据三角形的面积=底×高÷2,求出三角形甲、乙的面积,根据比的意义写出甲、乙的面积比。
④已知购买30米线绳,付了20元,根据比的意义写出付的钱数与购买线绳的米数的比,并化简比。
从中找出两个量之比可以用2∶3表示的情境。
①小汽车模型与大汽车模型身长的比是2∶3;
②奇思投中次数与投篮总数的比是6∶9=(6÷3)∶(9÷3)=2∶3;
③三角形甲与三角形乙的面积比是(2×2÷2)∶(3×3÷2)=4∶9;
④付的钱数与购买线绳的米数的比是20∶30=(20÷10)∶(30÷10)=2∶3;
综上所述,两个量之比可以用2∶3表示的是①②④。
故答案为:C
7.A
根据小正方形对角线长度和移动距离确定移动的格数,再结合方向(北偏东45°)和数对的知识(第一个数字表示列,第二个数字表示行)来确定位置。
如图:
如果一个小正方形的对角线长10m,李华从如图中▲的位置向北偏东45°方向移动20m,所在点的位置是(8,6)。
故答案为:A
8.D
由已知条件先求出丙的成绩为,再求出丁的成绩,求出四人成绩和,用所得和除以4,结果即为总平均数。
丙:
丁:
四人成绩和:
四人平均成绩:
故答案为:D
本题的关键是根据总的平均成绩=总成绩÷总人数,进行解答。
9. 11.89万 27亿/2700000000
改写成用“万”作单位的数,就是在万位的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;省略亿位后面的尾数,就是四舍五入到亿位,看千万位上的数进行四舍五入,再在数的后面写上“亿”字,据此解答。
118900=11.89万
2688000000≈2700000000=27亿
故118900改写成用“万”作单位的数是11.89万,2688000000省略“亿”位后面的尾数约是27亿。
10.6
根据左边砝码数量×砝码位置到中间的距离=右边砝码数量×砝码位置到中间的距离;左边3个砝码,到中间的距离是4,右边到中间的距离是2,求出砝码数量,列反比例,进行解答。
解:设右边应放x个同样的砝码。
2x=3×4
2x=12
x=12÷2
x=6
解答本题的关键是先判断题中的两种相关联的量成哪种比例,然后找准对应量,列式解答即可。
11. a b
求两数的最大公因数和最小公倍数,先看两个数之间的关系,两个数互质,则最大公因数是1,最小公倍数就是这两个数的乘积;两个数为倍数关系,则最大公因数是较小的数,最小公倍数为较大的数。
由a=4b,得:a÷b=4,即a和b是倍数关系,所以a和b的最小公倍数是a,最大公因数是b。
熟练掌握求两个数的最大公因数和最小公倍数的方法是解题的关键。
12. 0.038 38000 105
本题考查单位换算,1平方千米=100公顷,1公顷=10000平方米,1时=60分,大单位换算为小单位乘进率;小单位换算为大单位除以进率,分别根据进率关系推导即可。
①公顷换算为平方千米,小单位换算为大单位除以进率100,3.8÷100=0.038,所以3.8公顷=0.038平方千米;
②公顷换算为平方米,大单位换算为小单位乘进率10000,3.8×10000=38000,所以3.8公顷=38000平方米;
③时换算为分,大单位换算为小单位乘进率60,×60=×60=105,所以时=105分。
13. 300% 40%
倍数表示一个数是另一个数的几倍,可以转化为比例关系用百分数的形式表示;
成数表示一个数是另一个数的十分之几,几成即十分之几、百分之几十。
根据倍数关系可知,三倍意味着是原来的3倍,将其转化为百分数,把倍数关系转化为比例关系,用3÷1×100%=300%,所以三倍用百分数表示是300%;
根据成数的含义可知:四成即十分之四,也就是百分之四十,用百分数表示就是40%。
14. 560 4240
本题考查百分数的应用,税率问题。首先要确定需要纳税的部分:稿费超过800元的部分才纳税,张老师的稿费是4800元,超过800元的部分是4800-800=4000元,然后根据“税款=应纳税部分×税率”计算出应缴纳的税款,最后用总的稿费减去缴纳的税款,就是实际得到的稿费。
4800-800=4000(元)
4000×14%=560(元)
张老师应该缴纳税款560元。
4800-560=4240(元)
所以张老师实际得到稿费4240元。
15. 18 等腰
已知三角形的三条边长度和为42cm,三条边长度之比是2∶3∶2,那么最长的边占三条边长度和的,根据求一个数的几分之几是多少,用三条边的长度和乘,求出这个三角形的最长边;再根据三角形按边的分类,确定这个三角形的类型。
42×
=42×
=18(cm)
因为三条边长度之比是2∶3∶2可知,这个三角形有两条边相等,所以它是等腰三角形。
填空如下:
这个三角形最长边是(18)cm。按边分类,它是(等腰)三角形。
16.32
因为照片按比例放大,所以放大前后长和宽的比值是相等的,我们可以据此列出比例,再根据比例的基本性质(两个内项之积等于两个外项之积)来求解。
解:设放大后照片的长是x厘米。
所以放大后照片的长是32厘米。
17. 628 520
①由题可知:蛋糕形状近似圆柱,求蛋糕的体积就是计算圆柱的体积,已知底面直径10厘米计算出半径,根据公式计算体积即可;
②要让长方体蛋糕盒正好装下圆柱蛋糕,长方体的长和宽得和圆柱底面直径一样,是10厘米,高得和圆柱的高一样,是8厘米,计算包装纸的大小就是计算长方体的表面积,根据公式长方体的表面积=(长×宽+长×高+宽×高)×2计算出表面积即可;
①3.14×(10÷2)2×8
=3.14×25×8
=78.5×8
=628(立方厘米)
所以这个蛋糕的体积是628立方厘米。
②(10×10+10×8+10×8)×2
=(100+80+80)×2
=260×2
=520(平方厘米)
所以至少需要520平方厘米的包装纸。
18.241
已知○+○=□,把○+□+□+5=15中的□用2个○代替,则算式变成5○+5=15,进而求出○的值;
把○的值代入○+○=□中,求出□的值;把○的值代入Δ+Δ=○中,求出Δ的值;
据此得出牌照“豫M8L○□Δ”后面的三位数。
因为○+○=□,那么:
○+□+□+5=15
○+○+○+○+○+5=15
5○+5=15
5○=15-5
5○=10
○=10÷5
○=2
□=○+○=2+2=4
Δ+Δ=○,则Δ=○÷2=2÷2=1
所以,牌照是豫M8L○□Δ的后三位数是241。
19.1.25;314;;0.38;
;;;2.68;
1;2;0;49
略
20.;29;
0.75;
(1)先算小括号里面的加法,再算中括号里面的除法,最后算中括号外面的乘法;
(2)先交换“”和“”的位置,然后根据加法减法的性质a-b-c=a-(b+c)把变成,再按顺序计算;
(3)先把、25%变成0.25,然后根据乘法分配律a×c+b×c=(a+b)×c把变成,再按顺序计算;
(4)先把2024拆成2023+1,然后根据乘法分配律计算(a+b)×c=a×c+b×c把变成,再按顺序计算。
(1)
=
=
=
=
=
(2)
=
=
=
=
(3)
=
=
=
=
(4)
=
=
=
=
21.=2;=
(1)先把方程化简成3.5+9.2=16.2,然后根据等式的性质解方程,方程两边先同时减去9.2,再同时除以3.5,求出方程的解;
(2)先根据比例的基本性质把比例方程改写成0.4(+1)=2.4×0.25,然后把方程化简成0.4+0.4=0.6,再根据等式的性质解方程,方程两边先同时减去0.4,再同时除以0.4,求出方程的解。
(1)3.5+4.6×2=16.2
解:3.5+9.2=16.2
3.5+9.2-9.2=16.2-9.2
3.5=7
3.5÷3.5=7÷3.5
=2
(2)=
解:0.4(+1)=2.4×0.25
0.4+0.4=0.6
0.4+0.4-0.4=0.6-0.4
0.4=0.2
0.4÷0.4=0.2÷0.4
=
22.(1)(4,8);(8,8)
(2)见详解
(3)见详解
(4)图见详解;等边
(1)在方格纸中,数对的前一个数表示列,后一个数表示行。据此数出A、B两点分别在第几列、第几行即可解答;
(2)将线段AB的A点和B点分别向下平移2格再向右平移1格,得到新的点C和D,然后连接DC,完成线段的平移;
(3)根据旋转的特征,A点不动,梯形ABCD绕点A顺时针方向旋转90°,据此画图即可;
(4)以线段EF为底,要画出一个有3条对称轴的轴对称图形,这个三角形是等边三角形。因为等边三角形有3条对称轴。
(1)用数对表示如图中线段AB两个端点的位置:A (4,8)、B (8,8)。
(2)将线段AB向下平移2格,再向右平移1格,画出平移后的线段DC。如图:
(3)连接线段AB、DC的端点围成一个四边形,再把这个四边形ABCD绕A点顺时针旋转90°,画出旋转后的图形。如图:
(4)运用所学知识,以下图中线段EF为底画一个三角形,使这个三角形是一个轴对称图形,且有3条对称轴,这是一个等边三角形。如图:
23.1÷()
把这项工作看作单位“1”,甲单独做12天完成,每天完成这项工作的;甲乙合作一天就可以完成这项工作的(),根据工作时间=工作总量÷工作效率,即可列式解答。
根据分析可得:
1÷()
=1÷
=1×
=7.5(天)
答:甲、乙合作这项工作需7.5天完成。
24.105千克
把线下销售量看作单位“1”,线上直播销售量比线下销售量多,则线上直播销售量是线下销售量的(1+),根据已知一个数比另一个数多几分之几是多少,求这个数,用除法计算,据此解答。
546÷(1+)
=546÷
=546×
=105(千克)
答:王大伯这星期线下苹果销售量是105千克。
25.(1)反
(2)0.24平方米
(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此判断。
(2)因为功能教室地面的总面积是一定的,所以每块地砖的面积和所需地砖的数量成反比例关系,我们可以据此列比例式来求解;设所用的地砖每块面积是x平方米。因为地面总面积一定,每块地砖面积和所需地砖数量成反比例,所以可列方程500x= 0.2×600。
(1)0.2×600=0.3×400=0.4×300=0.6×200=0.8×150=…=120(一定),乘积一定,所以每块地砖的面积和所需地砖的数量成反比例关系。
(2)如果铺这一地面用了500块地砖,设所用的地砖每块面积是x平方米。
500x=0.2×600
500x=120
x=120÷500
x=0.24
答:所用的地砖每块面积是0.24平方米。
26.B店;计算见详解
A店每满100元减30元,用除法求出280里面有几个100,即可减几个30元,求出实际花的钱数;B店打七五折销售,即按原价的75%出售,根据百分数乘法的意义:求一个数的百分之几是多少,用乘法解答,据此用乘法求出打折后的价钱;再比较即可。
A店:280÷100=2(个)……80(元)
280-30×2
=280-60
=220(元)
B点:280×75%=210(元)
220>210
答:爸爸选择B店买更省钱。
27.线段图见详解;480千米
这道题可把全程看成单位“1”,轿车从甲地开往乙地需要5小时,可知每小时行驶了全程的,3小时则行驶了全程的;又行驶了48千米,这时轿车所行路程与剩下路程的比是7∶3,可知这时已行驶了全程的,用可算出48千米所对应的分率,即可算出全程。
(千米)
答:甲乙两地相距480千米。
28.(1)10
(2)15厘米
(3)300立方厘米
(1)从液面高度与时间的关系图中可知,9:00开始往长方体油漆缸里放入圆锥零件,9:00~9:05,液面高度上升;9:05~9:10,液面高度不变;9:10~9:30,液面高度下降。
由此可知,9:10液面开始渗漏,用开始渗漏的时刻减去放入圆锥零件的时刻,即可求出圆锥零件浸入油漆缸几分钟后开始渗漏。
(2)把一个铁质圆锥零件完全浸没在长方体油漆缸中,液面高度由15厘米上升到18厘米,上升了(18-15)厘米;液面上升部分的体积就是这个圆锥零件的体积;
先根据长方体的体积=长×宽×高,求出液面上升部分的体积,即圆锥零件的体积;
再根据圆锥的体积公式V=Sh可知,圆锥的高h=3V÷S,据此求出圆锥零件的高度。
(3)从图中可知,9:10油漆开始渗漏,9:30油漆全部漏完,用时20分钟;
长方体油漆缸长20厘米、宽20厘米、液面高15厘米,根据长方体的体积(容积)=长×宽×高,求出油漆的体积;
用油漆的体积除以渗漏的时间,即可求出油漆平均每分钟漏掉的体积。
(1)9时10分-9时=10(分钟)
圆锥零件浸入油漆缸(10)分钟后开始渗漏。
(2)液面上升部分的体积:
20×20×(18-15)
=20×20×3
=1200(立方厘米)
圆锥的高:
1200×3÷240
=3600÷240
=15(厘米)
答:铁质圆锥的高度是15厘米。
(3)9时30分-9时10分=20(分钟)
20×20×15
=400×15
=6000(立方厘米)
6000÷20=300(立方厘米)
答:油漆平均每分钟漏掉300立方厘米。
从液面高度与时间的关系图中获取信息,如:放入圆锥零件后液面上升的高,每段时间液面的变化情况等;灵活运用长方体的体积公式、圆锥的体积公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
