【核心考点集训】第四单元《分数的意义和性质》课件(共30张PPT)--人教版五年级下册数学
文档属性
| 名称 | 【核心考点集训】第四单元《分数的意义和性质》课件(共30张PPT)--人教版五年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 18:24:03 | ||
图片预览











文档简介
(共30张PPT)
人教版 数学 五年级 下册
分数的意义和性质
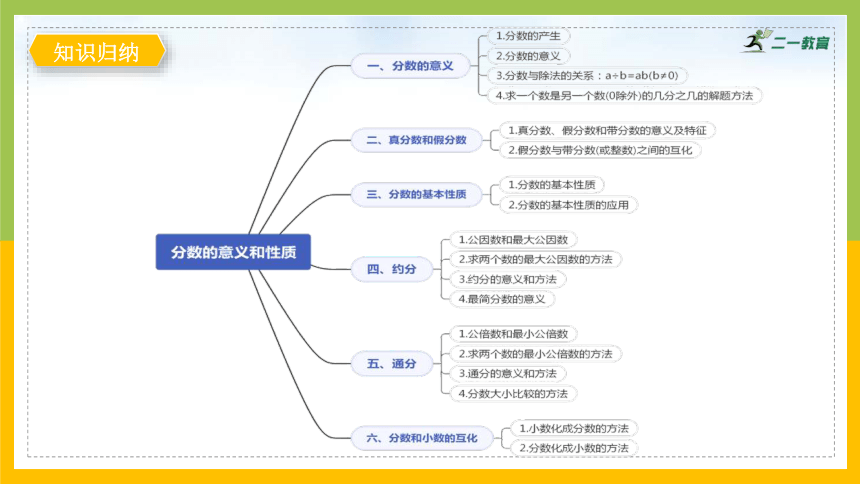
知识归纳
模块一:知识点复习
知识点一:分数的意义
知识梳理
1.一个物体、一个计量单位或是一些物体等都可以看作一个整体。一个整体可以用自然数1来表示,我们通常把它叫作单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
知识点一:分数的意义
知识梳理
1.一个物体、一个计量单位或是一些物体等都可以看作一个整体。一个整体可以用自然数1来表示,我们通常把它叫作单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
知识点二:分数与除法
知识梳理
1.两个整数相除,可以用分数表示商。反之,分数也可以看作两个数相除,分数的分子相当于被除数,分母相当于除数,分数线相当于除号。
被除数÷除数=,用字母表示为a÷b=(b≠0)。
2.求一个数是另一个数的几分之几的解题方法:
一个数÷另一个数=,即比较量÷标准量=
知识点三:真分数和假分数
知识梳理
1.分子比分母小的分数叫作真分数,真分数小于1。
2.分子大于或等于分母的分数叫作假分数,假分数大于1或等于1。
3.像2、1这样由整数(不包括0)和真分数合成的数叫作带分数,带分数大于1。
4.假分数化成整数或带分数的方法:
(1)用分子除以分母。当分子是分母的倍数时,能化成整数,商就是这个整数;
(2)当分子不是分母的倍数时,能化成带分数,商是带分数的整数部分,余数是带分数的真分数部分的分子,分母不变。
知识点四:分数的基本性质
知识梳理
1.分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫作分数的基本性质。
2.利用分数的基本性质可以把分母不同的分数化成分母相同的分数,还可以把一个分数化成指定分母的分数。
知识点五:最大公因数
知识梳理
1.几个数公有的因数叫作这几个数的公因数。其中最大的一个叫作这几个数的最大公因数。
2.求两个数的最大公因数的方法:
(1)列举法;(2)筛选法;(3)分解质因数法;(4)短除法。
3.求两个数的最大公因数的特殊情况:
(1)当两个数成倍数关系时,较小数是它们的最大公因数;
(2)当两个数的公因数只有1时,它们的最大公因数就是1。(拓展:公因数只有1的两个数,叫作互质数)
4.当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
知识点六:约分
知识梳理
1.把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。
2.约分的方法有两种:
(1)逐次约分法:用分数的分子和分母的公因数逐次去除分子和分母;
(2)一次约分法:用分数的分子和分母的最大公因数去除分子和分母。
3.分子和分母只有公因数1的分数叫作最简分数。约分时,通常要约成最简分数。
4.约分只改变分数单位的大小,分数值不变。
知识点七:最小公倍数
知识梳理
1.几个数公有的倍数,叫作它们的公倍数,其中最小的公倍数,叫作它们的最小公倍数。
2.公倍数的特征:两个数的公倍数的个数是无限的,只有最小的公倍数,没有最大的公倍数。
3.当两个数成倍数关系时,较大数就是它们的最小公倍数;当两个数只有公因数1时,这两个数的积就是它们的最小公倍数。
4.求两个数的最小公倍数的实际应用:当所求量分别与两个已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
知识点七:最小公倍数
知识梳理
5.求两个数的最小公倍数的方法:
(1)列举法:先分别找出两个数各自的倍数,再从中找出它们的公倍数,其中最小的一个就是它们的最小公倍数。
(2)筛选法:先写出两个数中较大数(或较小数)的倍数,然后从这组数中按从小到大的顺序圈出较小数(或较大数)的倍数,第一个圈出的数就是它们的最小公倍数。此外,我们还可以用分解质因数法和短除法求两个数的最小公倍数。
知识点八:通分
知识梳理
1.分母相同的两个分数相比较,分子大的分数大。分子相同的两个分数相比较,分母小的分数大。
2.把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
3.通分的方法:通分时用两个分母的公倍数作公分母(为了计算简便,通常选用最小公倍数作公分母),然后把每个分数都化成用这个公倍数作分母的分数。
4.分子、分母都不相同的分数比较大小,可以把异分母分数化成同分母分数再进行比较;如果分数的分母较大,而分子较小时,可化成分子相同的分数进行比较。
知识点九:分数和小数的互化
知识梳理
1.小数化成分数的方法:小数表示的就是十分之几、百分之几、千分之几……的数,所以可以直接写成分母是10,100,1000,…的分数,再化简。
2.分数化成小数的方法:
(1)分母是10,100,1000,…的分数化成小数,可以直接去掉分母,看分母1后面有几个0,就从分子最后一位起向左数出几位,点上小数点,位数不够时,用“0”补足,可以化成小数部分为一位、两位、三位……的小数。
(2)分母不是10,100,1000,…的分数化成小数,可以利用分数的基本性质化成分母为10,100,1000,…的分数,再化成小数;还可以利用分数与除法的关系,直接用分子除以分母。当分子除以分母除不尽时,要根据需要按“四舍五入”法取近似数。
模块二:例题讲解
【典例1】根据真、假分数的特征确定未知数的值
是假分数
是真分数
8
若是假分数(x是非零自然数),是真分数,则x=( )。
分析:
x是大于或等于8的自然数。
x是小于9的自然数。
x一定是8。
【典例2】求原带分数问题
整数=
分析:根据带分数化成假分数的方法推算:
分母是5,整数部分是2,但分数是:
一个带分数的分子是3,化成假分数后分子是13。这个带分数可能是( )。
13-3=10
3
整数×分母=10
1×10
2×5
分子是3
分母>3
分母是10,整数部分是1,但分数是:
1
1、
【典例3】约分的问题
把一个分数约分时,用2约了两次,用3约了一次,得到。原来的分数是多少
分析:方法一:用最简分数的分子和分母同时乘约分时除以的公因数,如图:
用2约分两次
用3约分一次
原分数的分子、分母同时连续两次除以2。
原分数用2约分两次后的分子、分母同时除以3。
得到
解答:
【典例3】约分的问题
分析:方法二:先求出原分数分子和分母的最大公因数,即3×2×2=12,再用最简分数的分子和分母同时乘原分数分子和分母的最大公因数。
把一个分数约分时,用2约了两次,用3约了一次,得到。原来的分数是多少
解答:3×2×2=12
【典例4】通过对比标准量比较分数大小
分析:两个分数都接近 ,可以把这两个分数先和 进行比较,再比较这两个分数的大小。
解答: =
=
所以:
【典例5】分子和分母同时加(或减)同一个数的问题
分析:首先,找出题中的不变量:约分前分数中分母与分子的差。
分子、分母同时加上一个相同的数后,它们的差不变。原分数中分母与分子的差为11-5=6,约分后的分数中分母与分子的差为2-1=1。
再根据不变量推算约分前的分数。
约分前分数的分母与分子的差是约分后分数的分母与分子的差的(6÷1)倍。根据分数的基本性质,把的分子和分母同时乘6,得到结果。
解答:(11-5)÷(2-1)=6
6-5=1(或12-11=1)
答:加上的这个数是1。
【典例6】用转化法解决有关最大公因数的实际问题
分析:46块水果糖平均分给小朋友后,剩1块。
45块水果糖正好平均分完。
把46块水果糖和38块巧克力分别平均分给几个小朋友,结果水果糖剩1块,巧克力剩3块。最多有多少个小朋友
38块巧克力平均分给小朋友后,剩3块。
35块巧克力正好平均分完。
求小朋友最多有多少个,就是求45和35的最大公因数是多少。
解答:46-1=45(块) 38-3=35(块)
45的因数有:1,3,5,9,15,45 35的因数有:1,5,7,35
所以45和35的最大公因数是5,即最多有5个小朋友。
【典例7】三个数的最大公因数的实际问题
将15cm、20cm、35cm这些木棒截成同样长的若干段,都不能有剩余,每段最长是多少厘米
分析:要把这些木棒截成同样长的若干段,不能有剩余。
求每段最长是多少,就是15,20和35的最大公因数。
截成的每段长度应是三根木棒长度(15,20和35)的公因数。
15的因数有:1 ,3,5,15
20的因数有:1 ,2,4,5,10,20
35的因数有:1 ,5,7,35
解答:15,20和35的最大公因数是5,所以每段最长是5cm。
【典例8】用综合法解决最小公倍数的应用问题
某市道路一旁共挂了125个灯笼(首尾都有)。原来每两个灯笼之间的距离是3m,现在改为4m,如果起点那个灯笼不移动,还有多少个灯笼不用移动
分析:(个数-1)×原间隔距离=总距离
不用移动的两个灯笼之间的距离,就是3和4的最小公倍数。
起点的那个灯笼不用移动。
总距离÷不用移动的两个灯笼之间的距离=除起点外不用移动的灯笼的个数
解答:(125-1)×3=372(m)
3和4的最小公倍数是12
372÷12=31(个)
【典例9】运用最大公因数解决植树类问题
分析:求出720和640的最大公因数,即相邻两益路灯之间的最大距离。
运用两端都栽的植树问题的求法:
盏数=路长÷每个间隔的距离+1。
为了迎接省运会,要在某大道的一边等距离安装路灯,而且要在A,B,C三个点上各安装一盏路灯,如图所示,则相邻两盏路灯之间的最大距离是多少米 此时需要安装多少盏路灯
求出一共需要安装的盏数
解答:720和640的最大公因数是80
(720+640)÷80+1=18(盏)
模块三:完成变式训练
2.一个带分数,它的分数部分的分子是2,把它化成假分数后,分子是27。这个带分数可能是( )。
3
或5
解答: =
= <
所以:
解答:(35-23)÷(5-3)=6
35-30=5(或23-18=5)
6.把33支钢笔和38本笔记本平均分给一些学习成绩优秀的学生,结果钢笔多出1支,笔记本还缺2本。求最多有多少名成绩优秀的学生。
33-1=32(支) 38+2=40(本)
32的因数有:1,2,4,8,16,32
40的因数有:1,2,4,5,8,10,20,40
所以32和40的最大公因数是8,即最多有8名成绩优秀的学生。
7.有三根橡胶管,长分别是24 dm、36 dm、72 dm,要把这三根橡胶管剪成同样长的小段,且三根橡胶管都没有剩余。每小段最长是多少分米 一共可以剪成多少段
解答:24,36和72的最大公因数是12,所以每小段最长是12 dm。
24÷12+36÷12+72÷12=11(段)
答:每小段最长是12 dm,可以剪成11段。
8.学校附近的一条通道一侧从头到尾有116棵树(两头都栽),原来每相邻两棵树之间的距离是9m,现在要改成每相邻两棵树之间的距离是15m,有多少棵树不需要移动
解答:9和15的最小公倍数是45
9×(116-1)÷45+1=24(棵)
答:有24棵树不需要移动。
人教版 数学 五年级 下册
分数的意义和性质
知识归纳
模块一:知识点复习
知识点一:分数的意义
知识梳理
1.一个物体、一个计量单位或是一些物体等都可以看作一个整体。一个整体可以用自然数1来表示,我们通常把它叫作单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
知识点一:分数的意义
知识梳理
1.一个物体、一个计量单位或是一些物体等都可以看作一个整体。一个整体可以用自然数1来表示,我们通常把它叫作单位“1”。
2.把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位。一个分数的分母是几,它的分数单位就是几分之一;分子是几,它就有几个这样的分数单位。
知识点二:分数与除法
知识梳理
1.两个整数相除,可以用分数表示商。反之,分数也可以看作两个数相除,分数的分子相当于被除数,分母相当于除数,分数线相当于除号。
被除数÷除数=,用字母表示为a÷b=(b≠0)。
2.求一个数是另一个数的几分之几的解题方法:
一个数÷另一个数=,即比较量÷标准量=
知识点三:真分数和假分数
知识梳理
1.分子比分母小的分数叫作真分数,真分数小于1。
2.分子大于或等于分母的分数叫作假分数,假分数大于1或等于1。
3.像2、1这样由整数(不包括0)和真分数合成的数叫作带分数,带分数大于1。
4.假分数化成整数或带分数的方法:
(1)用分子除以分母。当分子是分母的倍数时,能化成整数,商就是这个整数;
(2)当分子不是分母的倍数时,能化成带分数,商是带分数的整数部分,余数是带分数的真分数部分的分子,分母不变。
知识点四:分数的基本性质
知识梳理
1.分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫作分数的基本性质。
2.利用分数的基本性质可以把分母不同的分数化成分母相同的分数,还可以把一个分数化成指定分母的分数。
知识点五:最大公因数
知识梳理
1.几个数公有的因数叫作这几个数的公因数。其中最大的一个叫作这几个数的最大公因数。
2.求两个数的最大公因数的方法:
(1)列举法;(2)筛选法;(3)分解质因数法;(4)短除法。
3.求两个数的最大公因数的特殊情况:
(1)当两个数成倍数关系时,较小数是它们的最大公因数;
(2)当两个数的公因数只有1时,它们的最大公因数就是1。(拓展:公因数只有1的两个数,叫作互质数)
4.当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
知识点六:约分
知识梳理
1.把一个分数化成和它相等,但分子和分母都比较小的分数,叫作约分。
2.约分的方法有两种:
(1)逐次约分法:用分数的分子和分母的公因数逐次去除分子和分母;
(2)一次约分法:用分数的分子和分母的最大公因数去除分子和分母。
3.分子和分母只有公因数1的分数叫作最简分数。约分时,通常要约成最简分数。
4.约分只改变分数单位的大小,分数值不变。
知识点七:最小公倍数
知识梳理
1.几个数公有的倍数,叫作它们的公倍数,其中最小的公倍数,叫作它们的最小公倍数。
2.公倍数的特征:两个数的公倍数的个数是无限的,只有最小的公倍数,没有最大的公倍数。
3.当两个数成倍数关系时,较大数就是它们的最小公倍数;当两个数只有公因数1时,这两个数的积就是它们的最小公倍数。
4.求两个数的最小公倍数的实际应用:当所求量分别与两个已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
知识点七:最小公倍数
知识梳理
5.求两个数的最小公倍数的方法:
(1)列举法:先分别找出两个数各自的倍数,再从中找出它们的公倍数,其中最小的一个就是它们的最小公倍数。
(2)筛选法:先写出两个数中较大数(或较小数)的倍数,然后从这组数中按从小到大的顺序圈出较小数(或较大数)的倍数,第一个圈出的数就是它们的最小公倍数。此外,我们还可以用分解质因数法和短除法求两个数的最小公倍数。
知识点八:通分
知识梳理
1.分母相同的两个分数相比较,分子大的分数大。分子相同的两个分数相比较,分母小的分数大。
2.把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
3.通分的方法:通分时用两个分母的公倍数作公分母(为了计算简便,通常选用最小公倍数作公分母),然后把每个分数都化成用这个公倍数作分母的分数。
4.分子、分母都不相同的分数比较大小,可以把异分母分数化成同分母分数再进行比较;如果分数的分母较大,而分子较小时,可化成分子相同的分数进行比较。
知识点九:分数和小数的互化
知识梳理
1.小数化成分数的方法:小数表示的就是十分之几、百分之几、千分之几……的数,所以可以直接写成分母是10,100,1000,…的分数,再化简。
2.分数化成小数的方法:
(1)分母是10,100,1000,…的分数化成小数,可以直接去掉分母,看分母1后面有几个0,就从分子最后一位起向左数出几位,点上小数点,位数不够时,用“0”补足,可以化成小数部分为一位、两位、三位……的小数。
(2)分母不是10,100,1000,…的分数化成小数,可以利用分数的基本性质化成分母为10,100,1000,…的分数,再化成小数;还可以利用分数与除法的关系,直接用分子除以分母。当分子除以分母除不尽时,要根据需要按“四舍五入”法取近似数。
模块二:例题讲解
【典例1】根据真、假分数的特征确定未知数的值
是假分数
是真分数
8
若是假分数(x是非零自然数),是真分数,则x=( )。
分析:
x是大于或等于8的自然数。
x是小于9的自然数。
x一定是8。
【典例2】求原带分数问题
整数=
分析:根据带分数化成假分数的方法推算:
分母是5,整数部分是2,但分数是:
一个带分数的分子是3,化成假分数后分子是13。这个带分数可能是( )。
13-3=10
3
整数×分母=10
1×10
2×5
分子是3
分母>3
分母是10,整数部分是1,但分数是:
1
1、
【典例3】约分的问题
把一个分数约分时,用2约了两次,用3约了一次,得到。原来的分数是多少
分析:方法一:用最简分数的分子和分母同时乘约分时除以的公因数,如图:
用2约分两次
用3约分一次
原分数的分子、分母同时连续两次除以2。
原分数用2约分两次后的分子、分母同时除以3。
得到
解答:
【典例3】约分的问题
分析:方法二:先求出原分数分子和分母的最大公因数,即3×2×2=12,再用最简分数的分子和分母同时乘原分数分子和分母的最大公因数。
把一个分数约分时,用2约了两次,用3约了一次,得到。原来的分数是多少
解答:3×2×2=12
【典例4】通过对比标准量比较分数大小
分析:两个分数都接近 ,可以把这两个分数先和 进行比较,再比较这两个分数的大小。
解答: =
=
所以:
【典例5】分子和分母同时加(或减)同一个数的问题
分析:首先,找出题中的不变量:约分前分数中分母与分子的差。
分子、分母同时加上一个相同的数后,它们的差不变。原分数中分母与分子的差为11-5=6,约分后的分数中分母与分子的差为2-1=1。
再根据不变量推算约分前的分数。
约分前分数的分母与分子的差是约分后分数的分母与分子的差的(6÷1)倍。根据分数的基本性质,把的分子和分母同时乘6,得到结果。
解答:(11-5)÷(2-1)=6
6-5=1(或12-11=1)
答:加上的这个数是1。
【典例6】用转化法解决有关最大公因数的实际问题
分析:46块水果糖平均分给小朋友后,剩1块。
45块水果糖正好平均分完。
把46块水果糖和38块巧克力分别平均分给几个小朋友,结果水果糖剩1块,巧克力剩3块。最多有多少个小朋友
38块巧克力平均分给小朋友后,剩3块。
35块巧克力正好平均分完。
求小朋友最多有多少个,就是求45和35的最大公因数是多少。
解答:46-1=45(块) 38-3=35(块)
45的因数有:1,3,5,9,15,45 35的因数有:1,5,7,35
所以45和35的最大公因数是5,即最多有5个小朋友。
【典例7】三个数的最大公因数的实际问题
将15cm、20cm、35cm这些木棒截成同样长的若干段,都不能有剩余,每段最长是多少厘米
分析:要把这些木棒截成同样长的若干段,不能有剩余。
求每段最长是多少,就是15,20和35的最大公因数。
截成的每段长度应是三根木棒长度(15,20和35)的公因数。
15的因数有:1 ,3,5,15
20的因数有:1 ,2,4,5,10,20
35的因数有:1 ,5,7,35
解答:15,20和35的最大公因数是5,所以每段最长是5cm。
【典例8】用综合法解决最小公倍数的应用问题
某市道路一旁共挂了125个灯笼(首尾都有)。原来每两个灯笼之间的距离是3m,现在改为4m,如果起点那个灯笼不移动,还有多少个灯笼不用移动
分析:(个数-1)×原间隔距离=总距离
不用移动的两个灯笼之间的距离,就是3和4的最小公倍数。
起点的那个灯笼不用移动。
总距离÷不用移动的两个灯笼之间的距离=除起点外不用移动的灯笼的个数
解答:(125-1)×3=372(m)
3和4的最小公倍数是12
372÷12=31(个)
【典例9】运用最大公因数解决植树类问题
分析:求出720和640的最大公因数,即相邻两益路灯之间的最大距离。
运用两端都栽的植树问题的求法:
盏数=路长÷每个间隔的距离+1。
为了迎接省运会,要在某大道的一边等距离安装路灯,而且要在A,B,C三个点上各安装一盏路灯,如图所示,则相邻两盏路灯之间的最大距离是多少米 此时需要安装多少盏路灯
求出一共需要安装的盏数
解答:720和640的最大公因数是80
(720+640)÷80+1=18(盏)
模块三:完成变式训练
2.一个带分数,它的分数部分的分子是2,把它化成假分数后,分子是27。这个带分数可能是( )。
3
或5
解答: =
= <
所以:
解答:(35-23)÷(5-3)=6
35-30=5(或23-18=5)
6.把33支钢笔和38本笔记本平均分给一些学习成绩优秀的学生,结果钢笔多出1支,笔记本还缺2本。求最多有多少名成绩优秀的学生。
33-1=32(支) 38+2=40(本)
32的因数有:1,2,4,8,16,32
40的因数有:1,2,4,5,8,10,20,40
所以32和40的最大公因数是8,即最多有8名成绩优秀的学生。
7.有三根橡胶管,长分别是24 dm、36 dm、72 dm,要把这三根橡胶管剪成同样长的小段,且三根橡胶管都没有剩余。每小段最长是多少分米 一共可以剪成多少段
解答:24,36和72的最大公因数是12,所以每小段最长是12 dm。
24÷12+36÷12+72÷12=11(段)
答:每小段最长是12 dm,可以剪成11段。
8.学校附近的一条通道一侧从头到尾有116棵树(两头都栽),原来每相邻两棵树之间的距离是9m,现在要改成每相邻两棵树之间的距离是15m,有多少棵树不需要移动
解答:9和15的最小公倍数是45
9×(116-1)÷45+1=24(棵)
答:有24棵树不需要移动。
