11.2一元一次不等式的概念 课件(共17张PPT) 苏科版(2024)数学七年级下册
文档属性
| 名称 | 11.2一元一次不等式的概念 课件(共17张PPT) 苏科版(2024)数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 983.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
一元一次不等式的概念
学习目标
了解一元一次不等式的概念,不等式的解与解集的概念
2.会在数轴上表示不等式的解集,感受数形结合的思想,发展几何直观.
情景导入1
举例说明什么是不等式?
例如:x+20<50,a≦80,t 9,0.5x+70≦100,
具有上面这些特点的不等式,你能给他们起一个符合这些特征名字吗?
不等式x+20<50,a≦80,t 9,0.5x+70≦100有什么共同特征?
共同点:
1.它们都只含有一个未知数,
2.并且未知数的最高次数是1
3.两边都是是整式
一元一次不等式
一元一次不等式概念:只含有一个未知数,并且未知数的次数是1的不等式叫一元一次不等式,例如 : 1+x<4.0
新知学习
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式; (2)只含有一个未知数;
(3)未知数的次数为1.
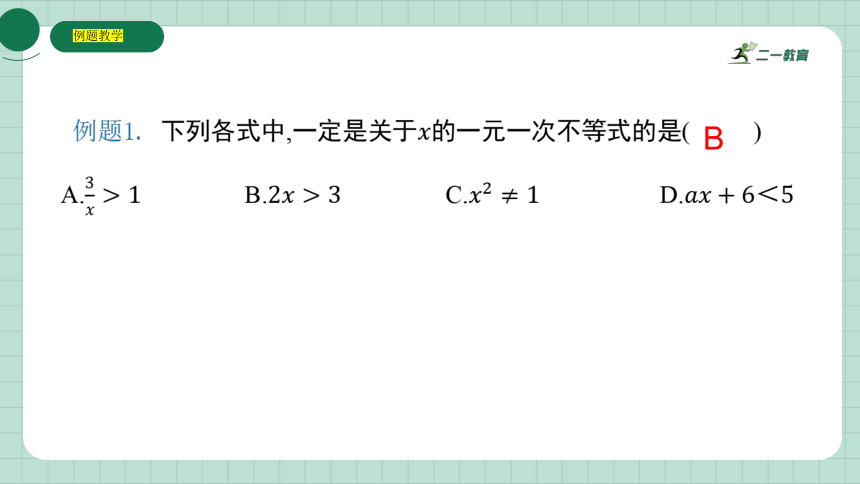
例题1. 下列各式中,一定是关于 的一元一次不等式的是( )
A. B. C. D.
例题教学
B
情景导入2
复习:什么是方程的解?
能使方程左右两边相等的未知数的值就是方程的解
例如:判断:x=3是方程1+x=4.0的解吗?
解:是的,理由如下:
当x=3时,左边=1+3=4.0
右边=4.0
左边=右边
∴x=3是方程1+x=4.0的解
类比方程的解:你能说一说什么是不等式的解吗?
能使不等式成立的未知数的值是不等式的解,
新知学习
2.不等式的解:
符合不等式的某个未知数的值叫不等式的解
例如:判断x=2 ,x=3.5 是不等式1+x<4的解
解:x=2 是不等式1+x<4的解,x=3.5 不是不等式1+x<4的解,理由如下:
∵2+1=3<4,∴x=2 满足不等式1+x<4
∵ 3.5+1=4.5>4,∴x=3.5不满足不等式1+x<4
∴x=2 是不等式1+x<4的解,
x=3.5 不是不等式1+x<4的解
情景导入2
思考:不等式1+x<4的解有多少个呢?这些解有什么共同特征?
进一步判断:x=1,x=2.9 是不等式1+x<4的解吗?
是的
不等式1+x<4 有无数个解,
特征: 他们都小于3
把所有的解放在一起,叫做不等式的解集
3.不等式的解集:
所有的解组成的全体叫做这个不等式的解集
例如: 1+x<4的解集是:x<3
新知学习
4.解不等式:求不等式解集的过程叫解不等式
注意点:不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中.
新知学习
不等式解集在数轴上的表示
在数轴上表示不等式的解集
不等式的解集表示未知数的取值范围,所以不等式的解集可以在数
轴上直观地表示出来.一般地,利用数轴表示不等式的解集通常有
以下四种情况(设 ):
不等式 的解集
数轴表 示 ________________________________ ________________________________ ______________________________ ________________________________
注意点:1.没有等于号的,用空心圆圈表示,
2.有等于号的,用实心圆圈表示 3.定方向,大于向右,小于向左.
例题2
1:在数轴上表示下列不等式
(1)x<-2 (2)x≦-2 (3)x>-2 (4)x≧-2
例题2
x<3
x>
x≥-2
x≤
巩固练习
1.下列式子中,属于一元一次不等式的是( )
A.x+y≥2 B.x-3<15 C.>4 D.x+2=7
B
2.如果x=2.3是某不等式的解,那么该不等式可以是( )
A.x>4 B.x<2 C.x<3 D.x>3
c
3.不等式-1≤x<3所有整数解是 .
-1,0,1,2
4.已知关于x的不等式x>a-3的解在数轴上表示如图所示,则a的值为 。
2
巩固练习
5.若一个不等式的正整数解为1和2,则该不等式的解集在数轴上的表示可能是( )
C
6.在数轴上表示下列各数
(1)x<6 (2)x≥-3 (3)x≤-1 (4)x<
素养提升
.已知x=3是不等式 (x-2)(ax+1)>0的解,且x=-1不是该不等式的解,则a的值可以是( )
A.-1 B .-2 C.0.5 D.2
解:∵x=3是该不等式的解
∴(3-2)(3a+1)>0
∴a> -
∵x=-1不是该不等式的解
∴(-1-2)(-a+1)≤0
∴ a≤1
∴ - < a≤1
C
总结提升
通过这节课的学习,你有哪些收获呢?
1.一元一次不等式的概念
2.不能式的解和不等式的解集
3.不等式的解集在数轴上的表示
再见
一元一次不等式的概念
学习目标
了解一元一次不等式的概念,不等式的解与解集的概念
2.会在数轴上表示不等式的解集,感受数形结合的思想,发展几何直观.
情景导入1
举例说明什么是不等式?
例如:x+20<50,a≦80,t 9,0.5x+70≦100,
具有上面这些特点的不等式,你能给他们起一个符合这些特征名字吗?
不等式x+20<50,a≦80,t 9,0.5x+70≦100有什么共同特征?
共同点:
1.它们都只含有一个未知数,
2.并且未知数的最高次数是1
3.两边都是是整式
一元一次不等式
一元一次不等式概念:只含有一个未知数,并且未知数的次数是1的不等式叫一元一次不等式,例如 : 1+x<4.0
新知学习
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式; (2)只含有一个未知数;
(3)未知数的次数为1.
例题1. 下列各式中,一定是关于 的一元一次不等式的是( )
A. B. C. D.
例题教学
B
情景导入2
复习:什么是方程的解?
能使方程左右两边相等的未知数的值就是方程的解
例如:判断:x=3是方程1+x=4.0的解吗?
解:是的,理由如下:
当x=3时,左边=1+3=4.0
右边=4.0
左边=右边
∴x=3是方程1+x=4.0的解
类比方程的解:你能说一说什么是不等式的解吗?
能使不等式成立的未知数的值是不等式的解,
新知学习
2.不等式的解:
符合不等式的某个未知数的值叫不等式的解
例如:判断x=2 ,x=3.5 是不等式1+x<4的解
解:x=2 是不等式1+x<4的解,x=3.5 不是不等式1+x<4的解,理由如下:
∵2+1=3<4,∴x=2 满足不等式1+x<4
∵ 3.5+1=4.5>4,∴x=3.5不满足不等式1+x<4
∴x=2 是不等式1+x<4的解,
x=3.5 不是不等式1+x<4的解
情景导入2
思考:不等式1+x<4的解有多少个呢?这些解有什么共同特征?
进一步判断:x=1,x=2.9 是不等式1+x<4的解吗?
是的
不等式1+x<4 有无数个解,
特征: 他们都小于3
把所有的解放在一起,叫做不等式的解集
3.不等式的解集:
所有的解组成的全体叫做这个不等式的解集
例如: 1+x<4的解集是:x<3
新知学习
4.解不等式:求不等式解集的过程叫解不等式
注意点:不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中.
新知学习
不等式解集在数轴上的表示
在数轴上表示不等式的解集
不等式的解集表示未知数的取值范围,所以不等式的解集可以在数
轴上直观地表示出来.一般地,利用数轴表示不等式的解集通常有
以下四种情况(设 ):
不等式 的解集
数轴表 示 ________________________________ ________________________________ ______________________________ ________________________________
注意点:1.没有等于号的,用空心圆圈表示,
2.有等于号的,用实心圆圈表示 3.定方向,大于向右,小于向左.
例题2
1:在数轴上表示下列不等式
(1)x<-2 (2)x≦-2 (3)x>-2 (4)x≧-2
例题2
x<3
x>
x≥-2
x≤
巩固练习
1.下列式子中,属于一元一次不等式的是( )
A.x+y≥2 B.x-3<15 C.>4 D.x+2=7
B
2.如果x=2.3是某不等式的解,那么该不等式可以是( )
A.x>4 B.x<2 C.x<3 D.x>3
c
3.不等式-1≤x<3所有整数解是 .
-1,0,1,2
4.已知关于x的不等式x>a-3的解在数轴上表示如图所示,则a的值为 。
2
巩固练习
5.若一个不等式的正整数解为1和2,则该不等式的解集在数轴上的表示可能是( )
C
6.在数轴上表示下列各数
(1)x<6 (2)x≥-3 (3)x≤-1 (4)x<
素养提升
.已知x=3是不等式 (x-2)(ax+1)>0的解,且x=-1不是该不等式的解,则a的值可以是( )
A.-1 B .-2 C.0.5 D.2
解:∵x=3是该不等式的解
∴(3-2)(3a+1)>0
∴a> -
∵x=-1不是该不等式的解
∴(-1-2)(-a+1)≤0
∴ a≤1
∴ - < a≤1
C
总结提升
通过这节课的学习,你有哪些收获呢?
1.一元一次不等式的概念
2.不能式的解和不等式的解集
3.不等式的解集在数轴上的表示
再见
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
